|
Hyperbolic Space
In mathematics, hyperbolic space of dimension n is the unique simply connected, n-dimensional Riemannian manifold of constant sectional curvature equal to -1. It is homogeneous, and satisfies the stronger property of being a symmetric space. There are many ways to construct it as an open subset of \mathbb R^n with an explicitly written Riemannian metric; such constructions are referred to as models. Hyperbolic 2-space, H2, which was the first instance studied, is also called the hyperbolic plane. It is also sometimes referred to as Lobachevsky space or Bolyai–Lobachevsky space after the names of the author who first published on the topic of hyperbolic geometry. Sometimes the qualificative "real" is added to differentiate it from complex hyperbolic spaces, quaternionic hyperbolic spaces and the octononic hyperbolic plane which are the other symmetric spaces of negative curvature. Hyperbolic space serves as the prototype of a Gromov hyperbolic space which is a far-reac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Orthogonal Dodecahedral Honeycomb
Hyperbolic is an adjective describing something that resembles or pertains to a hyperbola (a curve), to hyperbole (an overstatement or exaggeration), or to hyperbolic geometry. The following phenomena are described as ''hyperbolic'' because they manifest hyperbolas, not because something about them is exaggerated. * Hyperbolic angle, an unbounded variable referring to a hyperbola instead of a circle * Hyperbolic coordinates, location by geometric mean and hyperbolic angle in quadrant I * Hyperbolic distribution, a probability distribution characterized by the logarithm of the probability density function being a hyperbola * Hyperbolic equilibrium point, a fixed point that does not have any center manifolds * Hyperbolic function, an analog of an ordinary trigonometric or circular function * Hyperbolic geometric graph, a random network generated by connecting nearby points sprinkled in a hyperbolic space * Hyperbolic geometry, a non-Euclidean geometry * Hyperbolic group, a finite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
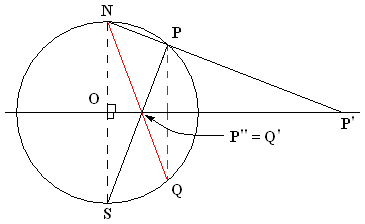
Poincaré Disc Model
Poincaré is a French surname. Notable people with the surname include: * Henri Poincaré (1854–1912), French physicist, mathematician and philosopher of science * Henriette Poincaré (1858-1943), wife of Prime Minister Raymond Poincaré * Lucien Poincaré (1862–1920), physicist, brother of Raymond and cousin of Henri * Raymond Poincaré (1860–1934), French Prime Minister or President ''inter alia'' from 1913 to 1920, cousin of Henri See also *List of things named after Henri Poincaré In physics and mathematics, a number of ideas are named after Henri Poincaré: * Euler–Poincaré characteristic * Hilbert–Poincaré series * Poincaré–Bendixson theorem * Poincaré–Birkhoff theorem * Poincaré–Birkhoff–Witt theorem, us .... * * {{DEFAULTSORT:Poincare French-language surnames ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of '' proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as evident (for example, there is exactly one straight line passing through two points), or seemed impossible to prove (paral ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gauß ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes referred to as the ''Princeps mathematicorum'' () and "the greatest mathematician since antiquity", Gauss had an exceptional influence in many fields of mathematics and science, and he is ranked among history's most influential mathematicians. Also available at Retrieved 23 February 2014. Comprehensive biographical article. Biography Early years Johann Carl Friedrich Gauss was born on 30 April 1777 in Brunswick (Braunschweig), in the Duchy of Brunswick-Wolfenbüttel (now part of Lower Saxony, Germany), to poor, working-class parents. His mother was illiterate and never recorded the date of his birth, remembering only that he had been born on a Wednesday, eight days before the Feast of the Ascension (which occurs 39 days after Easter). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
János Bolyai
János Bolyai (; 15 December 1802 – 27 January 1860) or Johann Bolyai, was a Hungarian mathematician, who developed absolute geometry—a geometry that includes both Euclidean geometry and hyperbolic geometry. The discovery of a consistent alternative geometry that might correspond to the structure of the universe helped to free mathematicians to study abstract concepts irrespective of any possible connection with the physical world. Early life Bolyai was born in the Hungarian town of Kolozsvár, Grand Principality of Transylvania (now Cluj-Napoca in Romania), the son of Zsuzsanna Benkő and the well-known mathematician Farkas Bolyai. By the age of 13, he had mastered calculus and other forms of analytical mechanics, receiving instruction from his father. He studied at the Imperial and Royal Military Academy (TherMilAk) in Vienna from 1818 to 1822. Career Bolyai became so obsessed with Euclid's parallel postulate that his father, who had pursued the same subje ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nikolai Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, Никола́й Ива́нович Лобаче́вский, p=nʲikɐˈlaj ɪˈvanəvʲɪtɕ ləbɐˈtɕɛfskʲɪj, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; – ) was a Russian mathematician and geometer, known primarily for his work on hyperbolic geometry, otherwise known as Lobachevskian geometry, and also for his fundamental study on Dirichlet integrals, known as the Lobachevsky integral formula. William Kingdon Clifford called Lobachevsky the "Copernicus of Geometry" due to the revolutionary character of his work. Biography Nikolai Lobachevsky was born either in or near the city of Nizhny Novgorod in the Russian Empire (now in Nizhny Novgorod Oblast, Russia) in 1792 to parents of Russian and Polish origin – Ivan Maksimovich Lobachevsky and Praskovia Alexandrovna Lobachevskaya.Victor J. Katz. ''A history of mathematics: Introduction''. Addison-Wesley. 2009. p. 842. Stephen Hawking. ''God Created the Integers: The Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coset Space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group ''G'' is a non-empty manifold or topological space ''X'' on which ''G'' acts transitively. The elements of ''G'' are called the symmetries of ''X''. A special case of this is when the group ''G'' in question is the automorphism group of the space ''X'' – here "automorphism group" can mean isometry group, diffeomorphism group, or homeomorphism group. In this case, ''X'' is homogeneous if intuitively ''X'' looks locally the same at each point, either in the sense of isometry (rigid geometry), diffeomorphism (differential geometry), or homeomorphism (topology). Some authors insist that the action of ''G'' be faithful (non-identity elements act non-trivially), although the present article does not. Thus there is a group action of ''G'' on ''X'' which can be thought of as preserving some "geometric structure" on ''X'', and making ''X'' into a single ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Klein Model
Klein may refer to: People *Klein (surname) * Klein (musician) Places * Klein (crater), a lunar feature * Klein, Montana, United States *Klein, Texas, United States * Klein (Ohm), a river of Hesse, Germany, tributary of the Ohm *Klein River, a river in the Western Cape province of South Africa Business * Klein Bikes, a bicycle manufacturer * Klein Tools, a manufacturer * S. Klein, a department store * Klein Modellbahn, an Austrian model railway manufacturer Arts * Klein + M.B.O., an Italian musical group *Klein Award, for comic art *Yves Klein, French artist Mathematics *Klein bottle, an unusual shape in topology *Klein geometry * Klein configuration, in geometry * Klein cubic (other) * Klein graphs, in graph theory * Klein model, or Beltrami–Klein model, a model of hyperbolic geometry *Klein polyhedron, a generalization of continued fractions to higher dimensions, in the geometry of numbers *Klein surface, a dianalytic manifold of complex dimension 1 Other uses * K ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Space
In mathematics, the concept of a projective space originated from the visual effect of perspective, where parallel lines seem to meet ''at infinity''. A projective space may thus be viewed as the extension of a Euclidean space, or, more generally, an affine space with points at infinity, in such a way that there is one point at infinity of each direction of parallel lines. This definition of a projective space has the disadvantage of not being isotropic, having two different sorts of points, which must be considered separately in proofs. Therefore, other definitions are generally preferred. There are two classes of definitions. In synthetic geometry, ''point'' and ''line'' are primitive entities that are related by the incidence relation "a point is on a line" or "a line passes through a point", which is subject to the axioms of projective geometry. For some such set of axioms, the projective spaces that are defined have been shown to be equivalent to those resulting from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stereographic Projection
In mathematics, a stereographic projection is a perspective projection of the sphere, through a specific point on the sphere (the ''pole'' or ''center of projection''), onto a plane (the ''projection plane'') perpendicular to the diameter through the point. It is a smooth, bijective function from the entire sphere except the center of projection to the entire plane. It maps circles on the sphere to circles or lines on the plane, and is conformal, meaning that it preserves angles at which curves meet and thus locally approximately preserves shapes. It is neither isometric (distance preserving) nor equiareal (area preserving). The stereographic projection gives a way to represent a sphere by a plane. The metric induced by the inverse stereographic projection from the plane to the sphere defines a geodesic distance between points in the plane equal to the spherical distance between the spherical points they represent. A two-dimensional coordinate system on the stere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
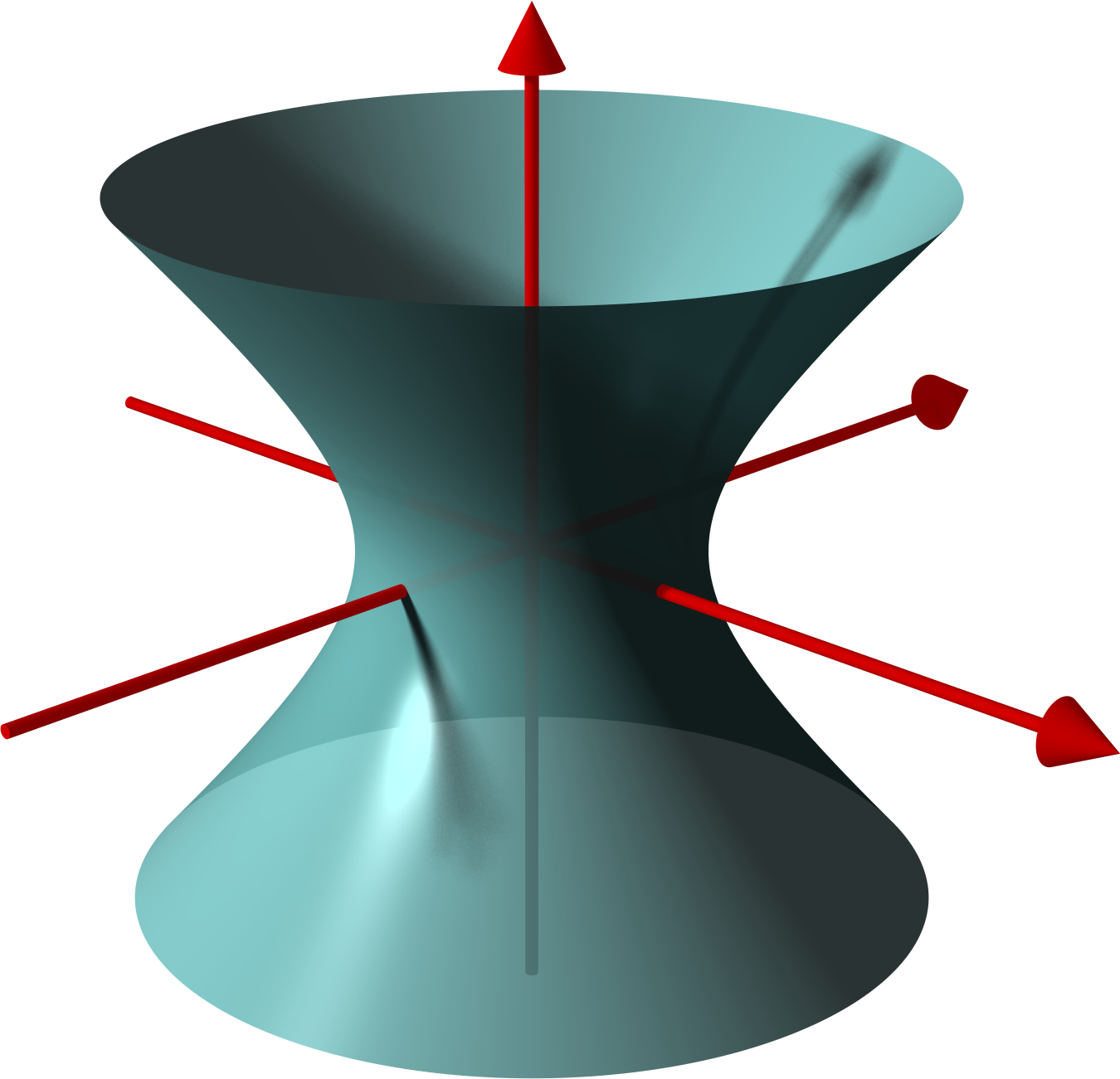
Hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by deforming it by means of directional scalings, or more generally, of an affine transformation. A hyperboloid is a quadric surface, that is, a surface defined as the zero set of a polynomial of degree two in three variables. Among quadric surfaces, a hyperboloid is characterized by not being a cone or a cylinder, having a center of symmetry, and intersecting many planes into hyperbolas. A hyperboloid has three pairwise perpendicular axes of symmetry, and three pairwise perpendicular planes of symmetry. Given a hyperboloid, one can choose a Cartesian coordinate system such that the hyperboloid is defined by one of the following equations: : + - = 1, or : + - = -1. The coordinate axes are axes of symmetry of the hyperboloid and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lorentzian Manifold
In differential geometry, a pseudo-Riemannian manifold, also called a semi-Riemannian manifold, is a differentiable manifold with a metric tensor that is everywhere nondegenerate. This is a generalization of a Riemannian manifold in which the requirement of positive-definiteness is relaxed. Every tangent space of a pseudo-Riemannian manifold is a pseudo-Euclidean vector space. A special case used in general relativity is a four-dimensional Lorentzian manifold for modeling spacetime, where tangent vectors can be classified as timelike, null, and spacelike. Introduction Manifolds In differential geometry, a differentiable manifold is a space which is locally similar to a Euclidean space. In an ''n''-dimensional Euclidean space any point can be specified by ''n'' real numbers. These are called the coordinates of the point. An ''n''-dimensional differentiable manifold is a generalisation of ''n''-dimensional Euclidean space. In a manifold it may only be possible t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |