Gram–Schmidt process

In mathematics, particularly linear algebra and numerical analysis, the Gram–Schmidt process is a method for orthonormalizing a set of vectors in an inner product space, most commonly the Euclidean space equipped with the standard inner product. The Gram–Schmidt process takes a finite, linearly independent set of vectors for and generates an orthogonal set that spans the same ''k''-dimensional subspace of R^''n'' as ''S''.

The method is named after Jørgen Pedersen Gram and Erhard Schmidt, but Pierre-Simon Laplace had been familiar with it before Gram and Schmidt. In the theory of Lie group decompositions it is generalized by the Iwasawa decomposition.

The application of the Gram–Schmidt process to the column vectors of a full column rank matrix yields the QR decomposition (it is decomposed into an orthogonal and a triangular matrix).

The Gram–Schmidt process

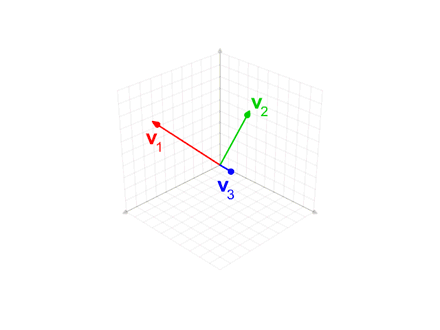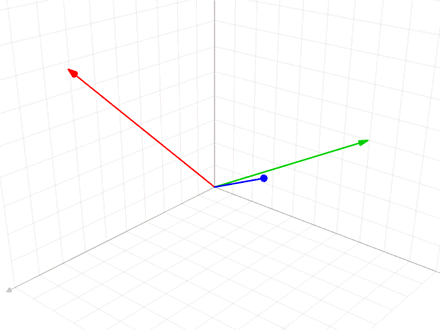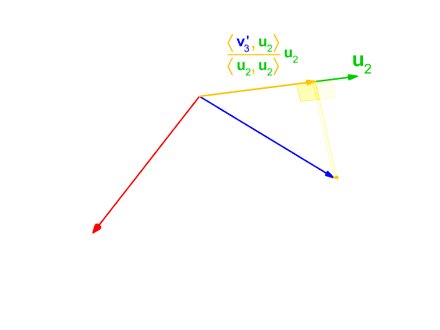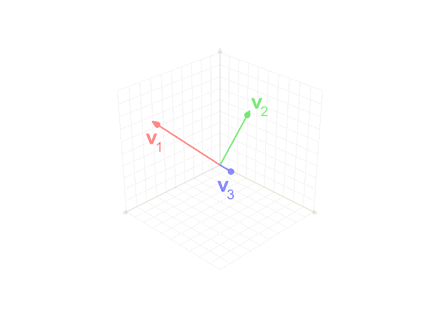
We define the projection operator by
$\operatorname_ (\mathbf) = \frac ,$

where $\langle \mathbf, \mathbf\rangle$ denotes the inner product of the vectors u and v. This operator projects the vector v orthogonally onto the line spanned by vector u. If u = 0, we define $\operatorname_\mathbf (\mathbf) := \mathbf$, i.e., the projection map $\operatorname_\mathbf$ is the zero map, sending every vector to the zero vector.

The Gram–Schmidt process then works as follows:
$\begin \mathbf_1 & = \mathbf_1, & \mathbf_1 & = \frac \\ \mathbf_2 & = \mathbf_2-\operatorname_ (\mathbf_2), & \mathbf_2 & = \frac \\ \mathbf_3 & = \mathbf_3-\operatorname_ (\mathbf_3) - \operatorname_ (\mathbf_3), & \mathbf_3 & = \frac \\ \mathbf_4 & = \mathbf_4-\operatorname_ (\mathbf_4)-\operatorname_ (\mathbf_4)-\operatorname_ (\mathbf_4), & \mathbf_4 & = \\ & \ \ \vdots & & \ \ \vdots \\ \mathbf_k & = \mathbf_k - \sum_^\operatorname_ (\mathbf_k), & \mathbf_k & = \frac. \end$

The sequence is the required system of orthogonal vectors, and the normalized vectors form an ortho''normal'' set. The calculation of the sequence is known as ''Gram–Schmidt orthogonalization'', while the calculation of the sequence is known as ''Gram–Schmidt orthonormalization'' as the vectors are normalized.

To check that these formulas yield an orthogonal sequence, first compute $\langle \mathbf_1, \mathbf_2 \rangle$ by substituting the above formula for u₂: we get zero. Then use this to compute $\langle \mathbf_1, \mathbf_3 \rangle$ again by substituting the formula for u₃: we get zero. The general proof proceeds by mathematical induction.

Geometrically, this method proceeds as follows: to compute u_''i'', it projects v_''i'' orthogonally onto the subspace ''U'' generated by , which is the same as the subspace generated by . The vector u_''i'' is then defined to be the difference between v_''i'' and this projection, guaranteed to be orthogonal to all of the vectors in the subspace ''U''.

The Gram–Schmidt process also applies to a linearly independent countably infinite sequence . The result is an orthogonal (or orthonormal) sequence such that for natural number :
the algebraic span of is the same as that of .

If the Gram–Schmidt process is applied to a linearly dependent sequence, it outputs the vector on the ''i''th step, assuming that is a linear combination of . If an orthonormal basis is to be produced, then the algorithm should test for zero vectors in the output and discard them because no multiple of a zero vector can have a length of 1. The number of vectors output by the algorithm will then be the dimension of the space spanned by the original inputs.

A variant of the Gram–Schmidt process using transfinite recursion applied to a (possibly uncountably) infinite sequence of vectors $(v_\alpha)_$ yields a set of orthonormal vectors $(u_\alpha)_$ with $\kappa\leq\lambda$ such that for any $\alpha\leq\lambda$, the completion of the span of $\$ is the same as that of In particular, when applied to a (algebraic) basis of a Hilbert space (or, more generally, a basis of any dense subspace), it yields a (functional-analytic) orthonormal basis. Note that in the general case often the strict inequality $\kappa < \lambda$ holds, even if the starting set was linearly independent, and the span of $(u_\alpha)_$ need not be a subspace of the span of $(v_\alpha)_$ (rather, it's a subspace of its completion).

Example

Euclidean space

Consider the following set of vectors in (with the conventional inner product)
$S = \left\.$

Now, perform Gram–Schmidt, to obtain an orthogonal set of vectors:
$\mathbf_1=\mathbf_1=\begin3\\1\end$
$\mathbf_2 = \mathbf_2 - \operatorname_ (\mathbf_2) = \begin2\\2\end - \operatorname_ = \begin2\\2\end - \frac \begin 3 \\1 \end = \begin -2/5 \\6/5 \end.$

We check that the vectors and are indeed orthogonal:
$\langle\mathbf_1,\mathbf_2\rangle = \left\langle \begin3\\1\end, \begin -2/5 \\ 6/5 \end \right\rangle = -\frac + \frac = 0,$
noting that if the dot product of two vectors is 0 then they are orthogonal.

For non-zero vectors, we can then normalize the vectors by dividing out their sizes as shown above:
$\mathbf_1 = \frac\begin3\\1\end$
$\mathbf_2 = \frac \begin-2/5\\6/5\end = \frac \begin-1\\3\end.$

Properties

Denote by $\operatorname(\mathbf_1, \dots, \mathbf_k)$ the result of applying the Gram–Schmidt process to a collection of vectors $\mathbf_1, \dots, \mathbf_k$. This yields a map $\operatorname \colon (\R^n)^ \to (\R^n)^$.

It has the following properties:

* It is continuous
* It is orientation preserving in the sense that $\operatorname(\mathbf_1,\dots,\mathbf_k) = \operatorname(\operatorname(\mathbf_1,\dots,\mathbf_k))$.
* It commutes with orthogonal maps:

Let $g \colon \R^n \to \R^n$ be orthogonal (with respect to the given inner product). Then we have
$\operatorname(g(\mathbf_1),\dots,g(\mathbf_k)) = \left( g(\operatorname(\mathbf_1,\dots,\mathbf_k)_1),\dots,g(\operatorname(\mathbf_1,\dots,\mathbf_k)_k) \right)$

Further a parametrized version of the Gram–Schmidt process yields a (strong) deformation retraction of the general linear group $\mathrm(\R^n)$ onto the orthogonal group $O(\R^n)$.

Numerical stability

When this process is implemented on a computer, the vectors $\mathbf_k$ are often not quite orthogonal, due to rounding errors. For the Gram–Schmidt process as described above (sometimes referred to as "classical Gram–Schmidt") this loss of orthogonality is particularly bad; therefore, it is said that the (classical) Gram–Schmidt process is numerically unstable.

The Gram–Schmidt process can be stabilized by a small modification; this version is sometimes referred to as modified Gram-Schmidt or MGS. This approach gives the same result as the original formula in exact arithmetic and introduces smaller errors in finite-precision arithmetic.
Instead of computing the vector as
$\mathbf_k = \mathbf_k - \operatorname_ (\mathbf_k) - \operatorname_ (\mathbf_k) - \cdots - \operatorname_ (\mathbf_k),$
it is computed as
$\begin \mathbf_k^ &= \mathbf_k - \operatorname_ (\mathbf_k), \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ & \;\; \vdots \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ \mathbf_k^ &= \mathbf_k^ - \operatorname_ \left(\mathbf_k^\right), \\ \mathbf_k &= \frac \end$

This method is used in the previous animation, when the intermediate vector is used when orthogonalizing the blue vector .

Here is another description of the modified algorithm. Given the vectors $v_1, v_2, \dots, v_n$, in our first step we produce vectors $v_1, v_2^, \dots, v_n^$by removing components along the direction of $v_1$. In formulas, $v_k^ := v_k - \fracv_1$. After this step we already have two of our desired orthogonal vectors $u_1, \dots, u_n$, namely $u_1 = v_1, u_2 = v_2^$, but we also made $v_3^, \dots, v_n^$ already orthogonal to $u_1$. Next, we orthogonalize those remaining vectors against $u_2 = v_2^$. This means we compute $v_3^, v_4^, \dots, v_n^$ by subtraction $v_k^ := v_k^ - \frac u_2$. Now we have stored the vectors $v_1, v_2^, v_3^, v_4^, \dots, v_n^$ where the first three vectors are already $u_1, u_2, u_3$ and the remaining vectors are already orthogonal to $u_1, u_2$. As should be clear now, the next step orthogonalizes $v_4^, \dots, v_n^$ against $u_3 = v_3^$. Proceeding in this manner we find the full set of orthogonal vectors $u_1, \dots, u_n$. If orthonormal vectors are desired, then we normalize as we go, so that the denominators in the subtraction formulas turn into ones.

Algorithm

The following MATLAB algorithm implements the Gram–Schmidt orthonormalization for Euclidean Vectors. The vectors (columns of matrix V, so that V(:,j) is the ''j''th vector) are replaced by orthonormal vectors (columns of U) which span the same subspace.

function gramschmidt(V)
,k= size(V);
U = zeros(n,k);
U(:,1) = V(:,1)/norm(V(:,1));
for i = 2:k
U(:,i)=V(:,i);
for j=1:i-1
U(:,i)=U(:,i)-(U(:,j)'*U(:,i)) * U(:,j);
end
U(:,i) = U(:,i)/norm(U(:,i));
end
end

The cost of this algorithm is asymptotically floating point operations, where is the dimensionality of the vectors.

Via Gaussian elimination

If the rows are written as a matrix $A$, then applying Gaussian elimination to the augmented matrix \left A \right/math> will produce the orthogonalized vectors in place of $A$. However the matrix $A A^\mathsf$ must be brought to row echelon form, using only the row operation of adding a scalar multiple of one row to another. For example, taking $\mathbf_1 = \begin 3 & 1\end, \mathbf_2=\begin2 & 2\end$ as above, we have
\left A \right= \left begin 10 & 8 & 3 & 1 \\ 8 & 8 & 2 & 2\end\right/math>

And reducing this to row echelon form produces
\left begin 1 & .8 & .3 & .1 \\ 0 & 1 & -.25 & .75\end\right/math>

The normalized vectors are then
$\mathbf_1 = \frac\begin.3 & .1\end = \frac \begin3 & 1\end$
$\mathbf_2 = \frac \begin-.25 & .75\end = \frac \begin-1 & 3\end,$
as in the example above.

Determinant formula

The result of the Gram–Schmidt process may be expressed in a non-recursive formula using determinants.

$\mathbf_j = \frac \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_ \rangle & \langle \mathbf_2, \mathbf_ \rangle & \cdots & \langle \mathbf_j, \mathbf_ \rangle \\ \mathbf_1 & \mathbf_2 & \cdots & \mathbf_j \end$

$\mathbf_j = \frac \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_ \rangle & \langle \mathbf_2, \mathbf_ \rangle & \cdots & \langle \mathbf_j, \mathbf_ \rangle \\ \mathbf_1 & \mathbf_2 & \cdots & \mathbf_j \end$

where ''D''₀=1 and, for ''j'' ≥ 1, ''D_j'' is the Gram determinant

$D_j = \begin \langle \mathbf_1, \mathbf_1 \rangle & \langle \mathbf_2, \mathbf_1 \rangle & \cdots & \langle \mathbf_j, \mathbf_1 \rangle \\ \langle \mathbf_1, \mathbf_2 \rangle & \langle \mathbf_2, \mathbf_2 \rangle & \cdots & \langle \mathbf_j, \mathbf_2 \rangle \\ \vdots & \vdots & \ddots & \vdots \\ \langle \mathbf_1, \mathbf_j \rangle & \langle \mathbf_2, \mathbf_j \rangle & \cdots & \langle \mathbf_j, \mathbf_j \rangle \end.$

Note that the expression for u_''k'' is a "formal" determinant, i.e. the matrix contains both scalars
and vectors; the meaning of this expression is defined to be the result of a cofactor expansion along the row of vectors.

The determinant formula for the Gram-Schmidt is computationally slower (exponentially slower) than the recursive algorithms described above; it is mainly of theoretical interest.

Expressed using geometric algebra

Expressed using notation used in geometric algebra, the unnormalized results of the Gram–Schmidt process can be expressed as
$\mathbf_k = \mathbf_k - \sum_^ (\mathbf_k \cdot \mathbf_j)\mathbf_j^\ ,$
which is equivalent to the expression using the $\operatorname$ operator defined above. The results can equivalently be expressed as
:$\mathbf_k = \mathbf_\wedge\mathbf_\wedge\cdot\cdot\cdot\wedge\mathbf_(\mathbf_\wedge\cdot\cdot\cdot\wedge\mathbf_)^,$
which is closely related to the expression using determinants above.

Alternatives

Other orthogonalization algorithms use Householder transformations or Givens rotations. The algorithms using Householder transformations are more stable than the stabilized Gram–Schmidt process. On the other hand, the Gram–Schmidt process produces the $j$th orthogonalized vector after the $j$th iteration, while orthogonalization using Householder reflections produces all the vectors only at the end. This makes only the Gram–Schmidt process applicable for iterative methods like the Arnoldi iteration.

Yet another alternative is motivated by the use of Cholesky decomposition for inverting the matrix of the normal equations in linear least squares. Let $V$ be a full column rank matrix, whose columns need to be orthogonalized. The matrix $V^* V$ is Hermitian and positive definite, so it can be written as $V^* V = L L^*,$ using the Cholesky decomposition. The lower triangular matrix $L$ with strictly positive diagonal entries is invertible. Then columns of the matrix $U = V\left(L^\right)^*$ are orthonormal and span the same subspace as the columns of the original matrix $V$. The explicit use of the product $V^* V$ makes the algorithm unstable, especially if the product's condition number is large. Nevertheless, this algorithm is used in practice and implemented in some software packages because of its high efficiency and simplicity.

In quantum mechanics there are several orthogonalization schemes with characteristics better suited for certain applications than original Gram–Schmidt. Nevertheless, it remains a popular and effective algorithm for even the largest electronic structure calculations.

References

Sources

* .
* .
* .
* .

External links

*

Harvey Mudd College Math Tutorial on the Gram-Schmidt algorithm


The entry "Gram-Schmidt orthogonalization" has some information and references on the origins of the method.
* Demos
Gram Schmidt process in plane
an
Gram Schmidt process in space




* Proof: ttp://planetmath.org/ProofOfGramSchmidtOrthogonalizationProcedure Raymond Puzio, Keenan Kidwell. "proof of Gram-Schmidt orthogonalization algorithm" (version 8). PlanetMath.org.

{{DEFAULTSORT:Gram-Schmidt Process
Linear algebra
Functional analysis
Articles with example MATLAB/Octave code