Extensive-form game on:
[Wikipedia]
[Google]
[Amazon]
In
Infinite Games (section 1.1), Yurii Khomskii (2010)"Infinite Chess, PBS Infinite Series"
PBS Infinite Series. Perfect information defined at 0:25, with academic sources and . A game over an expectminimax tree, like that of
 The game on the right has two players: 1 and 2. The numbers by every non-terminal node indicate to which player that decision node belongs. The numbers by every terminal node represent the payoffs to the players (e.g. 2,1 represents a payoff of 2 to player 1 and a payoff of 1 to player 2). The labels by every edge of the graph are the name of the action that edge represents.
The initial node belongs to player 1, indicating that player 1 moves first. Play according to the tree is as follows: player 1 chooses between ''U'' and ''D''; player 2 observes player 1's choice and then chooses between ''U' '' and ''D' ''. The payoffs are as specified in the tree. There are four outcomes represented by the four terminal nodes of the tree: (U,U'), (U,D'), (D,U') and (D,D'). The payoffs associated with each outcome respectively are as follows (0,0), (2,1), (1,2) and (3,1).
If player 1 plays ''D'', player 2 will play ''U' '' to maximise their payoff and so player 1 will only receive 1. However, if player 1 plays ''U'', player 2 maximises their payoff by playing ''D' '' and player 1 receives 2. Player 1 prefers 2 to 1 and so will play ''U'' and player 2 will play ''D' ''. This is the
The game on the right has two players: 1 and 2. The numbers by every non-terminal node indicate to which player that decision node belongs. The numbers by every terminal node represent the payoffs to the players (e.g. 2,1 represents a payoff of 2 to player 1 and a payoff of 1 to player 2). The labels by every edge of the graph are the name of the action that edge represents.
The initial node belongs to player 1, indicating that player 1 moves first. Play according to the tree is as follows: player 1 chooses between ''U'' and ''D''; player 2 observes player 1's choice and then chooses between ''U' '' and ''D' ''. The payoffs are as specified in the tree. There are four outcomes represented by the four terminal nodes of the tree: (U,U'), (U,D'), (D,U') and (D,D'). The payoffs associated with each outcome respectively are as follows (0,0), (2,1), (1,2) and (3,1).
If player 1 plays ''D'', player 2 will play ''U' '' to maximise their payoff and so player 1 will only receive 1. However, if player 1 plays ''U'', player 2 maximises their payoff by playing ''D' '' and player 1 receives 2. Player 1 prefers 2 to 1 and so will play ''U'' and player 2 will play ''D' ''. This is the
 If a game has an information set with more than one member that game is said to have
If a game has an information set with more than one member that game is said to have
 The game on the left is one of complete information (all the players and payoffs are known to everyone) but of imperfect information (the employer doesn't know what nature's move was.) The initial node is in the centre and it is not filled, so nature moves first. Nature selects with the same probability the type of player 1 (which in this game is tantamount to selecting the payoffs in the subgame played), either t1 or t2. Player 1 has distinct information sets for these; i.e. player 1 knows what type they are (this need not be the case). However, player 2 does not observe nature's choice. They do not know the type of player 1; however, in this game they do observe player 1's actions; i.e. there is perfect information. Indeed, it is now appropriate to alter the above definition of complete information: at every stage in the game, every player knows what has been played ''by the other players''. In the case of private information, every player knows what has been played by nature. Information sets are represented as before by broken lines.
In this game, if nature selects t1 as player 1's type, the game played will be like the very first game described, except that player 2 does not know it (and the very fact that this cuts through their information sets disqualify it from subgame status). There is one ''separating''
The game on the left is one of complete information (all the players and payoffs are known to everyone) but of imperfect information (the employer doesn't know what nature's move was.) The initial node is in the centre and it is not filled, so nature moves first. Nature selects with the same probability the type of player 1 (which in this game is tantamount to selecting the payoffs in the subgame played), either t1 or t2. Player 1 has distinct information sets for these; i.e. player 1 knows what type they are (this need not be the case). However, player 2 does not observe nature's choice. They do not know the type of player 1; however, in this game they do observe player 1's actions; i.e. there is perfect information. Indeed, it is now appropriate to alter the above definition of complete information: at every stage in the game, every player knows what has been played ''by the other players''. In the case of private information, every player knows what has been played by nature. Information sets are represented as before by broken lines.
In this game, if nature selects t1 as player 1's type, the game played will be like the very first game described, except that player 2 does not know it (and the very fact that this cuts through their information sets disqualify it from subgame status). There is one ''separating''
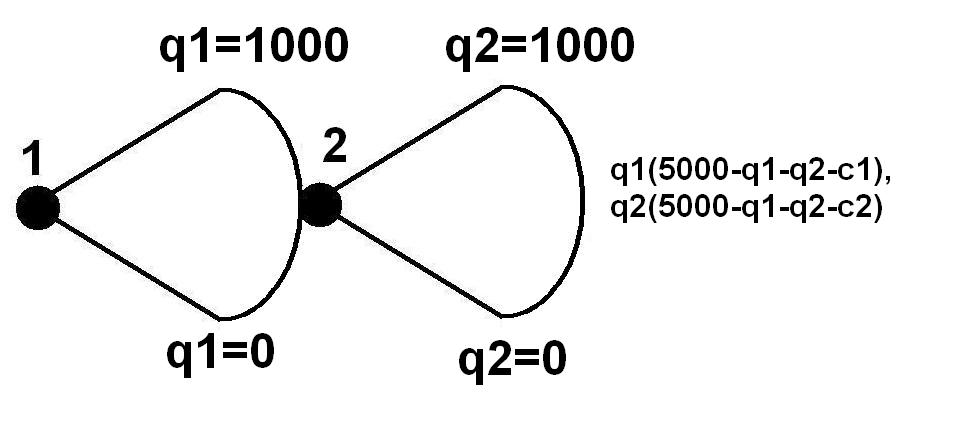 The tree on the left represents such a game, either with infinite action spaces (any
The tree on the left represents such a game, either with infinite action spaces (any
Free online
at many universities. * Luce R.D. and Raiffa H. (1957). Games and decisions: introduction and critical survey. (Ch3: Extensive and Normal Forms, pp39–55). Wiley New York. * Osborne MJ and Rubinstein A. 1994. A course in game theory (Ch6 Extensive game with perfect information, pp. 89–115). MIT press. * . A comprehensive reference from a computational perspective; see Chapter 5
Downloadable free online
game theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed ...
, an extensive-form game is a specification of a game
A game is a structured type of play usually undertaken for entertainment or fun, and sometimes used as an educational tool. Many games are also considered to be work (such as professional players of spectator sports or video games) or art ...
allowing for the explicit representation of a number of key aspects, like the sequencing of players' possible moves, their choices at every decision point, the (possibly imperfect
The imperfect ( abbreviated ) is a verb form that combines past tense (reference to a past time) and imperfective aspect (reference to a continuing or repeated event or state). It can have meanings similar to the English "was doing (something)" o ...
) information each player has about the other player's moves when they make a decision, and their payoffs for all possible game outcomes. Extensive-form games also allow for the representation of incomplete information
In economics and game theory, complete information is an economic situation or game in which knowledge about other market participants or players is available to all participants. The utility functions (including risk aversion), payoffs, strategies ...
in the form of chance events modeled as " moves by nature". Extensive-form representations differ from normal-form in that they provide a more complete description of the game in question, whereas normal-form simply boils down the game into a payoff matrix.
Finite extensive-form games
Some authors, particularly in introductory textbooks, initially define the extensive-form game as being just agame tree
In the context of combinatorial game theory, a game tree is a graph representing all possible game states within a sequential game that has perfect information. Such games include chess, checkers, Go, and tic-tac-toe.
A game tree can be us ...
with payoffs (no imperfect or incomplete information), and add the other elements in subsequent chapters as refinements. Whereas the rest of this article follows this gentle approach with motivating examples, we present upfront the finite extensive-form games as (ultimately) constructed here. This general definition was introduced by Harold W. Kuhn in 1953, who extended an earlier definition of von Neumann from 1928. Following the presentation from , an ''n''-player extensive-form game thus consists of the following:
* A finite set of ''n'' (rational) players
* A rooted tree
In graph theory, a tree is an undirected graph in which any two vertices are connected by path, or equivalently a connected acyclic undirected graph. A forest is an undirected graph in which any two vertices are connected by path, or equi ...
, called the ''game tree''
* Each terminal (leaf) node of the game tree has an ''n''-tuple of ''payoffs'', meaning there is one payoff for each player at the end of every possible play
* A partition of the non-terminal nodes of the game tree in ''n''+1 subsets, one for each (rational) player, and with a special subset for a fictitious player called Chance (or Nature). Each player's subset of nodes is referred to as the "nodes of the player". (A game of complete information thus has an empty set of Chance nodes.)
* Each node of the Chance player has a probability distribution
In probability theory and statistics, a probability distribution is a Function (mathematics), function that gives the probabilities of occurrence of possible events for an Experiment (probability theory), experiment. It is a mathematical descri ...
over its outgoing edges.
* Each set of nodes of a rational player is further partitioned in information sets, which make certain choices indistinguishable for the player when making a move, in the sense that:
** there is a one-to-one correspondence between outgoing edges of any two nodes of the same information set—thus the set of all outgoing edges of an information set is partitioned in equivalence class
In mathematics, when the elements of some set S have a notion of equivalence (formalized as an equivalence relation), then one may naturally split the set S into equivalence classes. These equivalence classes are constructed so that elements ...
es, each class representing a possible choice for a player's move at some point—, and
** every (directed) path in the tree from the root to a terminal node can cross each information set at most once
* the complete description of the game specified by the above parameters is common knowledge
Common knowledge is knowledge that is publicly known by everyone or nearly everyone, usually with reference to the community in which the knowledge is referenced. Common knowledge can be about a broad range of subjects, such as science, litera ...
among the players
A play is thus a path through the tree from the root to a terminal node. At any given non-terminal node belonging to Chance, an outgoing branch is chosen according to the probability distribution. At any rational player's node, the player must choose one of the equivalence classes for the edges, which determines precisely one outgoing edge except (in general) the player doesn't know which one is being followed. (An outside observer knowing every other player's choices up to that point, and the realization of Nature's moves, can determine the edge precisely.) A pure strategy
In game theory, a move, action, or play is any one of the options which a player can choose in a setting where the optimal outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the actio ...
for a player thus consists of a selection
Selection may refer to:
Science
* Selection (biology), also called natural selection, selection in evolution
** Sex selection, in genetics
** Mate selection, in mating
** Sexual selection in humans, in human sexuality
** Human mating strat ...
—choosing precisely one class of outgoing edges for every information set (of his). In a game of perfect information, the information sets are singletons. It's less evident how payoffs should be interpreted in games with Chance nodes. It is assumed that each player has a von Neumann–Morgenstern utility function
The expected utility hypothesis is a foundational assumption in mathematical economics concerning decision making under uncertainty. It postulates that rational agents maximize utility, meaning the subjective desirability of their actions. Rational ...
defined for every game outcome; this assumption entails that every rational player will evaluate an a priori
('from the earlier') and ('from the later') are Latin phrases used in philosophy to distinguish types of knowledge, Justification (epistemology), justification, or argument by their reliance on experience. knowledge is independent from any ...
random outcome by its expected utility.
The above presentation, while precisely defining the mathematical structure over which the game is played, elides however the more technical discussion of formalizing statements about how the game is played like "a player cannot distinguish between nodes in the same information set when making a decision". These can be made precise using epistemic modal logic
Epistemic modal logic is a subfield of modal logic that is concerned with reasoning about knowledge. While epistemology has a long philosophical tradition dating back to Ancient Greece, epistemic logic is a much more recent development with appl ...
; see for details.
A perfect information
Perfect information is a concept in game theory and economics that describes a situation where all players in a game or all participants in a market have knowledge of all relevant information in the system. This is different than complete informat ...
two-player game over a game tree
In the context of combinatorial game theory, a game tree is a graph representing all possible game states within a sequential game that has perfect information. Such games include chess, checkers, Go, and tic-tac-toe.
A game tree can be us ...
(as defined in combinatorial game theory
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Research in this field has primarily focused on two-player games in which a ''position'' ev ...
and artificial intelligence
Artificial intelligence (AI) is the capability of computer, computational systems to perform tasks typically associated with human intelligence, such as learning, reasoning, problem-solving, perception, and decision-making. It is a field of re ...
) can be represented as an extensive form game with outcomes (i.e. win, lose, or draw
Draw, drawing, draws, or drawn most commonly refer to:
* Draw (terrain), a terrain feature formed by two parallel ridges or spurs with low ground in between them
* Draw (tie), in a competition, where competitors achieve equal outcomes
* Draw ...
). Examples of such games include tic-tac-toe
Tic-tac-toe (American English), noughts and crosses (English in the Commonwealth of Nations, Commonwealth English), or Xs and Os (Canadian English, Canadian or Hiberno-English, Irish English) is a paper-and-pencil game for two players who ta ...
, chess
Chess is a board game for two players. It is an abstract strategy game that involves Perfect information, no hidden information and no elements of game of chance, chance. It is played on a square chessboard, board consisting of 64 squares arran ...
, and infinite chess
Infinite chess is any variation of the game of chess played on an unbounded chessboard. Versions of infinite chess have been introduced independently by multiple players, chess theorists, and mathematicians, both as a playable game and as a mod ...
.https://www.math.uni-hamburg/Infinite Games, Yurii Khomskii (2010)Infinite Games (section 1.1), Yurii Khomskii (2010)"Infinite Chess, PBS Infinite Series"
PBS Infinite Series. Perfect information defined at 0:25, with academic sources and . A game over an expectminimax tree, like that of
backgammon
Backgammon is a two-player board game played with counters and dice on tables boards. It is the most widespread Western member of the large family of tables games, whose ancestors date back at least 1,600 years. The earliest record of backgammo ...
, has no imperfect information (all information sets are singletons) but has moves of chance. For example, poker
Poker is a family of Card game#Comparing games, comparing card games in which Card player, players betting (poker), wager over which poker hand, hand is best according to that specific game's rules. It is played worldwide, with varying rules i ...
has both moves of chance (the cards being dealt) and imperfect information (the cards secretly held by other players).
Perfect and complete information
A complete extensive-form representation specifies: # the players of a game # for every player every opportunity they have to move # what each player can do at each of their moves # what each player knows for every move # the payoffs received by every player for every possible combination of movessubgame perfect equilibrium
In game theory, a subgame perfect equilibrium (SPE), or subgame perfect Nash equilibrium (SPNE), is a refinement of the Nash equilibrium concept, specifically designed for dynamic games where players make sequential decisions. A strategy profil ...
.
Imperfect information
An advantage of representing the game in this way is that it is clear what the order of play is. The tree shows clearly that player 1 moves first and player 2 observes this move. However, in some games play does not occur like this. One player does not always observe the choice of another (for example, moves may be simultaneous or a move may be hidden). An information set is a set of decision nodes such that: # Every node in the set belongs to one player. # When the game reaches the information set, the player who is about to move cannot differentiate between nodes within the information set; i.e. if the information set contains more than one node, the player to whom that set belongs does not know which node in the set has been reached. In extensive form, an information set is indicated by a dotted line connecting all nodes in that set or sometimes by a loop drawn around all the nodes in that set.imperfect information
The imperfect ( abbreviated ) is a verb form that combines past tense (reference to a past time) and imperfective aspect (reference to a continuing or repeated event or state). It can have meanings similar to the English "was doing (something)" o ...
. A game with perfect information is such that at any stage of the game, every player knows exactly what has taken place earlier in the game; i.e. every information set is a singleton set. Any game without perfect information has imperfect information.
The game on the right is the same as the above game except that player 2 does not know what player 1 does when they come to play. The first game described has perfect information; the game on the right does not. If both players are rational and both know that both players are rational and everything that is known by any player is known to be known by every player (i.e. player 1 knows player 2 knows that player 1 is rational and player 2 knows this, etc. ''ad infinitum''), play in the first game will be as follows: player 1 knows that if they play ''U'', player 2 will play ''D' '' (because for player 2 a payoff of 1 is preferable to a payoff of 0) and so player 1 will receive 2. However, if player 1 plays ''D'', player 2 will play ''U' '' (because to player 2 a payoff of 2 is better than a payoff of 1) and player 1 will receive 1. Hence, in the first game, the equilibrium will be (''U'', ''D' '') because player 1 prefers to receive 2 to 1 and so will play ''U'' and so player 2 will play ''D' ''.
In the second game it is less clear: player 2 cannot observe player 1's move. Player 1 would like to fool player 2 into thinking they have played ''U'' when they have actually played ''D'' so that player 2 will play ''D' '' and player 1 will receive 3. In fact in the second game there is a perfect Bayesian equilibrium
In game theory, a Bayesian game is a strategic decision-making model which assumes players have incomplete information. Players may hold private information relevant to the game, meaning that the payoffs are not common knowledge. Bayesian games mo ...
where player 1 plays ''D'' and player 2 plays ''U' '' and player 2 holds the belief that player 1 will definitely play ''D''. In this equilibrium, every strategy is rational given the beliefs held and every belief is consistent with the strategies played. Notice how the imperfection of information changes the outcome of the game.
To more easily solve this game for the Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player could gain by changing their own strategy (holding all other players' strategies fixed) ...
, it can be converted to the normal form. Given this is a simultaneous
Simultaneity may refer to:
* Relativity of simultaneity, a concept in special relativity.
* Simultaneity (music), more than one complete musical texture occurring at the same time, rather than in succession
* Simultaneity, a concept in Endogenei ...
/sequential
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is call ...
game, player one and player two each have two strategies
Strategy (from Greek στρατηγία ''stratēgia'', "troop leadership; office of general, command, generalship") is a general plan to achieve one or more long-term or overall goals under conditions of uncertainty. In the sense of the "art o ...
.
* Player 1's Strategies:
* Player 2's Strategies:
We will have a two by two matrix with a unique payoff for each combination of moves. Using the normal form game, it is now possible to solve the game and identify dominant strategies for both players.
* If player 1 plays Up (U), player 2 prefers to play Down (D’) (Payoff 1>0)
* If player 1 plays Down (D), player 2 prefers to play Up (U’) (Payoff 2>1)
* If player 2 plays Up (U’), player 1 prefers to play Down (D) (Payoff 1>0)
* If player 2 plays Down (D’), player 1 prefers to play Down (D) (3>2)
These preferences can be marked within the matrix, and any box where both players have a preference provides a nash equilibrium. This particular game has a single solution of (D,U’) with a payoff of (1,2).
In games with infinite action spaces and imperfect information, non-singleton information sets are represented, if necessary, by inserting a dotted line connecting the (non-nodal) endpoints behind the arc described above or by dashing the arc itself. In the Stackelberg competition described above, if the second player had not observed the first player's move the game would no longer fit the Stackelberg model; it would be Cournot competition
Cournot competition is an economic model used to describe an industry structure in which companies compete on the amount of output they will produce, which they decide on independently of each other and at the same time. It is named after Antoine ...
.
Incomplete information
It may be the case that a player does not know exactly what the payoffs of the game are or of what type their opponents are. This sort of game hasincomplete information
In economics and game theory, complete information is an economic situation or game in which knowledge about other market participants or players is available to all participants. The utility functions (including risk aversion), payoffs, strategies ...
. In extensive form it is represented as a game with complete but imperfect information using the so-called Harsanyi transformation. This transformation introduces to the game the notion of '' nature's choice'' or ''God's choice''. Consider a game consisting of an employer considering whether to hire a job applicant. The job applicant's ability might be one of two things: high or low. Their ability level is random; they either have low ability with probability 1/3 or high ability with probability 2/3. In this case, it is convenient to model nature as another player of sorts who chooses the applicant's ability according to those probabilities. Nature however does not have any payoffs. Nature's choice is represented in the game tree by a non-filled node. Edges coming from a nature's choice node are labelled with the probability of the event it represents occurring.
perfect Bayesian equilibrium
In game theory, a Bayesian game is a strategic decision-making model which assumes players have incomplete information. Players may hold private information relevant to the game, meaning that the payoffs are not common knowledge. Bayesian games mo ...
; i.e. an equilibrium in which different types do different things.
If both types play the same action (pooling), an equilibrium cannot be sustained. If both play ''D'', player 2 can only form the belief that they are on either node in the information set with probability 1/2 (because this is the chance of seeing either type). Player 2 maximises their payoff by playing ''D' ''. However, if they play ''D' '', type 2 would prefer to play ''U''. This cannot be an equilibrium. If both types play ''U'', player 2 again forms the belief that they are at either node with probability 1/2. In this case player 2 plays ''D' '', but then type 1 prefers to play ''D''.
If type 1 plays ''U'' and type 2 plays ''D'', player 2 will play ''D' '' whatever action they observe, but then type 1 prefers ''D''. The only equilibrium hence is with type 1 playing ''D'', type 2 playing ''U'' and player 2 playing ''U' '' if they observe ''D'' and randomising if they observe ''U''. Through their actions, player 1 has signalled their type to player 2.
Formal definition
Formally, a finite game in extensive form is a structure where: * is a finite tree with a set of nodes , a unique initial node , a set of terminal nodes (let be a set of decision nodes) and an immediate predecessor function on which the rules of the game are represented, * is a partition of called an information partition, * is a set of actions available for each information set which forms a partition on the set of all actions . * is an action partition associating each node to a single action , fulfilling: , the restriction of on is a bijection, with the set of successor nodes of . * is a finite set of players, is (a special player called) nature, and is a player partition of information set . Let be a single player that makes a move at node . * is a family of probabilities of the actions of nature, and * is a payoff profile function.Infinite action space
It may be that a player has an infinite number of possible actions to choose from at a particular decision node. The device used to represent this is an arc joining two edges protruding from the decision node in question. If the action space is a continuum between two numbers, the lower and upper delimiting numbers are placed at the bottom and top of the arc respectively, usually with a variable that is used to express the payoffs. The infinite number of decision nodes that could result are represented by a single node placed in the centre of the arc. A similar device is used to represent action spaces that, whilst not infinite, are large enough to prove impractical to represent with an edge for each action.real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
between 0 and 5000) or with very large action spaces (perhaps any integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
between 0 and 5000). This would be specified elsewhere. Here, it will be supposed that it is the former and, for concreteness, it will be supposed it represents two firms engaged in Stackelberg competition. The payoffs to the firms are represented on the left, with and as the strategy they adopt and and as some constants (here marginal costs to each firm). The subgame perfect Nash equilibria of this game can be found by taking the first partial derivative of each payoff function with respect to the follower's (firm 2) strategy variable () and finding its best response
In game theory, the best response is the strategy (or strategies) which produces the most favorable outcome for a player, taking other players' strategies as given. The concept of a best response is central to John Nash's best-known contribution ...
function, . The same process can be done for the leader except that in calculating its profit, it knows that firm 2 will play the above response and so this can be substituted into its maximisation problem. It can then solve for by taking the first derivative, yielding . Feeding this into firm 2's best response function, and is the subgame perfect Nash equilibrium.
See also
*Axiom of determinacy
In mathematics, the axiom of determinacy (abbreviated as AD) is a possible axiom for set theory introduced by Jan Mycielski and Hugo Steinhaus in 1962. It refers to certain two-person topological games of length ω. AD states that every game o ...
* Perfect information
Perfect information is a concept in game theory and economics that describes a situation where all players in a game or all participants in a market have knowledge of all relevant information in the system. This is different than complete informat ...
* Combinatorial game theory
Combinatorial game theory is a branch of mathematics and theoretical computer science that typically studies sequential games with perfect information. Research in this field has primarily focused on two-player games in which a ''position'' ev ...
* Self-confirming equilibrium
In game theory, self-confirming equilibrium is a generalization of Nash equilibrium
In game theory, the Nash equilibrium is the most commonly used solution concept for non-cooperative games. A Nash equilibrium is a situation where no player c ...
* Sequential game
In game theory, a sequential game is defined as a game where one player selects their action before others, and subsequent players are informed of that choice before making their own decisions. This turn-based structure, governed by a time axis, d ...
* Signalling
A signal is both the process and the result of transmission of data over some media accomplished by embedding some variation. Signals are important in multiple subject fields including signal processing, information theory and biology.
In ...
* Solution concept
In game theory, a solution concept is a formal rule for predicting how a game will be played. These predictions are called "solutions", and describe which strategies will be adopted by players and, therefore, the result of the game. The most comm ...
References
* * * Dresher M. (1961). The mathematics of games of strategy: theory and applications (Ch4: Games in extensive form, pp74–78). Rand Corp. * Fudenberg D and Tirole J. (1991) Game theory (Ch3 Extensive form games, pp67–106). MIT press. * . An 88-page mathematical introduction; see Chapters 4 and 5Free online
at many universities. * Luce R.D. and Raiffa H. (1957). Games and decisions: introduction and critical survey. (Ch3: Extensive and Normal Forms, pp39–55). Wiley New York. * Osborne MJ and Rubinstein A. 1994. A course in game theory (Ch6 Extensive game with perfect information, pp. 89–115). MIT press. * . A comprehensive reference from a computational perspective; see Chapter 5
Downloadable free online
Further reading
* , 6.1, "Disasters in Game Theory" and 7.2 "Measurability (The Axiom of Determinateness)", discusses problems in extending the finite-case definition to infinite number of options (or moves) Historical papers * * contains Kuhn's lectures at Princeton from 1952 (officially unpublished previously, but in circulation as photocopies) {{DEFAULTSORT:Extensive-Form Game Game theory game classes