Benoit Mandelbrot on:
[Wikipedia]
[Google]
[Amazon]
Benoit B. Mandelbrot (20 November 1924 – 14 October 2010) was a Polish-born French-American
 In 1975, Mandelbrot coined the term ''
In 1975, Mandelbrot coined the term '' Mandelbrot, however, never felt he was inventing a new idea. He described his feelings in a documentary with science writer Arthur C. Clarke:
According to Clarke, "the
Mandelbrot, however, never felt he was inventing a new idea. He described his feelings in a documentary with science writer Arthur C. Clarke:
According to Clarke, "the
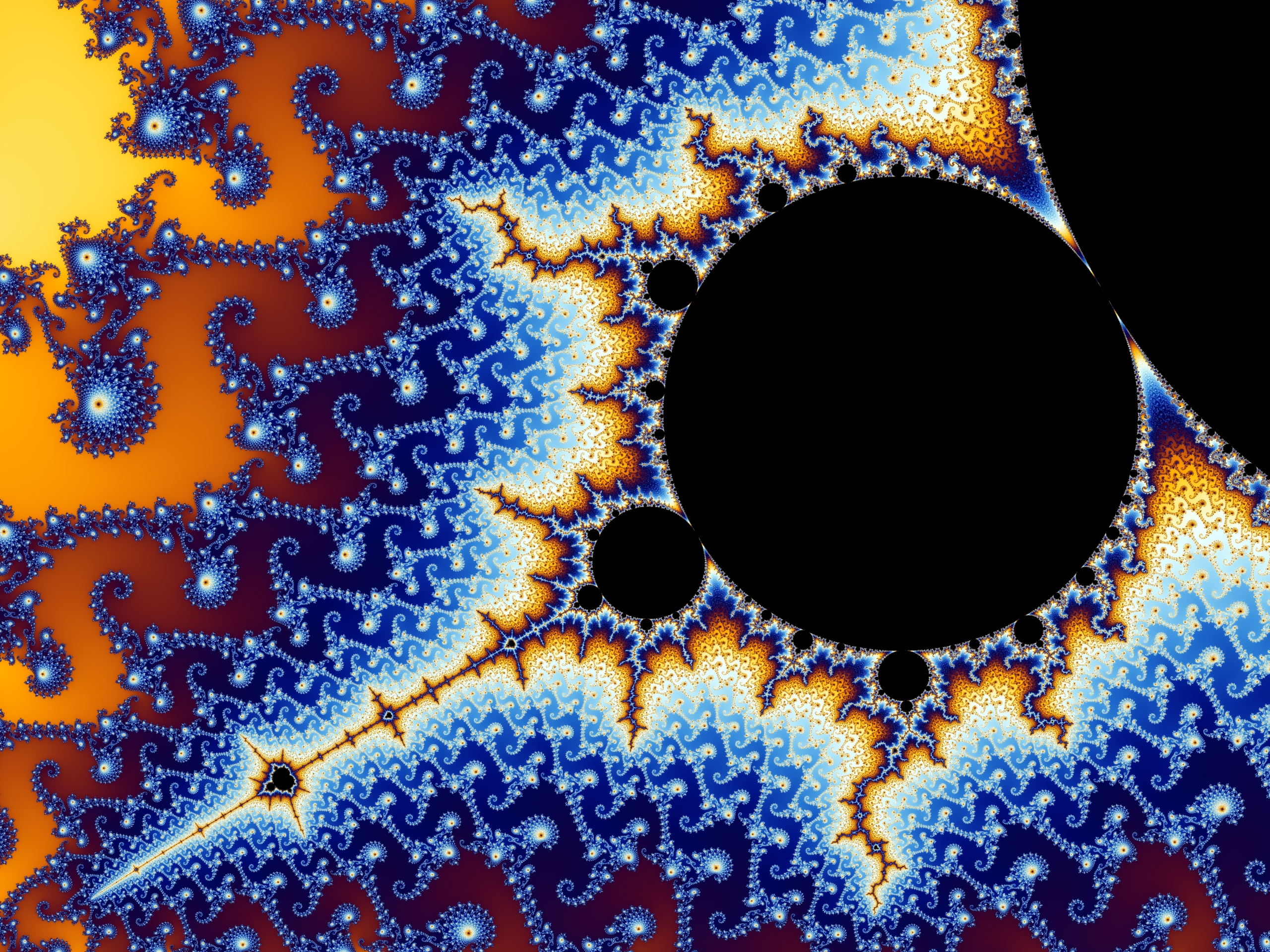 Mandelbrot has been called an artist, and a visionary and a maverick. His informal and passionate style of writing and his emphasis on visual and geometric intuition (supported by the inclusion of numerous illustrations) made ''The Fractal Geometry of Nature'' accessible to non-specialists. The book sparked widespread popular interest in fractals and contributed to chaos theory and other fields of science and mathematics.
Mandelbrot also put his ideas to work in cosmology. He offered in 1974 a new explanation of
Mandelbrot has been called an artist, and a visionary and a maverick. His informal and passionate style of writing and his emphasis on visual and geometric intuition (supported by the inclusion of numerous illustrations) made ''The Fractal Geometry of Nature'' accessible to non-specialists. The book sparked widespread popular interest in fractals and contributed to chaos theory and other fields of science and mathematics.
Mandelbrot also put his ideas to work in cosmology. He offered in 1974 a new explanation of
. japanprize.jp and the Einstein Lectureship of the
Benoît Mandelbrot's obituary
. ''The Economist'' (21 October 2010) Best-selling essayist-author
''The Fractalist, Memoir of a Scientific Maverick.''
New York
Vintage Books
Division of Random House. * ''The Fractalist: Memoir of a Scientific Maverick'', 2014 * *
"Hunting the Hidden Dimension: mysteriously beautiful fractals are shaking up the world of mathematics and deepening our understanding of nature"
''
Mandelbrot's page at Yale
(TED address).
Fractals in Science, Engineering and Finance
(lecture).
FT.com interview
on the subject of the financial markets which includes his critique of the "efficient market" hypothesis. *
Mandelbrot relates his life story
(
Interview (1 January 1981, Ithaca, NY)
held by the
Video animation of Mandelbrot set
zoom factor 10342. * , a three-dimensional Mandelbrot-set projection. * * *
Michael Frame, "Benoit B. Mandelbrot", Biographical Memoirs of the National Academy of Sciences (2014)
{{DEFAULTSORT:Mandelbrot, Benoit 1924 births 2010 deaths 20th-century American economists 20th-century American mathematicians 20th-century French mathematicians 21st-century American economists 21st-century American mathematicians 21st-century French mathematicians California Institute of Technology alumni Chaos theorists Deaths from cancer in Massachusetts Deaths from pancreatic cancer École Polytechnique alumni Fellows of the American Geophysical Union Fellows of the American Physical Society Fellows of the American Statistical Association Fellows of the Econometric Society French emigrants to the United States Harvard University people IBM Fellows IBM Research computer scientists IBM employees Institute for Advanced Study visiting scholars Jewish French scientists Members of the Norwegian Academy of Science and Letters Members of the United States National Academy of Sciences Officiers of the Légion d'honneur 20th-century Polish Jews Polish emigrants to France Polish people of Lithuanian descent University of Paris alumni Wolf Prize in Physics laureates Yale Sterling Professors Yale University faculty Members of the American Philosophical Society
mathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
and polymath
A polymath ( el, πολυμαθής, , "having learned much"; la, homo universalis, "universal human") is an individual whose knowledge spans a substantial number of subjects, known to draw on complex bodies of knowledge to solve specific pro ...
with broad interests in the practical sciences, especially regarding what he labeled as "the art of roughness" of physical phenomena and "the uncontrolled element in life". He referred to himself as a "fractalist" and is recognized for his contribution to the field of fractal geometry
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
, which included coining the word "fractal", as well as developing a theory of "roughness and self-similarity
__NOTOC__
In mathematics, a self-similar object is exactly or approximately similar to a part of itself (i.e., the whole has the same shape as one or more of the parts). Many objects in the real world, such as coastlines, are statistically se ...
" in nature.
In 1936, at the age of 11, Mandelbrot and his family emigrated from Warsaw
Warsaw ( pl, Warszawa, ), officially the Capital City of Warsaw,, abbreviation: ''m.st. Warszawa'' is the capital and largest city of Poland. The metropolis stands on the River Vistula in east-central Poland, and its population is officia ...
, Poland, to France. After World War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposin ...
ended, Mandelbrot studied mathematics, graduating from universities in Paris and in the United States and receiving a master's degree in aeronautics
Aeronautics is the science or art involved with the study, design, and manufacturing of air flight–capable machines, and the techniques of operating aircraft and rockets within the atmosphere. The British Royal Aeronautical Society identifies ...
from the California Institute of Technology
The California Institute of Technology (branded as Caltech or CIT)The university itself only spells its short form as "Caltech"; the institution considers other spellings such a"Cal Tech" and "CalTech" incorrect. The institute is also occasional ...
. He spent most of his career in both the United States and France, having dual French and American
American(s) may refer to:
* American, something of, from, or related to the United States of America, commonly known as the "United States" or "America"
** Americans, citizens and nationals of the United States of America
** American ancestry, pe ...
citizenship. In 1958, he began a 35-year career at IBM, where he became an IBM Fellow
An IBM Fellow is an appointed position at IBM made by IBM's CEO. Typically only four to nine (eleven in 2014) IBM Fellows are appointed each year, in May or June. Fellow is the highest honor a scientist, engineer, or programmer at IBM can achie ...
, and periodically took leaves of absence to teach at Harvard University
Harvard University is a private Ivy League research university in Cambridge, Massachusetts. Founded in 1636 as Harvard College and named for its first benefactor, the Puritan clergyman John Harvard, it is the oldest institution of higher le ...
. At Harvard, following the publication of his study of U.S. commodity markets in relation to cotton futures, he taught economics and applied sciences.
Because of his access to IBM's computers, Mandelbrot was one of the first to use computer graphics to create and display fractal geometric images, leading to his discovery of the Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
in 1980. He showed how visual complexity can be created from simple rules. He said that things typically considered to be "rough", a "mess", or "chaotic", such as clouds or shorelines, actually had a "degree of order". His math and geometry-centered research included contributions to such fields as statistical physics
Statistical physics is a branch of physics that evolved from a foundation of statistical mechanics, which uses methods of probability theory and statistics, and particularly the Mathematics, mathematical tools for dealing with large populations ...
, meteorology
Meteorology is a branch of the atmospheric sciences (which include atmospheric chemistry and physics) with a major focus on weather forecasting. The study of meteorology dates back millennia, though significant progress in meteorology did not ...
, hydrology
Hydrology () is the scientific study of the movement, distribution, and management of water on Earth and other planets, including the water cycle, water resources, and environmental watershed sustainability. A practitioner of hydrology is calle ...
, geomorphology
Geomorphology (from Ancient Greek: , ', "earth"; , ', "form"; and , ', "study") is the scientific study of the origin and evolution of topographic and bathymetric features created by physical, chemical or biological processes operating at or n ...
, anatomy
Anatomy () is the branch of biology concerned with the study of the structure of organisms and their parts. Anatomy is a branch of natural science that deals with the structural organization of living things. It is an old science, having its ...
, taxonomy
Taxonomy is the practice and science of categorization or classification.
A taxonomy (or taxonomical classification) is a scheme of classification, especially a hierarchical classification, in which things are organized into groups or types. ...
, neurology
Neurology (from el, wikt:νεῦρον, νεῦρον (neûron), "string, nerve" and the suffix wikt:-logia, -logia, "study of") is the branch of specialty (medicine), medicine dealing with the diagnosis and treatment of all categories of co ...
, linguistics
Linguistics is the scientific study of human language. It is called a scientific study because it entails a comprehensive, systematic, objective, and precise analysis of all aspects of language, particularly its nature and structure. Linguis ...
, information technology
Information technology (IT) is the use of computers to create, process, store, retrieve, and exchange all kinds of data . and information. IT forms part of information and communications technology (ICT). An information technology system (I ...
, computer graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great de ...
, economics
Economics () is the social science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services.
Economics focuses on the behaviour and intera ...
, geology
Geology () is a branch of natural science concerned with Earth and other astronomical objects, the features or rocks of which it is composed, and the processes by which they change over time. Modern geology significantly overlaps all other Ear ...
, medicine
Medicine is the science and practice of caring for a patient, managing the diagnosis, prognosis, prevention, treatment, palliation of their injury or disease, and promoting their health. Medicine encompasses a variety of health care pract ...
, physical cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of f ...
, engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, chaos theory
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have co ...
, econophysics
Econophysics is a Heterodox economics, heterodox interdisciplinary research field, applying theories and methods originally developed by physicists in order to solve problems in economics, usually those including uncertainty or stochastic processes ...
, metallurgy
Metallurgy is a domain of materials science and engineering that studies the physical and chemical behavior of metallic elements, their inter-metallic compounds, and their mixtures, which are known as alloys.
Metallurgy encompasses both the sc ...
, and the social science
Social science is one of the branches of science, devoted to the study of societies and the relationships among individuals within those societies. The term was formerly used to refer to the field of sociology, the original "science of soc ...
s.
Toward the end of his career, he was Sterling Professor of Mathematical Sciences at Yale University
Yale University is a private research university in New Haven, Connecticut. Established in 1701 as the Collegiate School, it is the third-oldest institution of higher education in the United States and among the most prestigious in the wo ...
, where he was the oldest professor in Yale's history to receive tenure.
Mandelbrot also held positions at the Pacific Northwest National Laboratory
Pacific Northwest National Laboratory (PNNL) is one of the United States Department of Energy national laboratories, managed by the Department of Energy's (DOE) Office of Science. The main campus of the laboratory is in Richland, Washington.
O ...
, Université Lille Nord de France
The Community of Universities and Institutions (COMUE) Lille Nord de France (formerly Université Lille Nord de France) was a French Groups of Universities and Institutions ( COMUE) spread over multiple campuses and centered in Lille (North - Hauts ...
, Institute for Advanced Study
The Institute for Advanced Study (IAS), located in Princeton, New Jersey, in the United States, is an independent center for theoretical research and intellectual inquiry. It has served as the academic home of internationally preeminent scholar ...
and Centre National de la Recherche Scientifique
The French National Centre for Scientific Research (french: link=no, Centre national de la recherche scientifique, CNRS) is the French state research organisation and is the largest fundamental science
Basic research, also called pure research o ...
. During his career, he received over 15 honorary doctorates and served on many science journals, along with winning numerous awards. His autobiography, ''The Fractalist: Memoir of a Scientific Maverick'', was published posthumously in 2012.
Early years
Benedykt Mandelbrot was born in aLithuanian Jewish
Lithuanian Jews or Litvaks () are Jews with roots in the territory of the former Grand Duchy of Lithuania (covering present-day Lithuania, Belarus, Latvia, the northeastern Suwałki and Białystok regions of Poland, as well as adjacent area ...
family, in Warsaw
Warsaw ( pl, Warszawa, ), officially the Capital City of Warsaw,, abbreviation: ''m.st. Warszawa'' is the capital and largest city of Poland. The metropolis stands on the River Vistula in east-central Poland, and its population is officia ...
during the Second Polish Republic
The Second Polish Republic, at the time officially known as the Republic of Poland, was a country in Central Europe, Central and Eastern Europe that existed between 1918 and 1939. The state was established on 6 November 1918, before the end of ...
. His father made his living trading clothing; his mother was a dental surgeon. During his first two school years, he was tutored privately by an uncle who despised rote learning
Rote learning is a memorization technique based on repetition. The method rests on the premise that the recall of repeated material becomes faster the more one repeats it. Some of the alternatives to rote learning include meaningful learning, ...
: "Most of my time was spent playing chess, reading maps and learning how to open my eyes to everything around me." In 1936, when he was 11, the family emigrated from Poland to France. The move, World War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposin ...
, and the influence of his father's brother, the mathematician Szolem Mandelbrojt (who had moved to Paris around 1920), further prevented a standard education. "The fact that my parents, as economic and political refugees, joined Szolem in France saved our lives," he writes.
Mandelbrot attended the Lycée Rollin (now the Collège-lycée Jacques-Decour
The Collège-lycée Jacques-Decour is a school in Paris, France, on avenue Trudaine.
History
The school was founded as the private Collège Sainte-Barbe in 1821 and renamed Collège Rollin in 1830. It was transplanted in 1876 from the Quartier ...
) in Paris until the start of World War II
World War II or the Second World War, often abbreviated as WWII or WW2, was a world war that lasted from 1939 to 1945. It involved the vast majority of the world's countries—including all of the great powers—forming two opposin ...
, when his family moved to Tulle
Tulle (; ) is a commune in central France. It is the third-largest town in the former region of Limousin and is the capital of the department of Corrèze, in the region of Nouvelle-Aquitaine. Tulle is also the episcopal see of the Roman Cat ...
, France. He was helped by Rabbi
A rabbi () is a spiritual leader or religious teacher in Judaism. One becomes a rabbi by being ordained by another rabbi – known as ''semikha'' – following a course of study of Jewish history and texts such as the Talmud. The basic form of ...
David Feuerwerker, the Rabbi of Brive-la-Gaillarde
Brive-la-Gaillarde (; Limousin dialect of oc, Briva la Galharda) is a commune of France. It is a sub-prefecture and the largest city of the Corrèze department. It has around 46,000 inhabitants, while the population of the agglomeration was 7 ...
, to continue his studies. Much of France was occupied by the Nazis at the time, and Mandelbrot recalls this period:
In 1944, Mandelbrot returned to Paris, studied at the Lycée du Parc
The Lycée du Parc is a public secondary school located in the sixth ''arrondissement'' of Lyon, France. Its name comes from the Parc de la Tête d'Or, one of Europe's largest urban parks, which is situated nearby.
It provides a ''lycée''-level ...
in Lyon
Lyon,, ; Occitan: ''Lion'', hist. ''Lionés'' also spelled in English as Lyons, is the third-largest city and second-largest metropolitan area of France. It is located at the confluence of the rivers Rhône and Saône, to the northwest of t ...
, and in 1945 to 1947 attended the École Polytechnique
École may refer to:
* an elementary school in the French educational stages normally followed by secondary education establishments (collège and lycée)
* École (river), a tributary of the Seine flowing in région Île-de-France
* École, Savoi ...
, where he studied under Gaston Julia
Gaston Maurice Julia (3 February 1893 – 19 March 1978) was a French Algerian mathematician who devised the formula for the Julia set. His works were popularized by French mathematician Benoit Mandelbrot; the Julia and Mandelbrot fractals are ...
and Paul Lévy. From 1947 to 1949 he studied at California Institute of Technology, where he earned a master's degree in aeronautics. Returning to France, he obtained his PhD degree
A Doctor of Philosophy (PhD, Ph.D., or DPhil; Latin: or ') is the most common degree at the highest academic level awarded following a course of study. PhDs are awarded for programs across the whole breadth of academic fields. Because it is ...
in Mathematical Sciences at the University of Paris
, image_name = Coat of arms of the University of Paris.svg
, image_size = 150px
, caption = Coat of Arms
, latin_name = Universitas magistrorum et scholarium Parisiensis
, motto = ''Hic et ubique terrarum'' (Latin)
, mottoeng = Here and a ...
in 1952.
Research career
From 1949 to 1958, Mandelbrot was a staff member at theCentre National de la Recherche Scientifique
The French National Centre for Scientific Research (french: link=no, Centre national de la recherche scientifique, CNRS) is the French state research organisation and is the largest fundamental science
Basic research, also called pure research o ...
. During this time he spent a year at the Institute for Advanced Study
The Institute for Advanced Study (IAS), located in Princeton, New Jersey, in the United States, is an independent center for theoretical research and intellectual inquiry. It has served as the academic home of internationally preeminent scholar ...
in Princeton, New Jersey
Princeton is a municipality with a borough form of government in Mercer County, in the U.S. state of New Jersey. It was established on January 1, 2013, through the consolidation of the Borough of Princeton and Princeton Township, both of whi ...
, where he was sponsored by John von Neumann
John von Neumann (; hu, Neumann János Lajos, ; December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. He was regarded as having perhaps the widest cove ...
. In 1955 he married Aliette Kagan and moved to Geneva, Switzerland
Geneva ( ; french: Genève ) frp, Genèva ; german: link=no, Genf ; it, Ginevra ; rm, Genevra is the List of cities in Switzerland, second-most populous city in Switzerland (after Zürich) and the most populous city of Romandy, the French-speaki ...
(to collaborate with Jean Piaget
Jean William Fritz Piaget (, , ; 9 August 1896 – 16 September 1980) was a Swiss psychologist known for his work on child development. Piaget's theory of cognitive development and epistemological view are together called " genetic epistemolog ...
at the International Centre for Genetic Epistemology) and later to the Université Lille Nord de France
The Community of Universities and Institutions (COMUE) Lille Nord de France (formerly Université Lille Nord de France) was a French Groups of Universities and Institutions ( COMUE) spread over multiple campuses and centered in Lille (North - Hauts ...
. In 1958 the couple moved to the United States where Mandelbrot joined the research staff at the IBM Thomas J. Watson Research Center
The Thomas J. Watson Research Center is the headquarters for IBM Research. The center comprises three sites, with its main laboratory in Yorktown Heights, New York, U.S., 38 miles (61 km) north of New York City, Albany, New York and wit ...
in Yorktown Heights, New York
Yorktown Heights is a census-designated place (CDP) in the administrative divisions of New York#Town, town of Yorktown, New York, Yorktown in Westchester County, New York, Westchester County, New York (state), New York, United States. The popula ...
. He remained at IBM for 35 years, becoming an IBM Fellow, and later Fellow Emeritus
''Emeritus'' (; female: ''emerita'') is an adjective used to designate a retired chair, professor, pastor, bishop, pope, director, president, prime minister, rabbi, emperor, or other person who has been "permitted to retain as an honorary title ...
.
From 1951 onward, Mandelbrot worked on problems and published papers not only in mathematics but in applied fields such as information theory
Information theory is the scientific study of the quantification (science), quantification, computer data storage, storage, and telecommunication, communication of information. The field was originally established by the works of Harry Nyquist a ...
, economics, and fluid dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids— liquids and gases. It has several subdisciplines, including ''aerodynamics'' (the study of air and other gases in motion) an ...
.
Randomness and fractals in financial markets
Mandelbrot sawfinancial market
A financial market is a market in which people trade financial securities and derivatives at low transaction costs. Some of the securities include stocks and bonds, raw materials and precious metals, which are known in the financial markets ...
s as an example of "wild randomness", characterized by concentration and long range dependence. He developed several original approaches for modelling financial fluctuations. In his early work, he found that the price changes in financial market
A financial market is a market in which people trade financial securities and derivatives at low transaction costs. Some of the securities include stocks and bonds, raw materials and precious metals, which are known in the financial markets ...
s did not follow a Gaussian distribution, but rather Lévy stable distributions
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be sta ...
having infinite variance
In probability theory and statistics, variance is the expectation of the squared deviation of a random variable from its population mean or sample mean. Variance is a measure of dispersion, meaning it is a measure of how far a set of numbers ...
. He found, for example, that cotton prices followed a Lévy stable distribution with parameter ''α'' equal to 1.7 rather than 2 as in a Gaussian distribution. "Stable" distributions have the property that the sum of many instances of a random variable follows the same distribution but with a larger scale parameter
In probability theory and statistics, a scale parameter is a special kind of numerical parameter of a parametric family of probability distributions. The larger the scale parameter, the more spread out the distribution.
Definition
If a family o ...
. The latter work from the early 60s was done with daily data of cotton prices from 1900, long before he introduced the word 'fractal'. In later years, after the concept of fractals had matured, the study of financial markets in the context of fractals became possible only after the availability of high frequency data in finance. In the late 1980s, Mandelbrot used intra-daily tick data supplied by Olsen & Associates in Zurich to apply fractal theory to market microstructure. This cooperation lead to the publication of the first comprehensive papers on scaling law in finance. This law shows similar properties at different time scales, confirming Mandelbrot's insight of the fractal nature of market microstructure. Mandelbrot's own research in this area is presented in his books ''Fractals and Scaling in Finance'' and ''The (Mis)behavior of Markets''.
Developing "fractal geometry" and the Mandelbrot set
As a visiting professor atHarvard University
Harvard University is a private Ivy League research university in Cambridge, Massachusetts. Founded in 1636 as Harvard College and named for its first benefactor, the Puritan clergyman John Harvard, it is the oldest institution of higher le ...
, Mandelbrot began to study mathematical objects called Julia set
In the context of complex dynamics, a branch of mathematics, the Julia set and the Fatou set are two complementary sets (Julia "laces" and Fatou "dusts") defined from a function. Informally, the Fatou set of the function consists of values wi ...
s that were invariant under certain transformations of the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the ...
. Building on previous work by Gaston Julia
Gaston Maurice Julia (3 February 1893 – 19 March 1978) was a French Algerian mathematician who devised the formula for the Julia set. His works were popularized by French mathematician Benoit Mandelbrot; the Julia and Mandelbrot fractals are ...
and Pierre Fatou
Pierre Joseph Louis Fatou (28 February 1878 – 9 August 1929) was a French mathematician and astronomer. He is known for major contributions to several branches of analysis. The Fatou lemma and the Fatou set are named after him.
Biography
P ...
, Mandelbrot used a computer to plot images of the Julia sets. While investigating the topology of these Julia sets, he studied the Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
which was introduced by him in 1979.
 In 1975, Mandelbrot coined the term ''
In 1975, Mandelbrot coined the term ''fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as illu ...
'' to describe these structures and first published his ideas in the French book ''Les Objets Fractals: Forme, Hasard et Dimension'', later translated in 1977 as ''Fractals: Form, Chance and Dimension''. According to computer scientist and physicist Stephen Wolfram
Stephen Wolfram (; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer science, mathematics, and theoretical physics. In 2012, he was named a fellow of the American Ma ...
, the book was a "breakthrough" for Mandelbrot, who until then would typically "apply fairly straightforward mathematics ... to areas that had barely seen the light of serious mathematics before". Wolfram adds that as a result of this new research, he was no longer a "wandering scientist", and later called him "the father of fractals":
Wolfram briefly describes fractals as a form of geometric repetition, "in which smaller and smaller copies of a pattern are successively nested inside each other, so that the same intricate shapes appear no matter how much you zoom in to the whole. Fern leaves and Romanesque broccoli are two examples from nature." He points out an unexpected conclusion:
Mandelbrot used the term "fractal" as it derived from the Latin word "fractus", defined as broken or shattered glass. Using the newly developed IBM computers at his disposal, Mandelbrot was able to create fractal images using graphics computer code, images that an interviewer described as looking like "the delirious exuberance of the 1960s psychedelic art
Psychedelic art (also known as psychedelia) is art, graphics or visual displays related to or inspired by psychedelic experiences and hallucinations known to follow the ingestion of psychedelic drugs such as LSD, psilocybin, and DMT. The word ...
with forms hauntingly reminiscent of nature and the human body". He also saw himself as a "would-be Kepler", after the 17th-century scientist Johannes Kepler
Johannes Kepler (; ; 27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws ...
, who calculated and described the orbits of the planets.
 Mandelbrot, however, never felt he was inventing a new idea. He described his feelings in a documentary with science writer Arthur C. Clarke:
According to Clarke, "the
Mandelbrot, however, never felt he was inventing a new idea. He described his feelings in a documentary with science writer Arthur C. Clarke:
According to Clarke, "the Mandelbrot set
The Mandelbrot set () is the set of complex numbers c for which the function f_c(z)=z^2+c does not diverge to infinity when iterated from z=0, i.e., for which the sequence f_c(0), f_c(f_c(0)), etc., remains bounded in absolute value.
This ...
is indeed one of the most astonishing discoveries in the entire history of mathematics. Who could have dreamed that such an incredibly simple equation could have generated images of literally ''infinite'' complexity?" Clarke also notes an "odd coincidencethe name Mandelbrot, and the word "In 1982, Mandelbrot expanded and updated his ideas in ''mandala A mandala ( sa, मण्डल, maṇḍala, circle, ) is a geometric configuration of symbols. In various spiritual traditions, mandalas may be employed for focusing attention of practitioners and adepts, as a spiritual guidance tool, for e ..."—for a religious symbol—which I'm sure is a pure coincidence, but indeed the Mandelbrot set does seem to contain an enormous number of mandalas.
The Fractal Geometry of Nature
''The Fractal Geometry of Nature'' is a 1982 book by the Franco-American mathematician Benoît Mandelbrot.
Overview
''The Fractal Geometry of Nature'' is a revised and enlarged version of his 1977 book entitled ''Fractals: Form, Chance and Dimen ...
''. This influential work brought fractals into the mainstream of professional and popular mathematics, as well as silencing critics, who had dismissed fractals as " program artifacts".
Mandelbrot left IBM in 1987, after 35 years and 12 days, when IBM decided to end pure research in his division. He joined the Department of Mathematics at Yale
Yale University is a private research university in New Haven, Connecticut. Established in 1701 as the Collegiate School, it is the third-oldest institution of higher education in the United States and among the most prestigious in the wor ...
, and obtained his first tenure
Tenure is a category of academic appointment existing in some countries. A tenured post is an indefinite academic appointment that can be terminated only for cause or under extraordinary circumstances, such as financial exigency or program disco ...
d post in 1999, at the age of 75. At the time of his retirement in 2005, he was Sterling Professor of Mathematical Sciences.
Fractals and the "theory of roughness"
Mandelbrot created the first-ever "theory of roughness", and he saw "roughness" in the shapes of mountains,coastline
The coast, also known as the coastline or seashore, is defined as the area where land meets the ocean, or as a line that forms the boundary between the land and the coastline. The Earth has around of coastline. Coasts are important zones in n ...
s and river basin
A drainage basin is an area of land where all flowing surface water converges to a single point, such as a river mouth, or flows into another body of water, such as a lake or ocean. A basin is separated from adjacent basins by a perimeter, the ...
s; the structures of plants, blood vessel
The blood vessels are the components of the circulatory system that transport blood throughout the human body. These vessels transport blood cells, nutrients, and oxygen to the tissues of the body. They also take waste and carbon dioxide away ...
s and lung
The lungs are the primary organs of the respiratory system in humans and most other animals, including some snails and a small number of fish. In mammals and most other vertebrates, two lungs are located near the backbone on either side of t ...
s; the clustering of galaxies. His personal quest was to create some mathematical formula to measure the overall "roughness" of such objects in nature. He began by asking himself various kinds of questions related to nature:
In his paper "How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension
"How Long Is the Coast of Britain? Statistical Self-Similarity and Fractional Dimension" is a paper by mathematician Benoit Mandelbrot, first published in ''Science'' on 5 May 1967. In this paper, Mandelbrot discusses self-similar curves that ...
", published in ''Science'' in 1967, Mandelbrot discusses self-similar curves that have Hausdorff dimension
In mathematics, Hausdorff dimension is a measure of ''roughness'', or more specifically, fractal dimension, that was first introduced in 1918 by mathematician Felix Hausdorff. For instance, the Hausdorff dimension of a single point is zero, of ...
that are examples of ''fractals'', although Mandelbrot does not use this term in the paper, as he did not coin it until 1975. The paper is one of Mandelbrot's first publications on the topic of fractals.
Mandelbrot emphasized the use of fractals as realistic and useful models for describing many "rough" phenomena in the real world. He concluded that "real roughness is often fractal and can be measured." Although Mandelbrot coined the term "fractal", some of the mathematical objects he presented in ''The Fractal Geometry of Nature
''The Fractal Geometry of Nature'' is a 1982 book by the Franco-American mathematician Benoît Mandelbrot.
Overview
''The Fractal Geometry of Nature'' is a revised and enlarged version of his 1977 book entitled ''Fractals: Form, Chance and Dimen ...
'' had been previously described by other mathematicians. Before Mandelbrot, however, they were regarded as isolated curiosities with unnatural and non-intuitive properties. Mandelbrot brought these objects together for the first time and turned them into essential tools for the long-stalled effort to extend the scope of science to explaining non-smooth, "rough" objects in the real world. His methods of research were both old and new:
Fractals are also found in human pursuits, such as music, painting, architecture, and stock market
A stock market, equity market, or share market is the aggregation of buyers and sellers of stocks (also called shares), which represent ownership claims on businesses; these may include ''securities'' listed on a public stock exchange, as ...
prices. Mandelbrot believed that fractals, far from being unnatural, were in many ways more intuitive and natural than the artificially smooth objects of traditional Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
: Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line.
—Mandelbrot, in his introduction to ''The Fractal Geometry of Nature''
 Mandelbrot has been called an artist, and a visionary and a maverick. His informal and passionate style of writing and his emphasis on visual and geometric intuition (supported by the inclusion of numerous illustrations) made ''The Fractal Geometry of Nature'' accessible to non-specialists. The book sparked widespread popular interest in fractals and contributed to chaos theory and other fields of science and mathematics.
Mandelbrot also put his ideas to work in cosmology. He offered in 1974 a new explanation of
Mandelbrot has been called an artist, and a visionary and a maverick. His informal and passionate style of writing and his emphasis on visual and geometric intuition (supported by the inclusion of numerous illustrations) made ''The Fractal Geometry of Nature'' accessible to non-specialists. The book sparked widespread popular interest in fractals and contributed to chaos theory and other fields of science and mathematics.
Mandelbrot also put his ideas to work in cosmology. He offered in 1974 a new explanation of Olbers' paradox
Olbers's paradox, also known as the dark night sky paradox, is an argument in astrophysics and physical cosmology that says that the darkness of the night sky conflicts with the assumption of an infinite and eternal static universe. In the hyp ...
(the "dark night sky" riddle), demonstrating the consequences of fractal theory as a sufficient, but not necessary, resolution of the paradox. He postulated that if the star
A star is an astronomical object comprising a luminous spheroid of plasma (physics), plasma held together by its gravity. The List of nearest stars and brown dwarfs, nearest star to Earth is the Sun. Many other stars are visible to the naked ...
s in the universe were fractally distributed (for example, like Cantor dust
In mathematics, the Cantor set is a set of points lying on a single line segment that has a number of unintuitive properties. It was discovered in 1874 by Henry John Stephen Smith and introduced by German mathematician Georg Cantor in 1883.
...
), it would not be necessary to rely on the Big Bang
The Big Bang event is a physical theory that describes how the universe expanded from an initial state of high density and temperature. Various cosmological models of the Big Bang explain the evolution of the observable universe from the ...
theory to explain the paradox. His model would not rule out a Big Bang, but would allow for a dark sky even if the Big Bang had not occurred.
Awards and honors
Mandelbrot's awards include theWolf Prize
The Wolf Prize is an international award granted in Israel, that has been presented most years since 1978 to living scientists and artists for ''"achievements in the interest of mankind and friendly relations among people ... irrespective of natio ...
for Physics in 1993, the Lewis Fry Richardson Prize of the European Geophysical Society
The European Geosciences Union (EGU) is a non-profit international union in the fields of Earth, planetary, and space sciences whose vision is to "realise a sustainable and just future for humanity and for the planet." The organisation has headq ...
in 2000, the Japan Prize in 2003,Laureates of the Japan Prize. japanprize.jp and the Einstein Lectureship of the
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, ...
in 2006.
The small asteroid 27500 Mandelbrot was named in his honor. In November 1990, he was made a Chevalier in France's Legion of Honour
The National Order of the Legion of Honour (french: Ordre national de la Légion d'honneur), formerly the Royal Order of the Legion of Honour ('), is the highest French order of merit, both military and civil. Established in 1802 by Napoleon, ...
. In December 2005, Mandelbrot was appointed to the position of Battelle Fellow at the Pacific Northwest National Laboratory
Pacific Northwest National Laboratory (PNNL) is one of the United States Department of Energy national laboratories, managed by the Department of Energy's (DOE) Office of Science. The main campus of the laboratory is in Richland, Washington.
O ...
. Mandelbrot was promoted to an Officer of the Legion of Honour in January 2006. An honorary degree from Johns Hopkins University
Johns Hopkins University (Johns Hopkins, Hopkins, or JHU) is a private university, private research university in Baltimore, Maryland. Founded in 1876, Johns Hopkins is the oldest research university in the United States and in the western hem ...
was bestowed on Mandelbrot in the May 2010 commencement exercises.
A partial list of awards received by Mandelbrot:
* 2004 Best Business Book of the Year Award
* AMS Einstein Lectureship
* Barnard Medal
* Caltech Service
* Casimir Funk
Kazimierz Funk (; February 23, 1884 – November 19, 1967), commonly anglicized as Casimir Funk, was a Polish-American biochemist generally credited with being among the first to formulate (in 1912) the concept of vitamins, which he called "vit ...
Natural Sciences Award
* Charles Proteus Steinmetz
Charles Proteus Steinmetz (born Karl August Rudolph Steinmetz, April 9, 1865 – October 26, 1923) was a German-born American mathematician and electrical engineer and professor at Union College. He fostered the development of alternati ...
Medal
* High School Spelling Bee (1940)
* Fellow, American Geophysical Union
* Fellow of the American Statistical Association
Like many other academic professional societies, the American Statistical Association (ASA) uses the title of Fellow of the American Statistical Association as its highest honorary grade of membership. The number of new fellows per year is limited ...
* Fellow of the American Physical Society (1987)
* Franklin Medal
The Franklin Medal was a science award presented from 1915 until 1997 by the Franklin Institute
The Franklin Institute is a science museum and the center of science education and research in Philadelphia, Pennsylvania. It is named after the Am ...
* Harvey Prize
Harvey Prize is an annual Israeli award for breakthroughs in science and technology, as well as contributions to peace in the Middle East granted by the Technion in Haifa.
History
The prize is named for industrialist and inventor Leo Harvey. T ...
(1989)
* Honda Prize
* Humboldtpreis
* IBM Fellowship
* Japan Prize (2003)
* John Scott Award
John Scott Award, created in 1816 as the John Scott Legacy Medal and Premium, is presented to men and women whose inventions improved the "comfort, welfare, and happiness of human kind" in a significant way. "...the John Scott Medal Fund, establish ...
* Légion d'honneur (Legion of Honour
The National Order of the Legion of Honour (french: Ordre national de la Légion d'honneur), formerly the Royal Order of the Legion of Honour ('), is the highest French order of merit, both military and civil. Established in 1802 by Napoleon, ...
)
* Lewis Fry Richardson Medal
* Medaglia della Presidenza della Repubblica Italiana
* Médaille de Vermeil de la Ville de Paris
* Nevada Prize
* Member of the Norwegian Academy of Science and Letters
The Norwegian Academy of Science and Letters ( no, Det Norske Videnskaps-Akademi, DNVA) is a learned society based in Oslo, Norway. Its purpose is to support the advancement of science and scholarship in Norway.
History
The Royal Frederick Unive ...
.
* Member of the American Philosophical Society
The American Philosophical Society (APS), founded in 1743 in Philadelphia, is a scholarly organization that promotes knowledge in the sciences and humanities through research, professional meetings, publications, library resources, and communit ...
(2004)
* Science for Art
* Sven Berggren-Priset
* Władysław Orlicz Prize
* Wolf Foundation Prize for Physics (1993)
Death and legacy
Mandelbrot died frompancreatic cancer
Pancreatic cancer arises when cell (biology), cells in the pancreas, a glandular organ behind the stomach, begin to multiply out of control and form a Neoplasm, mass. These cancerous cells have the malignant, ability to invade other parts of t ...
at the age of 85 in a hospice
Hospice care is a type of health care that focuses on the palliation of a terminally ill patient's pain and symptoms and attending to their emotional and spiritual needs at the end of life. Hospice care prioritizes comfort and quality of life by ...
in Cambridge, Massachusetts
Cambridge ( ) is a city in Middlesex County, Massachusetts, United States. As part of the Boston metropolitan area, the cities population of the 2020 U.S. census was 118,403, making it the fourth most populous city in the state, behind Boston, ...
on 14 October 2010. Reacting to news of his death, mathematician Heinz-Otto Peitgen
Heinz-Otto Peitgen (born April 30, 1945 in Bruch, Nümbrecht near Cologne) is a German mathematician and was President of Jacobs University from January 1, 2013 to December 31, 2013. Peitgen contributed to the study of fractals, chaos theory, an ...
said: " we talk about impact inside mathematics, and applications in the sciences, he is one of the most important figures of the last fifty years."
Chris Anderson Chris Anderson may refer to:
Sports
* Chris Anderson (baseball) (born 1992), American baseball player
* Chris Anderson (cheese roller), 22-time winner of annual cheese rolling
* Chris Anderson (footballer, born 1925) (1925–1986), Scottish footb ...
, TED conference
TED Conferences, LLC (Technology, Entertainment, Design) is an American-Canadian non-profit media organization that posts international talks online for free distribution under the slogan "ideas worth spreading". TED was founded by Richard Sau ...
curator, described Mandelbrot as "an icon who changed how we see the world". Nicolas Sarkozy
Nicolas Paul Stéphane Sarközy de Nagy-Bocsa (; ; born 28 January 1955) is a French politician who served as President of France from 2007 to 2012.
Born in Paris, he is of Hungarian, Greek Jewish, and French origin. Mayor of Neuilly-sur-Se ...
, President of France
The president of France, officially the president of the French Republic (french: Président de la République française), is the executive head of state of France, and the commander-in-chief of the French Armed Forces. As the presidency i ...
at the time of Mandelbrot's death, said Mandelbrot had "a powerful, original mind that never shied away from innovating and shattering preconceived notions .. hs work, developed entirely outside mainstream research, led to modern information theory." Mandelbrot's obituary in ''The Economist'' points out his fame as "celebrity beyond the academy" and lauds him as the "father of fractal geometry".. ''The Economist'' (21 October 2010) Best-selling essayist-author
Nassim Nicholas Taleb
Nassim Nicholas Taleb (; alternatively ''Nessim ''or'' Nissim''; born 12 September 1960) is a Lebanese-American essayist, mathematical statistician, former option trader, risk analyst, and aphorist whose work concerns problems of randomness, ...
has remarked that Mandelbrot's book ''The (Mis)Behavior of Markets'' is in his opinion "The deepest and most realistic finance book ever published".
Bibliography
In English
* ''Fractals: Form, Chance and Dimension'', 1977, 2020 * ''The Fractal Geometry of Nature
''The Fractal Geometry of Nature'' is a 1982 book by the Franco-American mathematician Benoît Mandelbrot.
Overview
''The Fractal Geometry of Nature'' is a revised and enlarged version of his 1977 book entitled ''Fractals: Form, Chance and Dimen ...
'', 1982
*
* Mandelbrot, B. (1959) Variables et processus stochastiques de Pareto-Levy, et la repartition des revenus. Comptes rendus de l'Académie des Sciences de Paris, 249, 613–615.
* Mandelbrot, B. (1960) The Pareto-Levy law and the distribution of income. International Economic Review, 1, 79–106.
* Mandelbrot, B. (1961) Stable Paretian random functions and the multiplicative variation of income. Econometrica, 29, 517–543.
* Mandelbrot, B. (1964) Random walks, fire damage amount and other Paretian risk phenomena. Operations Research, 12, 582–585.
* ''Fractals and Scaling in Finance: Discontinuity, Concentration, Risk. Selecta Volume E'', 1997 by Benoit B. Mandelbrot and R.E. Gomory
* Mandelbrot, Benoit B. (1997) ''Fractals and Scaling in Finance: Discontinuity, Concentration, Risk'', Springer.
* ''Fractales, hasard et finance'', 1959–1997, 1 November 1998
* ''Multifractals and 1/ƒ Noise: Wild Self-Affinity in Physics (1963–1976)'' (Selecta; V.N) 18 January 1999 by J.M. Berger and Benoit B. Mandelbrot
*
* ''Gaussian Self-Affinity and Fractals: Globality, The Earth, 1/f Noise, and R/S (Selected Works of Benoit B. Mandelbrot)'' 14 December 2001 by Benoit Mandelbrot and F.J. Damerau
* Mandelbrot, Benoit B., ''Gaussian Self-Affinity and Fractals'', Springer: 2002.
* ''Fractals and Chaos: The Mandelbrot Set and Beyond'', 9 January 2004
* ''The Misbehavior of Markets: A Fractal View of Financial Turbulence'', 2006 by Benoit Mandelbrot and Richard L. Hudson
* Mandelbrot, Benoit B. (2010)''The Fractalist, Memoir of a Scientific Maverick.''
New York
Vintage Books
Division of Random House. * ''The Fractalist: Memoir of a Scientific Maverick'', 2014 * *
Heinz-Otto Peitgen
Heinz-Otto Peitgen (born April 30, 1945 in Bruch, Nümbrecht near Cologne) is a German mathematician and was President of Jacobs University from January 1, 2013 to December 31, 2013. Peitgen contributed to the study of fractals, chaos theory, an ...
, Hartmut Jürgens, Dietmar Saupe and Cornelia Zahlten: ''Fractals: An Animated Discussion'' (63 min video film, interviews with Benoît Mandelbrot and Edward Lorenz, computer animations), W.H. Freeman and Company, 1990. (re-published by Films for the Humanities & Sciences, )
*
"Hunting the Hidden Dimension: mysteriously beautiful fractals are shaking up the world of mathematics and deepening our understanding of nature"
''
NOVA
A nova (plural novae or novas) is a transient astronomical event that causes the sudden appearance of a bright, apparently "new" star (hence the name "nova", which is Latin for "new") that slowly fades over weeks or months. Causes of the dramati ...
'', WGBH Educational Foundation, Boston for PBS, first aired 28 October 2008.
See also
Notes
References
Sources
*External links
*Mandelbrot's page at Yale
(TED address).
Fractals in Science, Engineering and Finance
(lecture).
FT.com interview
on the subject of the financial markets which includes his critique of the "efficient market" hypothesis. *
Mandelbrot relates his life story
(
Web of Stories
Web of Stories is an online collection of thousands of autobiographical video-stories. Web of Stories, originally known as Science Archive, was set up to record the life stories of scientists. When it expanded to include the lives of authors, mov ...
).
Interview (1 January 1981, Ithaca, NY)
held by the
Eugene Dynkin
Eugene Borisovich Dynkin (russian: link=no, Евгений Борисович Дынкин; 11 May 1924 – 14 November 2014) was a Soviet and American mathematician. He made contributions to the fields of probability and algebra, especially sem ...
Collection of Mathematics Interviews, Cornell University Library
The Cornell University Library is the library system of Cornell University. As of 2014, it holds over 8 million printed volumes and over a million ebooks. More than 90 percent of its current 120,000 Periodical literature, periodical titles are ...
.
Video animation of Mandelbrot set
zoom factor 10342. * , a three-dimensional Mandelbrot-set projection. * * *
Michael Frame, "Benoit B. Mandelbrot", Biographical Memoirs of the National Academy of Sciences (2014)
{{DEFAULTSORT:Mandelbrot, Benoit 1924 births 2010 deaths 20th-century American economists 20th-century American mathematicians 20th-century French mathematicians 21st-century American economists 21st-century American mathematicians 21st-century French mathematicians California Institute of Technology alumni Chaos theorists Deaths from cancer in Massachusetts Deaths from pancreatic cancer École Polytechnique alumni Fellows of the American Geophysical Union Fellows of the American Physical Society Fellows of the American Statistical Association Fellows of the Econometric Society French emigrants to the United States Harvard University people IBM Fellows IBM Research computer scientists IBM employees Institute for Advanced Study visiting scholars Jewish French scientists Members of the Norwegian Academy of Science and Letters Members of the United States National Academy of Sciences Officiers of the Légion d'honneur 20th-century Polish Jews Polish emigrants to France Polish people of Lithuanian descent University of Paris alumni Wolf Prize in Physics laureates Yale Sterling Professors Yale University faculty Members of the American Philosophical Society