|
Production (computer Science)
In computer science, a production or production rule is a rewrite rule that replaces some symbols with other symbols. A finite set of productions P is the main component in the specification of a formal grammar (specifically a generative grammar). The other components are a finite set N of nonterminal symbols, a finite set (known as an alphabet) \Sigma of terminal symbols that is disjoint from N and a distinguished symbol S \in N that is the ''start symbol''. In an unrestricted grammar, a production is of the form u \to v, where u and v are arbitrary strings of terminals and nonterminals, and u may not be the empty string. If v is the empty string, this is denoted by the symbol \epsilon, or \lambda (rather than leaving the right-hand side blank). So productions are members of the cartesian product :V^*NV^* \times V^* = (V^*\setminus\Sigma^*) \times V^*, where V := N \cup \Sigma is the ''vocabulary'', ^ is the Kleene star operator, V^*NV^* indicates concatenation, \cup deno ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chomsky Hierarchy
The Chomsky hierarchy in the fields of formal language theory, computer science, and linguistics, is a containment hierarchy of classes of formal grammars. A formal grammar describes how to form strings from a formal language's alphabet that are valid according to the language's syntax. The linguist Noam Chomsky theorized that four different classes of formal grammars existed that could generate increasingly complex languages. Each class can also completely generate the language of all inferior classes (set inclusive). History The general idea of a hierarchy of grammars was first described by Noam Chomsky in "Three models for the description of language" during the formalization of transformational-generative grammar (TGG). Marcel-Paul Schützenberger also played a role in the development of the theory of formal languages; the paper "The algebraic theory of context free languages" describes the modern hierarchy, including context-free grammars. Independently, alongside linguis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Grammar
In linguistics, grammar is the set of rules for how a natural language is structured, as demonstrated by its speakers or writers. Grammar rules may concern the use of clauses, phrases, and words. The term may also refer to the study of such rules, a subject that includes phonology, morphology (linguistics), morphology, and syntax, together with phonetics, semantics, and pragmatics. There are, broadly speaking, two different ways to study grammar: traditional grammar and #Theoretical frameworks, theoretical grammar. Fluency in a particular language variety involves a speaker internalizing these rules, many or most of which are language acquisition, acquired by observing other speakers, as opposed to intentional study or language teaching, instruction. Much of this internalization occurs during early childhood; learning a language later in life usually involves more direct instruction. The term ''grammar'' can also describe the linguistic behaviour of groups of speakers and writer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Post Canonical System
A Post canonical system, also known as a Post production system, as created by Emil Post, is a string-manipulation system that starts with finitely many strings and repeatedly transforms them by applying a finite set j of specified rules of a certain form, thus generating a formal language. Today they are mainly of historical relevance because every Post canonical system can be reduced to a string rewriting system (semi-Thue system), which is a simpler formulation. Both formalisms are Turing complete. Definition A Post canonical system is a triplet (A,I,R), where * A is a finite alphabet, and finite (possibly empty) strings on A are called ''words''. * I is a finite set of ''initial words''. * R is a finite set of string-transforming rules (called '' production rules''), each rule being of the following form: : \overset where each and is a specified fixed word, and each ''$'' and ''$' '' is a variable standing for an arbitrary word. The strings before and after the arrow ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
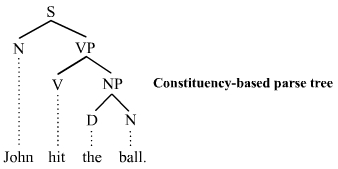
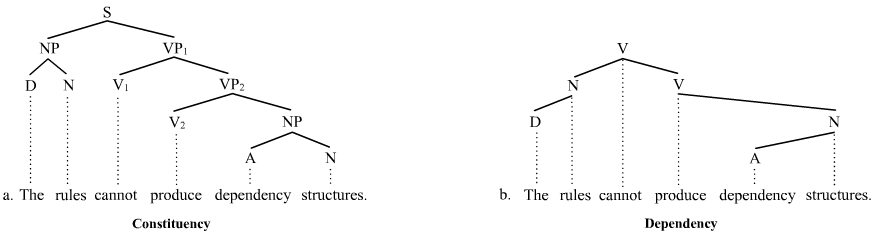
Phrase Structure Rule
Phrase structure rules are a type of rewrite rule used to describe a given language's syntax and are closely associated with the early stages of transformational grammar, proposed by Noam Chomsky in 1957. They are used to break down a natural language sentence into its constituent parts, also known as syntactic category, syntactic categories, including both lexical categories (part of speech, parts of speech) and phrase, phrasal categories. A grammar that uses phrase structure rules is a type of phrase structure grammar. Phrase structure rules as they are commonly employed operate according to the constituent (linguistics), constituency relation, and a grammar that employs phrase structure rules is therefore a phrase structure grammar, ''constituency grammar''; as such, it stands in contrast to dependency grammar, ''dependency grammars'', which are based on the government (linguistics), dependency relation. Definition and examples Phrase structure rules are usually of the following ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Backus–Naur Form
In computer science, Backus–Naur form (BNF, pronounced ), also known as Backus normal form, is a notation system for defining the Syntax (programming languages), syntax of Programming language, programming languages and other Formal language, formal languages, developed by John Backus and Peter Naur. It is a metasyntax for Context-free grammar, context-free grammars, providing a precise way to outline the rules of a language's structure. It has been widely used in official specifications, manuals, and textbooks on programming language theory, as well as to describe Document format, document formats, Instruction set, instruction sets, and Communication protocol, communication protocols. Over time, variations such as extended Backus–Naur form (EBNF) and augmented Backus–Naur form (ABNF) have emerged, building on the original framework with added features. Structure BNF specifications outline how symbols are combined to form syntactically valid sequences. Each BNF consists of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rewrite Rule
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a well-formed formula, formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus Relation (mathematics), relations on how to transform those objects. Rewriting can be non-deterministic algorithm, non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several automated theorem proving, theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
L-system
An L-system or Lindenmayer system is a parallel rewriting system and a type of formal grammar. An L-system consists of an alphabet of symbols that can be used to make strings, a collection of production rules that expand each symbol into some larger string of symbols, an initial "axiom" string from which to begin construction, and a mechanism for translating the generated strings into geometric structures. L-systems were introduced and developed in 1968 by Aristid Lindenmayer, a Hungarian theoretical biologist and botanist at the University of Utrecht. Lindenmayer used L-systems to describe the behaviour of plant cells and to model the growth processes of plant development. L-systems have also been used to model the morphology of a variety of organisms and can be used to generate self-similar fractals. Origins As a biologist, Lindenmayer worked with yeast and filamentous fungi and studied the growth patterns of various types of bacteria, such as the cyanobacteria '' Anabaena ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generative Grammar
Generative grammar is a research tradition in linguistics that aims to explain the cognitive basis of language by formulating and testing explicit models of humans' subconscious grammatical knowledge. Generative linguists, or generativists (), tend to share certain working assumptions such as the competence–performance distinction and the notion that some domain-specific aspects of grammar are partly innate in humans. These assumptions are rejected in non-generative approaches such as usage-based models of language. Generative linguistics includes work in core areas such as syntax, semantics, phonology, psycholinguistics, and language acquisition, with additional extensions to topics including biolinguistics and music cognition. Generative grammar began in the late 1950s with the work of Noam Chomsky, having roots in earlier approaches such as structural linguistics. The earliest version of Chomsky's model was called Transformational grammar, with subsequent itera ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Automata
A finite-state machine (FSM) or finite-state automaton (FSA, plural: ''automata''), finite automaton, or simply a state machine, is a mathematical model of computation. It is an abstract machine that can be in exactly one of a finite number of '' states'' at any given time. The FSM can change from one state to another in response to some inputs; the change from one state to another is called a ''transition''. An FSM is defined by a list of its states, its initial state, and the inputs that trigger each transition. Finite-state machines are of two types— deterministic finite-state machines and non-deterministic finite-state machines. For any non-deterministic finite-state machine, an equivalent deterministic one can be constructed. The behavior of state machines can be observed in many devices in modern society that perform a predetermined sequence of actions depending on a sequence of events with which they are presented. Simple examples are: vending machines, which dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Grammar
A formal grammar is a set of Terminal and nonterminal symbols, symbols and the Production (computer science), production rules for rewriting some of them into every possible string of a formal language over an Alphabet (formal languages), alphabet. A grammar does not describe the semantics, meaning of the strings — only their form. In applied mathematics, formal language theory is the discipline that studies formal grammars and languages. Its applications are found in theoretical computer science, theoretical linguistics, Formal semantics (logic), formal semantics, mathematical logic, and other areas. A formal grammar is a Set_(mathematics), set of rules for rewriting strings, along with a "start symbol" from which rewriting starts. Therefore, a grammar is usually thought of as a language generator. However, it can also sometimes be used as the basis for a "recognizer"—a function in computing that determines whether a given string belongs to the language or is grammatical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ambiguous Grammar
In computer science, an ambiguous grammar is a context-free grammar for which there exists a string (computer science), string that can have more than one leftmost derivation or parse tree. Every non-empty context-free language admits an ambiguous grammar by introducing e.g. a duplicate rule. A language that only admits ambiguous grammars is called an #Inherently ambiguous languages, inherently ambiguous language. Deterministic context-free grammars are always unambiguous, and are an important subclass of unambiguous grammars; there are non-deterministic unambiguous grammars, however. For computer programming languages, the reference grammar is often ambiguous, due to issues such as the dangling else problem. If present, these ambiguities are generally resolved by adding precedence rules or other context-sensitive grammar, context-sensitive parsing rules, so the overall phrase grammar is unambiguous. Some parsing algorithms (such as Earley parser, Earley or Generalized LR parser, GL ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |