|
Isenthalpic Process
An isenthalpic process or isoenthalpic process is a process that proceeds without any change in enthalpy, ''H''; or specific enthalpy, ''h''. Overview If a steady-state, steady-flow process is analysed using a control volume, everything outside the control volume is considered to be the ''surroundings''.G. J. Van Wylen and R. E. Sonntag, ''Fundamentals of Classical Thermodynamics'', Section 2.1 (3rd edition). Such a process will be isenthalpic if there is no transfer of heat to or from the surroundings, no work done on or by the surroundings, and no change in the kinetic energy of the fluid.G. J. Van Wylen and R. E. Sonntag, ''Fundamentals of Classical Thermodynamics'', Section 5.13 (3rd edition). This is a sufficient but not necessary condition for isoenthalpy. The necessary condition for a process to be isoenthalpic is that the sum of each of the terms of the energy balance other than enthalpy (work, heat, changes in kinetic energy, etc.) cancel each other, so that the enthalpy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic System
A thermodynamic system is a body of matter and/or radiation separate from its surroundings that can be studied using the laws of thermodynamics. Thermodynamic systems can be passive and active according to internal processes. According to internal processes, passive systems and active systems are distinguished: passive, in which there is a redistribution of available energy, active, in which one type of energy is converted into another. Depending on its interaction with the environment, a thermodynamic system may be an isolated system, a Closed system#In thermodynamics, closed system, or an Open system (systems theory), open system. An isolated system does not exchange matter or energy with its surroundings. A closed system may exchange heat, experience forces, and exert forces, but does not exchange matter. An open system can interact with its surroundings by exchanging both matter and energy. The physical condition of a thermodynamic system at a given time is described by its ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Enthalpy
Enthalpy () is the sum of a thermodynamic system's internal energy and the product of its pressure and volume. It is a state function in thermodynamics used in many measurements in chemical, biological, and physical systems at a constant external pressure, which is conveniently provided by the large ambient atmosphere. The pressure–volume term expresses the work (physics), work W that was done against constant external pressure P_\text to establish the system's physical dimensions from V_\text=0 to some final volume V_\text (as W=P_\text\Delta V), i.e. to make room for it by displacing its surroundings. The pressure-volume term is very small for solids and liquids at common conditions, and fairly small for gases. Therefore, enthalpy is a stand-in for energy in chemical systems; Bond energy, bond, Lattice energy, lattice, solvation, and other chemical "energies" are actually enthalpy differences. As a state function, enthalpy depends only on the final configuration of internal e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Volume
In continuum mechanics and thermodynamics, a control volume (CV) is a mathematical abstraction employed in the process of creating mathematical models of physical processes. In an inertial frame of reference, it is a fictitious region of a given volume fixed in space or moving with constant flow velocity through which the ''continuuum'' (a continuous medium such as gas, liquid or solid) flows. The closed surface enclosing the region is referred to as the control surface. At steady state, a control volume can be thought of as an arbitrary volume in which the mass of the continuum remains constant. As a continuum moves through the control volume, the mass entering the control volume is equal to the mass leaving the control volume. At steady state, and in the absence of work and heat transfer, the energy within the control volume remains constant. It is analogous to the classical mechanics concept of the free body diagram. Overview Typically, to understand how a given physi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
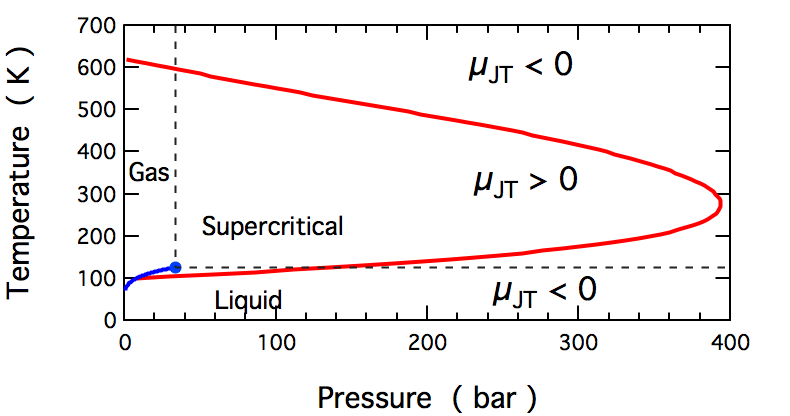
Joule–Thomson Effect
In thermodynamics, the Joule–Thomson effect (also known as the Joule–Kelvin effect or Kelvin–Joule effect) describes the temperature change of a Real gas, ''real'' gas or liquid (as differentiated from an ideal gas) when it is expanding; typically caused by the pressure loss from flow through a expansion valve (steam engine), valve or enthalpy#Throttling, porous plug while keeping it insulated so that Adiabatic process, no heat is exchanged with the environment. This procedure is called a ''throttling process'' or ''Joule–Thomson process''. The effect is purely due to deviation from ideality, as any ideal gas has no JT effect. At room temperature, all gases except hydrogen, helium, and neon cool upon expansion by the Joule–Thomson process when being throttled through an orifice; these three gases rise in temperature when forced through a porous plug at room temperature, but lowers in temperature when already at lower temperatures. Most liquids such as Hydraulics, hydr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics. The requirement of zero interaction can often be relaxed if, for example, the interaction is perfectly elastic or regarded as point-like collisions. Under various conditions of temperature and pressure, many real gases behave qualitatively like an ideal gas where the gas molecules (or atoms for monatomic gas) play the role of the ideal particles. Many gases such as nitrogen, oxygen, hydrogen, noble gases, some heavier gases like carbon dioxide and mixtures such as air, can be treated as ideal gases within reasonable tolerances over a considerable parameter range around standard temperature and pressure. Generally, a gas behaves more like an ideal gas at higher temperature and lower ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isothermal Process
An isothermal process is a type of thermodynamic process in which the temperature ''T'' of a system remains constant: Δ''T'' = 0. This typically occurs when a system is in contact with an outside thermal reservoir, and a change in the system occurs slowly enough to allow the system to be continuously adjusted to the temperature of the reservoir through heat exchange (see quasi-equilibrium). In contrast, an '' adiabatic process'' is where a system exchanges no heat with its surroundings (''Q'' = 0). Simply, we can say that in an isothermal process * T = \text * \Delta T = 0 * dT = 0 * For ideal gases only, internal energy \Delta U = 0 while in adiabatic processes: * Q = 0. Etymology The noun '' isotherm'' is derived from the Ancient Greek words (), meaning "equal", and (), meaning "heat". Examples Isothermal processes can occur in any kind of system that has some means of regulating the temperature, including highly structured machines, and even living ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Adiabatic Process
An adiabatic process (''adiabatic'' ) is a type of thermodynamic process that occurs without transferring heat between the thermodynamic system and its Environment (systems), environment. Unlike an isothermal process, an adiabatic process transfers energy to the surroundings only as Work (thermodynamics), work and/or mass flow.. A translation may be founhere. Also a mostly reliabltranslation is to be foundin As a key concept in thermodynamics, the adiabatic process supports the theory that explains the first law of thermodynamics. The opposite term to "adiabatic" is ''diabatic''. Some chemical and physical processes occur too rapidly for energy to enter or leave the system as heat, allowing a convenient "adiabatic approximation".Bailyn, M. (1994), pp. 52–53. For example, the adiabatic flame temperature uses this approximation to calculate the upper limit of fire, flame temperature by assuming combustion loses no heat to its surroundings. In meteorology, adiabatic expansion an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ideal Gas Laws
The ideal gas law, also called the general gas equation, is the equation of state of a hypothetical ideal gas. It is a good approximation of the behavior of many gases under many conditions, although it has several limitations. It was first stated by Benoît Paul Émile Clapeyron in 1834 as a combination of the empirical Boyle's law, Charles's law, Avogadro's law, and Gay-Lussac's law. The ideal gas law is often written in an empirical form: pV = nRT where p, V and T are the pressure, volume and temperature respectively; n is the amount of substance; and R is the ideal gas constant. It can also be derived from the microscopic kinetic theory, as was achieved (independently) by August Krönig in 1856 and Rudolf Clausius in 1857. Equation The state of an amount of gas is determined by its pressure, volume, and temperature. The modern form of the equation relates these simply in two main forms. The temperature used in the equation of state is an absolute temperature: the ap ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
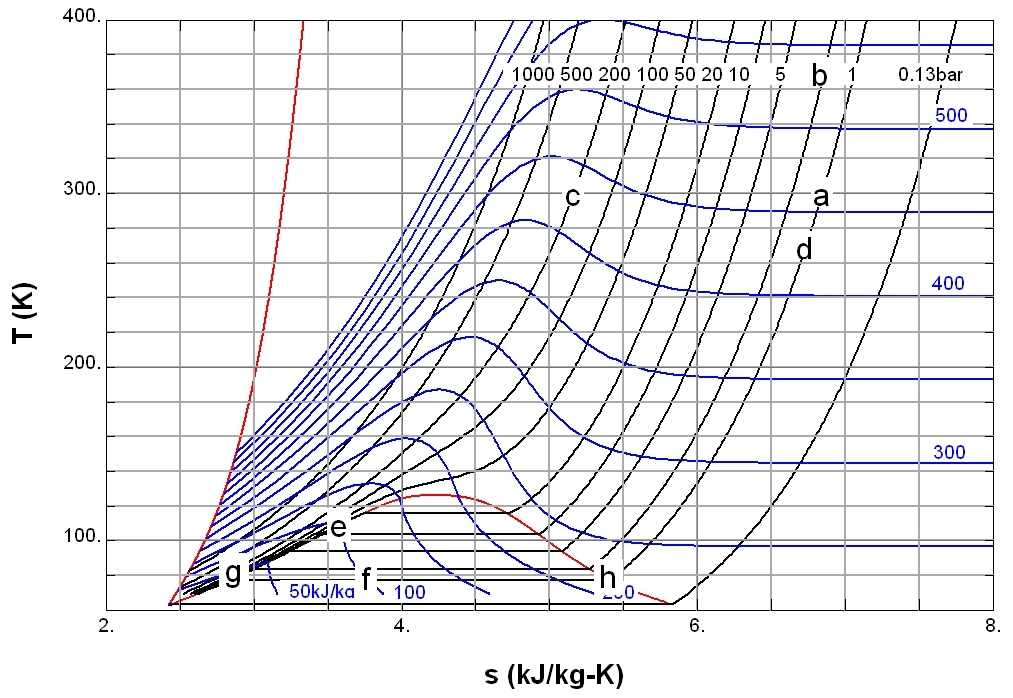
Isentropic Process
An isentropic process is an idealized thermodynamic process that is both Adiabatic process, adiabatic and Reversible process (thermodynamics), reversible. The work (physics), work transfers of the system are friction, frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamics, Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" derives from the proc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermodynamic Processes
Classical thermodynamics considers three main kinds of thermodynamic processes: (1) changes in a system, (2) cycles in a system, and (3) flow processes. (1) A Thermodynamic process is a process in which the thermodynamic state of a system is changed. A change in a system is defined by a passage from an initial to a final state of thermodynamic equilibrium. In classical thermodynamics, the actual course of the process is not the primary concern, and often is ignored. A state of thermodynamic equilibrium endures unchangingly unless it is interrupted by a thermodynamic operation that initiates a thermodynamic process. The equilibrium states are each respectively fully specified by a suitable set of thermodynamic state variables, that depend only on the current state of the system, not on the path taken by the processes that produce the state. In general, during the actual course of a thermodynamic process, the system may pass through physical states which are not describable as th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |