|
Epitrochoid
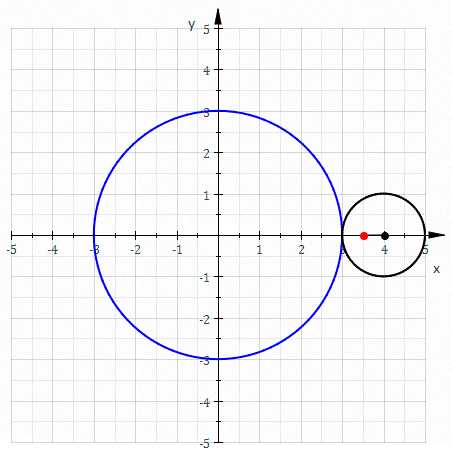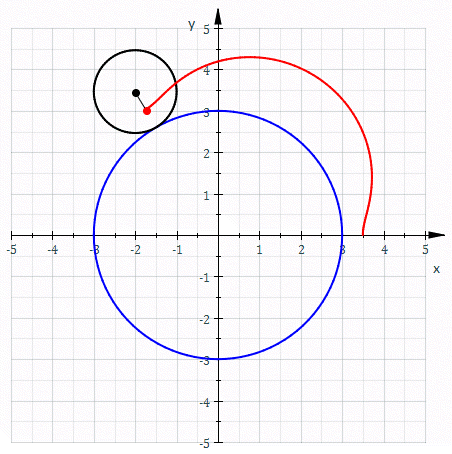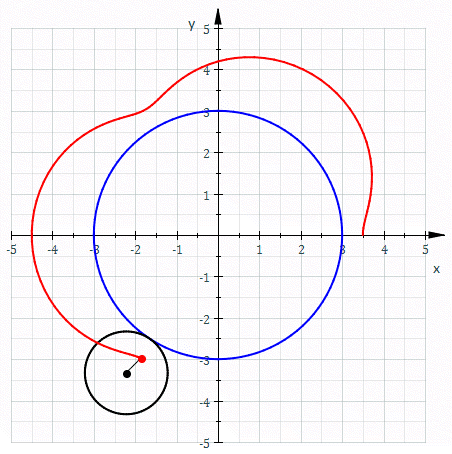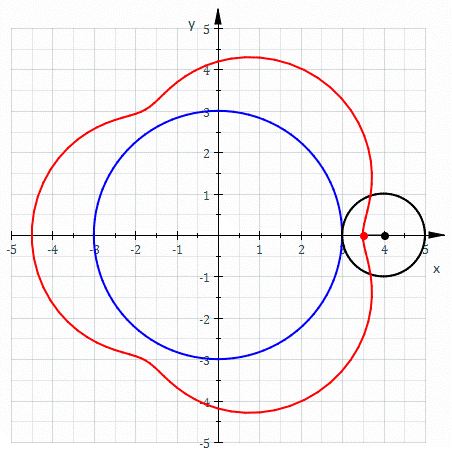
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette. Equations If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R + r) \cos \theta \ - r \cos \left( \frac \theta \right) \\ & y (\theta) = (R + r) \sin \theta \ - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k + 1) \cos \theta - r \cos \left( (k + 1) \theta \right) \\ & y (\theta) = r (k + 1) \sin \theta - r \sin \left( (k + 1) \theta \right) \end in a more concise and complex form :z(\theta) = r \left(e^ - (k + 1)e^ \right) where * angle is in turns: \theta \in , 2\pi * smaller circle has radius * the larger circle has radius Area (Assuming the initial point lies on the larger circle.) When is a pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epicycloid
In geometry, an epicycloid is a plane curve produced by tracing the path of a chosen point on the circumference of a circle—called an ''epicycle''—which rolls without slipping around a fixed circle. It is a particular kind of roulette. Equations If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R + r) \cos \theta \ - r \cos \left( \frac \theta \right) \\ & y (\theta) = (R + r) \sin \theta \ - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k + 1) \cos \theta - r \cos \left( (k + 1) \theta \right) \\ & y (\theta) = r (k + 1) \sin \theta - r \sin \left( (k + 1) \theta \right) \end in a more concise and complex form :z(\theta) = r \left(e^ - (k + 1)e^ \right) where * angle is in turns: \theta \in , 2\pi * smaller circle has radius * the larger circle has radius Area (Assuming the initial point lies on the larger circle.) When is a pos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roulette (curve)
In the differential geometry of curves, a roulette is a kind of curve, generalizing cycloids, epicycloids, hypocycloids, trochoids, epitrochoids, hypotrochoids, and involutes. Definition Informal definition Roughly speaking, a roulette is the curve described by a point (called the ''generator'' or ''pole'') attached to a given curve as that curve rolls without slipping, along a second given curve that is fixed. More precisely, given a curve attached to a plane which is moving so that the curve rolls, without slipping, along a given curve attached to a fixed plane occupying the same space, then a point attached to the moving plane describes a curve, in the fixed plane called a roulette. Special cases and related concepts In the case where the rolling curve is a line and the generator is a point on the line, the roulette is called an involute of the fixed curve. If the rolling curve is a circle and the fixed curve is a line then the roulette is a trochoid. If, in this cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Periodic Functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each function may have many equivalent definitions. Smooth functions All trigonometric functions listed have period 2\pi, unless otherwise stated. For the following trigonometric functions: : is the th up/down number, : is the th Bernoulli number Non-smooth functions The following functions have period p and take x as their argument. The symbol \lfloor n \rfloor is the floor function of n and \sgn is the sign function. Vector-valued functions * Epitrochoid * Epicycloid (special case of the epitrochoid) * Limaçon (special case of the epitrochoid) * Hypotrochoid * Hypocycloid (special case of the hypotrochoid) * Spirograph (special case of the hypotrochoid) Doubly periodic functions * Jacobi's elliptic functions * Weierstrass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limaçon
In geometry, a limaçon or limacon , also known as a limaçon of Pascal or Pascal's Snail, is defined as a roulette curve formed by the path of a point fixed to a circle when that circle rolls around the outside of a circle of equal radius. It can also be defined as the roulette formed when a circle rolls around a circle with half its radius so that the smaller circle is inside the larger circle. Thus, they belong to the family of curves called centered trochoids; more specifically, they are epitrochoids. The cardioid is the special case in which the point generating the roulette lies on the rolling circle; the resulting curve has a cusp. Depending on the position of the point generating the curve, it may have inner and outer loops (giving the family its name), it may be heart-shaped, or it may be oval. A limaçon is a bicircular rational plane algebraic curve of degree 4. History The earliest formal research on limaçons is generally attributed to Étienne Pascal, f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypocycloid
In geometry, a hypocycloid is a special plane curve generated by the trace of a fixed point on a small circle that rolls within a larger circle. As the radius of the larger circle is increased, the hypocycloid becomes more like the cycloid created by rolling a circle on a line. Properties If the smaller circle has radius , and the larger circle has radius , then the parametric equations for the curve can be given by either: :\begin & x (\theta) = (R - r) \cos \theta + r \cos \left(\frac \theta \right) \\ & y (\theta) = (R - r) \sin \theta - r \sin \left( \frac \theta \right) \end or: :\begin & x (\theta) = r (k - 1) \cos \theta + r \cos \left( (k - 1) \theta \right) \\ & y (\theta) = r (k - 1) \sin \theta - r \sin \left( (k - 1) \theta \right) \end If is an integer, then the curve is closed, and has cusps (i.e., sharp corners, where the curve is not differentiable). Specially for the curve is a straight line and the circles are called Cardano circles. Girolamo Cardano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cycloid
In geometry, a cycloid is the curve traced by a point on a circle as it rolls along a straight line without slipping. A cycloid is a specific form of trochoid and is an example of a roulette, a curve generated by a curve rolling on another curve. The cycloid, with the cusps pointing upward, is the curve of fastest descent under uniform gravity (the brachistochrone curve). It is also the form of a curve for which the period of an object in simple harmonic motion (rolling up and down repetitively) along the curve does not depend on the object's starting position (the tautochrone curve). History The cycloid has been called "The Helen of Geometers" as it caused frequent quarrels among 17th-century mathematicians. Historians of mathematics have proposed several candidates for the discoverer of the cycloid. Mathematical historian Paul Tannery cited similar work by the Syrian philosopher Iamblichus as evidence that the curve was known in antiquity. English mathematician ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
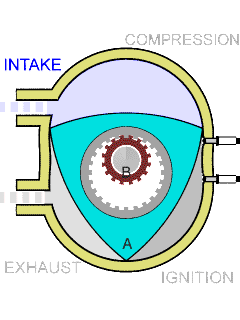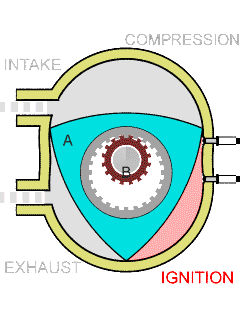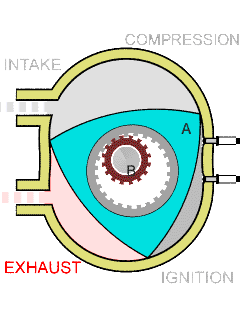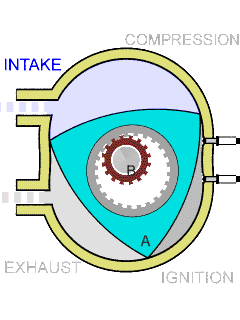
Wankel Engine
The Wankel engine (, ) is a type of internal combustion engine using an eccentric rotary design to convert pressure into rotating motion. It was invented by German engineer Felix Wankel, and designed by German engineer Hanns-Dieter Paschke. The Wankel engine's rotor, which creates the turning motion, is similar in shape to a Reuleaux triangle, with the sides having less curvature. The rotor rotates inside an oval-like epitrochoidal housing, around a central output shaft. The rotor spins in a hula-hoop fashion around the central output shaft, spinning the shaft via toothed gearing. Due to its inherent poor thermodynamics, the Wankel engine has a significantly worse thermal efficiency and worse exhaust gas behaviour when compared against the Otto engine or the Diesel engine, which is why the Wankel engine has seen limited use since its introduction in the 1960s. However, its advantages of compact design, smoothness, lower weight and less parts over the aforementioned reciproca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apsidal Precession
In celestial mechanics, apsidal precession (or apsidal advance) is the precession (gradual rotation) of the line connecting the apsides (line of apsides) of an astronomical body's orbit. The apsides are the orbital points closest (periapsis) and farthest (apoapsis) from its primary body. The apsidal precession is the first time derivative of the argument of periapsis, one of the six main orbital elements of an orbit. Apsidal precession is considered positive when the orbit's axis rotates in the same direction as the orbital motion. An apsidal period is the time interval required for an orbit to precess through 360°. History The ancient Greek astronomer Hipparchus noted the apsidal precession of the Moon's orbit (as the revolution of the Moon's apogee with a period of approximately 8.85 years); it is corrected for in the Antikythera Mechanism (circa 80 BCE) (with the supposed value of 8.88 years per full cycle, correct to within 0.34% of current measurements). The pre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rosetta (orbit)
A Rosetta orbit is a complex type of orbit. In astronomy, a Rosetta orbit occurs when there is a periastron shift during each orbital cycle. A retrograde Newtonian shift can occur when the central mass is extended rather than a point gravitational source, resulting in a non-closed orbit. A prograde relativistic shift happens because of relativistic effects from a massive gravitational source. In barred spiral galaxies with a compact, lens-shaped bar (in contrast with a box-shaped bar), the morphology of the bar is supported by stars following rosette-shaped orbits that rotate with the bar. An object approaching a black hole with an intermediate velocity (not slow enough to spiral into the hole and not fast enough to escape) enters a complex orbit pattern, bounded by a near and far distance to the hole and tracing an oscillating pattern known as a hypotrochoid. In 2020, scientists using observations made by the European Southern Observatory's Very Large Telescope revealed for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hypotrochoid
In geometry, a hypotrochoid is a roulette traced by a point attached to a circle of radius rolling around the inside of a fixed circle of radius , where the point is a distance from the center of the interior circle. The parametric equations for a hypotrochoid are: :\begin & x (\theta) = (R - r)\cos\theta + d\cos\left(\theta\right) \\ & y (\theta) = (R - r)\sin\theta - d\sin\left(\theta\right) \end where is the angle formed by the horizontal and the center of the rolling circle (these are not polar equations because is not the polar angle). When measured in radian, takes values from 0 to 2 \pi \times \tfrac (where is least common multiple). Special cases include the hypocycloid with and the ellipse with and . The eccentricity of the ellipse is :e=\frac becoming 1 when d=r (see Tusi couple). The classic Spirograph toy traces out hypotrochoid and epitrochoid curves. Hypotrochoids describe the support of the eigenvalues of some random matrices with cyclic correlation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |