|
Displacement (vector)
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion. It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. Displacement is the shift in location when an object in motion changes from one position to another. For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity (a vector), whose magnitude is the average speed (a scalar quantity). Formulation A displacement may be formulated as a '' relative position'' (resulting from the motion), that is, as the final position of a point relative to its initial position . The corresponding displacement vector can be defined as the d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician who works in the field of geometry is called a ''List of geometers, geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point (geometry), point, line (geometry), line, plane (geometry), plane, distance, angle, surface (mathematics), surface, and curve, as fundamental concepts. Originally developed to model the physical world, geometry has applications in almost all sciences, and also in art, architecture, and other activities that are related to graphics. Geometry also has applications in areas of mathematics that are apparently unrelated. For example, methods of algebraic geometry are fundamental in Wiles's proof of Fermat's Last Theorem, Wiles's proof of Fermat's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector quantities (in that they have Magnitude (mathematics), magnitude and Direction (geometry), direction). The orientation of an object's acceleration is given by the orientation of the ''net'' force acting on that object. The magnitude of an object's acceleration, as described by Newton's second law, is the combined effect of two causes: * the net balance of all external forces acting onto that object — magnitude is Direct proportionality, directly proportional to this net resulting force; * that object's mass, depending on the materials out of which it is made — magnitude is Inverse proportionality, inversely proportional to the object's mass. The International System of Units, SI unit for acceleration is metre per second squared (, \ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Equipollence (geometry)
In Euclidean geometry, equipollence is a homogeneous relation between directed line segments. Two segments are said to be ''equipollent'' when they have the same length and direction. Two equipollent segments are parallel but not necessarily colinear nor overlapping. For example, a segment ''AB'', from point ''A'' to point ''B'', has the opposite direction to segment ''BA''; thus ''AB'' and ''BA'' are equipollent. Parallelogram property A property of Euclidean spaces is the parallelogram property of vectors: If two segments are equipollent, then they form two sides of a (possibly degenerate) parallelogram: History The concept of equipollent line segments was advanced by Giusto Bellavitis in 1835. Subsequently, the term vector was adopted for a class of equipollent line segments. Bellavitis's use of the idea of a relation to compare different but similar objects has become a common mathematical technique, particularly in the use of equivalence relations. Bellavitis us ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Displacement Field (mechanics)
In mechanics, a displacement field is the assignment of displacement vectors for all points in a region or body that are displaced from one state to another. A displacement vector specifies the position of a point or a particle in reference to an origin or to a previous position. For example, a displacement field may be used to describe the effects of deformation on a solid body. Formulation Before considering displacement, the state before deformation must be defined. It is a state in which the coordinates of all points are known and described by the function: \vec_0: \Omega \to P where *\vec_0 is a placement vector *\Omega are all the points of the body *P are all the points in the space in which the body is present Most often it is a state of the body in which no forces are applied. Then given any other state of this body in which coordinates of all its points are described as \vec_1 the displacement field is the difference between two body states: \vec = \vec_1 - \vec_0 w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Deformation (mechanics)
In physics and continuum mechanics, deformation is the change in the shape (geometry), shape or size of an object. It has dimension (physics), dimension of length with SI unit of metre (m). It is quantified as the residual displacement (geometry), displacement of particles in a non-rigid body, from an configuration to a configuration, excluding the body's average translation (physics), translation and rotation (its rigid transformation). A ''configuration'' is a set containing the position (geometry), positions of all particles of the body. A deformation can occur because of structural load, external loads, intrinsic activity (e.g. muscle contraction), body forces (such as gravity or electromagnetic forces), or changes in temperature, moisture content, or chemical reactions, etc. In a continuous body, a ''deformation field'' results from a Stress (physics), stress field due to applied forces or because of some changes in the conditions of the body. The relation between stre ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Inertial Frame Of Reference
In classical physics and special relativity, an inertial frame of reference (also called an inertial space or a Galilean reference frame) is a frame of reference in which objects exhibit inertia: they remain at rest or in uniform motion relative to the frame until acted upon by external forces. In such a frame, the laws of nature can be observed without the need to correct for acceleration. All frames of reference with zero acceleration are in a state of constant rectilinear motion (straight-line motion) with respect to one another. In such a frame, an object with zero net force acting on it, is perceived to move with a constant velocity, or, equivalently, Newton's laws of motion#Newton's first law, Newton's first law of motion holds. Such frames are known as inertial. Some physicists, like Isaac Newton, originally thought that one of these frames was absolute — the one approximated by the fixed stars. However, this is not required for the definition, and it is now known that t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Absolute Velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector quantity, meaning that both magnitude and direction are needed to define it. The scalar absolute value ( magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the SI (metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Definition Average velocity The average velocity of an object over a period of time is its change in position, \Delta s, divided by the duration of the period, \Delta t, given mathematically as\bar=\frac. Instantaneous velocity The instantaneous velocity of an object is the limit average velocit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
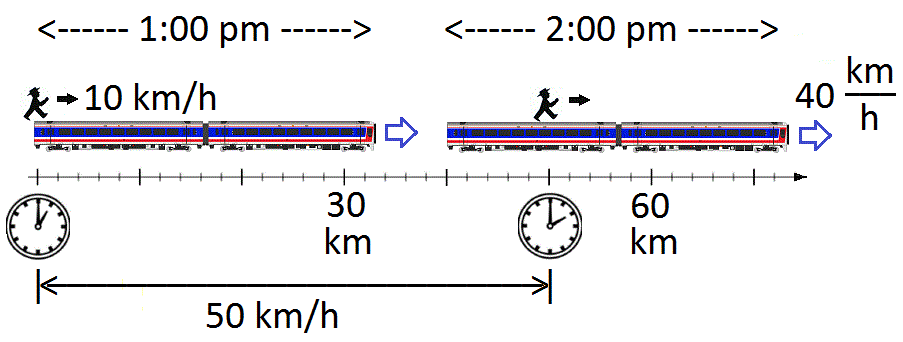
Relative Velocity
The relative velocity of an object ''B'' relative to an observer ''A'', denoted \mathbf v_ (also \mathbf v_ or \mathbf v_), is the velocity vector of ''B'' measured in the rest frame of ''A''. The relative speed v_ = \, \mathbf v_\, is the vector norm of the relative velocity. Classical mechanics In one dimension (non-relativistic) We begin with relative motion in the classical, (or non- relativistic, or the Newtonian approximation) that all speeds are much less than the speed of light. This limit is associated with the Galilean transformation. The figure shows a man on top of a train, at the back edge. At 1:00 pm he begins to walk forward at a walking speed of 10 km/h (kilometers per hour). The train is moving at 40 km/h. The figure depicts the man and train at two different times: first, when the journey began, and also one hour later at 2:00 pm. The figure suggests that the man is 50 km from the starting point after having traveled (by walking and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Time Rate
In mathematics, a rate is the quotient of two quantities, often represented as a fraction. If the divisor (or fraction denominator) in the rate is equal to one expressed as a single unit, and if it is assumed that this quantity can be changed systematically (i.e., is an independent variable), then the dividend (the fraction numerator) of the rate expresses the corresponding rate of change in the other ( dependent) variable. In some cases, it may be regarded as a change to a value, which is caused by a change of a value in respect to another value. For example, acceleration is a change in velocity with respect to time ''Temporal rate'' is a common type of rate ("per unit of time"), such as speed, heart rate, and flux. In fact, often ''rate'' is a synonym of rhythm or frequency, a count per second (i.e., hertz); e.g., radio frequencies or sample rates. In describing the units of a rate, the word "per" is used to separate the units of the two measurements used to calculate the r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Speed
In kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a non-negative scalar quantity. Introduction of the speed/velocity terminology by Prof. Tait, in 1882. The average speed of an object in an interval of time is the distance travelled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as the duration of the time interval approaches zero. Speed is the magnitude of ''velocity'' (a vector), which indicates additionally the direction of motion. Speed has the dimensions of distance divided by time. The SI unit of speed is the metre per second (m/s), but the most common unit of speed in everyday usage is the kilometre per hour (km/h) or, in the US and the UK, miles per hour (mph). For air and marine travel, the knot is commonly used. The fastest possible speed at wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Velocity
Velocity is a measurement of speed in a certain direction of motion. It is a fundamental concept in kinematics, the branch of classical mechanics that describes the motion of physical objects. Velocity is a vector (geometry), vector Physical quantity, quantity, meaning that both magnitude and direction are needed to define it. The Scalar (physics), scalar absolute value (Magnitude (mathematics), magnitude) of velocity is called , being a coherent derived unit whose quantity is measured in the International System of Units, SI (metric system) as metres per second (m/s or m⋅s−1). For example, "5 metres per second" is a scalar, whereas "5 metres per second east" is a vector. If there is a change in speed, direction or both, then the object is said to be undergoing an ''acceleration''. Definition Average velocity The average velocity of an object over a period of time is its Displacement (geometry), change in position, \Delta s, divided by the duration of the period, \Delt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Jounce
In physics, the fourth, fifth and sixth derivatives of position are defined as derivatives of the position vector with respect to time – with the first, second, and third derivatives being velocity, acceleration, and jerk, respectively. The higher-order derivatives are less common than the first three; thus their names are not as standardized, though the concept of a minimum snap trajectory has been used in robotics. The fourth derivative is referred to as snap, leading the fifth and sixth derivatives to be "sometimes somewhat facetiously" called crackle and pop, named after the Rice Krispies mascots of the same name. The fourth derivative is also called jounce. (snap/jounce) Snap, or jounce, is the fourth derivative of the position vector with respect to time, or the rate of change of the jerk with respect to time. Equivalently, it is the second derivative of acceleration or the third derivative of velocity, and is defined by any of the following equivalent expressions: ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |