right eigenvector

In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by $\lambda$, is the factor by which the eigenvector is scaled.

Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated.

Formal definition

If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as
$T(\mathbf) = \lambda \mathbf,$

where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root associated with .

There is a direct correspondence between ''n''-by-''n'' square matrices and linear transformations from an ''n''-dimensional vector space into itself, given any basis of the vector space. Hence, in a finite-dimensional vector space, it is equivalent to define eigenvalues and eigenvectors using either the language of matrices, or the language of linear transformations.

If is finite-dimensional, the above equation is equivalent to
$A\mathbf = \lambda \mathbf.$

where is the matrix representation of and is the coordinate vector of .

Overview

Eigenvalues and eigenvectors feature prominently in the analysis of linear transformations. The prefix '' eigen-'' is adopted from the German word ''eigen'' (cognate with the English word ''own'') for 'proper', 'characteristic', 'own'. Originally used to study principal axes of the rotational motion of rigid bodies, eigenvalues and eigenvectors have a wide range of applications, for example in stability analysis, vibration analysis, atomic orbitals, facial recognition, and matrix diagonalization.

In essence, an eigenvector v of a linear transformation ''T'' is a nonzero vector that, when ''T'' is applied to it, does not change direction. Applying ''T'' to the eigenvector only scales the eigenvector by the scalar value ''λ'', called an eigenvalue. This condition can be written as the equation

$T(\mathbf) = \lambda \mathbf,$

referred to as the eigenvalue equation or eigenequation. In general, ''λ'' may be any scalar. For example, ''λ'' may be negative, in which case the eigenvector reverses direction as part of the scaling, or it may be zero or complex.

The Mona Lisa example pictured here provides a simple illustration. Each point on the painting can be represented as a vector pointing from the center of the painting to that point. The linear transformation in this example is called a shear mapping. Points in the top half are moved to the right, and points in the bottom half are moved to the left, proportional to how far they are from the horizontal axis that goes through the middle of the painting. The vectors pointing to each point in the original image are therefore tilted right or left, and made longer or shorter by the transformation. Points ''along'' the horizontal axis do not move at all when this transformation is applied. Therefore, any vector that points directly to the right or left with no vertical component is an eigenvector of this transformation, because the mapping does not change its direction. Moreover, these eigenvectors all have an eigenvalue equal to one, because the mapping does not change their length either.

Linear transformations can take many different forms, mapping vectors in a variety of vector spaces, so the eigenvectors can also take many forms. For example, the linear transformation could be a differential operator like $\tfrac$, in which case the eigenvectors are functions called eigenfunctions that are scaled by that differential operator, such as

$\frace^ = \lambda e^.$

Alternatively, the linear transformation could take the form of an ''n'' by ''n'' matrix, in which case the eigenvectors are ''n'' by 1 matrices. If the linear transformation is expressed in the form of an ''n'' by ''n'' matrix ''A'', then the eigenvalue equation for a linear transformation above can be rewritten as the matrix multiplication

$A\mathbf v = \lambda \mathbf v,$

where the eigenvector ''v'' is an ''n'' by 1 matrix. For a matrix, eigenvalues and eigenvectors can be used to decompose the matrix—for example by diagonalizing it.

Eigenvalues and eigenvectors give rise to many closely related mathematical concepts, and the prefix ''eigen-'' is applied liberally when naming them:
* The set of all eigenvectors of a linear transformation, each paired with its corresponding eigenvalue, is called the eigensystem of that transformation.
* The set of all eigenvectors of ''T'' corresponding to the same eigenvalue, together with the zero vector, is called an eigenspace, or the characteristic space of ''T'' associated with that eigenvalue.
* If a set of eigenvectors of ''T'' forms a basis of the domain of ''T'', then this basis is called an eigenbasis.

History

Eigenvalues are often introduced in the context of linear algebra or matrix theory. Historically, however, they arose in the study of quadratic forms and differential equations.

In the 18th century, Leonhard Euler studied the rotational motion of a rigid body, and discovered the importance of the principal axes. Joseph-Louis Lagrange saw how their work could be used to classify the quadric surfaces, and generalized it to arbitrary dimensions. Cauchy also coined the term ''racine caractéristique'' (characteristic root), for what is now called ''eigenvalue''; his term survives in '' characteristic equation''.

Later, Joseph Fourier used the work of Lagrange and Pierre-Simon Laplace to solve the heat equation by separation of variables in his famous 1822 book '' Théorie analytique de la chaleur''. Charles-François Sturm developed Fourier's ideas further, and brought them to the attention of Cauchy, who combined them with his own ideas and arrived at the fact that real symmetric matrices have real eigenvalues. This was extended by Charles Hermite in 1855 to what are now called Hermitian matrices.

Around the same time, Francesco Brioschi proved that the eigenvalues of orthogonal matrices lie on the unit circle, and Alfred Clebsch found the corresponding result for skew-symmetric matrices. Finally, Karl Weierstrass clarified an important aspect in the stability theory started by Laplace, by realizing that defective matrices can cause instability.

In the meantime, Joseph Liouville studied eigenvalue problems similar to those of Sturm; the discipline that grew out of their work is now called ''Sturm–Liouville theory''. Schwarz studied the first eigenvalue of Laplace's equation on general domains towards the end of the 19th century, while Poincaré studied Poisson's equation a few years later.

At the start of the 20th century, David Hilbert studied the eigenvalues of integral operators by viewing the operators as infinite matrices. He was the first to use the German word ''eigen'', which means "own", to denote eigenvalues and eigenvectors in 1904, though he may have been following a related usage by Hermann von Helmholtz. For some time, the standard term in English was "proper value", but the more distinctive term "eigenvalue" is the standard today.

The first numerical algorithm for computing eigenvalues and eigenvectors appeared in 1929, when Richard von Mises published the power method. One of the most popular methods today, the QR algorithm, was proposed independently by John G. F. Francis and Vera Kublanovskaya in 1961.

Eigenvalues and eigenvectors of matrices

Eigenvalues and eigenvectors are often introduced to students in the context of linear algebra courses focused on matrices.Cornell University Department of Mathematics (2016
''Lower-Level Courses for Freshmen and Sophomores''
Accessed on 2016-03-27.University of Michigan Mathematics (2016
''Math Course Catalogue''
. Accessed on 2016-03-27.
Furthermore, linear transformations over a finite-dimensional vector space can be represented using matrices, which is especially common in numerical and computational applications.

Consider -dimensional vectors that are formed as a list of scalars, such as the three-dimensional vectors
$\mathbf x = \begin1\\-3\\4\end\quad\mbox\quad \mathbf y = \begin-20\\60\\-80\end.$

These vectors are said to be scalar multiples of each other, or parallel or collinear, if there is a scalar such that
$\mathbf x = \lambda \mathbf y.$

In this case $\lambda = -\frac$.

Now consider the linear transformation of -dimensional vectors defined by an by matrix ,
$A \mathbf v = \mathbf w,$

or
$\begin A_ & A_ & \cdots & A_ \\ A_ & A_ & \cdots & A_ \\ \vdots & \vdots & \ddots & \vdots \\ A_ & A_ & \cdots & A_ \\ \end\begin v_1 \\ v_2 \\ \vdots \\ v_n \end = \begin w_1 \\ w_2 \\ \vdots \\ w_n \end$

where, for each row,
$w_i = A_ v_1 + A_ v_2 + \cdots + A_ v_n = \sum_^n A_ v_j.$

If it occurs that and are scalar multiples, that is if

then is an eigenvector of the linear transformation and the scale factor is the eigenvalue corresponding to that eigenvector. Equation () is the eigenvalue equation for the matrix .

Equation () can be stated equivalently as

where is the by identity matrix and 0 is the zero vector.

Eigenvalues and the characteristic polynomial

Equation () has a nonzero solution ''v'' if and only if the determinant of the matrix is zero. Therefore, the eigenvalues of ''A'' are values of ''λ'' that satisfy the equation

Using the Leibniz formula for determinants, the left-hand side of Equation () is a polynomial function of the variable ''λ'' and the degree of this polynomial is ''n'', the order of the matrix ''A''. Its coefficients depend on the entries of ''A'', except that its term of degree ''n'' is always (−1)^''n''''λ''^''n''. This polynomial is called the ''characteristic polynomial'' of ''A''. Equation () is called the ''characteristic equation'' or the ''secular equation'' of ''A''.

The fundamental theorem of algebra implies that the characteristic polynomial of an ''n''-by-''n'' matrix ''A'', being a polynomial of degree ''n'', can be factored into the product of ''n'' linear terms,

where each ''λ''_''i'' may be real but in general is a complex number. The numbers ''λ''₁, ''λ''₂, ..., ''λ''_''n'', which may not all have distinct values, are roots of the polynomial and are the eigenvalues of ''A''.

As a brief example, which is described in more detail in the examples section later, consider the matrix
$A = \begin 2 & 1\\ 1 & 2 \end.$

Taking the determinant of , the characteristic polynomial of ''A'' is
$, A - \lambda I, = \begin 2 - \lambda & 1 \\ 1 & 2 - \lambda \end = 3 - 4\lambda + \lambda^2.$

Setting the characteristic polynomial equal to zero, it has roots at and , which are the two eigenvalues of ''A''. The eigenvectors corresponding to each eigenvalue can be found by solving for the components of v in the equation In this example, the eigenvectors are any nonzero scalar multiples of
$\mathbf v_ = \begin 1 \\ -1 \end, \quad \mathbf v_ = \begin 1 \\ 1 \end.$

If the entries of the matrix ''A'' are all real numbers, then the coefficients of the characteristic polynomial will also be real numbers, but the eigenvalues may still have nonzero imaginary parts. The entries of the corresponding eigenvectors therefore may also have nonzero imaginary parts. Similarly, the eigenvalues may be irrational numbers even if all the entries of ''A'' are rational numbers or even if they are all integers. However, if the entries of ''A'' are all algebraic numbers, which include the rationals, the eigenvalues are complex algebraic numbers.

The non-real roots of a real polynomial with real coefficients can be grouped into pairs of complex conjugates, namely with the two members of each pair having imaginary parts that differ only in sign and the same real part. If the degree is odd, then by the intermediate value theorem at least one of the roots is real. Therefore, any real matrix with odd order has at least one real eigenvalue, whereas a real matrix with even order may not have any real eigenvalues. The eigenvectors associated with these complex eigenvalues are also complex and also appear in complex conjugate pairs.

Algebraic multiplicity

Let ''λ''_''i'' be an eigenvalue of an ''n'' by ''n'' matrix ''A''. The algebraic multiplicity ''μ''_''A''(''λ''_''i'') of the eigenvalue is its multiplicity as a root of the characteristic polynomial, that is, the largest integer ''k'' such that (''λ'' − ''λ''_''i'')^''k'' divides evenly that polynomial.

Suppose a matrix ''A'' has dimension ''n'' and ''d'' ≤ ''n'' distinct eigenvalues. Whereas Equation () factors the characteristic polynomial of ''A'' into the product of ''n'' linear terms with some terms potentially repeating, the characteristic polynomial can instead be written as the product of ''d'' terms each corresponding to a distinct eigenvalue and raised to the power of the algebraic multiplicity,
$, A - \lambda I, = (\lambda_1 - \lambda)^(\lambda_2 - \lambda)^ \cdots (\lambda_d - \lambda)^.$

If ''d'' = ''n'' then the right-hand side is the product of ''n'' linear terms and this is the same as Equation (). The size of each eigenvalue's algebraic multiplicity is related to the dimension ''n'' as
$\begin 1 &\leq \mu_A(\lambda_i) \leq n, \\ \mu_A &= \sum_^d \mu_A\left(\lambda_i\right) = n. \end$

If ''μ''_''A''(''λ''_''i'') = 1, then ''λ''_''i'' is said to be a ''simple eigenvalue''. If ''μ''_''A''(''λ''_''i'') equals the geometric multiplicity of ''λ''_''i'', ''γ''_''A''(''λ''_''i''), defined in the next section, then ''λ''_''i'' is said to be a ''semisimple eigenvalue''.

Eigenspaces, geometric multiplicity, and the eigenbasis for matrices

Given a particular eigenvalue ''λ'' of the ''n'' by ''n'' matrix ''A'', define the set ''E'' to be all vectors v that satisfy Equation (),
$E = \left\.$

On one hand, this set is precisely the kernel or nullspace of the matrix (''A'' − ''λI''). On the other hand, by definition, any nonzero vector that satisfies this condition is an eigenvector of ''A'' associated with ''λ''. So, the set ''E'' is the Union (set theory), union of the zero vector with the set of all eigenvectors of ''A'' associated with ''λ'', and ''E'' equals the nullspace of (''A'' − ''λI''). ''E'' is called the eigenspace or characteristic space of ''A'' associated with ''λ''. In general ''λ'' is a complex number and the eigenvectors are complex ''n'' by 1 matrices. A property of the nullspace is that it is a linear subspace, so ''E'' is a linear subspace of $\mathbb^n$.

Because the eigenspace ''E'' is a linear subspace, it is closure (mathematics), closed under addition. That is, if two vectors u and v belong to the set ''E'', written , then or equivalently . This can be checked using the distributive property of matrix multiplication. Similarly, because ''E'' is a linear subspace, it is closed under scalar multiplication. That is, if and ''α'' is a complex number, or equivalently . This can be checked by noting that multiplication of complex matrices by complex numbers is commutative property, commutative. As long as u + v and ''α''v are not zero, they are also eigenvectors of ''A'' associated with ''λ''.

The dimension of the eigenspace ''E'' associated with ''λ'', or equivalently the maximum number of linearly independent eigenvectors associated with ''λ'', is referred to as the eigenvalue's geometric multiplicity ''γ''_''A''(''λ''). Because ''E'' is also the nullspace of (''A'' − ''λI''), the geometric multiplicity of ''λ'' is the dimension of the nullspace of (''A'' − ''λI''), also called the ''nullity'' of (''A'' − ''λI''), which relates to the dimension and rank of (''A'' − ''λI'') as
$\gamma_A(\lambda) = n - \operatorname(A - \lambda I).$

Because of the definition of eigenvalues and eigenvectors, an eigenvalue's geometric multiplicity must be at least one, that is, each eigenvalue has at least one associated eigenvector. Furthermore, an eigenvalue's geometric multiplicity cannot exceed its algebraic multiplicity. Additionally, recall that an eigenvalue's algebraic multiplicity cannot exceed ''n''.
$1 \le \gamma_A(\lambda) \le \mu_A(\lambda) \le n$

To prove the inequality $\gamma_A(\lambda)\le\mu_A(\lambda)$, consider how the definition of geometric multiplicity implies the existence of $\gamma_A(\lambda)$ Orthonormality, orthonormal eigenvectors $\boldsymbol_1,\, \ldots,\, \boldsymbol_$, such that $A \boldsymbol_k = \lambda \boldsymbol_k$. We can therefore find a (unitary) matrix $V$ whose first $\gamma_A(\lambda)$ columns are these eigenvectors, and whose remaining columns can be any orthonormal set of $n - \gamma_A(\lambda)$ vectors orthogonal to these eigenvectors of $A$. Then $V$ has full rank and is therefore invertible, and $AV=VD$ with $D$ a matrix whose top left block is the diagonal matrix $\lambda I_$. This implies that $(A - \xi I)V = V(D - \xi I)$. In other words, $A - \xi I$ is similar to $D - \xi I$, which implies that $\det(A - \xi I) = \det(D - \xi I)$. But from the definition of $D$ we know that $\det(D - \xi I)$ contains a factor $(\xi - \lambda)^$, which means that the algebraic multiplicity of $\lambda$ must satisfy $\mu_A(\lambda) \ge \gamma_A(\lambda)$.

Suppose $A$ has $d \leq n$ distinct eigenvalues $\lambda_1, \ldots, \lambda_d$, where the geometric multiplicity of $\lambda_i$ is $\gamma_A (\lambda_i)$. The total geometric multiplicity of $A$,
$\begin \gamma_A &= \sum_^d \gamma_A(\lambda_i), \\ d &\le \gamma_A \le n, \end$

is the dimension of the Linear subspace#Sum, sum of all the eigenspaces of $A$'s eigenvalues, or equivalently the maximum number of linearly independent eigenvectors of $A$. If $\gamma_A=n$, then
* The direct sum of the eigenspaces of all of $A$'s eigenvalues is the entire vector space $\mathbb^n$.
* A basis of $\mathbb^n$ can be formed from $n$ linearly independent eigenvectors of $A$; such a basis is called an eigenbasis
* Any vector in $\mathbb^n$ can be written as a linear combination of eigenvectors of $A$.

Additional properties of eigenvalues

Let $A$ be an arbitrary $n \times n$ matrix of complex numbers with eigenvalues $\lambda_1, \ldots, \lambda_n$. Each eigenvalue appears $\mu_A(\lambda_i)$ times in this list, where $\mu_A(\lambda_i)$ is the eigenvalue's algebraic multiplicity. The following are properties of this matrix and its eigenvalues:
* The trace (linear algebra), trace of $A$, defined as the sum of its diagonal elements, is also the sum of all eigenvalues,
*: $\operatorname(A) = \sum_^n a_ = \sum_^n \lambda_i = \lambda_1 + \lambda_2 + \cdots + \lambda_n.$
* The determinant of $A$ is the product of all its eigenvalues,
*: $\det(A) = \prod_^n \lambda_i = \lambda_1\lambda_2 \cdots \lambda_n.$
* The eigenvalues of the $k$^th power of $A$; i.e., the eigenvalues of $A^k$, for any positive integer $k$, are $\lambda_1^k, \ldots, \lambda_n^k$.
* The matrix $A$ is invertible matrix, invertible if and only if every eigenvalue is nonzero.
* If $A$ is invertible, then the eigenvalues of $A^$ are $\frac, \ldots, \frac$ and each eigenvalue's geometric multiplicity coincides. Moreover, since the characteristic polynomial of the inverse is the reciprocal polynomial of the original, the eigenvalues share the same algebraic multiplicity.
* If $A$ is equal to its conjugate transpose $A^*$, or equivalently if $A$ is Hermitian matrix, Hermitian, then every eigenvalue is real. The same is true of any symmetric matrix, symmetric real matrix.
* If $A$ is not only Hermitian but also positive-definite matrix, positive-definite, positive-semidefinite, negative-definite, or negative-semidefinite, then every eigenvalue is positive, non-negative, negative, or non-positive, respectively.
* If $A$ is unitary matrix, unitary, every eigenvalue has absolute value $, \lambda_i, =1$.
* if $A$ is a $n\times n$ matrix and $\$ are its eigenvalues, then the eigenvalues of matrix $I+A$ (where $I$ is the identity matrix) are $\$. Moreover, if $\alpha\in\mathbb C$, the eigenvalues of $\alpha I+A$ are $\$. More generally, for a polynomial $P$ the eigenvalues of matrix $P(A)$ are $\$.

Left and right eigenvectors

Many disciplines traditionally represent vectors as matrices with a single column rather than as matrices with a single row. For that reason, the word "eigenvector" in the context of matrices almost always refers to a right eigenvector, namely a ''column'' vector that ''right'' multiplies the $n \times n$ matrix $A$ in the defining equation, Equation (),
$A \mathbf v = \lambda \mathbf v.$

The eigenvalue and eigenvector problem can also be defined for ''row'' vectors that ''left'' multiply matrix $A$. In this formulation, the defining equation is
$\mathbf u A = \kappa \mathbf u,$

where $\kappa$ is a scalar and $u$ is a $1 \times n$ matrix. Any row vector $u$ satisfying this equation is called a left eigenvector of $A$ and $\kappa$ is its associated eigenvalue. Taking the transpose of this equation,
$A^\textsf \mathbf u^\textsf = \kappa \mathbf u^\textsf.$

Comparing this equation to Equation (), it follows immediately that a left eigenvector of $A$ is the same as the transpose of a right eigenvector of $A^\textsf$, with the same eigenvalue. Furthermore, since the characteristic polynomial of $A^\textsf$ is the same as the characteristic polynomial of $A$, the eigenvalues of the left eigenvectors of $A$ are the same as the eigenvalues of the right eigenvectors of $A^\textsf$.

Diagonalization and the eigendecomposition

Suppose the eigenvectors of ''A'' form a basis, or equivalently ''A'' has ''n'' linearly independent eigenvectors v₁, v₂, ..., v_''n'' with associated eigenvalues ''λ''₁, ''λ''₂, ..., ''λ''_''n''. The eigenvalues need not be distinct. Define a square matrix ''Q'' whose columns are the ''n'' linearly independent eigenvectors of ''A'',
: $Q = \begin \mathbf v_1 & \mathbf v_2 & \cdots & \mathbf v_n \end.$

Since each column of ''Q'' is an eigenvector of ''A'', right multiplying ''A'' by ''Q'' scales each column of ''Q'' by its associated eigenvalue,
: $AQ = \begin \lambda_1 \mathbf v_1 & \lambda_2 \mathbf v_2 & \cdots & \lambda_n \mathbf v_n \end.$

With this in mind, define a diagonal matrix Λ where each diagonal element Λ_''ii'' is the eigenvalue associated with the ''i''th column of ''Q''. Then
: $AQ = Q\Lambda.$

Because the columns of ''Q'' are linearly independent, Q is invertible. Right multiplying both sides of the equation by ''Q''⁻¹,
: $A = Q\Lambda Q^,$

or by instead left multiplying both sides by ''Q''⁻¹,
: $Q^AQ = \Lambda.$

''A'' can therefore be decomposed into a matrix composed of its eigenvectors, a diagonal matrix with its eigenvalues along the diagonal, and the inverse of the matrix of eigenvectors. This is called the eigendecomposition of a matrix, eigendecomposition and it is a matrix similarity, similarity transformation. Such a matrix ''A'' is said to be ''similar'' to the diagonal matrix Λ or ''diagonalizable matrix, diagonalizable''. The matrix ''Q'' is the change of basis matrix of the similarity transformation. Essentially, the matrices ''A'' and Λ represent the same linear transformation expressed in two different bases. The eigenvectors are used as the basis when representing the linear transformation as Λ.

Conversely, suppose a matrix ''A'' is diagonalizable. Let ''P'' be a non-singular square matrix such that ''P''⁻¹''AP'' is some diagonal matrix ''D''. Left multiplying both by ''P'', . Each column of ''P'' must therefore be an eigenvector of ''A'' whose eigenvalue is the corresponding diagonal element of ''D''. Since the columns of ''P'' must be linearly independent for ''P'' to be invertible, there exist ''n'' linearly independent eigenvectors of ''A''. It then follows that the eigenvectors of ''A'' form a basis if and only if ''A'' is diagonalizable.

A matrix that is not diagonalizable is said to be defective matrix, defective. For defective matrices, the notion of eigenvectors generalizes to generalized eigenvectors and the diagonal matrix of eigenvalues generalizes to the Jordan normal form. Over an algebraically closed field, any matrix ''A'' has a Jordan normal form and therefore admits a basis of generalized eigenvectors and a decomposition into generalized eigenspaces.

Variational characterization

In the Hermitian matrix, Hermitian case, eigenvalues can be given a variational characterization. The largest eigenvalue of $H$ is the maximum value of the quadratic form $\mathbf x^\textsf H \mathbf x / \mathbf x^\textsf \mathbf x$. A value of $\mathbf x$ that realizes that maximum, is an eigenvector.

Matrix examples

Two-dimensional matrix example

Consider the matrix
$A = \begin 2 & 1\\ 1 & 2 \end.$

The figure on the right shows the effect of this transformation on point coordinates in the plane. The eigenvectors ''v'' of this transformation satisfy Equation (), and the values of ''λ'' for which the determinant of the matrix (''A'' − ''λI'') equals zero are the eigenvalues.

Taking the determinant to find characteristic polynomial of ''A'',
$\begin , A - \lambda I, &= \left, \begin 2 & 1 \\ 1 & 2 \end - \lambda\begin 1 & 0 \\ 0 & 1 \end\ = \begin 2 - \lambda & 1 \\ 1 & 2 - \lambda \end \\[6pt] &= 3 - 4\lambda + \lambda^2 \\[6pt] &= (\lambda - 3)(\lambda - 1). \end$

Setting the characteristic polynomial equal to zero, it has roots at and , which are the two eigenvalues of ''A''.

For , Equation () becomes,
$(A - I)\mathbf_ = \begin 1 & 1\\ 1 & 1\end\beginv_1 \\ v_2\end = \begin0 \\ 0\end$
$1v_1 + 1v_2 = 0$

Any nonzero vector with ''v''₁ = −''v''₂ solves this equation. Therefore,
$\mathbf_ = \begin v_1 \\ -v_1 \end = \begin 1 \\ -1 \end$
is an eigenvector of ''A'' corresponding to ''λ'' = 1, as is any scalar multiple of this vector.

For , Equation () becomes
$\begin (A - 3I)\mathbf_ &= \begin -1 & 1\\ 1 & -1 \end \begin v_1 \\ v_2 \end = \begin 0 \\ 0 \end \\ -1v_1 + 1v_2 &= 0;\\ 1v_1 - 1v_2 &= 0 \end$

Any nonzero vector with ''v''₁ = ''v''₂ solves this equation. Therefore,
$\mathbf v_ = \begin v_1 \\ v_1 \end = \begin 1 \\ 1 \end$

is an eigenvector of ''A'' corresponding to ''λ'' = 3, as is any scalar multiple of this vector.

Thus, the vectors v_''λ''=1 and v_''λ''=3 are eigenvectors of ''A'' associated with the eigenvalues and , respectively.

Three-dimensional matrix example

Consider the matrix
$A = \begin 2 & 0 & 0 \\ 0 & 3 & 4 \\ 0 & 4 & 9 \end.$

The characteristic polynomial of ''A'' is
$\begin , A-\lambda I, &= \left, \begin 2 & 0 & 0 \\ 0 & 3 & 4 \\ 0 & 4 & 9 \end - \lambda\begin 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end\ = \begin 2 - \lambda & 0 & 0 \\ 0 & 3 - \lambda & 4 \\ 0 & 4 & 9 - \lambda \end, \\[6pt] &= (2 - \lambda)\bigl[(3 - \lambda)(9 - \lambda) - 16\bigr] = -\lambda^3 + 14\lambda^2 - 35\lambda + 22. \end$

The roots of the characteristic polynomial are 2, 1, and 11, which are the only three eigenvalues of ''A''. These eigenvalues correspond to the eigenvectors and or any nonzero multiple thereof.

Three-dimensional matrix example with complex eigenvalues

Consider the permutation matrix, cyclic permutation matrix
$A = \begin 0 & 1 & 0\\ 0 & 0 & 1\\ 1 & 0 & 0 \end.$

This matrix shifts the coordinates of the vector up by one position and moves the first coordinate to the bottom. Its characteristic polynomial is 1 − ''λ''³, whose roots are
$\begin \lambda_1 &= 1 \\ \lambda_2 &= -\frac + i \frac \\ \lambda_3 &= \lambda_2^* = -\frac - i \frac \end$

where $i$ is an imaginary unit with

For the real eigenvalue ''λ''₁ = 1, any vector with three equal nonzero entries is an eigenvector. For example,
$A \begin 5\\ 5\\ 5 \end = \begin 5\\ 5\\ 5 \end = 1 \cdot \begin 5\\ 5\\ 5 \end.$

For the complex conjugate pair of imaginary eigenvalues,
$\lambda_2\lambda_3 = 1, \quad \lambda_2^2 = \lambda_3, \quad \lambda_3^2 = \lambda_2.$

Then
$A \begin 1 \\ \lambda_2 \\ \lambda_3 \end = \begin \lambda_2 \\ \lambda_3 \\ 1 \end = \lambda_2 \cdot \begin 1 \\ \lambda_2 \\ \lambda_3 \end,$

and
$A \begin 1 \\ \lambda_3 \\ \lambda_2 \end = \begin \lambda_3 \\ \lambda_2 \\ 1 \end = \lambda_3 \cdot \begin 1 \\ \lambda_3 \\ \lambda_2 \end.$

Therefore, the other two eigenvectors of ''A'' are complex and are $\mathbf v_ = \begin 1 & \lambda_2 & \lambda_3\end^\textsf$ and $\mathbf v_ = \begin 1 & \lambda_3 & \lambda_2\end^\textsf$ with eigenvalues ''λ''₂ and ''λ''₃, respectively. The two complex eigenvectors also appear in a complex conjugate pair,
$\mathbf v_ = \mathbf v_^*.$

Diagonal matrix example

Matrices with entries only along the main diagonal are called ''diagonal matrices''. The eigenvalues of a diagonal matrix are the diagonal elements themselves. Consider the matrix
$A = \begin 1 & 0 & 0\\ 0 & 2 & 0\\ 0 & 0 & 3\end.$

The characteristic polynomial of ''A'' is
$, A - \lambda I, = (1 - \lambda)(2 - \lambda)(3 - \lambda),$

which has the roots , , and . These roots are the diagonal elements as well as the eigenvalues of ''A''.

Each diagonal element corresponds to an eigenvector whose only nonzero component is in the same row as that diagonal element. In the example, the eigenvalues correspond to the eigenvectors,
$\mathbf v_ = \begin 1\\ 0\\ 0 \end,\quad \mathbf v_ = \begin 0\\ 1\\ 0 \end,\quad \mathbf v_ = \begin 0\\ 0\\ 1 \end,$

respectively, as well as scalar multiples of these vectors.

Triangular matrix example

A matrix whose elements above the main diagonal are all zero is called a ''lower triangular matrix'', while a matrix whose elements below the main diagonal are all zero is called an ''upper triangular matrix''. As with diagonal matrices, the eigenvalues of triangular matrices are the elements of the main diagonal.

Consider the lower triangular matrix,
$A = \begin 1 & 0 & 0\\ 1 & 2 & 0\\ 2 & 3 & 3 \end.$

The characteristic polynomial of ''A'' is
$, A - \lambda I, = (1 - \lambda)(2 - \lambda)(3 - \lambda),$

which has the roots , , and . These roots are the diagonal elements as well as the eigenvalues of ''A''.

These eigenvalues correspond to the eigenvectors,
$\mathbf v_ = \begin 1\\ -1\\ \frac\end,\quad \mathbf v_ = \begin 0\\ 1\\ -3\end,\quad \mathbf v_ = \begin 0\\ 0\\ 1\end,$

respectively, as well as scalar multiples of these vectors.

Matrix with repeated eigenvalues example

As in the previous example, the lower triangular matrix
$A = \begin 2 & 0 & 0 & 0 \\ 1 & 2 & 0 & 0 \\ 0 & 1 & 3 & 0 \\ 0 & 0 & 1 & 3 \end,$

has a characteristic polynomial that is the product of its diagonal elements,
$, A - \lambda I, = \begin 2 - \lambda & 0 & 0 & 0 \\ 1 & 2- \lambda & 0 & 0 \\ 0 & 1 & 3- \lambda & 0 \\ 0 & 0 & 1 & 3- \lambda \end = (2 - \lambda)^2(3 - \lambda)^2.$

The roots of this polynomial, and hence the eigenvalues, are 2 and 3. The ''algebraic multiplicity'' of each eigenvalue is 2; in other words they are both double roots. The sum of the algebraic multiplicities of all distinct eigenvalues is ''μ''_''A'' = 4 = ''n'', the order of the characteristic polynomial and the dimension of ''A''.

On the other hand, the ''geometric multiplicity'' of the eigenvalue 2 is only 1, because its eigenspace is spanned by just one vector $\begin 0 & 1 & -1 & 1 \end^\textsf$ and is therefore 1-dimensional. Similarly, the geometric multiplicity of the eigenvalue 3 is 1 because its eigenspace is spanned by just one vector $\begin 0 & 0 & 0 & 1 \end^\textsf$. The total geometric multiplicity ''γ''_''A'' is 2, which is the smallest it could be for a matrix with two distinct eigenvalues. Geometric multiplicities are defined in a later section.

Eigenvector-eigenvalue identity

For a Hermitian matrix, the norm squared of the ''j''th component of a normalized eigenvector can be calculated using only the matrix eigenvalues and the eigenvalues of the corresponding Minor (linear algebra), minor matrix,
$, v_, ^2 = \frac,$
where $M_j$ is the submatrix formed by removing the ''j''th row and column from the original matrix. This identity also extends to Diagonalizable matrix, diagonalizable matrices, and has been rediscovered many times in the literature.

Eigenvalues and eigenfunctions of differential operators

The definitions of eigenvalue and eigenvectors of a linear transformation ''T'' remains valid even if the underlying vector space is an infinite-dimensional Hilbert space, Hilbert or Banach space. A widely used class of linear transformations acting on infinite-dimensional spaces are the differential operators on function spaces. Let ''D'' be a linear differential operator on the space C^∞ of infinitely derivative, differentiable real functions of a real argument ''t''. The eigenvalue equation for ''D'' is the differential equation
$D f(t) = \lambda f(t)$

The functions that satisfy this equation are eigenvectors of ''D'' and are commonly called eigenfunctions.

Derivative operator example

Consider the derivative operator $\tfrac$ with eigenvalue equation
$\fracf(t) = \lambda f(t).$

This differential equation can be solved by multiplying both sides by ''dt''/''f''(''t'') and integrating. Its solution, the exponential function
$f(t) = f(0)e^,$

is the eigenfunction of the derivative operator. In this case the eigenfunction is itself a function of its associated eigenvalue. In particular, for ''λ'' = 0 the eigenfunction ''f''(''t'') is a constant.

The main eigenfunction article gives other examples.

General definition

The concept of eigenvalues and eigenvectors extends naturally to arbitrary linear map, linear transformations on arbitrary vector spaces. Let ''V'' be any vector space over some field (algebra), field ''K'' of scalar (mathematics), scalars, and let ''T'' be a linear transformation mapping ''V'' into ''V'',
$T:V \to V.$

We say that a nonzero vector v ∈ ''V'' is an eigenvector of ''T'' if and only if there exists a scalar ''λ'' ∈ ''K'' such that

This equation is called the eigenvalue equation for ''T'', and the scalar ''λ'' is the eigenvalue of ''T'' corresponding to the eigenvector v. ''T''(v) is the result of applying the transformation ''T'' to the vector v, while ''λ''v is the product of the scalar ''λ'' with v.

Eigenspaces, geometric multiplicity, and the eigenbasis

Given an eigenvalue ''λ'', consider the set
$E = \left\,$

which is the union of the zero vector with the set of all eigenvectors associated with ''λ''. ''E'' is called the eigenspace or characteristic space of ''T'' associated with ''λ''.

By definition of a linear transformation,
$\begin T(\mathbf + \mathbf) &= T(\mathbf) + T(\mathbf),\\ T(\alpha \mathbf) &= \alpha T(\mathbf), \end$

for x, y ∈ ''V'' and ''α'' ∈ ''K''. Therefore, if u and v are eigenvectors of ''T'' associated with eigenvalue ''λ'', namely u, v ∈ ''E'', then
$\begin T(\mathbf + \mathbf) &= \lambda (\mathbf + \mathbf),\\ T(\alpha \mathbf) &= \lambda (\alpha \mathbf). \end$

So, both u + v and αv are either zero or eigenvectors of ''T'' associated with ''λ'', namely u + v, ''α''v ∈ ''E'', and ''E'' is closed under addition and scalar multiplication. The eigenspace ''E'' associated with ''λ'' is therefore a linear subspace of ''V''.
If that subspace has dimension 1, it is sometimes called an eigenline.

The geometric multiplicity ''γ''_''T''(''λ'') of an eigenvalue ''λ'' is the dimension of the eigenspace associated with ''λ'', i.e., the maximum number of linearly independent eigenvectors associated with that eigenvalue. By the definition of eigenvalues and eigenvectors, ''γ''_''T''(''λ'') ≥ 1 because every eigenvalue has at least one eigenvector.

The eigenspaces of ''T'' always form a direct sum. As a consequence, eigenvectors of ''different'' eigenvalues are always linearly independent. Therefore, the sum of the dimensions of the eigenspaces cannot exceed the dimension ''n'' of the vector space on which ''T'' operates, and there cannot be more than ''n'' distinct eigenvalues.

Any subspace spanned by eigenvectors of ''T'' is an invariant subspace of ''T'', and the restriction of ''T'' to such a subspace is diagonalizable. Moreover, if the entire vector space ''V'' can be spanned by the eigenvectors of ''T'', or equivalently if the direct sum of the eigenspaces associated with all the eigenvalues of ''T'' is the entire vector space ''V'', then a basis of ''V'' called an eigenbasis can be formed from linearly independent eigenvectors of ''T''. When ''T'' admits an eigenbasis, ''T'' is diagonalizable.

Spectral theory

If ''λ'' is an eigenvalue of ''T'', then the operator (''T'' − ''λI'') is not one-to-one, and therefore its inverse (''T'' − ''λI'')⁻¹ does not exist. The converse is true for finite-dimensional vector spaces, but not for infinite-dimensional vector spaces. In general, the operator (''T'' − ''λI'') may not have an inverse even if ''λ'' is not an eigenvalue.

For this reason, in functional analysis eigenvalues can be generalized to the spectrum (functional analysis), spectrum of a linear operator ''T'' as the set of all scalars ''λ'' for which the operator (''T'' − ''λI'') has no bounded operator, bounded inverse. The spectrum of an operator always contains all its eigenvalues but is not limited to them.

Associative algebras and representation theory

One can generalize the algebraic object that is acting on the vector space, replacing a single operator acting on a vector space with an algebra representation – an associative algebra acting on a module (mathematics), module. The study of such actions is the field of representation theory.

The weight (representation theory), representation-theoretical concept of weight is an analog of eigenvalues, while ''weight vectors'' and ''weight spaces'' are the analogs of eigenvectors and eigenspaces, respectively.

Dynamic equations

The simplest difference equations have the form
: $x_t = a_1 x_ + a_2 x_ + \cdots + a_k x_.$

The solution of this equation for ''x'' in terms of ''t'' is found by using its characteristic equation
: $\lambda^k - a_1\lambda^ - a_2\lambda^ - \cdots - a_\lambda-a_k = 0,$

which can be found by stacking into matrix form a set of equations consisting of the above difference equation and the ''k'' – 1 equations $x_ = x_,\ \dots,\ x_ = x_,$ giving a ''k''-dimensional system of the first order in the stacked variable vector $\begin x_t & \cdots & x_ \end$ in terms of its once-lagged value, and taking the characteristic equation of this system's matrix. This equation gives ''k'' characteristic roots $\lambda_1,\, \ldots,\, \lambda_k,$ for use in the solution equation
: $x_t = c_1\lambda_1^t + \cdots + c_k\lambda_k^t.$

A similar procedure is used for solving a differential equation of the form
: $\frac + a_\frac + \cdots + a_1\frac + a_0 x = 0.$

Calculation

The calculation of eigenvalues and eigenvectors is a topic where theory, as presented in elementary linear algebra textbooks, is often very far from practice.

Classical method

The classical method is to first find the eigenvalues, and then calculate the eigenvectors for each eigenvalue. It is in several ways poorly suited for non-exact arithmetics such as floating-point.

Eigenvalues

The eigenvalues of a matrix $A$ can be determined by finding the roots of the characteristic polynomial. This is easy for $2 \times 2$ matrices, but the difficulty increases rapidly with the size of the matrix.

In theory, the coefficients of the characteristic polynomial can be computed exactly, since they are sums of products of matrix elements; and there are algorithms that can find all the roots of a polynomial of arbitrary degree to any required accuracy. However, this approach is not viable in practice because the coefficients would be contaminated by unavoidable round-off errors, and the roots of a polynomial can be an extremely sensitive function of the coefficients (as exemplified by Wilkinson's polynomial). Even for matrices whose elements are integers the calculation becomes nontrivial, because the sums are very long; the constant term is the determinant, which for an $n \times n$ matrix is a sum of $n!$ different products.

Explicit algebraic solution, algebraic formulas for the roots of a polynomial exist only if the degree $n$ is 4 or less. According to the Abel–Ruffini theorem there is no general, explicit and exact algebraic formula for the roots of a polynomial with degree 5 or more. (Generality matters because any polynomial with degree $n$ is the characteristic polynomial of some companion matrix of order $n$.) Therefore, for matrices of order 5 or more, the eigenvalues and eigenvectors cannot be obtained by an explicit algebraic formula, and must therefore be computed by approximate numerical methods. Even the Cubic function#General solution to the cubic equation with real coefficients, exact formula for the roots of a degree 3 polynomial is numerically impractical.

Eigenvectors

Once the (exact) value of an eigenvalue is known, the corresponding eigenvectors can be found by finding nonzero solutions of the eigenvalue equation, that becomes a linear system, system of linear equations with known coefficients. For example, once it is known that 6 is an eigenvalue of the matrix
$A = \begin 4 & 1\\ 6 & 3\end$

we can find its eigenvectors by solving the equation $A v = 6 v$, that is
$\begin 4 & 1\\ 6 & 3\end\beginx \\y\end = 6 \cdot \beginx \\y\end$

This matrix equation is equivalent to two linear equations
$\left\{ \begin{aligned} 4x + y &= 6x \\ 6x + 3y &= 6y\end{aligned} \right.$ that is $\left\{ \begin{aligned} -2x + y &= 0 \\ 6x - 3y &= 0\end{aligned} \right.$

Both equations reduce to the single linear equation $y=2x$. Therefore, any vector of the form $\begin{bmatrix} a & 2a \end{bmatrix}^\textsf{T}$, for any nonzero real number $a$, is an eigenvector of $A$ with eigenvalue $\lambda = 6$.

The matrix $A$ above has another eigenvalue $\lambda=1$. A similar calculation shows that the corresponding eigenvectors are the nonzero solutions of $3x+y=0$, that is, any vector of the form $\begin{bmatrix} b & -3b \end{bmatrix}^\textsf{T}$, for any nonzero real number $b$.

Simple iterative methods

The converse approach, of first seeking the eigenvectors and then determining each eigenvalue from its eigenvector, turns out to be far more tractable for computers. The easiest algorithm here consists of picking an arbitrary starting vector and then repeatedly multiplying it with the matrix (optionally normalizing the vector to keep its elements of reasonable size); this makes the vector converge towards an eigenvector. inverse iteration, A variation is to instead multiply the vector by this causes it to converge to an eigenvector of the eigenvalue closest to

If $\mathbf{v}$ is (a good approximation of) an eigenvector of $A$, then the corresponding eigenvalue can be computed as
: $\lambda = \frac{\mathbf{v}^* A\mathbf{v{\mathbf{v}^* \mathbf{v$

where $\mathbf{v}^*$ denotes the conjugate transpose of $\mathbf{v}$.

Modern methods

Efficient, accurate methods to compute eigenvalues and eigenvectors of arbitrary matrices were not known until the QR algorithm was designed in 1961. Combining the Householder transformation with the LU decomposition results in an algorithm with better convergence than the QR algorithm. For large Hermitian matrix, Hermitian sparse matrix, sparse matrices, the Lanczos algorithm is one example of an efficient iterative method to compute eigenvalues and eigenvectors, among several other possibilities.

Most numeric methods that compute the eigenvalues of a matrix also determine a set of corresponding eigenvectors as a by-product of the computation, although sometimes implementors choose to discard the eigenvector information as soon as it is no longer needed.

Applications

Eigenvalues of geometric transformations

The following table presents some example transformations in the plane along with their 2×2 matrices, eigenvalues, and eigenvectors.
{, class="wikitable" style="text-align:center; margin:1em auto 1em auto;"
, + Eigenvalues of geometric transformations
, -
!
! scope="col" , Scaling (geometry), Scaling
! scope="col" , Unequal scaling
! scope="col" , Rotation (geometry), Rotation
! scope="col" , Shear mapping, Horizontal shear
! scope="col" , Hyperbolic rotation
, -
! scope="row" , Illustration
,
,
,
,
,
, - style="vertical-align:top"
! scope="row" , Matrix
, $\begin{bmatrix}k & 0\\ 0 & k\end{bmatrix}$
, $\begin{bmatrix}k_1 & 0\\ 0 & k_2\end{bmatrix}$
, $\begin{bmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{bmatrix}$
, $\begin{bmatrix}1 & k\\ 0 & 1\end{bmatrix}$
, $\begin{bmatrix}\cosh\varphi & \sinh\varphi\\ \sinh\varphi & \cosh\varphi\end{bmatrix}$
, -
! scope="row" , Characteristic
polynomial
, $\ (\lambda - k)^2$
, $(\lambda - k_1)(\lambda - k_2)$
, $\lambda^2 - 2\cos(\theta)\lambda + 1$
, $\ (\lambda - 1)^2$
, $\lambda^2 - 2\cosh(\varphi)\lambda + 1$
, -
! scope="row" , Eigenvalues, $\lambda_i$
, $\lambda_1 = \lambda_2 = k$
, $\begin{align}\lambda_1 &= k_1 \\ \lambda_2 &= k_2\end{align}$
, $\begin{align}\lambda_1 &= e^{i\theta} \\ &= \cos\theta + i\sin\theta \\ \lambda_2 &= e^{-i\theta} \\ &= \cos\theta - i\sin\theta \end{align}$
, $\lambda_1 = \lambda_2 = 1$
, $\begin{align}\lambda_1 &= e^\varphi \\ &= \cosh\varphi + \sinh\varphi \\ \lambda_2 &= e^{-\varphi} \\ &= \cosh\varphi - \sinh\varphi \end{align}$
, -
! scope="row" , Algebraic ,
$\mu_i = \mu(\lambda_i)$
, $\mu_1 = 2$
, $\begin{align}\mu_1 &= 1 \\ \mu_2 &= 1 \end{align}$
, $\begin{align}\mu_1 &= 1 \\ \mu_2 &= 1 \end{align}$
, $\mu_1 = 2$
, $\begin{align}\mu_1 &= 1 \\ \mu_2 &= 1 \end{align}$
, -
! scope="row" , Geometric ,
$\gamma_i = \gamma(\lambda_i)$
, $\gamma_1 = 2$
, $\begin{align}\gamma_1 &= 1 \\ \gamma_2 &= 1 \end{align}$
, $\begin{align}\gamma_1 &= 1 \\ \gamma_2 &= 1 \end{align}$
, $\gamma_1 = 1$
, $\begin{align}\gamma_1 &= 1 \\ \gamma_2 &= 1 \end{align}$
, -
! scope="row" , Eigenvectors
, All nonzero vectors
, $\begin{align} \mathbf u_1 &= \begin{bmatrix} 1\\ 0\end{bmatrix} \\ \mathbf u_2 &= \begin{bmatrix} 0\\ 1\end{bmatrix} \end{align}$
, $\begin{align} \mathbf u_1 &= \begin{bmatrix} 1\\ -i\end{bmatrix} \\ \mathbf u_2 &= \begin{bmatrix} 1\\ +i\end{bmatrix} \end{align}$
, $\mathbf u_1 = \begin{bmatrix} 1\\ 0 \end{bmatrix}$
, $\begin{align} \mathbf u_1 &= \begin{bmatrix} 1\\ 1\end{bmatrix} \\ \mathbf u_2 &= \begin{bmatrix} 1\\ -1\end{bmatrix} \end{align}$

The characteristic equation for a rotation is a quadratic equation with discriminant $D = -4(\sin\theta)^2$, which is a negative number whenever is not an integer multiple of 180°. Therefore, except for these special cases, the two eigenvalues are complex numbers, $\cos\theta \pm i\sin\theta$; and all eigenvectors have non-real entries. Indeed, except for those special cases, a rotation changes the direction of every nonzero vector in the plane.

A linear transformation that takes a square to a rectangle of the same area (a squeeze mapping) has reciprocal eigenvalues.

Schrödinger equation

An example of an eigenvalue equation where the transformation $T$ is represented in terms of a differential operator is the time-independent Schrödinger equation in quantum mechanics:

: $H\psi_E = E\psi_E \,$

where $H$, the Hamiltonian (quantum mechanics), Hamiltonian, is a second-order differential operator and $\psi_E$, the wavefunction, is one of its eigenfunctions corresponding to the eigenvalue $E$, interpreted as its energy.

However, in the case where one is interested only in the bound state solutions of the Schrödinger equation, one looks for $\psi_E$ within the space of Square-integrable function, square integrable functions. Since this space is a Hilbert space with a well-defined scalar product, one can introduce a Basis (linear algebra), basis set in which $\psi_E$ and $H$ can be represented as a one-dimensional array (i.e., a vector) and a matrix respectively. This allows one to represent the Schrödinger equation in a matrix form.

The bra–ket notation is often used in this context. A vector, which represents a state of the system, in the Hilbert space of square integrable functions is represented by $, \Psi_E\rangle$. In this notation, the Schrödinger equation is:
: $H, \Psi_E\rangle = E, \Psi_E\rangle$

where $, \Psi_E\rangle$ is an eigenstate of $H$ and $E$ represents the eigenvalue. $H$ is an observable self-adjoint operator, the infinite-dimensional analog of Hermitian matrices. As in the matrix case, in the equation above $H, \Psi_E\rangle$ is understood to be the vector obtained by application of the transformation $H$ to $, \Psi_E\rangle$.

Wave transport

Light, acoustic waves, and microwaves are randomly Scattering theory, scattered numerous times when traversing a static disordered system. Even though multiple scattering repeatedly randomizes the waves, ultimately coherent wave transport through the system is a deterministic process which can be described by a field transmission matrix $\mathbf{t}$. The eigenvectors of the transmission operator $\mathbf{t}^\dagger\mathbf{t}$ form a set of disorder-specific input wavefronts which enable waves to couple into the disordered system's eigenchannels: the independent pathways waves can travel through the system. The eigenvalues, $\tau$, of $\mathbf{t}^\dagger\mathbf{t}$ correspond to the intensity transmittance associated with each eigenchannel. One of the remarkable properties of the transmission operator of diffusive systems is their bimodal eigenvalue distribution with $\tau_\max = 1$ and $\tau_\min = 0$. Furthermore, one of the striking properties of open eigenchannels, beyond the perfect transmittance, is the statistically robust spatial profile of the eigenchannels.

Molecular orbitals

In quantum mechanics, and in particular in atomic physics, atomic and molecular physics, within the Hartree–Fock theory, the atomic orbital, atomic and molecular orbitals can be defined by the eigenvectors of the Fock operator. The corresponding eigenvalues are interpreted as ionization potentials via Koopmans' theorem. In this case, the term eigenvector is used in a somewhat more general meaning, since the Fock operator is explicitly dependent on the orbitals and their eigenvalues. Thus, if one wants to underline this aspect, one speaks of nonlinear eigenvalue problems. Such equations are usually solved by an iteration procedure, called in this case self-consistent field method. In quantum chemistry, one often represents the Hartree–Fock equation in a non-orthogonal basis set (chemistry), basis set. This particular representation is a generalized eigenvalue problem called Roothaan equations.

Geology and glaciology

In geology, especially in the study of glacial till, eigenvectors and eigenvalues are used as a method by which a mass of information of a clast fabric's constituents' orientation and dip can be summarized in a 3-D space by six numbers. In the field, a geologist may collect such data for hundreds or thousands of clasts in a soil sample, which can only be compared graphically such as in a Tri-Plot (Sneed and Folk) diagram, or as a Stereonet on a Wulff Net.

The output for the orientation tensor is in the three orthogonal (perpendicular) axes of space. The three eigenvectors are ordered $\mathbf v_1, \mathbf v_2, \mathbf v_3$ by their eigenvalues $E_1 \geq E_2 \geq E_3$;
$\mathbf v_1$ then is the primary orientation/dip of clast, $\mathbf v_2$ is the secondary and $\mathbf v_3$ is the tertiary, in terms of strength. The clast orientation is defined as the direction of the eigenvector, on a compass rose of turn (geometry), 360°. Dip is measured as the eigenvalue, the modulus of the tensor: this is valued from 0° (no dip) to 90° (vertical). The relative values of $E_1$, $E_2$, and $E_3$ are dictated by the nature of the sediment's fabric. If $E_1 = E_2 = E_3$, the fabric is said to be isotropic. If $E_1 = E_2 > E_3$, the fabric is said to be planar. If $E_1 > E_2 > E_3$, the fabric is said to be linear.

Principal component analysis

The Eigendecomposition of a matrix#Real symmetric matrices, eigendecomposition of a symmetric matrix, symmetric positive semidefinite matrix, positive semidefinite (PSD) positive semidefinite matrix, matrix yields an orthogonal basis of eigenvectors, each of which has a nonnegative eigenvalue. The orthogonal decomposition of a PSD matrix is used in multivariate statistics, multivariate analysis, where the sample variance, sample covariance matrix, covariance matrices are PSD. This orthogonal decomposition is called principal component analysis (PCA) in statistics. PCA studies linear relations among variables. PCA is performed on the covariance matrix or the correlation matrix (in which each variable is scaled to have its sample variance equal to one). For the covariance or correlation matrix, the eigenvectors correspond to principal component analysis, principal components and the eigenvalues to the explained variance, variance explained by the principal components. Principal component analysis of the correlation matrix provides an orthogonal basis for the space of the observed data: In this basis, the largest eigenvalues correspond to the principal components that are associated with most of the covariability among a number of observed data.

Principal component analysis is used as a means of dimensionality reduction in the study of large data sets, such as those encountered in bioinformatics. In Q methodology, the eigenvalues of the correlation matrix determine the Q-methodologist's judgment of ''practical'' significance (which differs from the statistical significance of hypothesis testing; cf. Scree's test, criteria for determining the number of factors). More generally, principal component analysis can be used as a method of factor analysis in structural equation modeling.

Vibration analysis

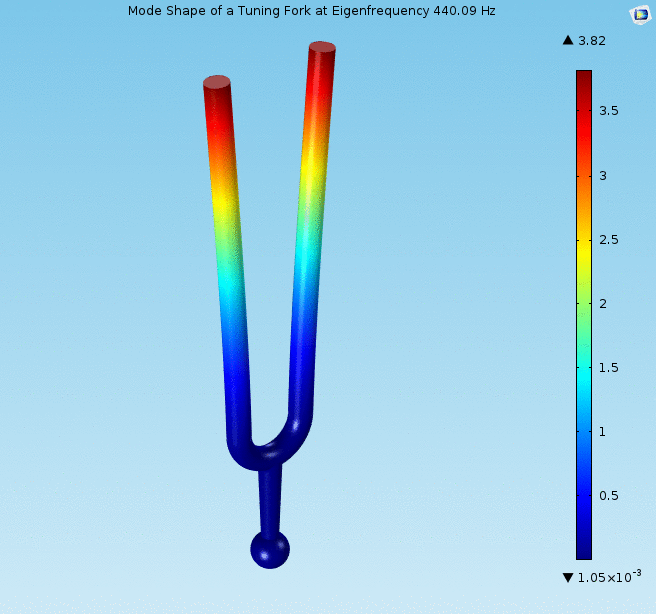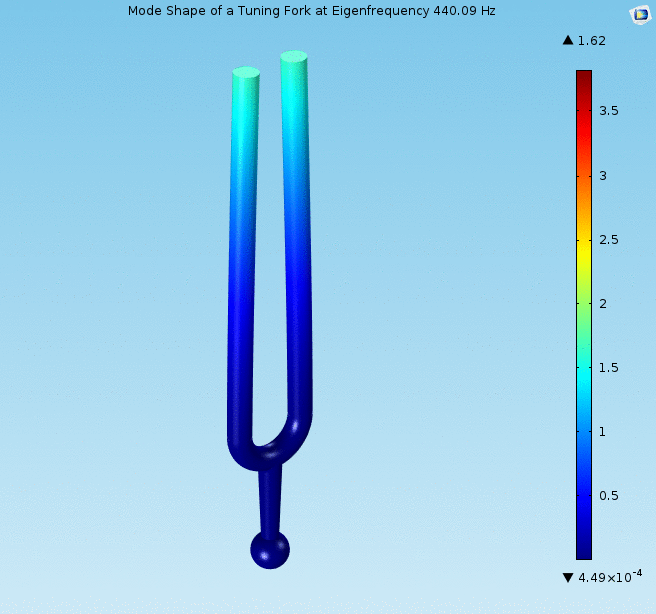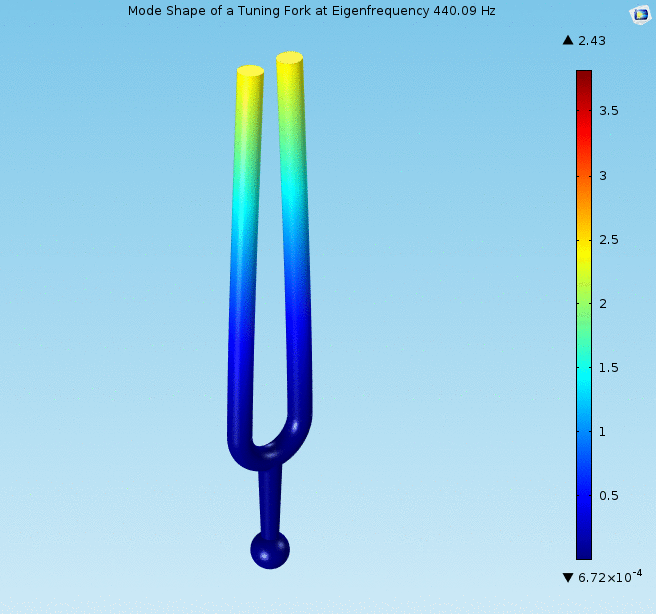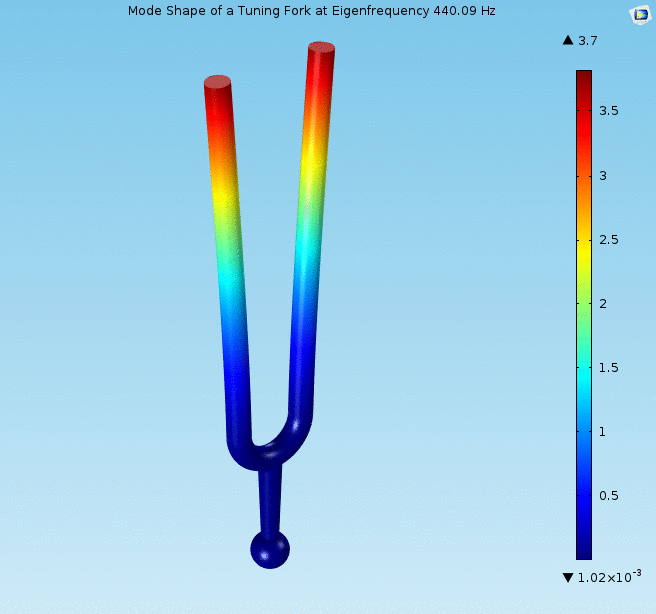
Eigenvalue problems occur naturally in the vibration analysis of mechanical structures with many Degrees of freedom (mechanics), degrees of freedom. The eigenvalues are the natural frequencies (or eigenfrequencies) of vibration, and the eigenvectors are the shapes of these vibrational modes. In particular, undamped vibration is governed by
$m\ddot{x} + kx = 0$

or
$m\ddot{x} = -kx$

that is, acceleration is proportional to position (i.e., we expect $x$ to be sinusoidal in time).

In $n$ dimensions, $m$ becomes a mass matrix and $k$ a stiffness matrix. Admissible solutions are then a linear combination of solutions to the generalized eigenvalue problem
$kx = \omega^2 mx$

where $\omega^2$ is the eigenvalue and $\omega$ is the (imaginary) angular frequency. The principal vibration modes are different from the principal compliance modes, which are the eigenvectors of $k$ alone. Furthermore, damped vibration, governed by
$m\ddot{x} + c\dot{x} + kx = 0$

leads to a so-called quadratic eigenvalue problem,
$\left(\omega^2 m + \omega c + k\right)x = 0.$

This can be reduced to a generalized eigenvalue problem by quadratic eigenvalue problem#Methods of Solution, algebraic manipulation at the cost of solving a larger system.

The orthogonality properties of the eigenvectors allows decoupling of the differential equations so that the system can be represented as linear summation of the eigenvectors. The eigenvalue problem of complex structures is often solved using finite element analysis, but neatly generalize the solution to scalar-valued vibration problems.

Eigenfaces

In image processing, processed images of faces can be seen as vectors whose components are the brightnesses of each pixel. The dimension of this vector space is the number of pixels. The eigenvectors of the covariance matrix associated with a large set of normalized pictures of faces are called eigenfaces; this is an example of principal component analysis. They are very useful for expressing any face image as a linear combination of some of them. In the Facial recognition system, facial recognition branch of biometrics, eigenfaces provide a means of applying data compression to faces for Recognition of human individuals, identification purposes. Research related to eigen vision systems determining hand gestures has also been made.

Similar to this concept, eigenvoices represent the general direction of variability in human pronunciations of a particular utterance, such as a word in a language. Based on a linear combination of such eigenvoices, a new voice pronunciation of the word can be constructed. These concepts have been found useful in automatic speech recognition systems for speaker adaptation.

Tensor of moment of inertia

In mechanics, the eigenvectors of the inertia tensor, moment of inertia tensor define the principal axes of a rigid body. The tensor of moment of inertia is a key quantity required to determine the rotation of a rigid body around its center of mass.

Stress tensor

In solid mechanics, the stress (mechanics), stress tensor is symmetric and so can be decomposed into a diagonal tensor with the eigenvalues on the diagonal and eigenvectors as a basis. Because it is diagonal, in this orientation, the stress tensor has no Shear (mathematics), shear components; the components it does have are the principal components.

Graphs

In spectral graph theory, an eigenvalue of a graph theory, graph is defined as an eigenvalue of the graph's adjacency matrix $A$, or (increasingly) of the graph's Laplacian matrix due to its discrete Laplace operator, which is either $D - A$ (sometimes called the ''combinatorial Laplacian'') or $I - D^{-1/2}A D^{-1/2}$ (sometimes called the ''normalized Laplacian''), where $D$ is a diagonal matrix with $D_{ii}$ equal to the degree of vertex $v_i$, and in $D^{-1/2}$, the $i$th diagonal entry is $1/\sqrt{\deg(v_i)}$. The $k$th principal eigenvector of a graph is defined as either the eigenvector corresponding to the $k$th largest or $k$th smallest eigenvalue of the Laplacian. The first principal eigenvector of the graph is also referred to merely as the principal eigenvector.

The principal eigenvector is used to measure the eigenvector centrality, centrality of its vertices. An example is Google's PageRank algorithm. The principal eigenvector of a modified adjacency matrix of the World Wide Web graph gives the page ranks as its components. This vector corresponds to the stationary distribution of the Markov chain represented by the row-normalized adjacency matrix; however, the adjacency matrix must first be modified to ensure a stationary distribution exists. The second smallest eigenvector can be used to partition the graph into clusters, via spectral clustering. Other methods are also available for clustering.

Basic reproduction number

The basic reproduction number ($R_0$) is a fundamental number in the study of how infectious diseases spread. If one infectious person is put into a population of completely susceptible people, then $R_0$ is the average number of people that one typical infectious person will infect. The generation time of an infection is the time, $t_G$, from one person becoming infected to the next person becoming infected. In a heterogeneous population, the next generation matrix defines how many people in the population will become infected after time $t_G$ has passed. $R_0$ is then the largest eigenvalue of the next generation matrix.

See also

* Antieigenvalue theory
* Eigenoperator
* Eigenplane
* Eigenmoments
* Eigenvalue algorithm
* Introduction to eigenstates
* Jordan normal form
* List of numerical-analysis software
* Nonlinear eigenproblem
* Normal eigenvalue
* Quadratic eigenvalue problem
* Singular value
* Spectrum of a matrix

Notes

Citations

Sources

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*

Further reading

*
*
*
*
*

External links

What are Eigen Values?
– non-technical introduction from PhysLink.com's "Ask the Experts"


– Tutorial and Interactive Program from Revoledu.

Introduction to Eigen Vectors and Eigen Values
– lecture from Khan Academy

Eigenvectors and eigenvalues , Essence of linear algebra, chapter 10
– A visual explanation with 3Blue1Brown

Matrix Eigenvectors Calculator
from Symbolab (Click on the bottom right button of the 2x12 grid to select a matrix size. Select an $n \times n$ size (for a square matrix), then fill out the entries numerically and click on the Go button. It can accept complex numbers as well.)

Theory

Edited by Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst

{{DEFAULTSORT:Eigenvalues And Eigenvectors
Abstract algebra
Linear algebra
Mathematical physics
Matrix theory
Singular value decomposition