|
Eigenfunction
In mathematics, an eigenfunction of a linear operator ''D'' defined on some function space is any non-zero function f in that space that, when acted upon by ''D'', is only multiplied by some scaling factor called an eigenvalue. As an equation, this condition can be written as Df = \lambda f for some scalar eigenvalue \lambda. The solutions to this equation may also be subject to boundary conditions that limit the allowable eigenvalues and eigenfunctions. An eigenfunction is a type of eigenvector. Eigenfunctions In general, an eigenvector of a linear operator ''D'' defined on some vector space is a nonzero vector in the domain of ''D'' that, when ''D'' acts upon it, is simply scaled by some scalar value called an eigenvalue. In the special case where ''D'' is defined on a function space, the eigenvectors are referred to as eigenfunctions. That is, a function ''f'' is an eigenfunction of ''D'' if it satisfies the equation where λ is a scalar. The solutions to Equation may also ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hilbert Space
In mathematics, Hilbert spaces (named after David Hilbert) allow generalizing the methods of linear algebra and calculus from (finite-dimensional) Euclidean vector spaces to spaces that may be infinite-dimensional. Hilbert spaces arise naturally and frequently in mathematics and physics, typically as function spaces. Formally, a Hilbert space is a vector space equipped with an inner product that defines a distance function for which the space is a complete metric space. The earliest Hilbert spaces were studied from this point of view in the first decade of the 20th century by David Hilbert, Erhard Schmidt, and Frigyes Riesz. They are indispensable tools in the theories of partial differential equations, quantum mechanics, Fourier analysis (which includes applications to signal processing and heat transfer), and ergodic theory (which forms the mathematical underpinning of thermodynamics). John von Neumann coined the term ''Hilbert space'' for the abstract concept that under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthonormal Basis
In mathematics, particularly linear algebra, an orthonormal basis for an inner product space ''V'' with finite dimension is a basis for V whose vectors are orthonormal, that is, they are all unit vectors and orthogonal to each other. For example, the standard basis for a Euclidean space \R^n is an orthonormal basis, where the relevant inner product is the dot product of vectors. The image of the standard basis under a rotation or reflection (or any orthogonal transformation) is also orthonormal, and every orthonormal basis for \R^n arises in this fashion. For a general inner product space V, an orthonormal basis can be used to define normalized orthogonal coordinates on V. Under these coordinates, the inner product becomes a dot product of vectors. Thus the presence of an orthonormal basis reduces the study of a finite-dimensional inner product space to the study of \R^n under dot product. Every finite-dimensional inner product space has an orthonormal basis, which may be ob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eigenvalues And Eigenvectors
In linear algebra, an eigenvector () or characteristic vector of a linear transformation is a nonzero vector that changes at most by a scalar factor when that linear transformation is applied to it. The corresponding eigenvalue, often denoted by \lambda, is the factor by which the eigenvector is scaled. Geometrically, an eigenvector, corresponding to a real nonzero eigenvalue, points in a direction in which it is stretched by the transformation and the eigenvalue is the factor by which it is stretched. If the eigenvalue is negative, the direction is reversed. Loosely speaking, in a multidimensional vector space, the eigenvector is not rotated. Formal definition If is a linear transformation from a vector space over a field into itself and is a nonzero vector in , then is an eigenvector of if is a scalar multiple of . This can be written as T(\mathbf) = \lambda \mathbf, where is a scalar in , known as the eigenvalue, characteristic value, or characteristic root ass ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although note that in quantum mechanics, A^\ast typically means the complex conjugate only, and not the conjugate transpose. Alternative characterizations Hermit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirac Delta Function
In mathematics, the Dirac delta distribution ( distribution), also known as the unit impulse, is a generalized function or distribution over the real numbers, whose value is zero everywhere except at zero, and whose integral over the entire real line is equal to one. The current understanding of the unit impulse is as a linear functional that maps every continuous function (e.g., f(x)) to its value at zero of its domain (f(0)), or as the weak limit of a sequence of bump functions (e.g., \delta(x) = \lim_ \frace^), which are zero over most of the real line, with a tall spike at the origin. Bump functions are thus sometimes called "approximate" or "nascent" delta distributions. The delta function was introduced by physicist Paul Dirac as a tool for the normalization of state vectors. It also has uses in probability theory and signal processing. Its validity was disputed until Laurent Schwartz developed the theory of distributions where it is defined as a linear form acting on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sturm–Liouville Theory
In mathematics and its applications, classical Sturm–Liouville theory is the theory of ''real'' second-order ''linear'' ordinary differential equations of the form: for given coefficient functions , , and , an unknown function ''y = y''(''x'') of the free variable , and an unknown constant λ. All homogeneous (i.e. with the right-hand side equal to zero) second-order linear ordinary differential equations can be reduced to this form. In addition, the solution is typically required to satisfy some boundary conditions at extreme values of ''x''. Each such equation () together with its boundary conditions constitutes a Sturm–Liouville problem. In the simplest case where all coefficients are continuous on the finite closed interval and has continuous derivative, a function ''y = y''(''x'') is called a ''solution'' if it is continuously differentiable and satisfies the equation () at every x\in (a,b). In the case of more general , , , the solutions must be understood in a weak ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Drum Vibration Mode12
The drum is a member of the percussion group of musical instruments. In the Hornbostel-Sachs classification system, it is a membranophone. Drums consist of at least one membrane, called a drumhead or drum skin, that is stretched over a shell and struck, either directly with the player's hands, or with a percussion mallet, to produce sound. There is usually a resonant head on the underside of the drum. Other techniques have been used to cause drums to make sound, such as the thumb roll. Drums are the world's oldest and most ubiquitous musical instruments, and the basic design has remained virtually unchanged for thousands of years. Drums may be played individually, with the player using a single drum, and some drums such as the djembe are almost always played in this way. Others are normally played in a set of two or more, all played by the one player, such as bongo drums and timpani. A number of different drums together with cymbals form the basic modern drum kit. Uses ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
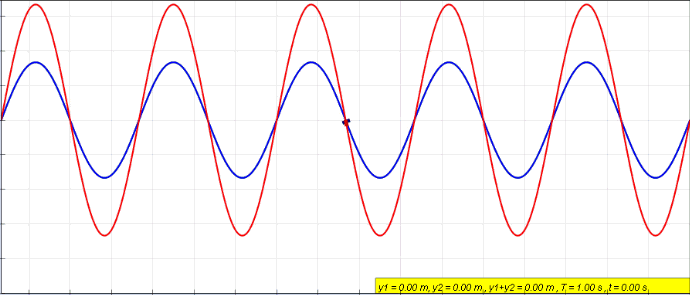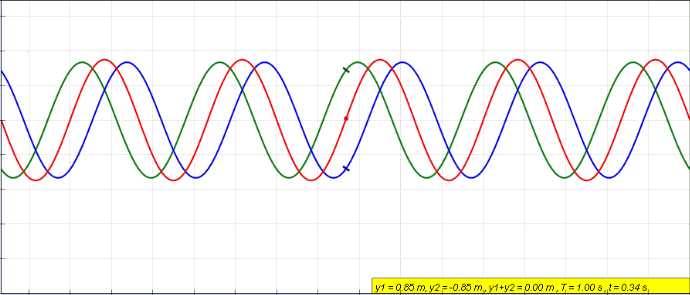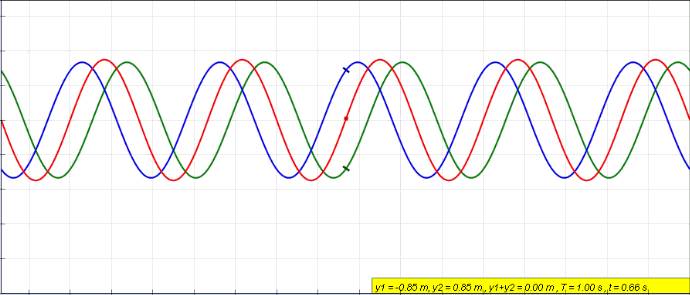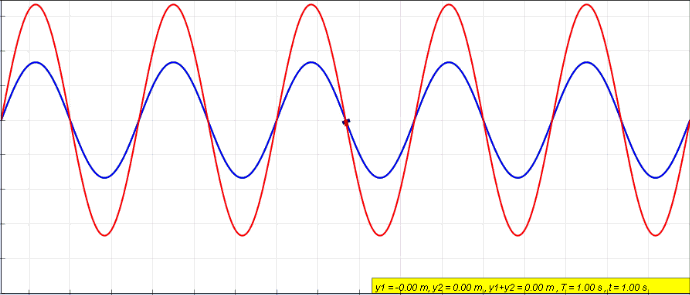
Standing Wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect to time, and the oscillations at different points throughout the wave are in phase. The locations at which the absolute value of the amplitude is minimum are called nodes, and the locations where the absolute value of the amplitude is maximum are called antinodes. Standing waves were first noticed by Michael Faraday in 1831. Faraday observed standing waves on the surface of a liquid in a vibrating container. Franz Melde coined the term "standing wave" (German: ''stehende Welle'' or ''Stehwelle'') around 1860 and demonstrated the phenomenon in his classic experiment with vibrating strings. This phenomenon can occur because the medium is moving in the direction opposite to the movement of the wave, or it can arise in a stationary medium ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Self-adjoint Operator
In mathematics, a self-adjoint operator on an infinite-dimensional complex vector space ''V'' with inner product \langle\cdot,\cdot\rangle (equivalently, a Hermitian operator in the finite-dimensional case) is a linear map ''A'' (from ''V'' to itself) that is its own adjoint. If ''V'' is finite-dimensional with a given orthonormal basis, this is equivalent to the condition that the matrix of ''A'' is a Hermitian matrix, i.e., equal to its conjugate transpose ''A''. By the finite-dimensional spectral theorem, ''V'' has an orthonormal basis such that the matrix of ''A'' relative to this basis is a diagonal matrix with entries in the real numbers. In this article, we consider generalizations of this concept to operators on Hilbert spaces of arbitrary dimension. Self-adjoint operators are used in functional analysis and quantum mechanics. In quantum mechanics their importance lies in the Dirac–von Neumann formulation of quantum mechanics, in which physical observables such as positi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
String Instrument
String instruments, stringed instruments, or chordophones are musical instruments that produce sound from vibrating strings when a performer plays or sounds the strings in some manner. Musicians play some string instruments by plucking the strings with their fingers or a plectrum—and others by hitting the strings with a light wooden hammer or by rubbing the strings with a bow. In some keyboard instruments, such as the harpsichord, the musician presses a key that plucks the string. Other musical instruments generate sound by striking the string. With bowed instruments, the player pulls a rosined horsehair bow across the strings, causing them to vibrate. With a hurdy-gurdy, the musician cranks a wheel whose rosined edge touches the strings. Bowed instruments include the string section instruments of the orchestra in Western classical music (violin, viola, cello and double bass) and a number of other instruments (e.g., viols and gambas used in early music from the Baro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |