Wave Packet (dispersion)

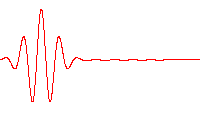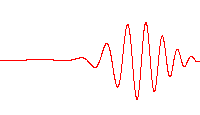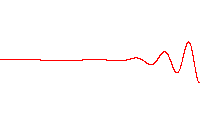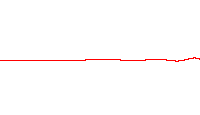
In physics, a wave packet (or wave train) is a short "burst" or "envelope" of localized wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere constructively only over a small region of space, and destructively elsewhere.
Each component wave function, and hence the wave packet, are solutions of a wave equation. Depending on the wave equation, the wave packet's profile may remain constant (no dispersion, see figure) or it may change (dispersion) while propagating.

Quantum mechanics ascribes a special significance to the wave packet; it is interpreted as a probability amplitude, its norm squared describing the probability density that a particle or particles in a particular state will be measured to have a given position or momentum. The wave equation is in this case the Schrödinger equation, and through its application it is possible to deduce the time evolution of a quantum mechanical system, similar to the process of the Hamiltonian formalism in classical mechanics. The dispersive character of solutions of the Schrödinger equation has played an important role in rejecting Schrödinger's original interpretation, and accepting the Born rule.

In the coordinate representation of the wave (such as the Cartesian coordinate system), the position of the physical object's localized probability is specified by the position of the packet solution. Moreover, the narrower the spatial wave packet, and therefore the better localized the position of the wave packet, the larger the spread in the momentum of the wave. This trade-off between spread in position and spread in momentum is a characteristic feature of the Heisenberg uncertainty principle,
and will be illustrated below.

Historical background

In the early 1900s, it became apparent that classical mechanics had some major failings. Isaac Newton originally proposed the idea that light came in discrete packets, which he called corpuscles, but the wave-like behavior of many light phenomena quickly led scientists to favor a wave description of electromagnetism. It wasn't until the 1930s that the particle nature of light really began to be widely accepted in physics. The development of quantum mechanicsand its success at explaining confusing experimental resultswas at the root of this acceptance. Thus, one of the basic concepts in the formulation of quantum mechanics is that of light coming in discrete bundles called photons. The energy of a photon is a function of its frequency,
$E = h\nu.$
The photon's energy is equal to Planck's constant, , multiplied by its frequency, . This resolved a problem in classical physics, called the ultraviolet catastrophe.

The ideas of quantum mechanics continued to be developed throughout the 20th century. The picture that was developed was of a particulate world, with all phenomena and matter made of and interacting with discrete particles; however, these particles were described by a probability wave. The interactions, locations, and all of physics would be reduced to the calculations of these probability amplitudes.

The particle-like nature of the world has been confirmed by experiment over a century, while the wave-like phenomena could be characterized as consequences of the wave packet aspect of quantum particles (see wave-particle duality). According to the principle of complementarity, the wave-like and particle-like characteristics never manifest themselves at the same time, i.e., in the same experiment; see, however, the Afshar experiment and the lively discussion around it.

Basic behaviors

Non-dispersive

As an example of propagation ''without dispersion'', consider wave solutions to the following wave equation from classical physics
$= c^2 \, \nabla^2 u,$

where is the speed of the wave's propagation in a given medium.

Using the physics time convention, , the wave equation has plane-wave solutions
$u(\mathbf,t) = e^,$

where
$\omega^2 =, \mathbf, ^2 c^2,$ and $, \mathbf, ^2 = k_x^2 + k_y^2+ k_z^2.$

This relation between and should be valid so that the plane wave is a solution to the wave equation. It is called a dispersion relation.

To simplify, consider only waves propagating in one dimension (extension to three dimensions is straightforward). Then the general solution is
$u(x,t)= A e^ + B e^,$
in which we may take . The first term represents a wave propagating in the positive since it is a function of only; the second term, being a function of , represents a wave propagating in the negative .

A wave packet is a localized disturbance that results from the sum of many different wave forms. If the packet is strongly localized, more frequencies are needed to allow the constructive superposition in the region of localization and destructive superposition outside the region. From the basic solutions in one dimension, a general form of a wave packet can be expressed as
$u(x,t) = \frac \int^_ A(k) ~ e^ \, dk.$

As in the plane-wave case the wave packet travels to the right for , since , and to the left for , since .

The factor comes from Fourier transform conventions. The amplitude contains the coefficients of the linear superposition of the plane-wave solutions. These coefficients can in turn be expressed as a function of evaluated at by inverting the Fourier transform relation above:
$A(k) = \frac \int^_ u(x,0) ~ e^ \, dx.$

For instance, choosing
$u(x,0) = e^,$

we obtain
$A(k) = \frac e^,$

and finally
\begin
u(x,t) &= e^\\
&= e^ \left cos\left(2\pi \frac\right)+ i\sin\left(2\pi\frac\right)\right
\end

The nondispersive propagation of the real or imaginary part of this wave packet is presented in the above animation.

Dispersive

By contrast, as an example of propagation now ''with dispersion'', consider instead solutions to the Schrödinger equation (nondimensionalized with , , and ''ħ'' set equal to one),
$i = -\frac ,$
yielding the dispersion relation
$\omega = \frac, \mathbf, ^2.$

Once again, restricting attention to one dimension, the solution to the Schrödinger equation satisfying the initial condition \psi(x,0)= \sqrt \exp\left(\right), representing a wave packet localized in space at the origin, is seen to be
$\begin \psi(x,t) &= \frac e^ ~ e^\\ &= \frac e^~ e^ ~. \end$

An impression of the dispersive behavior of this wave packet is obtained by looking at the probability density:
$, \psi(x,t), ^2 = \frac~e^~.$
It is evident that this dispersive wave packet, while moving with constant group velocity , is delocalizing rapidly: it has a width increasing with time as , so eventually it diffuses to an unlimited region of space.By contrast, the introduction of ''interaction terms'' in dispersive equations, such as for the quantum harmonic oscillator, may result in the emergence of envelope-non-dispersive, classical-looking solutions—see coherent states: Such "minimum uncertainty states" do saturate the uncertainty principle permanently.

The momentum profile remains invariant. The probability current is
$j=\rho v = \frac (\psi^* \nabla \psi - \psi \nabla \psi^*)= \rho \left (k_0+\frac\right ) .$

Gaussian wave packets in quantum mechanics

The above dispersive Gaussian wave packet, unnormalized and just centered at the origin, instead, at =0, can now be written in 3D, now in standard units:
$\psi(\mathbf,0) = e^,$
where is a positive real number, the ''square of the width of the wave packet'',
$a = 2\langle \mathbf r \cdot \mathbf r\rangle/3\langle 1\rangle = 2 (\Delta x)^2.$

The Fourier transform is also a Gaussian in terms of the wavenumber, =0,
the k-vector, (with inverse width,
$1/a = 2\langle\mathbf k\cdot \mathbf k\rangle/3\langle 1\rangle = 2 (\Delta p_x/\hbar)^2,$
so that
$\Delta x \Delta p_x = \hbar/2,$
i.e., it saturates the uncertainty relation),
$\psi(\mathbf,0) = (2\pi a)^ e^.$

Each separate wave only phase-rotates in time, so that the time dependent Fourier-transformed solution is

The inverse Fourier transform is still a Gaussian, but now the parameter has become complex, and there is an overall normalization factor.

The integral of over all space is invariant, because it is the inner product of with the state of zero energy, which is a wave with infinite wavelength, a constant function of space. For any energy eigenstate , the inner product,
$\langle \eta , \psi \rangle = \int \eta(\mathbf) \psi(\mathbf)d^3\mathbf,$
only changes in time in a simple way: its phase rotates with a frequency determined by the energy of . When has zero energy, like the infinite wavelength wave, it doesn't change at all.

The integral is also invariant, which is a statement of the conservation of probability. Explicitly,

in which is the width of at ; is the distance from the origin; the speed of the particle is zero; and the time origin can be chosen arbitrarily.

The width of the Gaussian is the interesting quantity which can be read off from the probability density, ,

$\sqrt.$
This width eventually grows linearly in time, as , indicating wave-packet spreading.

For example, if an electron wave packet is initially localized in a region of atomic dimensions (i.e., m) then the width of the packet doubles in about s. Clearly, particle wave packets spread out very rapidly indeed (in free space): For instance, after ms, the width will have grown to about a kilometer.

This linear growth is a reflection of the (time-invariant) momentum uncertainty: the wave packet is confined to a narrow , and so has a momentum which is uncertain (according to the uncertainty principle) by the amount , a spread in velocity of , and thus in the future position by . The uncertainty relation is then a strict inequality, very far from saturation, indeed! The initial uncertainty has now increased by a factor of (for large ).

The Airy wave train

In contrast to the above Gaussian wave packet, it has been observed that a particular wave
function based on Airy functions, propagates freely without envelope dispersion, maintaining its shape. It accelerates undistorted in the absence of a force field: . (For simplicity, , , and ''B'' is a constant, cf. nondimensionalization.)

Nevertheless, there is no dissonance with Ehrenfest's theorem in this force-free situation, because the state is both non-normalizable and has an undefined (infinite) for all times. (To the extent that it could be defined, for all times, despite the apparent acceleration of the front.)

In phase space, this is evident in the pure state Wigner quasiprobability distribution of this wavetrain, whose shape in ''x'' and ''p'' is invariant as time progresses, but whose features accelerate to the right, in accelerating parabolas ,
$W(x,p;t) = W(x-B^3 t^2, p-B^3 t ;0) = ~ \mathrm \left(2^ \left(Bx + - 2Bpt\right)\right).$

Note the momentum distribution obtained by integrating over all is constant. Since this is the probability density in momentum space, it is evident that the wave function itself is not normalizable.

In 2018, the first experimental observation of the cubic phase of accelerating Airy wave packets was achieved by a collaboration of researchers from Israeli, German, and American universities.

Free propagator

The narrow-width limit of the Gaussian wave packet solution discussed is the free ''propagator kernel'' . For other differential equations, this is usually called the Green's function, but in quantum mechanics it is traditional to reserve the name Green's function for the time Fourier transform of .

Returning to one dimension for simplicity, with ''m'' and ħ set equal to one, when is the infinitesimal quantity , the Gaussian initial condition, rescaled so that its integral is one,
$\psi_0(x) = e^ \,$
becomes a delta function, , so that its time evolution,
$K_t(x) = e^\,$
yields the propagator.

Note that a very narrow initial wave packet instantly becomes infinitely wide, but with a phase which is more rapidly oscillatory at large values of ''x''. This might seem strange—the solution goes from being localized at one point to being "everywhere" at ''all later times'', but it is a reflection of the enormous momentum uncertainty of a localized particle, as explained above.

Further note that the norm of the wave function is infinite, which is also correct, since the square of a delta function is divergent in the same way.

The factor involving is an infinitesimal quantity which is there to make sure that integrals over are well defined. In the limit that , becomes purely oscillatory, and integrals of are not absolutely convergent. In the remainder of this section, it ''will'' be set to zero, but in order for all the integrations over intermediate states to be well defined, the limit ''ε''→0 is to be only taken after the final state is calculated.

The propagator is the amplitude for reaching point ''x'' at time ''t'', when starting at the origin, ''x''=0. By translation invariance, the amplitude for reaching a point ''x'' when starting at point ''y'' is the same function, only now translated,
$K_t(x,y) = K_t(x-y) = e^ \, .$

In the limit when ''t'' is small, the propagator goes to a delta function
$\lim_ K_t(x-y) = \delta(x-y) ~,$
but only in the sense of distributions: The integral of this quantity multiplied by an arbitrary differentiable test function gives the value of the test function at zero.

To see this, note that the integral over all space of equals 1 at all times,
$\int K_t(x) dx = 1 \, ,$
since this integral is the inner-product of ''K'' with the uniform wave function. But the phase factor in the exponent has a nonzero spatial derivative everywhere except at the origin, and so when the time is small there are fast phase cancellations at all but one point. This is rigorously true when the limit ''ε''→0 is taken at the very end.

So the propagation kernel is the (future) time evolution of a delta function, and it is continuous, in a sense: it goes to the initial delta function at small times. If the initial wave function is an infinitely narrow spike at position ,
$\psi_0(x) = \delta(x - y) \, ,$
it becomes the oscillatory wave,
$\psi_t(x) = e^ \, .$

Now, since every function can be written as a weighted sum of such narrow spikes,
$\psi_0(x) = \int \psi_0(y) \delta(x-y) dy \, ,$
the time evolution of ''every function'' ₀ is determined by this propagation kernel ,

Thus, this is a formal way to express the fundamental solution or ''general solution''. The interpretation of this expression is that the amplitude for a particle to be found at point at time is the amplitude that it started at , times the amplitude that it went from to , ''summed over all the possible starting points''. In other words, it is a convolution of the kernel with the arbitrary initial condition ,
$\psi_t = K * \psi_0 \, .$

Since the amplitude to travel from to after a time +' can be considered in two steps, the propagator obeys the composition identity,
$\int K(x-y;t)K(y-z;t')dy = K(x-z;t+t')~ ,$
which can be interpreted as follows: the amplitude to travel from to in time +' is the sum of the amplitude to travel from to in time , multiplied by the amplitude to travel from to in time ', summed over ''all possible intermediate states y''. This is a property of an arbitrary quantum system, and by subdividing the time into many segments, it allows the time evolution to be expressed as a path integral.

Analytic continuation to diffusion

The spreading of wave packets in quantum mechanics is directly related to the spreading of probability densities in diffusion. For a particle which is randomly walking, the probability density function at any point satisfies the diffusion equation (also see the heat equation),
$\rho = \rho ~,$
where the factor of 2, which can be removed by rescaling either time or space, is only for convenience.

A solution of this equation is the spreading Gaussian,
$\rho_t(x) = e^ ~,$
and, since the integral of ''ρ_t'' is constant while the width is becoming narrow at small times, this function approaches a delta function at ''t''=0,
$\lim_ \rho_t(x) = \delta(x)$
again only in the sense of distributions, so that
$\lim_ \int_x f(x) \rho_t(x) = f(0)$
for any smooth test function .

The spreading Gaussian is the propagation kernel for the diffusion equation and it obeys the convolution identity,
$K_ = K_*K_ \, ,$
which allows diffusion to be expressed as a path integral. The propagator is the exponential of an operator ,
$K_t(x) = e^ \, ,$
which is the infinitesimal diffusion operator,
$H= - \, .$

A matrix has two indices, which in continuous space makes it a function of and '. In this case, because of translation invariance, the matrix element only depend on the difference of the position, and a convenient abuse of notation is to refer to the operator, the matrix elements, and the function of the difference by the same name:
$K_t(x,x') = K_t(x-x') \, .$

Translation invariance means that continuous matrix multiplication,
$C(x,x'') = \int_ A(x,x')B(x',x'') \, ,$
is essentially convolution,
$C(\Delta) = C(x-x'') = \int_ A(x-x') B(x'-x'') = \int_ A(\Delta-y)B(y) \, .$

The exponential can be defined over a range of ''t''s which include complex values, so long as integrals over the propagation kernel stay convergent,
$K_z(x) = e^ \, .$
As long as the real part of is positive, for large values of , is exponentially decreasing, and integrals over are indeed absolutely convergent.

The limit of this expression for approaching the pure imaginary axis is the above Schrödinger propagator encountered,
$K_t^ = K_ = e^ \, ,$
which illustrates the above time evolution of Gaussians.

From the fundamental identity of exponentiation, or path integration,
$K_z * K_ = K_ \,$
holds for all complex ''z'' values, where the integrals are absolutely convergent so that the operators are well defined.

Thus, quantum evolution of a Gaussian, which is the complex diffusion kernel ''K'',
$\psi_0(x) = K_a(x) = K_a * \delta(x) \,$
amounts to the time-evolved state,
$\psi_t = K_ * K_a = K_ \, .$

This illustrates the above diffusive form of the complex Gaussian solutions,
$\psi_t(x) = e^ \, .$

See also

*Wave
*Wave propagation
* Fourier analysis
* Group velocity
* Phase velocity
*Free particle
*Coherent states
*Waveform
*Wavelet
*Matter wave
*Schrödinger equation
*Introduction to quantum mechanics
*Soliton

Remarks

Notes

References

* This annus mirabilis paper on the photoelectric effect was received by ''Annalen der Physik'' 18 March 1905.
*
*
*
*
*
*
*
* (Dover, 2010, .)
*

External links

*
*

1d Wave packet plot in Google

1d Wave train and probability density plot in Google

2d Wave packet plot in Google

2d Wave train plot in Google

2d probability density plot in Google

Quantum physics online : Interactive simulation of a free wavepacket



Interactive 2D wave packet dynamics simulation

A simulation of a wave package in 2D (According to FOURIER-Synthesis in 2D)
* {{Citation, last=Curtfirst=T.L., url=http://www.physics.miami.edu/~curtright/TimeDependentWignerFunctions.html, title=Time-dependent Wigner Functions

Wave mechanics
Quantum mechanics