Weyr canonical form

In mathematics, in linear algebra, a Weyr canonical form (or, Weyr form or Weyr matrix) is a square matrix satisfying certain conditions. A square matrix is said to be ''in'' the Weyr canonical form if the matrix satisfies the conditions defining the Weyr canonical form. The Weyr form was discovered by the Czech mathematician Eduard Weyr in 1885. The Weyr form did not become popular among mathematicians and it was overshadowed by the closely related, but distinct, canonical form known by the name Jordan canonical form. The Weyr form has been rediscovered several times since Weyr’s original discovery in 1885. This form has been variously called as ''modified Jordan form,'' ''reordered Jordan form,'' ''second Jordan form,'' and ''H-form''. The current terminology is credited to Shapiro who introduced it in a paper published in the American Mathematical Monthly in 1999.

Recently several applications have been found for the Weyr matrix. Of particular interest is an application of the Weyr matrix in the study of phylogenetic invariants in biomathematics.

Definitions

Basic Weyr matrix

Definition

A basic Weyr matrix with eigenvalue $\lambda$ is an $n\times n$ matrix $W$ of the following form: There is a partition
: $n_1 + n_2+ \cdots +n_r=n$ of $n$ with $n_1\ge n_2\ge \cdots \ge n_r\ge 1$
such that, when $W$ is viewed as an $r \times r$ block matrix $(W_)$, where the $(i, j)$ block $W_$ is an $n_i \times n_j$ matrix, the following three features are present:
# The main diagonal blocks $W_$ are the $n_i\times n_i$ scalar matrices $\lambda I$ for $i = 1, \ldots , r$.
# The first superdiagonal blocks $W_$ are full column rank $n_i \times n_$ matrices in reduced row-echelon form (that is, an identity matrix followed by zero rows) for $i=1, \ldots, r-1$.
# All other blocks of ''W'' are zero (that is, $W_ = 0$ when $j \ne i, i + 1$).

In this case, we say that $W$ has Weyr structure $(n_1, n_2, \ldots , n_r)$.

Example

The following is an example of a basic Weyr matrix.

$W =$

$= \begin W_ & W_ & & \\ & W_ & W_ & \\ & & W_ & W_ \\ & & & W_ \\ \end$

In this matrix, $n=9$ and $n_1=4, n_2=2, n_3=2, n_4=1$. So $W$ has the Weyr structure $(4,2,2,1)$. Also,

$W_ = \begin \lambda & 0 & 0 & 0 \\ 0 &\lambda & 0 & 0 \\ 0 & 0 & \lambda & 0 \\ 0 & 0 & 0 & \lambda \\ \end = \lambda I_4, \quad W_ = \begin \lambda & 0 \\ 0 &\lambda & \\ \end = \lambda I_2, \quad W_ = \begin \lambda & 0 \\ 0 &\lambda & \\ \end =\lambda I_2, \quad W_ = \begin \lambda \\ \end = \lambda I_1$

and

$W_= \begin 1 & 0 \\ 0 & 1\\ 0 & 0\\ 0 & 0\\ \end, \quad W_= \begin 1 & 0 \\ 0& 1\\ \end,\quad W_ = \begin 1 \\ 0 \\ \end.$

General Weyr matrix

Definition

Let $W$ be a square matrix and let $\lambda_1, \ldots, \lambda_k$ be the distinct eigenvalues of $W$. We say that $W$ is in Weyr form (or is a Weyr matrix) if $W$ has the following form:

$W = \begin W_1 & & & \\ & W_2 & & \\ & & \ddots & \\ & & & W_k \\ \end$

where $W_i$ is a basic Weyr matrix with eigenvalue $\lambda_i$ for $i = 1, \ldots , k$.

Example

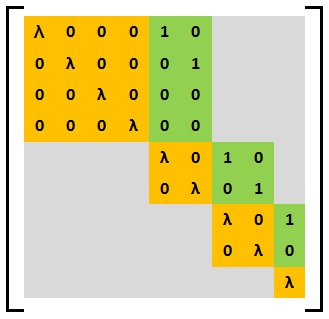
The following image shows an example of a general Weyr matrix consisting of three basic Weyr matrix blocks. The basic Weyr matrix in the top-left corner has the structure (4,2,1) with eigenvalue 4, the middle block has structure (2,2,1,1) with eigenvalue -3 and the one in the lower-right corner has the structure (3, 2) with eigenvalue 0.

Relation between Weyr and Jordan forms

The Weyr canonical form $W=P^ J P$ is related to the Jordan form $J$ by a simple permutation $P$ for each Weyr basic block as follows: The first index of each Weyr subblock forms the largest Jordan chain. After crossing out these rows and columns, the first index of each new subblock forms the second largest Jordan chain, and so forth.Sergeichuk
"Canonical matrices for linear matrix problems"
Arxiv:0709.2485 ath.RT 2007

The Weyr form is canonical

That the Weyr form is a canonical form of a matrix is a consequence of the following result: ''Each square matrix $A$ over an algebraically closed field is similar to a Weyr matrix $W$ which is unique up to permutation of its basic blocks. The matrix $W$ is called the Weyr (canonical) form of $A$.''

Computation of the Weyr canonical form

Reduction to the nilpotent case

Let $A$ be a square matrix of order $n$ over an algebraically closed field and let the distinct eigenvalues of $A$ be $\lambda_1, \lambda_2, \ldots, \lambda_k$. The Jordan–Chevalley decomposition theorem states that $A$ is similar to a block diagonal matrix of the form

$A= \begin \lambda_1I + N_1& & & \\ & \lambda_2I + N_2 & & \\ & & \ddots & \\ & & & \lambda_kI + N_k \\ \end = \begin \lambda_1I & & & \\ & \lambda_2I & & \\ & & \ddots & \\ & & & \lambda_kI \\ \end + \begin N_1& & & \\ & N_2 & & \\ & & \ddots & \\ & & & N_k \\ \end = D+N$

where $D$ is a diagonal matrix, $N$ is a nilpotent matrix, and ,N0, justifying the reduction of $N$ into subblocks $N_i$. So the problem of reducing $A$ to the Weyr form reduces to the problem of reducing the nilpotent matrices $N_i$ to the Weyr form. This is leads to the generalized eigenspace decomposition theorem.

Reduction of a nilpotent matrix to the Weyr form

Given a nilpotent square matrix $A$ of order $n$ over an algebraically closed field $F$, the following algorithm produces an invertible matrix $C$ and a Weyr matrix $W$ such that $W=C^AC$.

Step 1

Let $A_1=A$

Step 2

# Compute a basis for the null space of $A_1$.
# Extend the basis for the null space of $A_1$ to a basis for the $n$-dimensional vector space $F^n$.
# Form the matrix $P_1$ consisting of these basis vectors.
# Compute $P_1^A_1P_1=\begin0 & B_2 \\ 0 & A_2 \end$. $A_2$ is a square matrix of size $n$ − nullity $(A_1)$.

Step 3

If $A_2$ is nonzero, repeat Step 2 on $A_2$.

# Compute a basis for the null space of $A_2$.
# Extend the basis for the null space of $A_2$ to a basis for the vector space having dimension $n$ − nullity $(A_1)$.
# Form the matrix $P_2$ consisting of these basis vectors.
# Compute $P_2^A_2P_2=\begin0 & B_3 \\ 0 & A_3 \end$. $A_2$ is a square matrix of size $n$ − nullity $(A_1)$ − nullity$(A_2)$.

Step 4

Continue the processes of Steps 1 and 2 to obtain increasingly smaller square matrices $A_1, A_2, A_3, \ldots$ and associated invertible matrices $P_1, P_2, P_3, \ldots$ until the first zero matrix $A_r$ is obtained.

Step 5

The Weyr structure of $A$ is $(n_1,n_2, \ldots, n_r)$ where $n_i$ = nullity$(A_i)$.

Step 6

# Compute the matrix $P = P_1 \begin I & 0 \\ 0 & P_2 \end\begin I & 0 \\ 0 & P_3 \end\cdots \begin I & 0 \\ 0 & P_r \end$ (here the $I$'s are appropriately sized identity matrices).
# Compute $X=P^AP$. $X$ is a matrix of the following form:

:: $X = \begin0 & X_ & X_ & \cdots & X_ &X_\\ & 0 & X_ & \cdots & X_ & X_\\ & & & \ddots & \\ & & & \cdots & 0& X_ \\ & & & & & 0 \end$.

Step 7

Use elementary row operations to find an invertible matrix $Y_$ of appropriate size such that the product $Y_X_$ is a matrix of the form $I_= \begin I \\ O \end$.

Step 8

Set $Q_1=$ diag $(I,I, \ldots, Y_^, I)$ and compute $Q_1^XQ_1$. In this matrix, the $(r,r-1)$-block is $I_$.

Step 9

Find a matrix $R_1$ formed as a product of elementary matrices such that $R_1^ Q_1^XQ_1R_1$ is a matrix in which all the blocks above the block $I_$ contain only $0$'s.

Step 10

Repeat Steps 8 and 9 on column $r-1$ converting $(r-1, r-2)$-block to $I_$ via conjugation by some invertible matrix $Q_2$. Use this block to clear out the blocks above, via conjugation by a product $R_2$ of elementary matrices.

Step 11

Repeat these processes on $r-2,r-3,\ldots , 3, 2$ columns, using conjugations by $Q_3, R_3,\ldots , Q_, R_, Q_$. The resulting matrix $W$ is now in Weyr form.

Step 12

Let $C = P_1 \text (I, P_2) \cdots \text(I, P_)Q_1R_1Q_2\cdots R_Q_$. Then $W = C^AC$.

Applications of the Weyr form

Some well-known applications of the Weyr form are listed below:

# The Weyr form can be used to simplify the proof of Gerstenhaber’s Theorem which asserts that the subalgebra generated by two commuting $n \times n$ matrices has dimension at most $n$.
# A set of finite matrices is said to be approximately simultaneously diagonalizable if they can be perturbed to simultaneously diagonalizable matrices. The Weyr form is used to prove approximate simultaneous diagonalizability of various classes of matrices. The approximate simultaneous diagonalizability property has applications in the study of phylogenetic invariants in biomathematics.
# The Weyr form can be used to simplify the proofs of the irreducibility of the variety of all ''k''-tuples of commuting complex matrices.

References

{{reflist

Linear algebra
Matrix theory
Matrix normal forms
Matrix decompositions