Wave-mechanical Tunneling on:
[Wikipedia]
[Google]
[Amazon]
Quantum tunnelling, also known as tunneling ( US) is a quantum mechanical phenomenon whereby a
 The wave function of a
The wave function of a
 The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunneling.
The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunneling.
 In real life, most system are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunneling between them. This phenomenon is referred as chaos-assisted tunneling. and is characterized by sharp resonances of the tunneling rate when varying any system parameter.
In real life, most system are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunneling between them. This phenomenon is referred as chaos-assisted tunneling. and is characterized by sharp resonances of the tunneling rate when varying any system parameter.
15 PHz


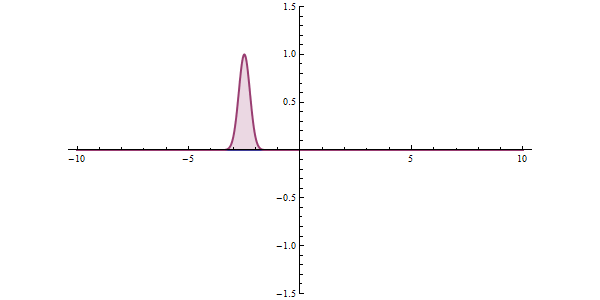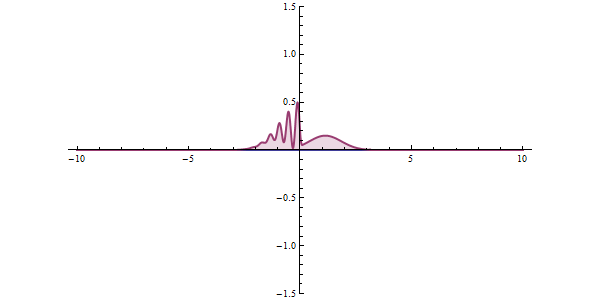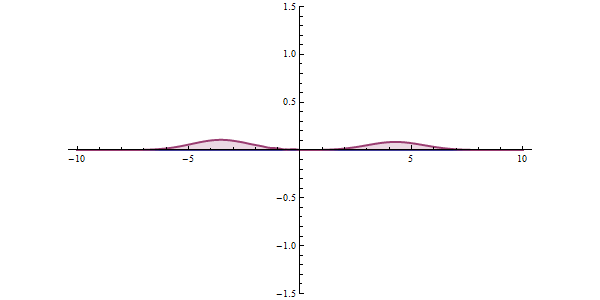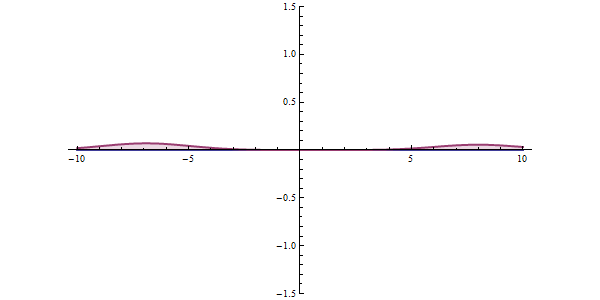 With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
Animation, applications and research linked to tunnel effect and other quantum phenomena
(Université Paris Sud)
Animated illustration of quantum tunneling in a RTD device
Interactive Solution of Schrodinger Tunnel Equation
{{Authority control Articles containing video clips Particle physics Quantum mechanics Solid state engineering
wavefunction
A wave function in quantum physics is a mathematical description of the quantum state of an isolated quantum system. The wave function is a complex-valued probability amplitude, and the probabilities for the possible results of measurements mad ...
can propagate through a potential barrier
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. ...
.
The transmission through the barrier can be finite and depends exponentially on the barrier height and barrier width. The wavefunction may disappear on one side and reappear on the other side. The wavefunction and its first derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
are continuous
Continuity or continuous may refer to:
Mathematics
* Continuity (mathematics), the opposing concept to discreteness; common examples include
** Continuous probability distribution or random variable in probability and statistics
** Continuous ...
. In steady-state, the probability flux in the forward direction is spatially uniform. No particle or wave is lost. Tunneling occurs with barriers of thickness around 1–3 nm and smaller.
Some authors also identify the mere penetration of the wavefunction into the barrier, without transmission on the other side as a tunneling effect. Quantum tunneling is not predicted by the laws of classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
where surmounting a potential barrier requires sufficient kinetic energy.
Quantum tunneling plays an essential role in physical phenomena such as nuclear fusion and alpha radioactive decay of atomic nuclei. It has applications in the tunnel diode
A tunnel diode or Esaki diode is a type of semiconductor diode that has effectively "negative resistance" due to the quantum mechanical effect called tunneling. It was invented in August 1957 by Leo Esaki, Yuriko Kurose, and Takashi Suzuki ...
, quantum computing
Quantum computing is a type of computation whose operations can harness the phenomena of quantum mechanics, such as superposition, interference, and entanglement. Devices that perform quantum computations are known as quantum computers. Though ...
, and in the scanning tunneling microscope.
The effect was predicted in the early 20th century. Its acceptance as a general physical phenomenon came mid-century.
Quantum tunneling limits the minimum size of devices used in microelectronics
Microelectronics is a subfield of electronics. As the name suggests, microelectronics relates to the study and manufacture (or microfabrication) of very small electronic designs and components. Usually, but not always, this means micrometre-sc ...
because electrons tunnel readily through insulating layers and transistor
upright=1.4, gate (G), body (B), source (S) and drain (D) terminals. The gate is separated from the body by an insulating layer (pink).
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch e ...
s that are thinner than about 1 nm.
Tunneling is best explained in terms of solutions of the Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the ...
, as described in 2.1 (below).
History
Quantum tunneling was developed from the study of radioactivity, which was discovered in 1896 by Henri Becquerel. Radioactivity was examined further byMarie Curie
Marie Salomea Skłodowska–Curie ( , , ; born Maria Salomea Skłodowska, ; 7 November 1867 – 4 July 1934) was a Polish and naturalized-French physicist and chemist who conducted pioneering research on radioactivity. She was the first ...
and Pierre Curie
Pierre Curie ( , ; 15 May 1859 – 19 April 1906) was a French physicist, a pioneer in crystallography, magnetism, piezoelectricity, and radioactivity. In 1903, he received the Nobel Prize in Physics with his wife, Marie Curie, and Henri Becqu ...
, for which they earned the Nobel Prize in Physics
)
, image = Nobel Prize.png
, alt = A golden medallion with an embossed image of a bearded man facing left in profile. To the left of the man is the text "ALFR•" then "NOBEL", and on the right, the text (smaller) "NAT•" then " ...
in 1903. Ernest Rutherford and Egon Schweidler
Egon Schweidler, (* 10 February 1873, in Vienna; † 10 February 1948, in Salzburg Seeham) was an Austrian physicist.
Biography
He was born in 1873 as the son of the court and ''Gerichtsadvokaten'' Emil von Schweidler born in Vienna. After studyin ...
studied its nature, which was later verified empirically by Friedrich Kohlrausch. The idea of half-life
Half-life (symbol ) is the time required for a quantity (of substance) to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable ato ...
and the possibility of predicting decay was created from their work.
In 1901, Robert Francis Earhart
The name Robert is an ancient Germanic given name, from Proto-Germanic "fame" and "bright" (''Hrōþiberhtaz''). Compare Old Dutch ''Robrecht'' and Old High German ''Hrodebert'' (a compound of '' Hruod'' ( non, Hróðr) "fame, glory, honou ...
discovered an unexpected conduction regime while investigating the conduction of gases between closely spaced electrodes using the Michelson interferometer. J. J. Thomson
Sir Joseph John Thomson (18 December 1856 – 30 August 1940) was a British physicist and Nobel Laureate in Physics, credited with the discovery of the electron, the first subatomic particle to be discovered.
In 1897, Thomson showed that c ...
commented that the finding warranted further investigation. In 1911 and then 1914, then-graduate student Franz Rother directly measured steady field emission currents. He employed Earhart's method for controlling and measuring the electrode separation, but with a sensitive platform galvanometer. In 1926, Rother measured the field emission current
Field electron emission, also known as field emission (FE) and electron field emission, is emission of electrons induced by an electrostatic field. The most common context is field emission from a solid surface into a vacuum. However, field emissio ...
s in a "hard" vacuum between closely spaced electrodes.
Quantum tunneling was first noticed in 1927 by Friedrich Hund while he was calculating the ground state of the double-well potential The so-called double-well potential is one of a number of Quartic function, quartic potentials of considerable interest in quantum mechanics, in quantum field theory and elsewhere for the exploration of various physical phenomena or mathematical pro ...
. Leonid Mandelstam
Leonid Isaakovich Mandelstam or Mandelshtam ( be, Леанід Ісаакавіч Мандэльштам; rus, Леонид Исаакович Мандельштам, p=lʲɪɐˈnʲit ɨsɐˈakəvʲɪtɕ mənʲdʲɪlʲˈʂtam, a=Ru-Leonid_Mande ...
and Mikhail Leontovich
Mikhail Alexandrovich Leontovich (russian: Михаи́л Алекса́ндрович Леонто́вич, 22 February 1903, St. Petersburg – 30 March 1981, Moscow) was a Soviet physicist, member of USSR Academy of Sciences, specializing in pl ...
discovered it independently in the same year. They were analyzing the implications of the then new Schrödinger wave equation.
Its first application was a mathematical explanation for alpha decay
Alpha decay or α-decay is a type of radioactive decay in which an atomic nucleus emits an alpha particle (helium nucleus) and thereby transforms or 'decays' into a different atomic nucleus, with a mass number that is reduced by four and an atom ...
, which was developed in 1928 by George Gamow
George Gamow (March 4, 1904 – August 19, 1968), born Georgiy Antonovich Gamov ( uk, Георгій Антонович Гамов, russian: Георгий Антонович Гамов), was a Russian-born Soviet and American polymath, theoreti ...
(who was aware of Mandelstam and Leontovich's findings) and independently by Ronald Gurney and Edward Condon. The latter researchers simultaneously solved the Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the ...
for a model nuclear potential and derived a relationship between the half-life
Half-life (symbol ) is the time required for a quantity (of substance) to reduce to half of its initial value. The term is commonly used in nuclear physics to describe how quickly unstable atoms undergo radioactive decay or how long stable ato ...
of the particle and the energy of emission that depended directly on the mathematical probability of tunneling.
After attending a Gamow seminar, Max Born
Max Born (; 11 December 1882 – 5 January 1970) was a German physicist and mathematician who was instrumental in the development of quantum mechanics. He also made contributions to solid-state physics and optics and supervised the work of a n ...
recognised the generality of tunneling. He realised that it was not restricted to nuclear physics
Nuclear physics is the field of physics that studies atomic nuclei and their constituents and interactions, in addition to the study of other forms of nuclear matter.
Nuclear physics should not be confused with atomic physics, which studies the ...
, but was a general result of quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
that applied to many different systems. Shortly thereafter, both groups considered the case of particles tunneling into the nucleus. The study of semiconductor
A semiconductor is a material which has an electrical resistivity and conductivity, electrical conductivity value falling between that of a electrical conductor, conductor, such as copper, and an insulator (electricity), insulator, such as glas ...
s and the development of transistor
upright=1.4, gate (G), body (B), source (S) and drain (D) terminals. The gate is separated from the body by an insulating layer (pink).
A transistor is a semiconductor device used to Electronic amplifier, amplify or electronic switch, switch e ...
s and diode
A diode is a two-terminal electronic component that conducts current primarily in one direction (asymmetric conductance); it has low (ideally zero) resistance in one direction, and high (ideally infinite) resistance in the other.
A diode ...
s led to the acceptance of electron tunneling in solids by 1957. Leo Esaki
Reona Esaki (江崎 玲於奈 ''Esaki Reona'', born March 12, 1925), also known as Leo Esaki, is a Japanese physicist who shared the Nobel Prize in Physics in 1973 with Ivar Giaever and Brian David Josephson for his work in electron tunneling in ...
, Ivar Giaever
Ivar Giaever ( no, Giæver, ; born April 5, 1929) is a Norwegian-American engineer and physicist who shared the Nobel Prize in Physics in 1973 with Leo Esaki and Brian Josephson "for their discoveries regarding tunnelling phenomena in solids". Gi ...
and Brian Josephson predicted the tunneling of superconducting Cooper pairs, for which they received the Nobel Prize in Physics
)
, image = Nobel Prize.png
, alt = A golden medallion with an embossed image of a bearded man facing left in profile. To the left of the man is the text "ALFR•" then "NOBEL", and on the right, the text (smaller) "NAT•" then " ...
in 1973. In 2016, the quantum tunneling of water
The quantum tunneling of water occurs when water molecules in nanochannels exhibit quantum tunneling behavior that smears out the positions of the hydrogen atoms into a pair of correlated rings. In that state, the water molecules become deloca ...
was discovered.
Introduction to the concept
Quantum tunneling falls under the domain ofquantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
: the study of what happens at the quantum scale. Tunneling cannot be directly perceived. Much of its understanding is shaped by the microscopic world, which classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
cannot explain. To understand the phenomenon
A phenomenon ( : phenomena) is an observable event. The term came into its modern philosophical usage through Immanuel Kant, who contrasted it with the noumenon, which ''cannot'' be directly observed. Kant was heavily influenced by Gottfried W ...
, particles attempting to travel across a potential barrier
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. ...
can be compared to a ball trying to roll over a hill.
Quantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
and classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
differ in their treatment of this scenario. Classical mechanics predicts that particles that do not have enough energy to classically surmount a barrier cannot reach the other side. Thus, a ball without sufficient energy to surmount the hill would roll back down. A ball that lacks the energy to penetrate a wall bounces back. Alternatively, the ball might become part of the wall (absorption).
In quantum mechanics, these particles can, with a small probability, ''tunnel'' to the other side, thus crossing the barrier. The ball, in a sense, ''borrows'' energy from its surroundings to cross the wall. It then repays the energy by making the reflected electrons more energetic than they otherwise would have been.
The reason for this difference comes from treating matter as having properties of waves and particles. One interpretation of this duality involves the Heisenberg uncertainty principle
In quantum mechanics, the uncertainty principle (also known as Heisenberg's uncertainty principle) is any of a variety of mathematical inequalities asserting a fundamental limit to the accuracy with which the values for certain pairs of physic ...
, which defines a limit on how precisely the position and the momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass an ...
of a particle can be simultaneously known. This implies that no solutions have a probability of exactly zero (or one), though it may approach infinity. If, for example, the calculation for its position was taken as a probability of 1, its speed would have to be infinity (an impossibility). Hence, the probability of a given particle's existence on the opposite side of an intervening barrier is non-zero, and such particles will appear on the 'other' (a semantically difficult word in this instance) side in proportion to this probability.
The tunneling problem
 The wave function of a
The wave function of a physical system
A physical system is a collection of physical objects.
In physics, it is a portion of the physical universe chosen for analysis. Everything outside the system is known as the environment. The environment is ignored except for its effects on the ...
of particles specifies everything that can be known about the system. Therefore, problems in quantum mechanics analyze the system's wave function. Using mathematical formulations, such as the Schrödinger equation
The Schrödinger equation is a linear partial differential equation that governs the wave function of a quantum-mechanical system. It is a key result in quantum mechanics, and its discovery was a significant landmark in the development of the ...
, the time evolution of a known wave function can be deduced. The square of the absolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), an ...
of this wavefunction is directly related to the probability distribution of the particle positions, which describes the probability that the particles are at any given places.
In both illustrations, as as single-particle wave packet impinges on the barrier, most of it is reflected and some is transmitted through the barrier. The wave packet becomes more de-localized: it is now on both sides of the barrier and lower in maximum amplitude, but equal in integrated square-magnitude, meaning that the particle is somewhere remains unity. The wider the barrier and the higher the barrier energy, the lower the probability of tunneling.
Some models of a tunneling barrier, such as the rectangular barriers shown, can be analysed and solved algebraically. Most problems do not have an algebraic solution, so numerical solutions are used. " Semiclassical methods" offer approximate solutions that are easier to compute, such as the WKB approximation.
Dynamical tunneling
 The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunneling.
The concept of quantum tunneling can be extended to situations where there exists a quantum transport between regions that are classically not connected even if there is no associated potential barrier. This phenomenon is known as dynamical tunneling.
Tunneling in phase space
The concept of dynamical tunneling is particularly suited to address the problem of quantum tunneling in high dimensions (d>1). In the case of anintegrable system
In mathematics, integrability is a property of certain dynamical systems. While there are several distinct formal definitions, informally speaking, an integrable system is a dynamical system with sufficiently many conserved quantities, or first ...
, where bounded classical trajectories are confined onto tori in phase space
In dynamical system theory, a phase space is a space in which all possible states of a system are represented, with each possible state corresponding to one unique point in the phase space. For mechanical systems, the phase space usually ...
, tunneling can be understood as the quantum transport between semi-classical states built on two distinct but symmetric tori.
Chaos-assisted tunneling
 In real life, most system are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunneling between them. This phenomenon is referred as chaos-assisted tunneling. and is characterized by sharp resonances of the tunneling rate when varying any system parameter.
In real life, most system are not integrable and display various degrees of chaos. Classical dynamics is then said to be mixed and the system phase space is typically composed of islands of regular orbits surrounded by a large sea of chaotic orbits. The existence of the chaotic sea, where transport is classically allowed, between the two symmetric tori then assists the quantum tunneling between them. This phenomenon is referred as chaos-assisted tunneling. and is characterized by sharp resonances of the tunneling rate when varying any system parameter.
Resonance-assisted tunneling
When is small in front of the size of the regular islands, the fine structure of the classical phase space plays a key role in tunneling. In particular the two symmetric tori are coupled "via a succession of classically forbidden transitions across nonlinear resonances" surrounding the two islands.Related phenomena
Several phenomena have the same behavior as quantum tunneling, and can be accurately described by tunneling. Examples include the tunneling of a classical wave-particle association,evanescent wave coupling
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source (oscillati ...
(the application of Maxwell's wave-equation to light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 tera ...
) and the application of the non-dispersive wave-equation from acoustics
Acoustics is a branch of physics that deals with the study of mechanical waves in gases, liquids, and solids including topics such as vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician ...
applied to "waves on strings". Evanescent wave coupling, until recently, was only called "tunneling" in quantum mechanics; now it is used in other contexts.
These effects are modeled similarly to the rectangular potential barrier
In quantum mechanics, the rectangular (or, at times, square) potential barrier is a standard one-dimensional problem that demonstrates the phenomena of wave-mechanical tunneling (also called "quantum tunneling") and wave-mechanical reflection. ...
. In these cases, one transmission medium
A transmission medium is a system or substance that can mediate the propagation of signals for the purposes of telecommunication. Signals are typically imposed on a wave of some kind suitable for the chosen medium. For example, data can modulate ...
through which the wave propagates that is the same or nearly the same throughout, and a second medium through which the wave travels differently. This can be described as a thin region of medium B between two regions of medium A. The analysis of a rectangular barrier by means of the Schrödinger equation can be adapted to these other effects provided that the wave equation has travelling wave solutions in medium A but real exponential solutions in medium B.
In optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviole ...
, medium A is a vacuum while medium B is glass. In acoustics, medium A may be a liquid or gas and medium B a solid. For both cases, medium A is a region of space where the particle's total energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of heat an ...
is greater than its potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
and medium B is the potential barrier. These have an incoming wave and resultant waves in both directions. There can be more mediums and barriers, and the barriers need not be discrete. Approximations are useful in this case.
Applications
Tunneling is the cause of some important macroscopic physical phenomena. Quantum tunnelling has important implications on functioning ofnanotechnology
Nanotechnology, also shortened to nanotech, is the use of matter on an atomic, molecular, and supramolecular scale for industrial purposes. The earliest, widespread description of nanotechnology referred to the particular technological goal o ...
.
Electronics
Tunneling is a source of current leakage invery-large-scale integration
Very large-scale integration (VLSI) is the process of creating an integrated circuit (IC) by combining millions or billions of MOS transistors onto a single chip. VLSI began in the 1970s when MOS integrated circuit (Metal Oxide Semiconductor) c ...
(VLSI) electronics and results in the substantial power drain and heating effects that plague such devices. It is considered the lower limit on how microelectronic device elements can be made. Tunneling is a fundamental technique used to program the floating gates of flash memory
Flash memory is an electronic non-volatile computer memory storage medium that can be electrically erased and reprogrammed. The two main types of flash memory, NOR flash and NAND flash, are named for the NOR and NAND logic gates. Both us ...
.
Cold emission
Cold emission ofelectrons
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
is relevant to semiconductor
A semiconductor is a material which has an electrical resistivity and conductivity, electrical conductivity value falling between that of a electrical conductor, conductor, such as copper, and an insulator (electricity), insulator, such as glas ...
s and superconductor physics. It is similar to thermionic emission, where electrons randomly jump from the surface of a metal to follow a voltage bias because they statistically end up with more energy than the barrier, through random collisions with other particles. When the electric field is very large, the barrier becomes thin enough for electrons to tunnel out of the atomic state, leading to a current that varies approximately exponentially with the electric field. These materials are important for flash memory
Flash memory is an electronic non-volatile computer memory storage medium that can be electrically erased and reprogrammed. The two main types of flash memory, NOR flash and NAND flash, are named for the NOR and NAND logic gates. Both us ...
, vacuum tubes, as well as some electron microscopes.
Tunnel junction
A simple barrier can be created by separating two conductors with a very thin insulator. These are tunnel junctions, the study of which requires understanding quantum tunneling. Josephson junctions take advantage of quantum tunneling and superconductivity to create the Josephson effect. This has applications in precision measurements of voltages and magnetic fields, as well as the multijunction solar cell.Quantum-dot cellular automata
QCA is a molecular binary logic synthesis technology that operates by the inter-island electron tunneling system. This is a very low power and fast device that can operate at a maximum frequency o15 PHz
Tunnel diode

Diode
A diode is a two-terminal electronic component that conducts current primarily in one direction (asymmetric conductance); it has low (ideally zero) resistance in one direction, and high (ideally infinite) resistance in the other.
A diode ...
s are electrical semiconductor device
A semiconductor device is an electronic component that relies on the electronic properties of a semiconductor material (primarily silicon, germanium, and gallium arsenide, as well as organic semiconductors) for its function. Its conductivity li ...
s that allow electric current
An electric current is a stream of charged particles, such as electrons or ions, moving through an electrical conductor or space. It is measured as the net rate of flow of electric charge through a surface or into a control volume. The moving pa ...
flow in one direction more than the other. The device depends on a depletion layer
In semiconductor physics, the depletion region, also called depletion layer, depletion zone, junction region, space charge region or space charge layer, is an insulating region within a conductive, doped semiconductor material where the mobile ...
between N-type and P-type semiconductor
An extrinsic semiconductor is one that has been '' doped''; during manufacture of the semiconductor crystal a trace element or chemical called a doping agent has been incorporated chemically into the crystal, for the purpose of giving it different ...
s to serve its purpose. When these are heavily doped the depletion layer can be thin enough for tunneling. When a small forward bias is applied, the current due to tunneling is significant. This has a maximum at the point where the voltage bias
In electronics, biasing is the setting of DC (direct current) operating conditions (current and voltage) of an active device in an amplifier. Many electronic devices, such as diodes, transistors and vacuum tubes, whose function is processing ...
is such that the energy level of the p and n conduction band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in w ...
s are the same. As the voltage bias is increased, the two conduction bands no longer line up and the diode acts typically.
Because the tunneling current drops off rapidly, tunnel diodes can be created that have a range of voltages for which current decreases as voltage increases. This peculiar property is used in some applications, such as high speed devices where the characteristic tunneling probability changes as rapidly as the bias voltage.
The resonant tunneling diode
A resonant-tunneling diode (RTD) is a diode with a resonant-tunneling structure in which electrons can tunnel through some resonant states at certain energy levels. The current–voltage characteristic often exhibits negative differential resistan ...
makes use of quantum tunneling in a very different manner to achieve a similar result. This diode has a resonant voltage for which a lot of current favors a particular voltage, achieved by placing two thin layers with a high energy conductance band near each other. This creates a quantum potential well
A potential well is the region surrounding a local minimum of potential energy. Energy captured in a potential well is unable to convert to another type of energy (kinetic energy in the case of a gravitational potential well) because it is captur ...
that has a discrete lowest energy level. When this energy level is higher than that of the electrons, no tunneling occurs and the diode is in reverse bias. Once the two voltage energies align, the electrons flow like an open wire. As the voltage further increases, tunneling becomes improbable and the diode acts like a normal diode again before a second energy level becomes noticeable.
Tunnel field-effect transistors
A European research project demonstratedfield effect transistors
The field-effect transistor (FET) is a type of transistor that uses an electric field to control the flow of current in a semiconductor. FETs (JFETs or MOSFETs) are devices with three terminals: ''source'', ''gate'', and ''drain''. FETs control ...
in which the gate (channel) is controlled via quantum tunneling rather than by thermal injection, reducing gate voltage from ≈1 volt to 0.2 volts and reducing power consumption by up to 100×. If these transistors can be scaled up into VLSI chips, they would improve the performance per power of integrated circuit
An integrated circuit or monolithic integrated circuit (also referred to as an IC, a chip, or a microchip) is a set of electronic circuits on one small flat piece (or "chip") of semiconductor material, usually silicon. Large numbers of tiny ...
s.
Nuclear fusion
Quantum tunneling is an essential phenomenon for nuclear fusion. The temperature in stellar cores is generally insufficient to allow atomic nuclei to overcome the Coulomb barrier and achievethermonuclear fusion
Thermonuclear fusion is the process of atomic nuclei combining or “fusing” using high temperatures to drive them close enough together for this to become possible. There are two forms of thermonuclear fusion: ''uncontrolled'', in which the re ...
. Quantum tunneling increases the probability of penetrating this barrier. Though this probability is still low, the extremely large number of nuclei in the core of a star is sufficient to sustain a steady fusion reaction.
Radioactive decay
Radioactive decay is the process of emission of particles and energy from the unstable nucleus of an atom to form a stable product. This is done via the tunneling of a particle out of the nucleus (an electron tunneling into the nucleus iselectron capture
Electron capture (K-electron capture, also K-capture, or L-electron capture, L-capture) is a process in which the proton-rich nucleus of an electrically neutral atom absorbs an inner atomic electron, usually from the K or L electron shells. Thi ...
). This was the first application of quantum tunneling. Radioactive decay is a relevant issue for astrobiology
Astrobiology, and the related field of exobiology, is an interdisciplinary scientific field that studies the origins, early evolution, distribution, and future of life in the universe. Astrobiology is the multidisciplinary field that investig ...
as this consequence of quantum tunneling creates a constant energy source over a large time interval for environments outside the circumstellar habitable zone where insolation would not be possible ( subsurface oceans) or effective.
Quantum tunnelling may be one of the mechanisms of hypothetical proton decay.ucl-th/9809006Time-dependent properties of proton decay from crossing single-particle metastable states in deformed nuclei">
Astrochemistry in interstellar clouds
By including quantum tunneling, the astrochemical syntheses of various molecules ininterstellar cloud
An interstellar cloud is generally an accumulation of gas, plasma, and dust in our and other galaxies. Put differently, an interstellar cloud is a denser-than-average region of the interstellar medium, the matter and radiation that exists in t ...
s can be explained, such as the synthesis of molecular hydrogen, water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as a ...
(ice
Ice is water frozen into a solid state, typically forming at or below temperatures of 0 degrees Celsius or Depending on the presence of impurities such as particles of soil or bubbles of air, it can appear transparent or a more or less opaq ...
) and the prebiotic important formaldehyde
Formaldehyde ( , ) (systematic name methanal) is a naturally occurring organic compound with the formula and structure . The pure compound is a pungent, colourless gas that polymerises spontaneously into paraformaldehyde (refer to section F ...
.
Quantum biology
Quantum tunneling is among the central non-trivial quantum effects inquantum biology
Quantum biology is the study of applications of quantum mechanics and theoretical chemistry to aspects of biology that cannot be accurately described by the classical laws of physics. An understanding of fundamental quantum interactions is importan ...
. Here it is important both as electron tunneling and proton tunneling
A proton is a stable subatomic particle, symbol , H+, or 1H+ with a positive electric charge of +1 ''e'' elementary charge. Its mass is slightly less than that of a neutron and 1,836 times the mass of an electron (the proton–electron mas ...
. Electron tunneling is a key factor in many biochemical redox reactions
Redox (reduction–oxidation, , ) is a type of chemical reaction in which the oxidation states of substrate change. Oxidation is the loss of electrons or an increase in the oxidation state, while reduction is the gain of electrons or a d ...
(photosynthesis
Photosynthesis is a process used by plants and other organisms to convert light energy into chemical energy that, through cellular respiration, can later be released to fuel the organism's activities. Some of this chemical energy is stored i ...
, cellular respiration
Cellular respiration is the process by which biological fuels are oxidised in the presence of an inorganic electron acceptor such as oxygen to produce large amounts of energy, to drive the bulk production of ATP. Cellular respiration may be des ...
) as well as enzymatic catalysis. Proton tunneling is a key factor in spontaneous DNA mutation.
Spontaneous mutation occurs when normal DNA replication takes place after a particularly significant proton has tunnelled. A hydrogen bond joins DNA base pairs. A double well potential along a hydrogen bond separates a potential energy barrier. It is believed that the double well potential is asymmetric, with one well deeper than the other such that the proton normally rests in the deeper well. For a mutation to occur, the proton must have tunnelled into the shallower well. The proton's movement from its regular position is called a tautomeric transition. If DNA replication takes place in this state, the base pairing rule for DNA may be jeopardised, causing a mutation. Per-Olov Lowdin was the first to develop this theory of spontaneous mutation within the double helix. Other instances of quantum tunneling-induced mutations in biology are believed to be a cause of ageing and cancer.
Quantum conductivity
While theDrude-Lorentz model
The Drude model of electrical conduction was proposed in 1900 by Paul Drude to explain the transport properties of electrons in materials (especially metals). Basically, Ohm's law was well established and stated that the current ''J'' and voltag ...
of electrical conductivity
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allow ...
makes excellent predictions about the nature of electrons conducting in metals, it can be furthered by using quantum tunneling to explain the nature of the electron's collisions. When a free electron wave packet encounters a long array of uniformly spaced barriers, the reflected part of the wave packet interferes uniformly with the transmitted one between all barriers so that 100% transmission becomes possible. The theory predicts that if positively charged nuclei form a perfectly rectangular array, electrons will tunnel through the metal as free electrons, leading to extremely high conductance, and that impurities in the metal will disrupt it significantly.
Scanning tunneling microscope
The scanning tunneling microscope (STM), invented byGerd Binnig
Gerd Binnig (; born 20 July 1947) is a German physicist. He is most famous for having won the Nobel Prize in Physics jointly with Heinrich Rohrer in 1986 for the invention of the scanning tunneling microscope.
Early life and education
Binnig wa ...
and Heinrich Rohrer
Heinrich Rohrer (6 June 1933 – 16 May 2013) was a Swiss physicist who shared half of the 1986 Nobel Prize in Physics with Gerd Binnig for the design of the scanning tunneling microscope (STM). The other half of the Prize was awarded to Ernst R ...
, may allow imaging of individual atoms on the surface of a material. It operates by taking advantage of the relationship between quantum tunneling with distance. When the tip of the STM's needle is brought close to a conduction surface that has a voltage bias, measuring the current of electrons that are tunneling between the needle and the surface reveals the distance between the needle and the surface. By using piezoelectric rods that change in size when voltage is applied, the height of the tip can be adjusted to keep the tunneling current constant. The time-varying voltages that are applied to these rods can be recorded and used to image the surface of the conductor. STMs are accurate to 0.001 nm, or about 1% of atomic diameter.
Kinetic isotope effect
Inchemical kinetics
Chemical kinetics, also known as reaction kinetics, is the branch of physical chemistry that is concerned with understanding the rates of chemical reactions. It is to be contrasted with chemical thermodynamics, which deals with the direction in wh ...
, the substitution of a light isotope
Isotopes are two or more types of atoms that have the same atomic number (number of protons in their nuclei) and position in the periodic table (and hence belong to the same chemical element), and that differ in nucleon numbers (mass numbers) ...
of an element with a heavier one typically results in a slower reaction rate. This is generally attributed to differences in the zero-point vibrational energies for chemical bonds containing the lighter and heavier isotopes and is generally modeled using transition state theory. However, in certain cases, large isotope effects are observed that cannot be accounted for by a semi-classical treatment, and quantum tunneling is required. R. P. Bell developed a modified treatment of Arrhenius kinetics that is commonly used to model this phenomenon.
Faster than light
Some physicists have claimed that it is possible for spin-zero particles to travel faster than thespeed of light
The speed of light in vacuum, commonly denoted , is a universal physical constant that is important in many areas of physics. The speed of light is exactly equal to ). According to the special theory of relativity, is the upper limit ...
when tunneling. This appears to violate the principle of causality
Causality (also referred to as causation, or cause and effect) is influence by which one event, process, state, or object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the cau ...
, since a frame of reference
In physics and astronomy, a frame of reference (or reference frame) is an abstract coordinate system whose origin, orientation, and scale are specified by a set of reference points― geometric points whose position is identified both mathema ...
then exists in which the particle arrives before it has left. In 1998, Francis E. Low
Francis Eugene Low (October 27, 1921 – February 16, 2007) was an American theoretical physicist. He was an Institute Professor at MIT, and served as provost there from 1980 to 1985.
He was a member of the influential JASON Defense Advisory Gro ...
reviewed briefly the phenomenon of zero-time tunneling. More recently, experimental tunneling time data of phonons, photons
A photon () is an elementary particle that is a quantum of the electromagnetic field, including electromagnetic radiation such as light and radio waves, and the force carrier for the electromagnetic force. Photons are massless, so they alway ...
, and electrons
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
was published by Günter Nimtz
Günter Nimtz (born 22 September 1936) is a German physicist, working at the 2nd Physics Institute at the University of Cologne in Germany. He has investigated narrow-gap semiconductors and liquid crystals. His claims show that particles may tra ...
.
Other physicists, such as Herbert Winful
Herbert Graves Winful (born 3 December 1952) is a Ghanaian-American engineering professor, whose numerous honours include in 2020 the Quantum Electronics Award. He is the Joseph E. and Anne P. Rowe Professor of Electrical Engineering, Arthur F. ...
, disputed these claims. Winful argued that the wavepacket of a tunneling particle propagates locally, so a particle can't tunnel through the barrier non-locally. Winful also argued that the experiments that are purported to show non-local propagation have been misinterpreted. In particular, the group velocity of a wavepacket does not measure its speed, but is related to the amount of time the wavepacket is stored in the barrier. But the problem remains that the wave function still rises inside the barrier at all points at the same time. In other words, in any region that is inaccessible to measurement, non-local propagation is still mathematically certain.
An experiment done in 2020, overseen by Aephraim Steinberg, showed that particles should be able to tunnel at apparent speeds faster than light.
Mathematical discussion

The Schrödinger equation
The time-independent Schrödinger equation for one particle in onedimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), lin ...
can be written as
or
where
* is the reduced Planck's constant,
* ''m'' is the particle mass,
* ''x'' represents distance measured in the direction of motion of the particle,
* Ψ is the Schrödinger wave function,
* ''V'' is the potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
of the particle (measured relative to any convenient reference level),
* ''E'' is the energy of the particle that is associated with motion in the ''x''-axis (measured relative to ''V''),
* ''M''(''x'') is a quantity defined by ''V''(''x'') − ''E'' which has no accepted name in physics.
The solutions of the Schrödinger equation take different forms for different values of ''x'', depending on whether ''M''(''x'') is positive or negative. When ''M''(''x'') is constant and negative, then the Schrödinger equation can be written in the form
:
The solutions of this equation represent travelling waves, with phase-constant +''k'' or -''k''. Alternatively, if ''M''(''x'') is constant and positive, then the Schrödinger equation can be written in the form
:
The solutions of this equation are rising and falling exponentials in the form of evanescent wave
In electromagnetics, an evanescent field, or evanescent wave, is an oscillating electric and/or magnetic field that does not propagate as an electromagnetic wave but whose energy is spatially concentrated in the vicinity of the source (oscillati ...
s. When ''M''(''x'') varies with position, the same difference in behaviour occurs, depending on whether M(x) is negative or positive. It follows that the sign of ''M''(''x'') determines the nature of the medium, with negative M(x) corresponding to medium A and positive ''M''(''x'') corresponding to medium B. It thus follows that evanescent wave coupling can occur if a region of positive ''M''(''x'') is sandwiched between two regions of negative ''M''(''x''), hence creating a potential barrier.
The mathematics of dealing with the situation where ''M''(''x'') varies with ''x'' is difficult, except in special cases that usually do not correspond to physical reality. A full mathematical treatment appears in the 1965 monograph by Fröman and Fröman. Their ideas have not been incorporated into physics textbooks, but their corrections have little quantitative effect.
The WKB approximation
The wave function is expressed as the exponential of a function: where is then separated into real and imaginary parts: where ''A''(''x'') and ''B''(''x'') are real-valued functions. Substituting the second equation into the first and using the fact that the imaginary part needs to be 0 results in: To solve this equation using the semiclassical approximation, each function must be expanded as apower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a const ...
in . From the equations, the power series must start with at least an order of to satisfy the real part of the equation; for a good classical limit starting with the highest power of Planck's constant possible is preferable, which leads to
and
with the following constraints on the lowest order terms,
and
At this point two extreme cases can be considered.
Case 1
If the amplitude varies slowly as compared to the phase and
which corresponds to classical motion. Resolving the next order of expansion yields
Case 2
If the phase varies slowly as compared to the amplitude, and
which corresponds to tunneling. Resolving the next order of the expansion yields
In both cases it is apparent from the denominator that both these approximate solutions are bad near the classical turning points . Away from the potential hill, the particle acts similar to a free and oscillating wave; beneath the potential hill, the particle undergoes exponential changes in amplitude. By considering the behaviour at these limits and classical turning points a global solution can be made.
To start, a classical turning point, is chosen and is expanded in a power series about :
Keeping only the first order term ensures linearity:
Using this approximation, the equation near becomes a differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
:
This can be solved using Airy functions as solutions.
Taking these solutions for all classical turning points, a global solution can be formed that links the limiting solutions. Given the two coefficients on one side of a classical turning point, the two coefficients on the other side of a classical turning point can be determined by using this local solution to connect them.
Hence, the Airy function solutions will asymptote into sine, cosine and exponential functions in the proper limits. The relationships between and are
and
: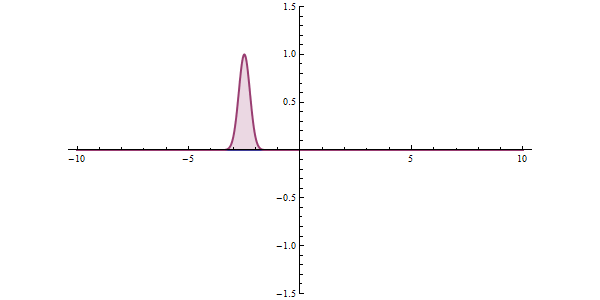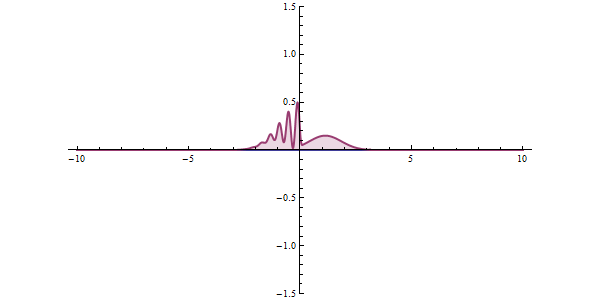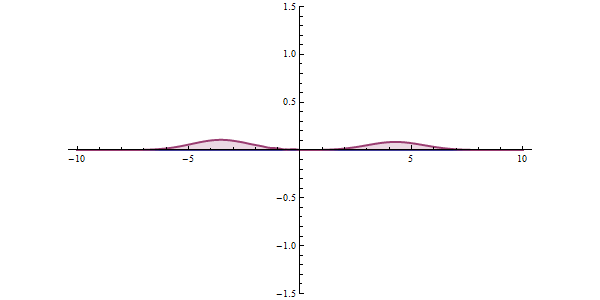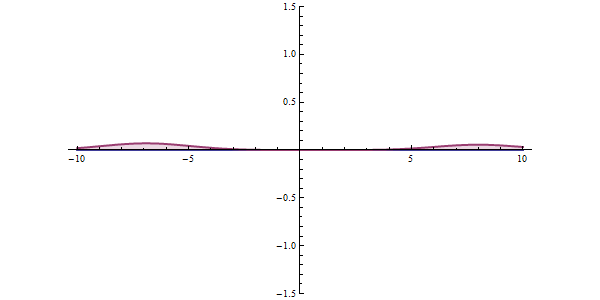 With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
With the coefficients found, the global solution can be found. Therefore, the transmission coefficient for a particle tunneling through a single potential barrier is
where are the two classical turning points for the potential barrier.
For a rectangular barrier, this expression simplifies to:
See also
*Dielectric barrier discharge
Dielectric-barrier discharge (DBD) is the electrical discharge between two electrodes separated by an insulating dielectric barrier. Originally called silent (inaudible) discharge and also known as ozone production discharge or partial dischar ...
* Field electron emission
Field electron emission, also known as field emission (FE) and electron field emission, is emission of electrons induced by an electrostatic field. The most common context is field emission from a solid surface into a vacuum. However, field emissio ...
* Holstein–Herring method The Holstein– Herring method, also called the surface Integral method, or Smirnov's method is an effective means of getting the exchange energy splittings of asymptotically degenerate energy states in molecular systems. Although the exchange energ ...
* Proton tunneling
A proton is a stable subatomic particle, symbol , H+, or 1H+ with a positive electric charge of +1 ''e'' elementary charge. Its mass is slightly less than that of a neutron and 1,836 times the mass of an electron (the proton–electron mas ...
* Quantum cloning
Quantum cloning is a process that takes an arbitrary, unknown quantum state and makes an exact copy without altering the original state in any way. Quantum cloning is forbidden by the laws of quantum mechanics as shown by the no cloning theorem, wh ...
* Superconducting tunnel junction
* Tunnel diode
A tunnel diode or Esaki diode is a type of semiconductor diode that has effectively "negative resistance" due to the quantum mechanical effect called tunneling. It was invented in August 1957 by Leo Esaki, Yuriko Kurose, and Takashi Suzuki ...
* Tunnel junction
In electronics/spintronics, a tunnel junction is a barrier, such as a thin insulating layer or electric potential, between two electrically conducting materials. Electrons (or quasiparticles) pass through the barrier by the process of quantum tunn ...
* White hole
In general relativity, a white hole is a hypothetical region of spacetime and singularity that cannot be entered from the outside, although energy-matter, light and information can escape from it. In this sense, it is the reverse of a black ho ...
References
Further reading
* * * * * * *External links
Animation, applications and research linked to tunnel effect and other quantum phenomena
(Université Paris Sud)
Animated illustration of quantum tunneling in a RTD device
Interactive Solution of Schrodinger Tunnel Equation
{{Authority control Articles containing video clips Particle physics Quantum mechanics Solid state engineering