Uniform 6-honeycomb on:
[Wikipedia]
[Google]
[Amazon]
In seven-dimensional
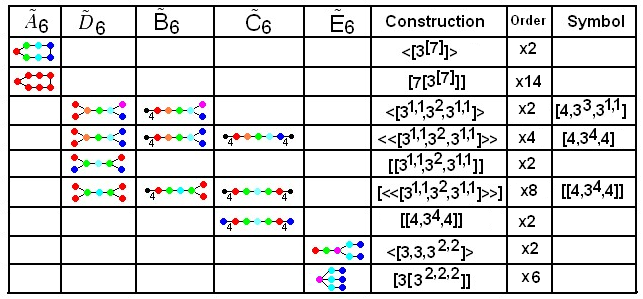 There are five fundamental affine
There are five fundamental affine
Polytope names
{{Polytopes 7-polytopes
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a 7-polytope is a polytope contained by 6-polytope facets. Each 5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
Definition
A 5-polytope is a closed five-dimensional figure with vertices ...
ridge
A ridge or a mountain ridge is a geographical feature consisting of a chain of mountains or hills that form a continuous elevated crest for an extended distance. The sides of the ridge slope away from the narrow top on either side. The line ...
being shared by exactly two 6-polytope
In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.
Definition
A 6-polytope is a closed six-dimensional figure with vertices, edges, faces, cells (3-faces), 4-faces, and 5-faces. A ...
facets.
A uniform 7-polytope is one whose symmetry group is transitive on vertices and whose facets are uniform 6-polytopes.
Regular 7-polytopes
Regular 7-polytopes are represented by theSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to more ...
with u 6-polytopes facets around each 4-face.
There are exactly three such convex regular 7-polytopes:
# - 7-simplex
In 7-dimensional geometry, a 7-simplex is a self-dual regular 7-polytope. It has 8 vertices, 28 edges, 56 triangle faces, 70 tetrahedral cells, 56 5-cell 5-faces, 28 5-simplex 6-faces, and 8 6-simplex 7-faces. Its dihedral angle is cos−1(1/7) ...
# - 7-cube
# - 7-orthoplex
There are no nonconvex regular 7-polytopes.
Characteristics
The topology of any given 7-polytope is defined by its Betti numbers andtorsion coefficient
A torsion spring is a spring that works by twisting its end along its axis; that is, a flexible elastic object that stores mechanical energy when it is twisted. When it is twisted, it exerts a torque in the opposite direction, proportional ...
s.Richeson, D.; ''Euler's Gem: The Polyhedron Formula and the Birth of Topoplogy'', Princeton, 2008.
The value of the Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic (or Euler number, or Euler–Poincaré characteristic) is a topological invariant, a number that describes a topological space ...
used to characterise polyhedra does not generalize usefully to higher dimensions, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.
Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.
Uniform 7-polytopes by fundamental Coxeter groups
Uniform 7-polytopes with reflective symmetry can be generated by these four Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:The A7 family
The A7 family has symmetry of order 40320 (8factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
).
There are 71 (64+8-1) forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. All 71 are enumerated below. Norman Johnson's truncation names are given. Bowers names and acronym are also given for cross-referencing.
See also a list of A7 polytopes
In 7-dimensional geometry, there are 71 uniform 7-polytope, uniform polytopes with A7 symmetry. There is one self-dual regular form, the 7-simplex with 8 vertices.
Each can be visualized as symmetric orthographic projections in Coxeter planes of ...
for symmetric Coxeter plane graphs of these polytopes.
The B7 family
The B7 family has symmetry of order 645120 (7factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
x 27).
There are 127 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. Johnson and Bowers names.
See also a list of B7 polytopes for symmetric Coxeter plane graphs of these polytopes.
The D7 family
The D7 family has symmetry of order 322560 (7factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times (n-1) \times (n-2) \t ...
x 26).
This family has 3×32−1=95 Wythoffian uniform polytopes, generated by marking one or more nodes of the D7 Coxeter-Dynkin diagram. Of these, 63 (2×32−1) are repeated from the B7 family and 32 are unique to this family, listed below. Bowers names and acronym are given for cross-referencing.
See also list of D7 polytopes for Coxeter plane graphs of these polytopes.
The E7 family
The E7 Coxeter group has order 2,903,040. There are 127 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. See also alist of E7 polytopes
In 7-dimensional geometry, there are 127 uniform 7-polytope, uniform polytopes with E7 symmetry. The three simplest forms are the 3_21 polytope, 321, 2_31 polytope, 231, and 1_32 polytope, 132 polytopes, composed of 56, 126, and 576 vertex (geomet ...
for symmetric Coxeter plane graphs of these polytopes.
Regular and uniform honeycombs
 There are five fundamental affine
There are five fundamental affine Coxeter groups
In mathematics, a Coxeter group, named after Harold Scott MacDonald Coxeter, H. S. M. Coxeter, is an group (mathematics), abstract group that admits a group presentation, formal description in terms of Reflection (mathematics), reflections (or Kal ...
and sixteen prismatic groups that generate regular and uniform tessellations in 6-space:
Regular and uniform tessellations include:
* , 17 forms
** Uniform 6-simplex honeycomb
In six-dimensional Euclidean geometry, the 6-simplex honeycomb is a space-filling tessellation (or honeycomb). The tessellation fills space by 6-simplex, rectified 6-simplex, and birectified 6-simplex facets. These facet types occur in proportion ...
:
** Uniform Cyclotruncated 6-simplex honeycomb: t0,1
** Uniform Omnitruncated 6-simplex honeycomb: t0,1,2,3,4,5,6,7
* , ,34,4 71 forms
** Regular 6-cube honeycomb, represented by symbols ,
* , 1,1,33,4 95 forms, 64 shared with , 32 new
** Uniform 6-demicube honeycomb, represented by symbols h = , =
* , 1,1,32,31,1 41 unique ringed permutations, most shared with and , and 6 are new. Coxeter calls the first one a quarter 6-cubic honeycomb.
** =
** =
** =
** =
** =
** =
* : 2,2,2 39 forms
** Uniform 222 honeycomb: represented by symbols ,
** Uniform t4(222) honeycomb: 4r,
** Uniform 0222 honeycomb: ,
** Uniform t2(0222) honeycomb: 2r,
Regular and uniform hyperbolic honeycombs
There are no compact hyperbolic Coxeter groups of rank 7, groups that can generate honeycombs with all finite facets, and a finitevertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
. However, there are 3 paracompact hyperbolic Coxeter groups of rank 7, each generating uniform honeycombs in 6-space as permutations of rings of the Coxeter diagrams.
Notes on the Wythoff construction for the uniform 7-polytopes
The reflective 7-dimensionaluniform polytope
In geometry, a uniform polytope of dimension three or higher is a vertex-transitive polytope bounded by uniform facets. The uniform polytopes in two dimensions are the regular polygons (the definition is different in 2 dimensions to exclude vert ...
s are constructed through a Wythoff construction process, and represented by a Coxeter-Dynkin diagram, where each node represents a mirror. An active mirror is represented by a ringed node. Each combination of active mirrors generates a unique uniform polytope. Uniform polytopes are named in relation to the regular polytopes in each family. Some families have two regular constructors and thus may be named in two equally valid ways.
Here are the primary operators available for constructing and naming the uniform 7-polytopes.
The prismatic forms and bifurcating graphs can use the same truncation indexing notation, but require an explicit numbering system on the nodes for clarity.
References
* T. Gosset: ''On the Regular and Semi-Regular Figures in Space of n Dimensions'', Messenger of Mathematics, Macmillan, 1900 * A. Boole Stott: ''Geometrical deduction of semiregular from regular polytopes and space fillings'', Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910 *H.S.M. Coxeter
Harold Scott MacDonald "Donald" Coxeter, (9 February 1907 – 31 March 2003) was a British and later also Canadian geometer. He is regarded as one of the greatest geometers of the 20th century.
Biography
Coxeter was born in Kensington t ...
:
** H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: ''Uniform Polyhedra'', Philosophical Transactions of the Royal Society of London, Londne, 1954
** H.S.M. Coxeter, ''Regular Polytopes'', 3rd Edition, Dover New York, 1973
* Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, http://www.wiley.com/WileyCDA/WileyTitle/productCd-0471010030.html
** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380-407, MR 2,10** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559-591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3-45* N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966
*
External links
Polytope names
{{Polytopes 7-polytopes