Thomson Problem on:
[Wikipedia]
[Google]
[Amazon]
The objective of the Thomson problem is to determine the minimum electrostatic potential energy configuration of electrons constrained to the surface of a unit sphere that repel each other with a force given by Coulomb's law. The physicist J. J. Thomson posed the problem in 1904 after proposing an atomic model, later called the plum pudding model, based on his knowledge of the existence of negatively charged electrons within neutrally-charged atoms.
Related problems include the study of the geometry of the minimum energy configuration and the study of the large behavior of the minimum energy.
 Mathematically exact minimum energy configurations have been rigorously identified in only a handful of cases.
* For ''N'' = 1, the solution is trivial. The single electron may reside at any point on the surface of the unit sphere. The total energy of the configuration is defined as zero because the electron experiences no electric field due to other sources of charge.
* For ''N'' = 2, the optimal configuration consists of electrons at
Mathematically exact minimum energy configurations have been rigorously identified in only a handful of cases.
* For ''N'' = 1, the solution is trivial. The single electron may reside at any point on the surface of the unit sphere. The total energy of the configuration is defined as zero because the electron experiences no electric field due to other sources of charge.
* For ''N'' = 2, the optimal configuration consists of electrons at
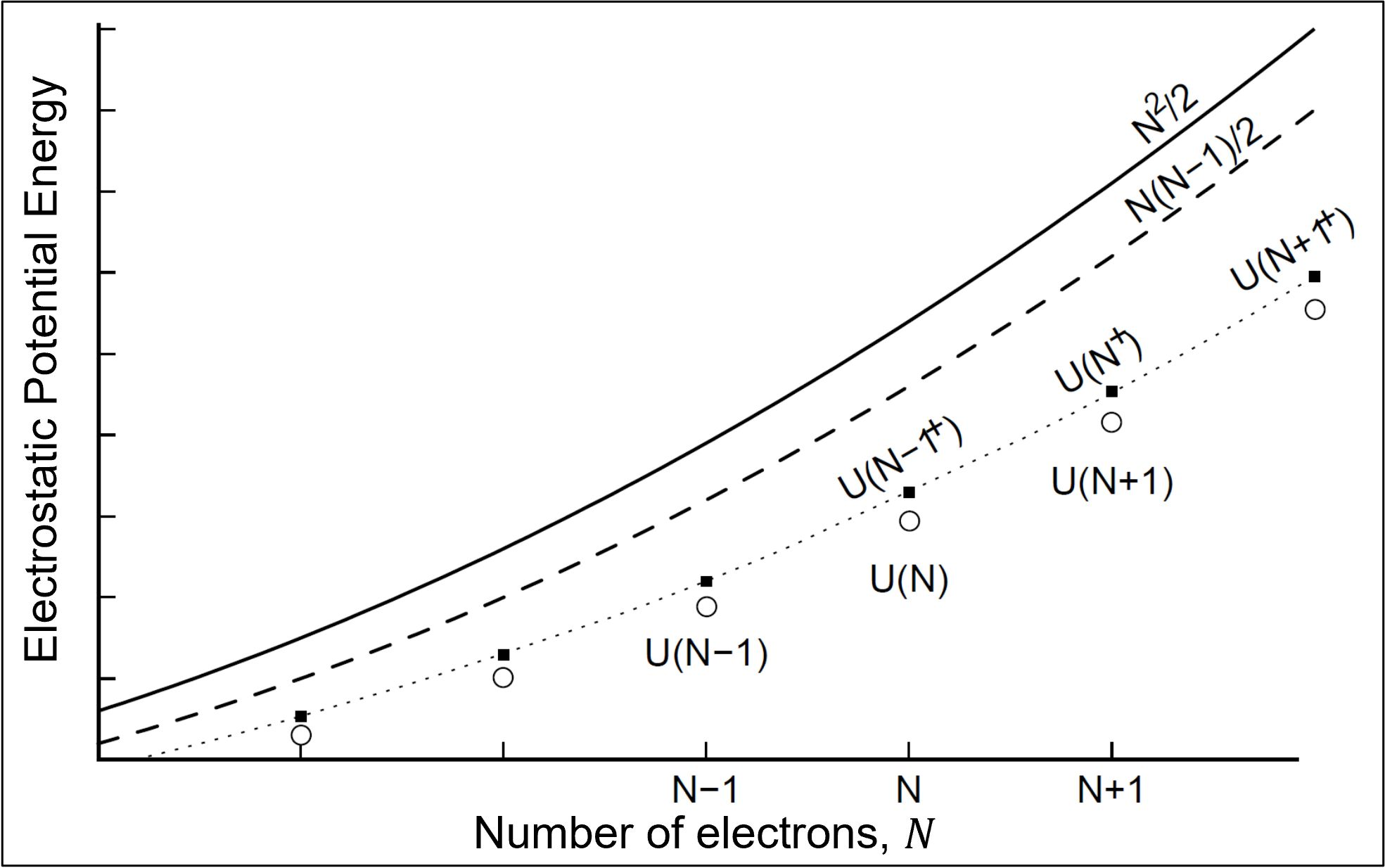 The energy of a continuous spherical shell of charge distributed across its surface is given by
:
and is, in general, greater than the energy of every Thomson problem solution. Note: Here ''N'' is used as a continuous variable that represents the infinitely divisible charge, ''Q'', distributed across the spherical shell. For example, a spherical shell of represents the uniform distribution of a single electron's charge, across the entire shell.
The energy of a continuous spherical shell of charge distributed across its surface is given by
:
and is, in general, greater than the energy of every Thomson problem solution. Note: Here ''N'' is used as a continuous variable that represents the infinitely divisible charge, ''Q'', distributed across the spherical shell. For example, a spherical shell of represents the uniform distribution of a single electron's charge, across the entire shell.
"Min-Energy Configurations of Electrons On A Sphere"
Retrieved 2014-05-01. According to a conjecture, if , ''p'' is the polyhedron formed by the convex hull of ''m'' points, ''q'' is the number of quadrilateral faces of ''p'', then the solution for ''m'' electrons is ''f''(''m''): . (comment: table above must be incorrect since an increase in n must produce a decrease in ''θ, e.g. θ16 < θ17. There are several other examples.)''
Mathematical statement
The electrostatic interaction energy occurring between each pair of electrons of equal charges (, with the elementary charge of an electron) is given by Coulomb's Law, : Here, is the Coulomb constant and is the distance between each pair of electrons located at points on the sphere defined by vectors and , respectively. Simplified units of and are used without loss of generality. Then, : The total electrostatic potential energy of each ''N''-electron configuration may then be expressed as the sum of all pair-wise interaction energies : The global minimization of over all possible configurations of ''N'' distinct points is typically found by numerical minimization algorithms. Thomson's problem is related to the 7th of the eighteen unsolved mathematics problems proposed by the mathematicianSteve Smale
Stephen Smale (born July 15, 1930) is an American mathematician, known for his research in topology, dynamical systems and mathematical economics. He was awarded the Fields Medal in 1966 and spent more than three decades on the mathematics facul ...
— "Distribution of points on the 2-sphere".
The main difference is that in Smale's problem the function to minimise is not the electrostatic potential but a logarithmic potential given by A second difference is that Smale's question is about the asymptotic behaviour of the total potential when the number ''N'' of points goes to infinity, not for concrete values of ''N''.
Example
The solution of the Thomson problem for two electrons is obtained when both electrons are as far apart as possible on opposite sides of the origin, , or :Known exact solutions
 Mathematically exact minimum energy configurations have been rigorously identified in only a handful of cases.
* For ''N'' = 1, the solution is trivial. The single electron may reside at any point on the surface of the unit sphere. The total energy of the configuration is defined as zero because the electron experiences no electric field due to other sources of charge.
* For ''N'' = 2, the optimal configuration consists of electrons at
Mathematically exact minimum energy configurations have been rigorously identified in only a handful of cases.
* For ''N'' = 1, the solution is trivial. The single electron may reside at any point on the surface of the unit sphere. The total energy of the configuration is defined as zero because the electron experiences no electric field due to other sources of charge.
* For ''N'' = 2, the optimal configuration consists of electrons at antipodal point
In mathematics, antipodal points of a sphere are those diametrically opposite to each other (the specific qualities of such a definition are that a line drawn from the one to the other passes through the center of the sphere so forms a true ...
s. This represents the first one-dimensional solution.
* For ''N'' = 3, electrons reside at the vertices of an equilateral triangle about any great circle
In mathematics, a great circle or orthodrome is the circular intersection of a sphere and a plane passing through the sphere's center point.
Any arc of a great circle is a geodesic of the sphere, so that great circles in spherical geomet ...
. The great circle is often considered to define an equator about the sphere and the two points perpendicular to the plane are often considered poles to aid in discussions about the electrostatic configurations of many-''N'' electron solutions. Also, this represents the first two-dimensional solution.
* For ''N'' = 4, electrons reside at the vertices of a regular tetrahedron. Of interest, this represents the first three-dimensional solution.
* For ''N'' = 5, a mathematically rigorous computer-aided solution was reported in 2010 with electrons residing at vertices of a triangular dipyramid. Of interest, it is impossible for any ''N'' solution with five or more electrons to exhibit global equidistance among all pairs of electrons.
* For ''N'' = 6, electrons reside at vertices of a regular octahedron. The configuration may be imagined as four electrons residing at the corners of a square about the equator and the remaining two residing at the poles.
* For ''N'' = 12, electrons reside at the vertices of a regular icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes and . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrica ...
.
Geometric solutions of the Thomson problem for ''N'' = 4, 6, and 12 electrons are Platonic solids whose faces are all congruent equilateral triangles. Numerical solutions for ''N'' = 8 and 20 are not the regular convex polyhedral configurations of the remaining two Platonic solids whose faces are square and pentagonal, respectively.
Generalizations
One can also ask for ground states of particles interacting with arbitrary potentials. To be mathematically precise, let ''f'' be a decreasing real-valued function, and define the energy functional Traditionally, one considers also known as Riesz -kernels. For integrable Riesz kernels see the 1972 work of Landkof. For non-integrable Riesz kernels, thePoppy-seed bagel theorem
In physics, the poppy-seed bagel theorem concerns interacting particles (e.g., electrons) confined to a bounded surface (or body) A when the particles repel each other pairwise with a magnitude that is proportional to the inverse distance between t ...
holds, see the 2004 work of Hardin and Saff. Notable cases include:
* ''α'' = ∞, the Tammes problem (packing);
* ''α'' = 1, the Thomson problem;
* ''α'' = 0, to maximize the product of distances, latterly known as Whyte's problem;
* ''α'' = −1 : maximum average distance problem.
One may also consider configurations of ''N'' points on a sphere of higher dimension. See spherical design.
Solution algorithms
Several algorithms have been applied to this problem. The focus since the millennium has been on local optimization methods applied to the energy function, although random walks have made their appearance: * constrained global optimization (Altschuler et al. 1994), * steepest descent (Claxton and Benson 1966, Erber and Hockney 1991), * random walk (Weinrach et al. 1990), * genetic algorithm (Morris et al. 1996) While the objective is to minimize the global electrostatic potential energy of each ''N''-electron case, several algorithmic starting cases are of interest.Continuous spherical shell charge
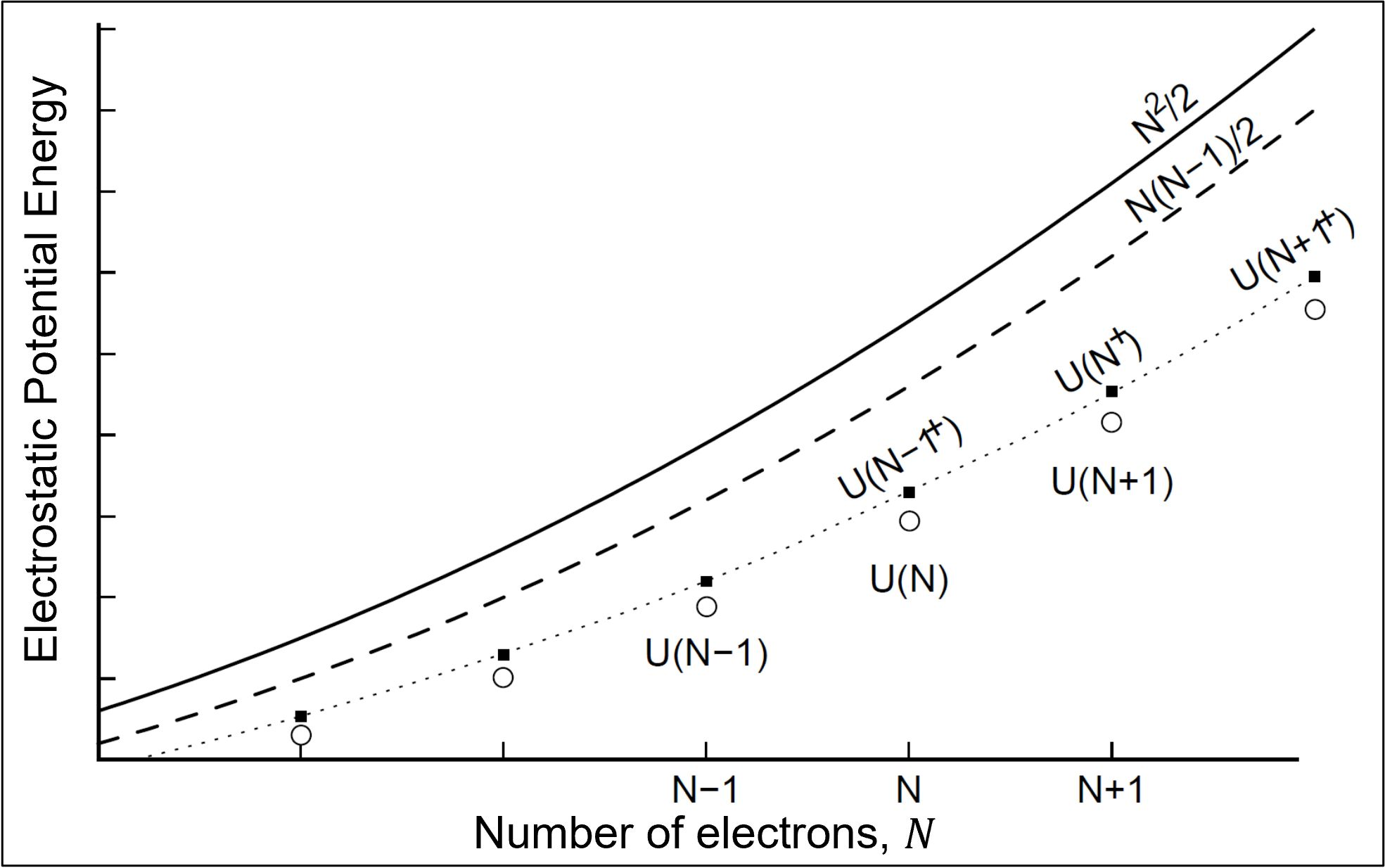 The energy of a continuous spherical shell of charge distributed across its surface is given by
:
and is, in general, greater than the energy of every Thomson problem solution. Note: Here ''N'' is used as a continuous variable that represents the infinitely divisible charge, ''Q'', distributed across the spherical shell. For example, a spherical shell of represents the uniform distribution of a single electron's charge, across the entire shell.
The energy of a continuous spherical shell of charge distributed across its surface is given by
:
and is, in general, greater than the energy of every Thomson problem solution. Note: Here ''N'' is used as a continuous variable that represents the infinitely divisible charge, ''Q'', distributed across the spherical shell. For example, a spherical shell of represents the uniform distribution of a single electron's charge, across the entire shell.
Randomly distributed point charges
The global energy of a system of electrons distributed in a purely random manner across the surface of the sphere is given by : and is, in general, greater than the energy of every Thomson problem solution. Here, ''N'' is a discrete variable that counts the number of electrons in the system. As well,Charge-centered distribution
For every ''N''th solution of the Thomson problem there is an th configuration that includes an electron at the origin of the sphere whose energy is simply the addition of ''N'' to the energy of the ''N''th solution. That is, : Thus, if is known exactly, then is known exactly. In general, is greater than , but is remarkably closer to each th Thomson solution than and . Therefore, the charge-centered distribution represents a smaller "energy gap" to cross to arrive at a solution of each Thomson problem than algorithms that begin with the other two charge configurations.Relations to other scientific problems
The Thomson problem is a natural consequence of J. J. Thomson's plum pudding model in the absence of its uniform positive background charge. Though experimental evidence led to the abandonment of Thomson's plum pudding model as a complete atomic model, irregularities observed in numerical energy solutions of the Thomson problem have been found to correspond with electron shell-filling in naturally occurring atoms throughout theperiodic table
The periodic table, also known as the periodic table of the (chemical) elements, is a rows and columns arrangement of the chemical elements. It is widely used in chemistry, physics, and other sciences, and is generally seen as an icon of ch ...
of elements.
The Thomson problem also plays a role in the study of other physical models including multi-electron bubbles and the surface ordering of liquid metal drops confined in Paul traps.
The generalized Thomson problem arises, for example, in determining arrangements of protein subunits that comprise the shells of spherical virus
A virus is a wikt:submicroscopic, submicroscopic infectious agent that replicates only inside the living Cell (biology), cells of an organism. Viruses infect all life forms, from animals and plants to microorganisms, including bacteria and ...
es. The "particles" in this application are clusters of protein subunits arranged on a shell. Other realizations include regular arrangements of colloid particles in ''colloidosomes'', proposed for encapsulation of active ingredients such as drugs, nutrients or living cells, fullerene patterns of carbon atoms, and VSEPR theory. An example with long-range logarithmic interactions is provided by Abrikosov vortices that form at low temperatures in a superconducting metal shell with a large monopole at its center.
Configurations of smallest known energy
In the following table is the number of points (charges) in a configuration, is the energy, the symmetry type is given in Schönflies notation (see Point groups in three dimensions), and are the positions of the charges. Most symmetry types require the vector sum of the positions (and thus the electric dipole moment) to be zero. It is customary to also consider the polyhedron formed by the convex hull of the points. Thus, is the number of vertices where the given number of edges meet, is the total number of edges, is the number of triangular faces, is the number of quadrilateral faces, and is the smallest angle subtended by vectors associated with the nearest charge pair. Note that the edge lengths are generally not equal. Thus, except in the cases ''N'' = 2, 3, 4, 6, 12, and the geodesic polyhedra, the convex hull is onlytopologically
In mathematics, topology (from the Greek words , and ) is concerned with the properties of a geometric object that are preserved under continuous deformations, such as stretching, twisting, crumpling, and bending; that is, without closing ho ...
equivalent to the figure listed in the last column.
Kevin Brown"Min-Energy Configurations of Electrons On A Sphere"
Retrieved 2014-05-01. According to a conjecture, if , ''p'' is the polyhedron formed by the convex hull of ''m'' points, ''q'' is the number of quadrilateral faces of ''p'', then the solution for ''m'' electrons is ''f''(''m''): . (comment: table above must be incorrect since an increase in n must produce a decrease in ''θ, e.g. θ16 < θ17. There are several other examples.)''
References
Notes
* * * * * * . * * * . * * Configurations reprinted in * * * . Configurations reproduced in * * * This webpage contains many more electron configurations with the lowest known energy: https://www.hars.us. {{DEFAULTSORT:Thomson Problem Electrostatics Electron Circle packing Unsolved problems in mathematics