tetragonal disphenoid

In geometry, a disphenoid () is a tetrahedron whose four faces are congruent acute-angled triangles. It can also be described as a tetrahedron in which every two edges that are opposite each other have equal lengths. Other names for the same shape are isotetrahedron,.
sphenoid,. bisphenoid, isosceles tetrahedron,. equifacial tetrahedron, almost regular tetrahedron, and tetramonohedron.

All the solid angles and vertex figures of a disphenoid are the same, and the sum of the face angles at each vertex is equal to two right angles. However, a disphenoid is not a regular polyhedron, because, in general, its faces are not regular polygons, and its edges have three different lengths.

Special cases and generalizations

If the faces of a disphenoid are equilateral triangles, it is a regular tetrahedron with T_d tetrahedral symmetry, although this is not normally called a disphenoid. When the faces of a disphenoid are isosceles triangles, it is called a tetragonal disphenoid. In this case it has D_2d dihedral symmetry.
A sphenoid with scalene triangles as its faces is called a rhombic disphenoid and it has D₂ dihedral symmetry. Unlike the tetragonal disphenoid, the rhombic disphenoid has no reflection symmetry, so it is chiral.
Both tetragonal disphenoids and rhombic disphenoids are isohedra: as well as being congruent to each other, all of their faces are symmetric to each other.

It is not possible to construct a disphenoid with right triangle or obtuse triangle faces. When right triangles are glued together in the pattern of a disphenoid, they form a flat figure (a doubly-covered rectangle) that does not enclose any volume.. When obtuse triangles are glued in this way, the resulting surface can be folded to form a disphenoid (by Alexandrov's uniqueness theorem) but one with acute triangle faces and with edges that in general do not lie along the edges of the given obtuse triangles.

Two more types of tetrahedron generalize the disphenoid and have similar names.
The digonal disphenoid has faces with two different shapes, both isosceles triangles, with two faces of each shape.
The phyllic disphenoid similarly has faces with two shapes of scalene triangles.

Disphenoids can also be seen as digonal antiprisms or as alternated quadrilateral prisms.

Characterizations

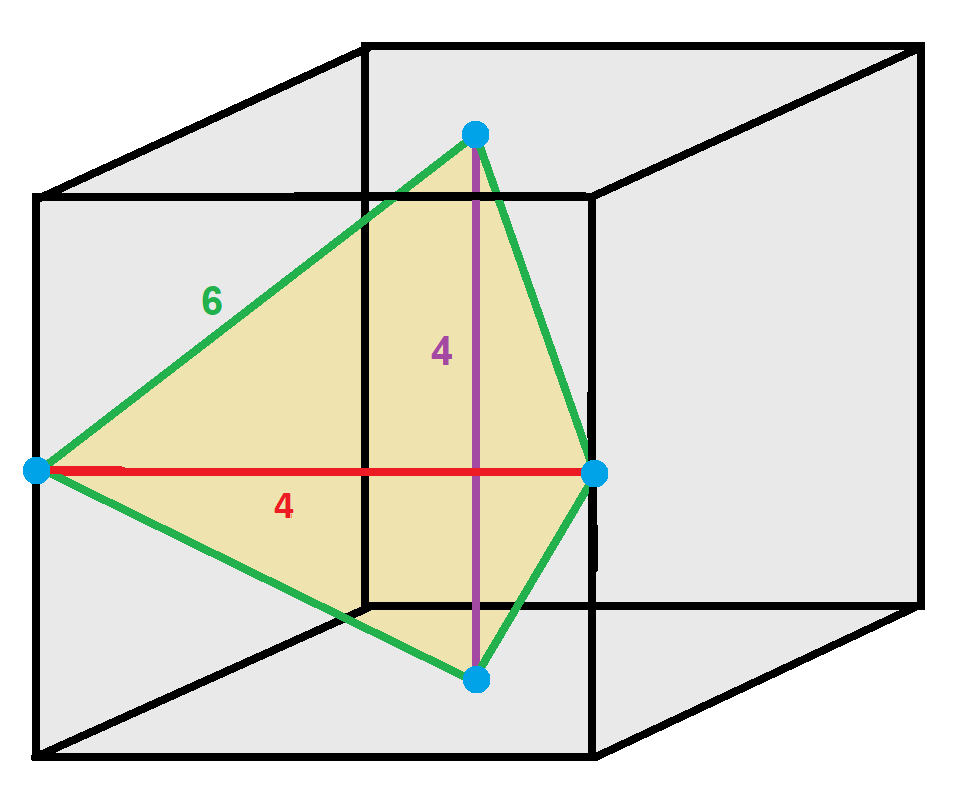
A tetrahedron is a disphenoid if and only if its circumscribed parallelepiped is right-angled.

We also have that a tetrahedron is a disphenoid if and only if the center in the circumscribed sphere and the inscribed sphere coincide..

Another characterization states that if ''d₁'', ''d₂'' and ''d₃'' are the common perpendiculars of ''AB'' and ''CD''; ''AC'' and ''BD''; and ''AD'' and ''BC'' respectively in a tetrahedron ''ABCD'', then the tetrahedron is a disphenoid if and only if ''d₁'', ''d₂'' and ''d₃'' are pairwise perpendicular..

The disphenoids are the only polyhedra having infinitely many non-self-intersecting closed geodesics. On a disphenoid, all closed geodesics are non-self-intersecting.

The disphenoids are the tetrahedra in which all four faces have the same perimeter, the tetrahedra in which all four faces have the same area, and the tetrahedra in which the angular defects of all four vertices equal . They are the polyhedra having a net in the shape of an acute triangle, divided into four similar triangles by segments connecting the edge midpoints..

Metric formulas

The volume of a disphenoid with opposite edges of length ''l'', ''m'' and ''n'' is given by.

:$V=\sqrt.$

The circumscribed sphere has radius (the circumradius)

:$R=\sqrt$

and the inscribed sphere has radius

:$r=\frac$

where ''V'' is the volume of the disphenoid and ''T'' is the area of any face, which is given by Heron's formula. There is also the following interesting relation connecting the volume and the circumradius:

:$\displaystyle 16T^2R^2=l^2m^2n^2+9V^2.$

The squares of the lengths of the bimedians are

:$\tfrac(l^2+m^2-n^2),\quad \tfrac(l^2-m^2+n^2),\quad \tfrac(-l^2+m^2+n^2).$

Other properties

If the four faces of a tetrahedron have the same perimeter, then the tetrahedron is a disphenoid.

If the four faces of a tetrahedron have the same area, then it is a disphenoid.

The centers in the circumscribed and inscribed spheres coincide with the centroid of the disphenoid.

The bimedians are perpendicular to the edges they connect and to each other.

Honeycombs and crystals

Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid. Each of its four faces is an isosceles triangle with edges of lengths , , and 2. It can tessellate space to form the disphenoid tetrahedral honeycomb. As describes, it can be folded without cutting or overlaps from a single sheet of a4 paper. Reprinted in

"Disphenoid" is also used to describe two forms of crystal:

* A wedge-shaped crystal form of the tetragonal or orthorhombic system. It has four triangular faces that are alike and that correspond in position to alternate faces of the tetragonal or orthorhombic dipyramid. It is symmetrical about each of three mutually perpendicular diad axes of symmetry in all classes except the tetragonal-disphenoidal, in which the form is generated by an inverse tetrad axis of symmetry.
*A crystal form bounded by eight scalene triangles arranged in pairs, constituting a tetragonal scalenohedron.

Other uses

Six tetragonal disphenoids attached end-to-end in a ring construct a kaleidocycle, a paper toy that can rotate on 4 sets of faces in a hexagon.

See also

* Irregular tetrahedra
* Orthocentric tetrahedron
* Snub disphenoid - A Johnson solid with 12 equilateral triangle faces and D_2d symmetry.
* Trirectangular tetrahedron

References

External links

Mathematical Analysis of Disphenoid by H C Rajpoot
from Academia.edu
*
*{{Mathworld , urlname=IsoscelesTetrahedron , title=Isosceles tetrahedron

Polyhedra