Surface State on:
[Wikipedia]
[Google]
[Amazon]
Surface states are

 As stated by
As stated by
 The nearly free electron approximation can be used to derive the basic properties of surface states for narrow gap semiconductors. The semi-infinite linear chain model is also useful in this case. However, now the potential along the atomic chain is assumed to vary as a cosine function
whereas at the surface the potential is modeled as a step function of height V0.
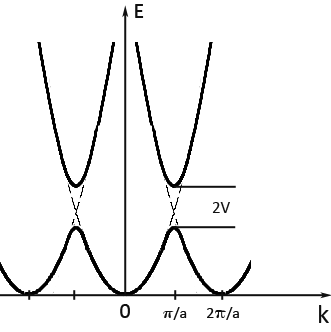
The solutions to the Schrödinger equation must be obtained separately for the two domains z < 0 and z > 0. In the sense of the nearly free electron approximation, the solutions obtained for z < 0 will have plane wave character for wave vectors away from the Brillouin zone boundary , where the dispersion relation will be parabolic, as shown in figure 4.
At the Brillouin zone boundaries, Bragg reflection occurs resulting in a
The nearly free electron approximation can be used to derive the basic properties of surface states for narrow gap semiconductors. The semi-infinite linear chain model is also useful in this case. However, now the potential along the atomic chain is assumed to vary as a cosine function
whereas at the surface the potential is modeled as a step function of height V0.
The solutions to the Schrödinger equation must be obtained separately for the two domains z < 0 and z > 0. In the sense of the nearly free electron approximation, the solutions obtained for z < 0 will have plane wave character for wave vectors away from the Brillouin zone boundary , where the dispersion relation will be parabolic, as shown in figure 4.
At the Brillouin zone boundaries, Bragg reflection occurs resulting in a
 The results for surface states of a monatomic linear chain can readily be generalized to the case of a three-dimensional crystal. Because of the two-dimensional periodicity of the surface lattice, Bloch's theorem must hold for translations parallel to the surface. As a result, the surface states can be written as the product of a Bloch waves with k-values parallel to the surface and a function representing a one-dimensional surface state
:
The energy of this state is increased by a term so that we have
:
where ''m*'' is the effective mass of the electron. The matching conditions at the crystal surface, i.e. at z=0, have to be satisfied for each separately and for each a single, but generally different energy level for the surface state is obtained.
The results for surface states of a monatomic linear chain can readily be generalized to the case of a three-dimensional crystal. Because of the two-dimensional periodicity of the surface lattice, Bloch's theorem must hold for translations parallel to the surface. As a result, the surface states can be written as the product of a Bloch waves with k-values parallel to the surface and a function representing a one-dimensional surface state
:
The energy of this state is increased by a term so that we have
:
where ''m*'' is the effective mass of the electron. The matching conditions at the crystal surface, i.e. at z=0, have to be satisfied for each separately and for each a single, but generally different energy level for the surface state is obtained.
electronic state
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The t ...
s found at the surface
A surface, as the term is most generally used, is the outermost or uppermost layer of a physical object or space. It is the portion or region of the object that can first be perceived by an observer using the senses of sight and touch, and is ...
of materials. They are formed due to the sharp transition from solid material that ends with a surface and are found only at the atom layers closest to the surface. The termination of a material with a surface leads to a change of the electronic band structure
In solid-state physics, the electronic band structure (or simply band structure) of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have (called ''band gaps'' or '' ...
from the bulk material to the vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
. In the weakened potential at the surface, new electronic states can be formed, so called surface states.
Origin at condensed matter interfaces
Bloch's theorem
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
, eigenstates of the single-electron Schrödinger equation with a perfectly periodic potential, a crystal, are Bloch waves
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
:
Here is a function with the same periodicity as the crystal, ''n'' is the band index and k is the wave number. The allowed wave numbers for a given potential are found by applying the usual Born–von Karman cyclic boundary conditions. The termination of a crystal, i.e. the formation of a surface, obviously causes deviation from perfect periodicity. Consequently, if the cyclic boundary conditions are abandoned in the direction normal to the surface the behavior of electrons will deviate from the behavior in the bulk and some modifications of the electronic structure has to be expected.
A simplified model of the crystal potential in one dimension can be sketched as shown in Figure 1. In the crystal, the potential has the periodicity, ''a'', of the lattice while close to the surface it has to somehow attain the value of the vacuum level. The step potential (solid line) shown in Figure 1 is an oversimplification which is mostly convenient for simple model calculations. At a real surface the potential is influenced by image charges and the formation of surface dipoles and it rather looks as indicated by the dashed line.
Given the potential in Figure 1, it can be shown that the one-dimensional single-electron Schrödinger equation gives two qualitatively different types of solutions.
* The first type of states (see figure 2) extends into the crystal and has Bloch character there. These types of solutions correspond to bulk states which terminate in an exponentially decaying tail reaching into the vacuum.
* The second type of states (see figure 3) decays exponentially both into the vacuum and the bulk crystal. These types of solutions correspond to surface states with wave functions localized close to the crystal surface.
The first type of solution can be obtained for both metal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated wit ...
s and semiconductor
A semiconductor is a material with electrical conductivity between that of a conductor and an insulator. Its conductivity can be modified by adding impurities (" doping") to its crystal structure. When two regions with different doping level ...
s. In semiconductors though, the associated eigenenergies have to belong to one of the allowed energy bands. The second type of solution exists in forbidden energy gap of semiconductors as well as in ''local gaps'' of the projected band structure of metals. It can be shown that the energies of these states all lie within the band gap. As a consequence, in the crystal these states are characterized by an imaginary wavenumber
In the physical sciences, the wavenumber (or wave number), also known as repetency, is the spatial frequency of a wave. Ordinary wavenumber is defined as the number of wave cycles divided by length; it is a physical quantity with dimension of ...
leading to an exponential decay
A quantity is subject to exponential decay if it decreases at a rate proportional to its current value. Symbolically, this process can be expressed by the following differential equation, where is the quantity and (lambda
Lambda (; uppe ...
into the bulk.
Shockley states and Tamm states
In the discussion of surface states, one generally distinguishes between Shockley states and Tamm states, named after the American physicistWilliam Shockley
William Bradford Shockley ( ; February 13, 1910 – August 12, 1989) was an American solid-state physicist, electrical engineer, and inventor. He was the manager of a research group at Bell Labs that included John Bardeen and Walter Houser Brat ...
and the Russian physicist Igor Tamm
Igor Yevgenyevich Tamm (; 8 July 1895 – 12 April 1971) was a Soviet Union, Soviet physicist who received the 1958 Nobel Prize in Physics, jointly with Pavel Alekseyevich Cherenkov and Ilya Mikhailovich Frank, for their 1934 discovery and demon ...
. There is no strict physical distinction between the two types of states, but the qualitative character and the mathematical approach used in describing them is different.
* Historically, surface states that arise as solutions to the Schrödinger equation
The Schrödinger equation is a partial differential equation that governs the wave function of a non-relativistic quantum-mechanical system. Its discovery was a significant landmark in the development of quantum mechanics. It is named after E ...
in the framework of the nearly free electron approximation for clean and ideal surfaces, are called Shockley states. Shockley states are thus states that arise due to the change in the electron potential associated solely with the crystal termination. This approach is suited to describe normal metals and some narrow gap semiconductors. Figure 3 shows an example of a Shockley state, derived using the nearly free electron approximation. Within the crystal, Shockley states resemble exponentially-decaying Bloch waves.
* Surface states that are calculated in the framework of a tight-binding model are often called Tamm states. In the tight binding approach, the electronic wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s are usually expressed as linear combinations of atomic orbitals (LCAO). In contrast to the nearly free electron model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quan ...
used to describe the Shockley states, the Tamm states are suitable to describe also transition metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. The lanthanide and actinid ...
s and wide gap semiconductors. Qualitatively, Tamm states resemble localized atomic or molecular orbitals at the surface.
Topological surface states
All materials can be classified by a single number, a topological invariant; this is constructed out of the bulk electronic wave functions, which are integrated in over the Brillouin zone, in a similar way that thegenus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
is calculated in geometric topology
In mathematics, geometric topology is the study of manifolds and Map (mathematics)#Maps as functions, maps between them, particularly embeddings of one manifold into another.
History
Geometric topology as an area distinct from algebraic topo ...
. In certain materials the topological invariant can be changed when certain bulk energy bands invert due to strong spin-orbital coupling. At the interface between an insulator with non-trivial topology, a so-called topological insulator
A topological insulator is a material whose interior behaves as an electrical insulator while its surface behaves as an electrical conductor, meaning that electrons can only move along the surface of the material.
A topological insulator is an ...
, and one with a trivial topology, the interface must become metallic. More over, the surface state must have linear Dirac-like dispersion with a crossing point which is protected by time reversal symmetry. Such a state is predicted to be robust under disorder, and therefore cannot be easily localized.
Shockley states
Surface states in metals
A simple model for the derivation of the basic properties of states at a metal surface is a semi-infinite periodic chain of identical atoms. In this model, the termination of the chain represents the surface, where the potential attains the value V0 of the vacuum in the form of astep function
In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals. Informally speaking, a step function is a piecewise constant function having on ...
, figure 1. Within the crystal the potential is assumed periodic with the periodicity a of the lattice.
The Shockley states are then found as solutions to the one-dimensional single electron Schrödinger equation
:
with the periodic potential
:
where ''l'' is an integer, and ''P'' is the normalization factor.
The solution must be obtained independently for the two domains ''z''<0 and ''z>0'', where at the domain boundary (z=0) the usual conditions on continuity of the wave function and its derivatives are applied. Since the potential is periodic deep inside the crystal, the electronic wave function
In quantum physics, a wave function (or wavefunction) is a mathematical description of the quantum state of an isolated quantum system. The most common symbols for a wave function are the Greek letters and (lower-case and capital psi (letter) ...
s must be Bloch wave
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
s here. The solution in the crystal is then a linear combination of an incoming wave and a wave reflected from the surface. For ''z''>0 the solution will be required to decrease exponentially into the vacuum
:
The wave function for a state at a metal surface is qualitatively shown in figure 2. It is an extended Bloch wave within the crystal with an exponentially decaying tail outside the surface. The consequence of the tail is a deficiency of negative charge density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in co ...
just inside the crystal and an increased negative charge density just outside the surface, leading to the formation of a dipole double layer. The dipole perturbs the potential at the surface leading, for example, to a change of the metal work function
In solid-state physics, the work function (sometimes spelled workfunction) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here "immediately" ...
.
Surface states in semiconductors
standing wave
In physics, a standing wave, also known as a stationary wave, is a wave that oscillates in time but whose peak amplitude profile does not move in space. The peak amplitude of the wave oscillations at any point in space is constant with respect t ...
consisting of a wave with wave vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength) ...
and wave vector .
:
Here is a lattice vector of the reciprocal lattice
Reciprocal lattice is a concept associated with solids with translational symmetry which plays a major role in many areas such as X-ray and electron diffraction as well as the energies of electrons in a solid. It emerges from the Fourier tran ...
(see figure 4).
Since the solutions of interest are close to the Brillouin zone boundary, we set , where ''κ'' is a small quantity. The arbitrary constants ''A'',''B'' are found by substitution into the Schrödinger equation. This leads to the following eigenvalues
:
demonstrating the band splitting at the edges of the Brillouin zone
In mathematics and solid state physics, the first Brillouin zone (named after Léon Brillouin) is a uniquely defined primitive cell in reciprocal space
Reciprocal lattice is a concept associated with solids with translational symmetry whic ...
, where the width of the forbidden gap is given by 2V. The electronic wave functions deep inside the crystal, attributed to the different bands are given by
:
Where ''C'' is a normalization constant.
Near the surface at ''z = 0'',
the bulk solution has to be fitted to an exponentially decaying solution, which is compatible with the constant potential ''V0''.
:
It can be shown that the matching conditions can be fulfilled for every possible energy eigenvalue
In linear algebra, an eigenvector ( ) or characteristic vector is a vector that has its direction unchanged (or reversed) by a given linear transformation. More precisely, an eigenvector \mathbf v of a linear transformation T is scaled by a ...
which lies in the allowed band. As in the case for metals, this type of solution represents standing Bloch waves extending into the crystal which spill over into the vacuum
A vacuum (: vacuums or vacua) is space devoid of matter. The word is derived from the Latin adjective (neuter ) meaning "vacant" or "void". An approximation to such vacuum is a region with a gaseous pressure much less than atmospheric pressur ...
at the surface. A qualitative plot of the wave function is shown in figure 2.
If imaginary values of ''κ'' are considered, i.e. ''κ = - i·q'' for ''z ≤ 0'' and one defines
:
one obtains solutions with a decaying amplitude into the crystal
:
The energy eigenvalues are given by
:
E is real for large negative z, as required. Also in the range all energies of the surface states fall into the forbidden gap. The complete solution is again found by matching the bulk solution to the exponentially decaying vacuum solution. The result is a state localized at the surface decaying both into the crystal and the vacuum. A qualitative plot is shown in figure 3.
Surface states of a three-dimensional crystal
True surface states and surface resonances
A surface state is described by the energy and its wave vector parallel to the surface, while a bulk state is characterized by both and wave numbers. In the two-dimensionalBrillouin zone
In mathematics and solid state physics, the first Brillouin zone (named after Léon Brillouin) is a uniquely defined primitive cell in reciprocal space
Reciprocal lattice is a concept associated with solids with translational symmetry whic ...
of the surface, for each value of therefore a rod of is extending into the three-dimensional Brillouin zone of the Bulk. Bulk energy band
In solid-state physics, the electronic band structure (or simply band structure) of a solid describes the range of energy levels that electrons may have within it, as well as the ranges of energy that they may not have (called ''band gaps'' or '' ...
s that are being cut by these rods allow states that penetrate deep into the crystal. One therefore generally distinguishes between true surface states and surface resonances. True surface states are characterized by energy bands that are not degenerate with bulk energy bands. These states exist in the forbidden energy gap only and are therefore localized at the surface, similar to the picture given in figure 3. At energies where a surface and a bulk state are degenerate, the surface and the bulk state can mix, forming a surface resonance. Such a state can propagate deep into the bulk, similar to Bloch wave
In condensed matter physics, Bloch's theorem states that solutions to the Schrödinger equation in a periodic potential can be expressed as plane waves modulated by periodic functions. The theorem is named after the Swiss physicist Felix Bloch, ...
s, while retaining an enhanced amplitude close to the surface.
Tamm states
Surface states that are calculated in the framework of a tight-binding model are often called Tamm states. In the tight binding approach, the electronic wave functions are usually expressed as alinear combination of atomic orbitals
A linear combination of atomic orbitals or LCAO is a quantum superposition of atomic orbitals and a technique for calculating molecular orbitals in quantum chemistry. In quantum mechanics, electron configurations of atoms are described as wavefunc ...
(LCAO), see figure 5. In this picture, it is easy to comprehend that the existence of a surface will give rise to surface states with energies different from the energies of the bulk states: Since the atoms residing in the topmost surface layer are missing their bonding partners on one side, their orbitals have less overlap with the orbitals of neighboring atoms. The splitting and shifting of energy levels of the atoms forming the crystal is therefore smaller at the surface than in the bulk.
If a particular orbital is responsible for the chemical bonding, e.g. the ''sp3'' hybrid in Si or Ge, it is strongly affected by the presence of the surface, bonds are broken, and the remaining lobes of the orbital stick out from the surface. They are called dangling bond
In chemistry, a dangling bond is an unsatisfied Valence (chemistry), valence on an immobilized atom. An atom with a dangling bond is also referred to as an immobilized free radical or an immobilized radical, a reference to its structural and chemi ...
s. The energy levels of such states are expected to significantly shift from the bulk values.
In contrast to the nearly free electron model used to describe the Shockley states, the Tamm states are suitable to describe also transition metal
In chemistry, a transition metal (or transition element) is a chemical element in the d-block of the periodic table (groups 3 to 12), though the elements of group 12 (and less often group 3) are sometimes excluded. The lanthanide and actinid ...
s and wide-bandgap semiconductor
Wide-bandgap semiconductors (also known as WBG semiconductors or WBGSs) are semiconductor materials which have a larger band gap than conventional semiconductors. Conventional semiconductors like silicon and selenium have a bandgap in the range ...
s.
Extrinsic surface states
Surface states originating from clean and well ordered surfaces are usually called ''intrinsic
In science and engineering, an intrinsic property is a property of a specified subject that exists itself or within the subject. An extrinsic property is not essential or inherent to the subject that is being characterized. For example, mass i ...
''. These states include states originating from reconstructed surfaces, where the two-dimensional translational symmetry
In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation (without rotation). Discrete translational symmetry is invariant under discrete translation.
Analogously, an operato ...
gives rise to the band structure in the k space of the surface.
''Extrinsic
In science and engineering, an intrinsic property is a property of a specified subject that exists itself or within the subject. An extrinsic property is not essential or inherent to the subject that is being characterized. For example, mass i ...
'' surface states are usually defined as states not originating from a clean and well ordered surface. Surfaces that fit into the category ''extrinsic'' are:
# Surfaces with defects, where the translational symmetry of the surface is broken.
# Surfaces with adsorbates
# Interfaces between two materials, such as a semiconductor-oxide or semiconductor-metal interface
# Interfaces between solid and liquid phases.
Generally, ''extrinsic'' surface states cannot easily be characterized in terms of their chemical, physical or structural properties.
Experimental observation
Angle resolved photoemission spectroscopy
An experimental technique to measure the dispersion of surface states is angle resolved photoemission spectroscopy (ARPES
Angle-resolved photoemission spectroscopy (ARPES) is an experimental technique used in condensed matter physics to probe the allowed energies and momenta of the electrons in a material, usually a crystalline solid. It is based on the photoelec ...
) or angle resolved ultraviolet photoelectron spectroscopy
Ultraviolet photoelectron spectroscopy (UPS) refers to the measurement of kinetic energy spectra of photoelectrons emitted by molecules that have absorbed ultraviolet photons, in order to determine molecular orbital energies in the valence regio ...
(ARUPS).
Scanning tunneling microscopy
The surface state dispersion can be measured using ascanning tunneling microscope
A scanning tunneling microscope (STM) is a type of scanning probe microscope used for imaging surfaces at the atomic level. Its development in 1981 earned its inventors, Gerd Binnig and Heinrich Rohrer, then at IBM Zürich, the Nobel Prize in ...
; in these experiments, periodic modulations in the surface state density, which arise from scattering off of surface impurities or step edges, are measured by an STM tip at a given bias voltage. The wavevector versus bias (energy) of the surface state electrons can be fit to a free-electron model with effective mass and surface state onset energy.
A recent new theory
A naturally simple but fundamental question is how many surface states are in a band gap in a one-dimensional crystal of length ( is the potential period, and is a positive integer)? A well-accepted concept proposed by Fowler first in 1933, then written in Seitz's classic book that "in a finite one-dimensional crystal the surface states occur in pairs, one state being associated with each end of the crystal." Such a concept seemly was never doubted since then for nearly a century, as shown, for example, in. However, a recent new investigation gives an entirely different answer. The investigation tries to understand electronic states in ideal crystals of finite size based on the mathematical theory of periodic differential equations. This theory provides some fundamental new understandings of those electronic states, including surface states. The theory found that a one-dimensional finite crystal with two ends at and ''always has one and only one state whose energy and properties depend on but not for each band gap.'' This state is either a band-edge state or a surface state in the band gap(see, Particle in a one-dimensional lattice,Particle in a box
In quantum mechanics, the particle in a box model (also known as the infinite potential well or the infinite square well) describes the movement of a free particle in a small space surrounded by impenetrable barriers. The model is mainly used a ...
).
Numerical calculations have confirmed such findings.
Further, these behaviors have been seen in different one-dimensional systems, such as in.
Therefore:
*The fundamental property of a surface state is that its existence and properties depend on the location of the periodicity truncation.
*Truncation of the lattice's periodic potential may or may not lead to a surface state in a band gap.
*An ideal one-dimensional crystal of finite length with two ends can have, at most, ''only one surface state at one end'' in each band gap.
Further investigations extended to multi-dimensional cases found that
*An ideal simple three-dimensional finite crystal may have vertex-like, edge-like, surface-like, and bulk-like states.
*A surface state is always in a band gap is only valid for one-dimensional cases.
References
{{reflist, 2 Materials science Electronic band structures Semiconductor structures