Steiner's Porism on:
[Wikipedia]
[Google]
[Amazon]
In
Image:Steiner_chain_7mer.svg, The 7 circles of this Steiner chain (black) are externally tangent to the inner given circle (red) but internally tangent to the outer given circle (blue).
Image:Steiner_chain_7mer_all_external.svg, The 7 circles of this Steiner chain (black) are externally tangent to both given circles (red and blue), which lie outside one another.
Image:Steiner_chain_8mer_all_but_one_external.svg, Seven of the 8 circles of this Steiner chain (black) are externally tangent to both given circles (red and blue); the 8th circle is internally tangent to both.
The two given circles ''α'' and ''β'' cannot intersect; hence, the smaller given circle must lie inside or outside the larger. The circles are usually shown as an
Image:Steiner_chain_9mer_annular.svg, Closed Steiner chain of nine circles. The 1st and 9th circles are tangent.
Image:Steiner_chain_open_9mer.svg, Open Steiner chain of nine circles. The 1st and 9th circles overlap.
Image:Steiner_chain_double_17mer.svg, Multicyclic Steiner chain of 17 circles in 2 wraps. The 1st and 17th circles touch.
The two given circles ''α'' and ''β'' touch the ''n'' circles of the Steiner chain, but each circle ''C''''k'' of a Steiner chain touches only four circles: ''α'', ''β'', and its two neighbors, ''C''''k''−1 and ''C''''k''+1. By default, Steiner chains are assumed to be ''closed'', i.e., the first and last circles are tangent to one another. By contrast, an ''open'' Steiner chain is one in which the first and last circles, ''C''1 and ''C''''n'', are not tangent to one another; these circles are tangent only to ''three'' circles. Multicyclic Steiner chains wrap around the inner circle more than once before closing, i.e., before being tangent to the initial circle.
Closed Steiner chains are the systems of circles obtained as the
Image:Steiner_chain_3mer_annular.svg,
Image:Steiner_chain_6mer_annular.svg,
Image:Steiner_chain_9mer_annular.svg,
Image:Steiner_chain_12mer_annular.svg,
Image:Steiner_chain_20mer_annular.svg,
 The simplest type of Steiner chain is a closed chain of ''n'' circles of equal size surrounding an inscribed circle of radius ''r''; the chain of circles is itself surrounded by a circumscribed circle of radius ''R''. The inscribed and circumscribed given circles are concentric, and the Steiner-chain circles lie in the
The simplest type of Steiner chain is a closed chain of ''n'' circles of equal size surrounding an inscribed circle of radius ''r''; the chain of circles is itself surrounded by a circumscribed circle of radius ''R''. The inscribed and circumscribed given circles are concentric, and the Steiner-chain circles lie in the
File:Steiner chain 9mer annular angle2.svg, Two circles (pink and cyan) that are internally tangent to both given circles and whose centers are collinear with the center of the given circles intersect at the angle 2''θ''.
File:Steiner chain 9mer annular angle4.svg, Under inversion, these lines and circles become circles with the same intersection angle, 2''θ''. The gold circles intersect the two given circles at right angles, i.e., orthogonally.
File:Steiner chain 6mer tangent circles.svg, The circles passing through the mutual tangent points of the Steiner-chain circles are orthogonal to the two given circles and intersect one another at multiples of the angle 2''θ''.
File:Steiner chain 6mer orthogonal circles.svg, The circles passing through the tangent points of the Steiner-chain circles with the two given circles are orthogonal to the latter and intersect at multiples of the angle 2''θ''.
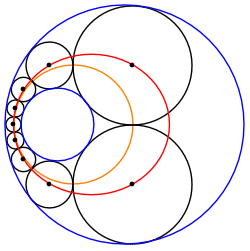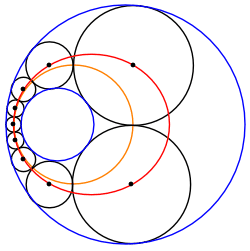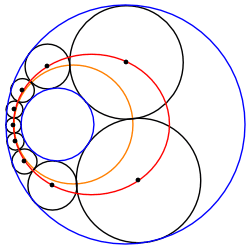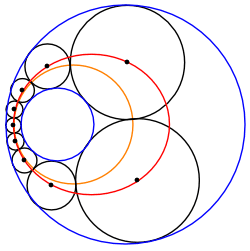 A Steiner chain between two non-intersecting circles can always be transformed into another Steiner chain of equally sized circles sandwiched between two concentric circles. Therefore, any such Steiner chain belongs to an infinite family of Steiner chains related by rotation of the transformed chain about O, the common center of the transformed bounding circles.
A Steiner chain between two non-intersecting circles can always be transformed into another Steiner chain of equally sized circles sandwiched between two concentric circles. Therefore, any such Steiner chain belongs to an infinite family of Steiner chains related by rotation of the transformed chain about O, the common center of the transformed bounding circles.
Image:Steiner_chain_4mer_outside3.svg, Steiner chain with the two given circles shown in red and blue.
Image:Steiner_chain_4mer_outside2.svg, Same set of circles, but with a different choice of given circles.
Image:Steiner_chain_4mer_outside.svg, Same set of circles, but with yet another choice of given circles.
If a Steiner chain has an even number of circles, then any two diametrically opposite circles in the chain can be taken as the two given circles of a new Steiner chain to which the original circles belong. If the original Steiner chain has ''n'' circles in ''m'' wraps, and the new chain has ''p'' circles in ''q'' wraps, then the equation holds
:
A simple example occurs for Steiner chains of four circles (''n'' = 4) and one wrap (''m'' = 1). In this case, the given circles and the Steiner-chain circles are equivalent in that both types of circles are tangent to four others; more generally, Steiner-chain circles are tangent to four circles, but the two given circles are tangent to ''n'' circles. In this case, any pair of opposite members of the Steiner chain may be selected as the given circles of another Steiner chain that involves the original given circles. Since ''m'' = ''p'' = 1 and ''n'' = ''q'' = 4, Steiner's equation is satisfied:
:
 The simplest generalization of a Steiner chain is to allow the given circles to touch or intersect one another. In the former case, this corresponds to a
The simplest generalization of a Steiner chain is to allow the given circles to touch or intersect one another. In the former case, this corresponds to a
Interactive animation of a Steiner chain
Interactive Applet
by Michael Borcherds showing an animation of Steiner's Chain with a variable number of circles made wit
GeoGebra
Circles Inversive geometry Circle packing
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a Steiner chain is a set of circles, all of which are tangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. Mo ...
to two given non-intersecting circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
s (blue and red in Figure 1), where is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usual ''closed'' Steiner chains, the first and last (-th) circles are also tangent to each other; by contrast, in ''open'' Steiner chains, they need not be. The given circles and do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola
In mathematics, a hyperbola (; pl. hyperbolas or hyperbolae ; adj. hyperbolic ) is a type of smooth curve lying in a plane, defined by its geometric properties or by equations for which it is the solution set. A hyperbola has two pieces, c ...
, respectively.
Steiner chains are named after Jakob Steiner
Jakob Steiner (18 March 1796 – 1 April 1863) was a Swiss mathematician who worked primarily in geometry.
Life
Steiner was born in the village of Utzenstorf, Canton of Bern. At 18, he became a pupil of Heinrich Pestalozzi and afterwards s ...
, who defined them in the 19th century and discovered many of their properties. A fundamental result is ''Steiner's porism
A porism is a mathematical proposition or corollary. It has been used to refer to a direct consequence of a proof, analogous to how a corollary refers to a direct consequence of a theorem. In modern usage, it is a relationship that holds for an i ...
'', which states:
::If at least one closed Steiner chain of circles exists for two given circles and , then there is an infinite number of closed Steiner chains of circles; and any circle tangent to and in the same way is a member of such a chain.
The method of circle inversion
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
is helpful in treating Steiner chains. Since it preserves tangencies, angles and circles, inversion transforms one Steiner chain into another of the same number of circles. One particular choice of inversion transforms the given circles and into concentric circles; in this case, all the circles of the Steiner chain have the same size and can "roll" around in the annulus
Annulus (or anulus) or annular indicates a ring- or donut-shaped area or structure. It may refer to:
Human anatomy
* ''Anulus fibrosus disci intervertebralis'', spinal structure
* Annulus of Zinn, a.k.a. annular tendon or ''anulus tendineus co ...
between the circles similar to ball bearing
A ball bearing is a type of rolling-element bearing that uses balls to maintain the separation between the bearing races.
The purpose of a ball bearing is to reduce rotational friction and support radial and axial loads. It achieves this ...
s. This standard configuration allows several properties of Steiner chains to be derived, e.g., its points of tangencies always lie on a circle. Several generalizations of Steiner chains exist, most notably Soddy's hexlet and Pappus chain
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.
Construction
The arbelos is defined by two circles, ''C''U and ''C''V, which are tangent at the poin ...
s.
Definitions and types of tangency
annulus
Annulus (or anulus) or annular indicates a ring- or donut-shaped area or structure. It may refer to:
Human anatomy
* ''Anulus fibrosus disci intervertebralis'', spinal structure
* Annulus of Zinn, a.k.a. annular tendon or ''anulus tendineus co ...
, i.e., with the smaller given circle inside the larger one. In this configuration, the Steiner-chain circles are externally tangent to the inner given circle and internally tangent to the outer circle. However, the smaller circle may also lie completely outside the larger one (Figure 2). The black circles of Figure 2 satisfy the conditions for a closed Steiner chain: they are all tangent to the two given circles and each is tangent to its neighbors in the chain. In this configuration, the Steiner-chain circles have the same type of tangency to both given circles, either externally or internally tangent to both. If the two given circles are tangent at a point, the Steiner chain becomes an infinite Pappus chain
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.
Construction
The arbelos is defined by two circles, ''C''U and ''C''V, which are tangent at the poin ...
, which is often discussed in the context of the arbelos
In geometry, an arbelos is a plane region bounded by three semicircles with three apexes such that each corner of each semicircle is shared with one of the others (connected), all on the same side of a straight line (the ''baseline'') that conta ...
(''shoemaker's knife''), a geometric figure made from three circles. There is no general name for a sequence of circles tangent to two given circles that intersect at two points.
Closed, open and multi-cyclic
circle packing theorem
The circle packing theorem (also known as the Koebe–Andreev–Thurston theorem) describes the possible tangency relations between circles in the plane whose interiors are disjoint. A circle packing is a connected collection of circles (in gen ...
representation of a bipyramid
A (symmetric) -gonal bipyramid or dipyramid is a polyhedron formed by joining an -gonal pyramid and its mirror image base-to-base. An -gonal bipyramid has triangle faces, edges, and vertices.
The "-gonal" in the name of a bipyramid does ...
.
Annular case and feasibility criterion
annulus
Annulus (or anulus) or annular indicates a ring- or donut-shaped area or structure. It may refer to:
Human anatomy
* ''Anulus fibrosus disci intervertebralis'', spinal structure
* Annulus of Zinn, a.k.a. annular tendon or ''anulus tendineus co ...
between them. By symmetry, the angle 2''θ'' between the centers of the Steiner-chain circles is 360°/''n''. Because Steiner chain circles are tangent to one another, the distance between their centers equals the sum of their radii, here twice their radius ''ρ''. The bisector (green in Figure) creates two right triangles, with a central angle of . The sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is opp ...
of this angle can be written as the length of its opposite segment, divided by the hypotenuse of the right triangle
:
Since ''θ'' is known from ''n'', this provides an equation for the unknown radius ''ρ'' of the Steiner-chain circles
:
The tangent points of a Steiner chain circle with the inner and outer given circles lie on a line that pass through their common center; hence, the outer radius .
These equations provide a criterion for the feasibility of a Steiner chain for two given concentric circles. A closed Steiner chain of ''n'' circles requires that the ratio of radii ''R''/''r'' of the given circles equal exactly
:
As shown below, this ratio-of-radii criterion for concentric given circles can be extended to all types of given circles by the inversive distance ''δ'' of the two given circles. For concentric circles, this distance is defined as a logarithm of their ratio of radii
:
Using the solution for concentric circles, the general criterion for a Steiner chain of ''n'' circles can be written
:
If a multicyclic annular Steiner chain has ''n'' total circles and wraps around ''m'' times before closing, the angle between Steiner-chain circles equals
:
In other respects, the feasibility criterion is unchanged.
Properties under inversion
Circle inversion
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
transforms one Steiner chain into another with the same number of circles.
In the transformed chain, the tangent points between adjacent circles of the Steiner chain all lie on a circle, namely the concentric circle midway between the two fixed concentric circles. Since tangencies and circles are preserved under inversion, this property of all tangencies lying on a circle is also true in the original chain. This property is also shared with the Pappus chain
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.
Construction
The arbelos is defined by two circles, ''C''U and ''C''V, which are tangent at the poin ...
of circles, which can be construed as a special limiting case of the Steiner chain.
In the transformed chain, the tangent lines from O to the Steiner chain circles are separated by equal angles. In the original chain, this corresponds to equal angles between the tangent circles that pass through the center of inversion used to transform the original circles into a concentric pair.
In the transformed chain, the ''n'' lines connecting the pairs of tangent points of the Steiner circles with the concentric circles all pass through O, the common center. Similarly, the ''n'' lines tangent to each pair of adjacent circles in the Steiner chain also pass through O. Since lines through the center of inversion are invariant under inversion, and since tangency and concurrence are preserved under inversion, the 2''n'' lines connecting the corresponding points in the original chain also pass through a single point, O.
Infinite family
 A Steiner chain between two non-intersecting circles can always be transformed into another Steiner chain of equally sized circles sandwiched between two concentric circles. Therefore, any such Steiner chain belongs to an infinite family of Steiner chains related by rotation of the transformed chain about O, the common center of the transformed bounding circles.
A Steiner chain between two non-intersecting circles can always be transformed into another Steiner chain of equally sized circles sandwiched between two concentric circles. Therefore, any such Steiner chain belongs to an infinite family of Steiner chains related by rotation of the transformed chain about O, the common center of the transformed bounding circles.
Elliptical/hyperbolic locus of centers
The centers of the circles of a Steiner chain lie on aconic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a ...
. For example, if the smaller given circle lies within the larger, the centers lie on an ellipse. This is true for any set of circles that are internally tangent to one given circle and externally tangent to the other; such systems of circles appear in the Pappus chain
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.
Construction
The arbelos is defined by two circles, ''C''U and ''C''V, which are tangent at the poin ...
, the problem of Apollonius
In Euclidean plane geometry, Apollonius's problem is to construct circles that are tangent to three given circles in a plane (Figure 1). Apollonius of Perga (c. 262 190 BC) posed and solved this famous problem in his work (', "Tangencie ...
, and the three-dimensional Soddy's hexlet. Similarly, if some circles of the Steiner chain are externally tangent to both given circles, their centers must lie on a hyperbola, whereas those that are internally tangent to both lie on a different hyperbola.
The circles of the Steiner chain are tangent to two fixed circles, denoted here as ''α'' and ''β'', where ''β'' is enclosed by ''α''. Let the radii of these two circles be denoted as ''r''''α'' and ''r''''β'', respectively, and let their respective centers be the points A and B. Let the radius, diameter and center point of the ''k''th circle of the Steiner chain be denoted as ''r''''k'', ''d''''k'' and P''k'', respectively.
All the centers of the circles in the Steiner chain are located on a common ellipse, for the following reason.Ogilvy, p. 57. The sum of the distances from the center point of the ''k''th circle of the Steiner chain to the two centers A and B of the fixed circles equals a constant
:
Thus, for all the centers of the circles of the Steiner chain, the sum of distances to A and B equals the same constant, ''r''''α'' + ''r''''β''. This defines an ellipse, whose two foci
Focus, or its plural form foci may refer to:
Arts
* Focus or Focus Festival, former name of the Adelaide Fringe arts festival in South Australia Film
*''Focus'', a 1962 TV film starring James Whitmore
* ''Focus'' (2001 film), a 2001 film based ...
are the points A and B, the centers of the circles, ''α'' and ''β'', that sandwich the Steiner chain of circles.
The sum of distances to the foci equals twice the semi-major axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the lo ...
''a'' of an ellipse; hence,
:
Let ''p'' equal the distance between the foci, A and B. Then, the eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off- center, in geometry
* Eccentricity (graph theory) of a ...
''e'' is defined by 2 ''ae'' = ''p'', or
:
From these parameters, the semi-minor axis
In geometry, the major axis of an ellipse is its longest diameter: a line segment that runs through the center and both foci, with ends at the two most widely separated points of the perimeter. The semi-major axis (major semiaxis) is the lon ...
''b'' and the semi-latus rectum ''L'' can be determined
:
:
Therefore, the ellipse can be described by an equation in terms of its distance ''d'' to one focus
:
where ''θ'' is the angle with the line joining the two foci.
Conjugate chains
Generalizations
 The simplest generalization of a Steiner chain is to allow the given circles to touch or intersect one another. In the former case, this corresponds to a
The simplest generalization of a Steiner chain is to allow the given circles to touch or intersect one another. In the former case, this corresponds to a Pappus chain
In geometry, the Pappus chain is a ring of circles between two tangent circles investigated by Pappus of Alexandria in the 3rd century AD.
Construction
The arbelos is defined by two circles, ''C''U and ''C''V, which are tangent at the poin ...
, which has an infinite number of circles.
Soddy's hexlet is a three-dimensional generalization of a Steiner chain of six circles. The centers of the six spheres (the ''hexlet'') travel along the same ellipse as do the centers of the corresponding Steiner chain. The envelope of the hexlet spheres is a Dupin cyclide
In mathematics, a Dupin cyclide or cyclide of Dupin is any geometric inversion of a standard torus, cylinder or double cone. In particular, these latter are themselves examples of Dupin cyclides. They were discovered by (and named after) Charles ...
, the inversion of a torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle.
If the axis of revolution does not ...
. The six spheres are not only tangent to the inner and outer sphere, but also to two other spheres, centered above and below the plane of the hexlet centers.
Multiple rings of Steiner chains are another generalization. An ordinary Steiner chain is obtained by inverting an annular chain of tangent circles bounded by two concentric circles. This may be generalized to inverting three or more concentric circles that sandwich annular chains of tangent circles.
Hierarchical Steiner chains are yet another generalization. If the two given circles of an ordinary Steiner chain are nested, i.e., if one lies entirely within the other, then the larger given circle circumscribes the Steiner-chain circles. In a hierarchical Steiner chain, each circle of a Steiner chain is itself the circumscribing given circle of another Steiner chain within it; this process may be repeated indefinitely, forming a fractal
In mathematics, a fractal is a geometric shape containing detailed structure at arbitrarily small scales, usually having a fractal dimension strictly exceeding the topological dimension. Many fractals appear similar at various scales, as il ...
.
See also
* Poncelet porism *Ford circles
In mathematics, a Ford circle is a circle with center at (p/q,1/(2q^2)) and radius 1/(2q^2), where p/q is an irreducible fraction, i.e. p and q are coprime integers. Each Ford circle is tangent to the horizontal axis y=0, and any two Ford c ...
*Apollonian gasket
In mathematics, an Apollonian gasket or Apollonian net is a fractal generated by starting with a triple of circles, each tangent to the other two, and successively filling in more circles, each tangent to another three. It is named after Greek ma ...
Notes
References
Bibliography
* * * *Further reading
* * *External links
*{{mathworld, urlname=SteinerChain, title=Steiner ChainInteractive animation of a Steiner chain
CodePen
CodePen is an online community for testing and showcasing user-created HTML, CSS and JavaScript code snippets. It functions as an online code editor and open-source
Open source is source code that is made freely available for possible modif ...
Interactive Applet
by Michael Borcherds showing an animation of Steiner's Chain with a variable number of circles made wit
GeoGebra
Circles Inversive geometry Circle packing