Squarewave on:
[Wikipedia]
[Google]
[Amazon]
A square wave is a non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions between minimum and maximum are instantaneous.
The square wave is a special case of a pulse wave which allows arbitrary durations at minimum and maximum amplitudes. The ratio of the high period to the total period of a pulse wave is called the

 Using Fourier expansion with cycle frequency over time , an ideal square wave with an amplitude of 1 can be represented as an infinite sum of sinusoidal waves:
The ideal square wave contains only components of odd-integer
Using Fourier expansion with cycle frequency over time , an ideal square wave with an amplitude of 1 can be represented as an infinite sum of sinusoidal waves:
The ideal square wave contains only components of odd-integer 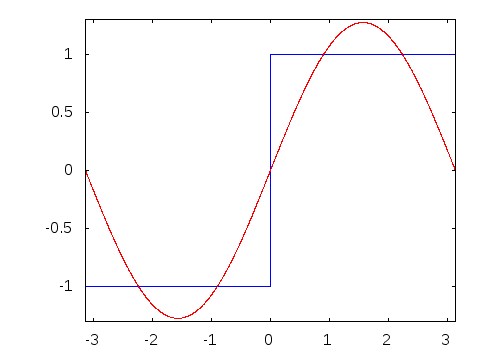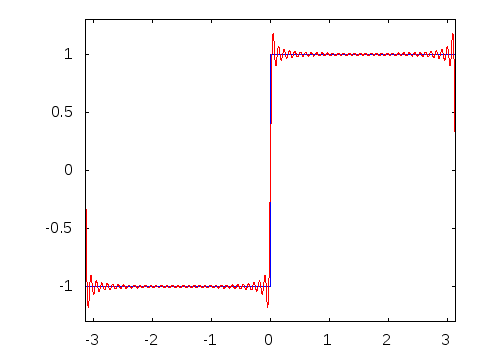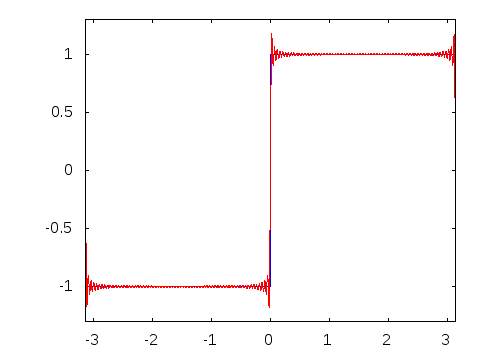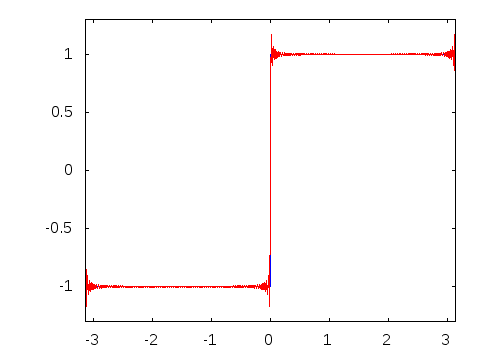 Square waves in physical systems have only finite bandwidth and often exhibit ringing effects similar to those of the Gibbs phenomenon or ripple effects similar to those of the σ-approximation.
For a reasonable approximation to the square-wave shape, at least the fundamental and third harmonic need to be present, with the fifth harmonic being desirable. These bandwidth requirements are important in digital electronics, where finite-bandwidth analog approximations to square-wave-like waveforms are used. (The ringing transients are an important electronic consideration here, as they may go beyond the electrical rating limits of a circuit or cause a badly positioned threshold to be crossed multiple times.)
Square waves in physical systems have only finite bandwidth and often exhibit ringing effects similar to those of the Gibbs phenomenon or ripple effects similar to those of the σ-approximation.
For a reasonable approximation to the square-wave shape, at least the fundamental and third harmonic need to be present, with the fifth harmonic being desirable. These bandwidth requirements are important in digital electronics, where finite-bandwidth analog approximations to square-wave-like waveforms are used. (The ringing transients are an important electronic consideration here, as they may go beyond the electrical rating limits of a circuit or cause a badly positioned threshold to be crossed multiple times.)
Fourier decomposition of a square wave
Interactive demo of square wave synthesis using sine waves, from GeoGebra site.
Square Wave Approximated by Sines
Interactive demo of square wave synthesis using sine waves.
Square wave. {{Waveforms Waveforms Fourier series
duty cycle
A duty cycle or power cycle is the fraction of one period in which a signal or system is active. Duty cycle is commonly expressed as a percentage or a ratio. A period is the time it takes for a signal to complete an on-and-off cycle. As a formu ...
. A true square wave has a 50% duty cycle (equal high and low periods).
Square waves are often encountered in electronics and signal processing, particularly digital electronics and digital signal processing
Digital signal processing (DSP) is the use of digital processing, such as by computers or more specialized digital signal processors, to perform a wide variety of signal processing operations. The digital signals processed in this manner are ...
. Its stochastic
Stochastic (, ) refers to the property of being well described by a random probability distribution. Although stochasticity and randomness are distinct in that the former refers to a modeling approach and the latter refers to phenomena themselv ...
counterpart is a two-state trajectory.
Origin and uses
Square waves are universally encountered indigital
Digital usually refers to something using discrete digits, often binary digits.
Technology and computing Hardware
*Digital electronics, electronic circuits which operate using digital signals
**Digital camera, which captures and stores digital i ...
switching circuits and are naturally generated by binary (two-level) logic devices. Square waves are typically generated by metal–oxide–semiconductor field-effect transistor (MOSFET) devices due to their rapid on–off electronic switching behavior, in contrast to bipolar junction transistors (BJTs) which slowly generate signals more closely resembling sine waves rather than square waves.
Square waves are used as timing references or "clock signal
In electronics and especially synchronous digital circuits, a clock signal (historically also known as ''logic beat'') oscillates between a high and a low state and is used like a metronome to coordinate actions of digital circuits.
A clock sign ...
s", because their fast transitions are suitable for triggering synchronous logic
In digital electronics, a synchronous circuit is a digital circuit in which the changes in the state of memory elements are synchronized by a clock signal. In a sequential digital logic circuit, data are stored in memory devices called flip-fl ...
circuits at precisely determined intervals. However, as the frequency-domain graph shows, square waves contain a wide range of harmonics; these can generate electromagnetic radiation or pulses of current that interfere with other nearby circuits, causing noise or errors. To avoid this problem in very sensitive circuits such as precision analog-to-digital converters, sine wave
A sine wave, sinusoidal wave, or just sinusoid is a curve, mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph of a function, graph. It is a type of continuous wave and also a Smoothness, smooth p ...
s are used instead of square waves as timing references.
In musical terms, they are often described as sounding hollow, and are therefore used as the basis for wind instrument sounds created using subtractive synthesis. Additionally, the distortion effect used on electric guitars clips the outermost regions of the waveform, causing it to increasingly resemble a square wave as more distortion is applied.
Simple two-level Rademacher functions are square waves.
Definitions
The square wave in mathematics has many definitions, which are equivalent except at the discontinuities: It can be defined as simply thesign function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as . To avoi ...
of a sinusoid:
which will be 1 when the sinusoid is positive, −1 when the sinusoid is negative, and 0 at the discontinuities. Here, ''T'' is the period of the square wave and ''f'' is its frequency, which are related by the equation ''f'' = 1/''T''.
A square wave can also be defined with respect to the Heaviside step function ''u''(''t'') or the rectangular function Π(''t''):
A square wave can also be generated using the floor function directly:
and indirectly:
Fourier analysis

 Using Fourier expansion with cycle frequency over time , an ideal square wave with an amplitude of 1 can be represented as an infinite sum of sinusoidal waves:
The ideal square wave contains only components of odd-integer
Using Fourier expansion with cycle frequency over time , an ideal square wave with an amplitude of 1 can be represented as an infinite sum of sinusoidal waves:
The ideal square wave contains only components of odd-integer harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
frequencies (of the form ). Sawtooth waves and real-world signals contain all integer harmonics.
A curiosity of the convergence of the Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''p ...
representation of the square wave is the Gibbs phenomenon. Ringing artifacts
In signal processing, particularly digital image processing, ringing artifacts are artifacts that appear as spurious signals near sharp transitions in a signal. Visually, they appear as bands or "ghosts" near edges; audibly, they appear as "ec ...
in non-ideal square waves can be shown to be related to this phenomenon. The Gibbs phenomenon can be prevented by the use of σ-approximation, which uses the Lanczos sigma factors to help the sequence converge more smoothly.
An ideal mathematical square wave changes between the high and the low state instantaneously, and without under- or over-shooting. This is impossible to achieve in physical systems, as it would require infinite bandwidth.
 Square waves in physical systems have only finite bandwidth and often exhibit ringing effects similar to those of the Gibbs phenomenon or ripple effects similar to those of the σ-approximation.
For a reasonable approximation to the square-wave shape, at least the fundamental and third harmonic need to be present, with the fifth harmonic being desirable. These bandwidth requirements are important in digital electronics, where finite-bandwidth analog approximations to square-wave-like waveforms are used. (The ringing transients are an important electronic consideration here, as they may go beyond the electrical rating limits of a circuit or cause a badly positioned threshold to be crossed multiple times.)
Square waves in physical systems have only finite bandwidth and often exhibit ringing effects similar to those of the Gibbs phenomenon or ripple effects similar to those of the σ-approximation.
For a reasonable approximation to the square-wave shape, at least the fundamental and third harmonic need to be present, with the fifth harmonic being desirable. These bandwidth requirements are important in digital electronics, where finite-bandwidth analog approximations to square-wave-like waveforms are used. (The ringing transients are an important electronic consideration here, as they may go beyond the electrical rating limits of a circuit or cause a badly positioned threshold to be crossed multiple times.)
Characteristics of imperfect square waves
As already mentioned, an ideal square wave has instantaneous transitions between the high and low levels. In practice, this is never achieved because of physical limitations of the system that generates the waveform. The times taken for the signal to rise from the low level to the high level and back again are called the '' rise time'' and the '' fall time'' respectively. If the system is overdamped, then the waveform may never actually reach the theoretical high and low levels, and if the system is underdamped, it will oscillate about the high and low levels before settling down. In these cases, the rise and fall times are measured between specified intermediate levels, such as 5% and 95%, or 10% and 90%. The bandwidth of a system is related to the transition times of the waveform; there are formulas allowing one to be determined approximately from the other.See also
* List of periodic functions * Rectangular function * Pulse wave *Sine wave
A sine wave, sinusoidal wave, or just sinusoid is a curve, mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph of a function, graph. It is a type of continuous wave and also a Smoothness, smooth p ...
* Triangle wave
* Sawtooth wave
* Waveform
* Sound
* Multivibrator
* Ronchi ruling, a square-wave stripe target used in imaging.
* Cross sea
* Clarinet
The clarinet is a musical instrument in the woodwind family. The instrument has a nearly cylindrical bore and a flared bell, and uses a single reed to produce sound.
Clarinets comprise a family of instruments of differing sizes and pitches ...
, a musical instrument that produces odd overtones approximating a square wave.
References
External links
Fourier decomposition of a square wave
Interactive demo of square wave synthesis using sine waves, from GeoGebra site.
Square Wave Approximated by Sines
Interactive demo of square wave synthesis using sine waves.
Square wave. {{Waveforms Waveforms Fourier series