Specific Conductance on:
[Wikipedia]
[Google]
[Amazon]
Electrical resistivity (also called specific electrical resistance or volume resistivity) is a fundamental property of a material that measures how strongly it resists electric current. A low resistivity indicates a material that readily allows electric current. Resistivity is commonly represented by the
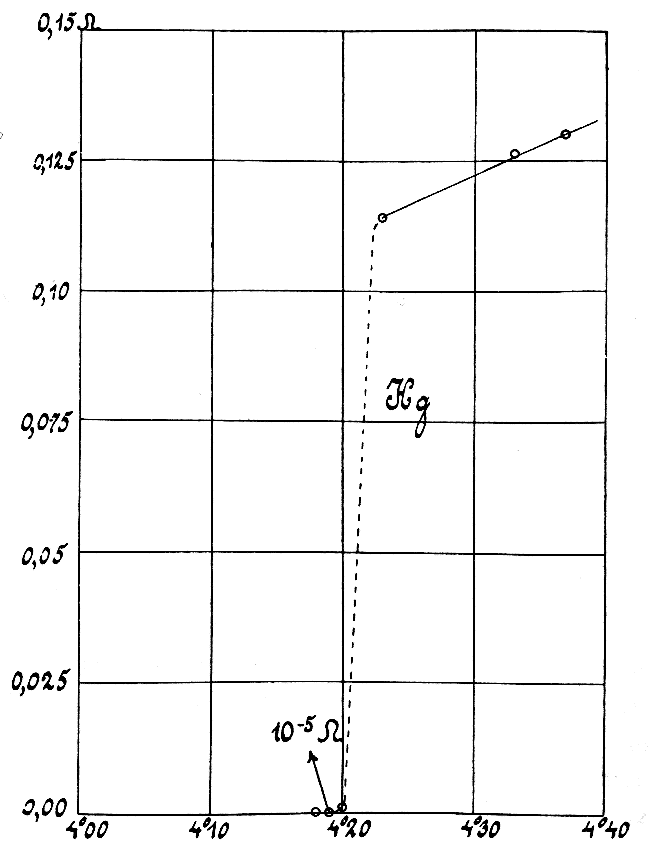 The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In normal (that is, non-superconducting) conductors, such as
The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In normal (that is, non-superconducting) conductors, such as
 Plasmas are very good conductors and electric potentials play an important role.
The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the ''plasma potential'', or ''space potential''. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a
Plasmas are very good conductors and electric potentials play an important role.
The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the ''plasma potential'', or ''space potential''. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a
Measuring Electrical Resistivity and Conductivity
Comparison of the electrical conductivity of various elements in WolframAlpha
* {{Authority control * Physical quantities Materials science
Greek letter
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BCE. It is derived from the earlier Phoenician alphabet, and was the earliest known alphabetic script to have distinct letters for vowels as ...
(rho
Rho (uppercase Ρ, lowercase ρ or ; el, ρο or el, ρω, label=none) is the 17th letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the sa ...
). The SI unit of electrical resistivity is the ohm
Ohm (symbol Ω) is a unit of electrical resistance named after Georg Ohm.
Ohm or OHM may also refer to:
People
* Georg Ohm (1789–1854), German physicist and namesake of the term ''ohm''
* Germán Ohm (born 1936), Mexican boxer
* Jörg Ohm (b ...
-meter
The metre (British spelling) or meter (American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its pref ...
(Ω⋅m). For example, if a solid cube of material has sheet contacts on two opposite faces, and the resistance between these contacts is , then the resistivity of the material is .
Electrical conductivity or specific conductance is the reciprocal of electrical resistivity. It represents a material's ability to conduct electric current. It is commonly signified by the Greek letter ( sigma), but ( kappa) (especially in electrical engineering) and ( gamma) are sometimes used. The SI unit of electrical conductivity is siemens
Siemens AG ( ) is a German multinational conglomerate corporation and the largest industrial manufacturing company in Europe headquartered in Munich with branch offices abroad.
The principal divisions of the corporation are ''Industry'', '' ...
per metre
The metre (British spelling) or meter (American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its pref ...
(S/m). Resistivity and conductivity are intensive properties
Physical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes. According to IUPAC, an intensive quantity is one ...
of materials, giving the opposition of a standard cube of material to current. Electrical resistance and conductance are corresponding extensive properties
Physical properties of materials and systems can often be categorized as being either intensive or extensive, according to how the property changes when the size (or extent) of the system changes. According to IUPAC, an intensive quantity is one ...
that give the opposition of a specific object to electric current.
Definition
Ideal case
In an ideal case, cross-section and physical composition of the examined material are uniform across the sample, and the electric field and current density are both parallel and constant everywhere. Many resistors and conductors do in fact have a uniform cross section with a uniform flow of electric current, and are made of a single material, so that this is a good model. (See the adjacent diagram.) When this is the case, the electrical resistivity (Greek:rho
Rho (uppercase Ρ, lowercase ρ or ; el, ρο or el, ρω, label=none) is the 17th letter of the Greek alphabet. In the system of Greek numerals it has a value of 100. It is derived from Phoenician letter res . Its uppercase form uses the sa ...
) can be calculated by:
where
The resistivity can be expressed using the SI unit ohm
Ohm (symbol Ω) is a unit of electrical resistance named after Georg Ohm.
Ohm or OHM may also refer to:
People
* Georg Ohm (1789–1854), German physicist and namesake of the term ''ohm''
* Germán Ohm (born 1936), Mexican boxer
* Jörg Ohm (b ...
metre
The metre (British spelling) or meter (American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its pref ...
(Ω⋅m) — ''i.e.'' ohms multiplied by square metres (for the cross-sectional area) then divided by metres (for the length).
Both ''resistance'' and ''resistivity'' describe how difficult it is to make electrical current flow through a material, but unlike resistance, resistivity is an intrinsic property
In science and engineering, an intrinsic property is a property of a specified subject that exists itself or within the subject. An extrinsic property is not essential or inherent to the subject that is being characterized. For example, mass ...
. This means that all pure copper wires (which have not been subjected to distortion of their crystalline structure etc.), irrespective of their shape and size, have the same resistivity, but a long, thin copper wire has a much larger resistance than a thick, short copper wire. Every material has its own characteristic resistivity. For example, rubber has a far larger resistivity than copper.
In a hydraulic analogy
The electronic–hydraulic analogy (derisively referred to as the drain-pipe theory by Oliver Lodge) is the most widely used analogy for "electron fluid" in a metal conductor. Since electric current is invisible and the processes in play in ...
, passing current through a high-resistivity material is like pushing water through a pipe full of sand - while passing current through a low-resistivity material is like pushing water through an empty pipe. If the pipes are the same size and shape, the pipe full of sand has higher resistance to flow. Resistance, however, is not ''solely'' determined by the presence or absence of sand. It also depends on the length and width of the pipe: short or wide pipes have lower resistance than narrow or long pipes.
The above equation can be transposed to get Pouillet's law (named after Claude Pouillet
Claude Servais Mathias Pouillet (16 February 1790 – 14 June 1868) was a French physicist and a professor of physics at the Sorbonne and member of the French Academy of Sciences (elected 1837).
Biography
He studied sciences at the École n ...
):
The resistance of a given element is proportional to the length, but inversely proportional to the cross-sectional area. For example, if = , = (forming a cube with perfectly conductive contacts on opposite faces), then the resistance of this element in ohms is numerically equal to the resistivity of the material it is made of in Ω⋅m.
Conductivity, , is the inverse of resistivity:
Conductivity has SI units of siemens
Siemens AG ( ) is a German multinational conglomerate corporation and the largest industrial manufacturing company in Europe headquartered in Munich with branch offices abroad.
The principal divisions of the corporation are ''Industry'', '' ...
per metre (S/m).
General scalar quantities
For less ideal cases, such as more complicated geometry, or when the current and electric field vary in different parts of the material, it is necessary to use a more general expression in which the resistivity at a particular point is defined as the ratio of the electric field to thedensity
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
of the current it creates at that point:
where
in which and are inside the conductor.
Conductivity is the inverse (reciprocal) of resistivity. Here, it is given by:
For example, rubber is a material with large and small — because even a very large electric field in rubber makes almost no current flow through it. On the other hand, copper is a material with small and large — because even a small electric field pulls a lot of current through it.
As shown below, this expression simplifies to a single number when the electric field and current density are constant in the material.
:
Tensor resistivity
When the resistivity of a material has a directional component, the most general definition of resistivity must be used. It starts from the tensor-vector form of Ohm's law, which relates the electric field inside a material to the electric current flow. This equation is completely general, meaning it is valid in all cases, including those mentioned above. However, this definition is the most complicated, so it is only directly used in anisotropic cases, where the more simple definitions cannot be applied. If the material is not anisotropic, it is safe to ignore the tensor-vector definition, and use a simpler expression instead. Here, anisotropic means that the material has different properties in different directions. For example, a crystal ofgraphite
Graphite () is a crystalline form of the element carbon. It consists of stacked layers of graphene. Graphite occurs naturally and is the most stable form of carbon under standard conditions. Synthetic and natural graphite are consumed on lar ...
consists microscopically of a stack of sheets, and current flows very easily through each sheet, but much less easily from one sheet to the adjacent one. In such cases, the current does not flow in exactly the same direction as the electric field. Thus, the appropriate equations are generalized to the three-dimensional tensor form:
where the conductivity and resistivity are rank-2 tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensor ...
s, and electric field and current density are vectors. These tensors can be represented by 3×3 matrices, the vectors with 3×1 matrices, with matrix multiplication
In mathematics, particularly in linear algebra, matrix multiplication is a binary operation that produces a matrix from two matrices. For matrix multiplication, the number of columns in the first matrix must be equal to the number of rows in the s ...
used on the right side of these equations. In matrix form, the resistivity relation is given by:
where
Equivalently, resistivity can be given in the more compact Einstein notation:
In either case, the resulting expression for each electric field component is:
Since the choice of the coordinate system is free, the usual convention is to simplify the expression by choosing an -axis parallel to the current direction, so . This leaves:
Conductivity is defined similarly:
or
both resulting in:
Looking at the two expressions, and are the matrix inverse
In linear algebra, an -by- square matrix is called invertible (also nonsingular or nondegenerate), if there exists an -by- square matrix such that
:\mathbf = \mathbf = \mathbf_n \
where denotes the -by- identity matrix and the multiplica ...
of each other. However, in the most general case, the individual matrix elements are not necessarily reciprocals of one another; for example, may not be equal to . This can be seen in the Hall effect
The Hall effect is the production of a voltage difference (the Hall voltage) across an electrical conductor that is transverse to an electric current in the conductor and to an applied magnetic field perpendicular to the current. It was dis ...
, where is nonzero. In the Hall effect, due to rotational invariance about the -axis, and , so the relation between resistivity and conductivity simplifies to:
If the electric field is parallel to the applied current, and are zero. When they are zero, one number, , is enough to describe the electrical resistivity. It is then written as simply , and this reduces to the simpler expression.
Conductivity and current carriers
Relation between current density and electric current velocity
Electric current is the ordered movement ofelectric charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respe ...
s.
Causes of conductivity
Band theory simplified
According to elementaryquantum mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, ...
, an electron in an atom or crystal can only have certain precise energy levels; energies between these levels are impossible. When a large number of such allowed levels have close-spaced energy values – i.e. have energies that differ only minutely – those close energy levels in combination are called an "energy band". There can be many such energy bands in a material, depending on the atomic number of the constituent atomsThe atomic number is the count of electrons in an atom that is electrically neutral – has no net electric charge. and their distribution within the crystal.Other relevant factors that are specifically not considered are the size of the whole crystal and external factors of the surrounding environment that modify the energy bands, such as imposed electric or magnetic fields.
The material's electrons seek to minimize the total energy in the material by settling into low energy states; however, the Pauli exclusion principle
In quantum mechanics, the Pauli exclusion principle states that two or more identical particles with half-integer spins (i.e. fermions) cannot occupy the same quantum state within a quantum system simultaneously. This principle was formulat ...
means that only one can exist in each such state. So the electrons "fill up" the band structure starting from the bottom. The characteristic energy level up to which the electrons have filled is called the Fermi level. The position of the Fermi level with respect to the band structure is very important for electrical conduction: Only electrons in energy levels near or above the Fermi level are free to move within the broader material structure, since the electrons can easily jump among the partially occupied states in that region. In contrast, the low energy states are completely filled with a fixed limit on the number of electrons at all times, and the high energy states are empty of electrons at all times.
Electric current consists of a flow of electrons. In metals there are many electron energy levels near the Fermi level, so there are many electrons available to move. This is what causes the high electronic conductivity of metals.
An important part of band theory is that there may be forbidden bands of energy: energy intervals that contain no energy levels. In insulators and semiconductors, the number of electrons is just the right amount to fill a certain integer number of low energy bands, exactly to the boundary. In this case, the Fermi level falls within a band gap. Since there are no available states near the Fermi level, and the electrons are not freely movable, the electronic conductivity is very low.
In metals
Ametal
A metal (from Greek μέταλλον ''métallon'', "mine, quarry, metal") is a material that, when freshly prepared, polished, or fractured, shows a lustrous appearance, and conducts electricity and heat relatively well. Metals are typicall ...
consists of a lattice
Lattice may refer to:
Arts and design
* Latticework, an ornamental criss-crossed framework, an arrangement of crossing laths or other thin strips of material
* Lattice (music), an organized grid model of pitch ratios
* Lattice (pastry), an orna ...
of atom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas, ...
s, each with an outer shell of electrons that freely dissociate from their parent atoms and travel through the lattice. This is also known as a positive ionic lattice. This 'sea' of dissociable electrons allows the metal to conduct electric current. When an electrical potential difference (a voltage
Voltage, also known as electric pressure, electric tension, or (electric) potential difference, is the difference in electric potential between two points. In a static electric field, it corresponds to the work needed per unit of charge to m ...
) is applied across the metal, the resulting electric field causes electrons to drift towards the positive terminal. The actual drift velocity of electrons is typically small, on the order of magnitude of meters per hour. However, due to the sheer number of moving electrons, even a slow drift velocity results in a large current density. The mechanism is similar to transfer of momentum of balls in a Newton's cradle
The Newton's cradle is a device that demonstrates the conservation of momentum and the conservation of energy with swinging spheres. When one sphere at the end is lifted and released, it strikes the stationary spheres, transmitting a force thro ...
but the rapid propagation of an electric energy along a wire is not due to the mechanical forces, but the propagation of an energy-carrying electromagnetic field guided by the wire.
Most metals have electrical resistance. In simpler models (non quantum mechanical models) this can be explained by replacing electrons and the crystal lattice by a wave-like structure. When the electron wave travels through the lattice, the waves interfere, which causes resistance. The more regular the lattice is, the less disturbance happens and thus the less resistance. The amount of resistance is thus mainly caused by two factors. First, it is caused by the temperature and thus amount of vibration of the crystal lattice. Higher temperatures cause bigger vibrations, which act as irregularities in the lattice. Second, the purity of the metal is relevant as a mixture of different ions is also an irregularity. The small decrease in conductivity on melting of pure metals is due to the loss of long range crystalline order. The short range order remains and strong correlation between positions of ions results in coherence between waves diffracted by adjacent ions.
In semiconductors and insulators
In metals, the Fermi level lies in the conduction band (see Band Theory, above) giving rise to free conduction electrons. However, in semiconductors the position of the Fermi level is within the band gap, about halfway between the conduction band minimum (the bottom of the first band of unfilled electron energy levels) and the valence band maximum (the top of the band below the conduction band, of filled electron energy levels). That applies for intrinsic (undoped) semiconductors. This means that at absolute zero temperature, there would be no free conduction electrons, and the resistance is infinite. However, the resistance decreases as the charge carrier density (i.e., without introducing further complications, the density of electrons) in the conduction band increases. In extrinsic (doped) semiconductors,dopant
A dopant, also called a doping agent, is a trace of impurity element that is introduced into a chemical material to alter its original electrical or optical properties. The amount of dopant necessary to cause changes is typically very low. When ...
atoms increase the majority charge carrier concentration by donating electrons to the conduction band or producing holes in the valence band. (A "hole" is a position where an electron is missing; such holes can behave in a similar way to electrons.) For both types of donor or acceptor atoms, increasing dopant density reduces resistance. Hence, highly doped semiconductors behave metallically. At very high temperatures, the contribution of thermally generated carriers dominates over the contribution from dopant atoms, and the resistance decreases exponentially with temperature.
In ionic liquids/electrolytes
In electrolytes, electrical conduction happens not by band electrons or holes, but by full atomic species (ion
An ion () is an atom or molecule with a net electrical charge.
The charge of an electron is considered to be negative by convention and this charge is equal and opposite to the charge of a proton, which is considered to be positive by conve ...
s) traveling, each carrying an electrical charge. The resistivity of ionic solutions (electrolytes) varies tremendously with concentration – while distilled water is almost an insulator, salt water
Saline water (more commonly known as salt water) is water that contains a high concentration of dissolved salts (mainly sodium chloride). On the United States Geological Survey (USGS) salinity scale, saline water is saltier than brackish wat ...
is a reasonable electrical conductor. Conduction in ionic liquid
An ionic liquid (IL) is a salt in the liquid state. In some contexts, the term has been restricted to salts whose melting point is below a specific temperature, such as . While ordinary liquids such as water and gasoline are predominantly made of ...
s is also controlled by the movement of ions, but here we are talking about molten salts rather than solvated ions. In biological membranes
A biological membrane, biomembrane or cell membrane is a selectively permeable membrane that separates the interior of a cell from the external environment or creates intracellular compartments by serving as a boundary between one part of the c ...
, currents are carried by ionic salts. Small holes in cell membranes, called ion channel
Ion channels are pore-forming membrane proteins that allow ions to pass through the channel pore. Their functions include establishing a resting membrane potential, shaping action potentials and other electrical signals by gating the flow of io ...
s, are selective to specific ions and determine the membrane resistance.
The concentration of ions in a liquid (''e.g.'', in an aqueous solution) depends on the degree of dissociation of the dissolved substance, characterized by a dissociation coefficient , which is the ratio of the concentration of ions to the concentration of molecules of the dissolved substance :
The specific electrical conductivity () of a solution is equal to:
where : module of the ion charge, and : mobility of positively and negatively charged ions, : concentration of molecules of the dissolved substance, : the coefficient of dissociation.
Superconductivity
 The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In normal (that is, non-superconducting) conductors, such as
The electrical resistivity of a metallic conductor decreases gradually as temperature is lowered. In normal (that is, non-superconducting) conductors, such as copper
Copper is a chemical element with the symbol Cu (from la, cuprum) and atomic number 29. It is a soft, malleable, and ductile metal with very high thermal and electrical conductivity. A freshly exposed surface of pure copper has a pinkis ...
or silver
Silver is a chemical element with the Symbol (chemistry), symbol Ag (from the Latin ', derived from the Proto-Indo-European wikt:Reconstruction:Proto-Indo-European/h₂erǵ-, ''h₂erǵ'': "shiny" or "white") and atomic number 47. A soft, whi ...
, this decrease is limited by impurities and other defects. Even near absolute zero, a real sample of a normal conductor shows some resistance. In a superconductor, the resistance drops abruptly to zero when the material is cooled below its critical temperature. In a normal conductor, the current is driven by a voltage gradient, whereas in a superconductor, there is no voltage gradient and the current is instead related to the phase gradient of the superconducting order parameter. A consequence of this is that an electric current flowing in a loop of superconducting wire can persist indefinitely with no power source.
In a class of superconductors known as type II superconductor
In superconductivity, a type-II superconductor is a superconductor that exhibits an intermediate phase of mixed ordinary and superconducting properties at intermediate temperature and fields above the superconducting phases.
It also features the ...
s, including all known high-temperature superconductor
High-temperature superconductors (abbreviated high-c or HTS) are defined as materials that behave as superconductors at temperatures above , the boiling point of liquid nitrogen. The adjective "high temperature" is only in respect to previou ...
s, an extremely low but nonzero resistivity appears at temperatures not too far below the nominal superconducting transition when an electric current is applied in conjunction with a strong magnetic field, which may be caused by the electric current. This is due to the motion of magnetic vortices in the electronic superfluid, which dissipates some of the energy carried by the current. The resistance due to this effect is tiny compared with that of non-superconducting materials, but must be taken into account in sensitive experiments. However, as the temperature decreases far enough below the nominal superconducting transition, these vortices can become frozen so that the resistance of the material becomes truly zero.
Plasma
 Plasmas are very good conductors and electric potentials play an important role.
The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the ''plasma potential'', or ''space potential''. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a
Plasmas are very good conductors and electric potentials play an important role.
The potential as it exists on average in the space between charged particles, independent of the question of how it can be measured, is called the ''plasma potential'', or ''space potential''. If an electrode is inserted into a plasma, its potential generally lies considerably below the plasma potential, due to what is termed a Debye sheath The Debye sheath (also electrostatic sheath) is a layer in a plasma which has a greater density of positive ions, and hence an overall excess positive charge, that balances an opposite negative charge on the surface of a material with which it is i ...
. The good electrical conductivity of plasmas makes their electric fields very small. This results in the important concept of ''quasineutrality'', which says the density of negative charges is approximately equal to the density of positive charges over large volumes of the plasma (), but on the scale of the Debye length
In plasmas and electrolytes, the Debye length \lambda_ (also called Debye radius), is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are in ...
there can be charge imbalance. In the special case that '' double layers'' are formed, the charge separation can extend some tens of Debye lengths.
The magnitude of the potentials and electric fields must be determined by means other than simply finding the net charge density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in ...
. A common example is to assume that the electrons satisfy the Boltzmann relation
In a plasma, the Boltzmann relation describes the number density of an isothermal charged particle fluid when the thermal and the electrostatic forces acting on the fluid have reached equilibrium.
In many situations, the electron density of a ...
:
Differentiating this relation provides a means to calculate the electric field from the density:
(∇ is the vector gradient operator; see nabla symbol
The nabla symbol
The nabla is a triangular symbol resembling an inverted Greek delta:Indeed, it is called ( ανάδελτα) in Modern Greek. \nabla or ∇. The name comes, by reason of the symbol's shape, from the Hellenistic Greek word ...
and gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
for more information.)
It is possible to produce a plasma that is not quasineutral. An electron beam, for example, has only negative charges. The density of a non-neutral plasma must generally be very low, or it must be very small. Otherwise, the repulsive electrostatic force
Coulomb's inverse-square law, or simply Coulomb's law, is an experimental law of physics that quantifies the amount of force between two stationary, electrically charged particles. The electric force between charged bodies at rest is convention ...
dissipates it.
In astrophysical
Astrophysics is a science that employs the methods and principles of physics and chemistry in the study of astronomical objects and phenomena. As one of the founders of the discipline said, Astrophysics "seeks to ascertain the nature of the h ...
plasmas, Debye screening prevents electric fields from directly affecting the plasma over large distances, i.e., greater than the Debye length
In plasmas and electrolytes, the Debye length \lambda_ (also called Debye radius), is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are in ...
. However, the existence of charged particles causes the plasma to generate, and be affected by, magnetic fields. This can and does cause extremely complex behavior, such as the generation of plasma double layers, an object that separates charge over a few tens of Debye length
In plasmas and electrolytes, the Debye length \lambda_ (also called Debye radius), is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are in ...
s. The dynamics of plasmas interacting with external and self-generated magnetic fields are studied in the academic discipline of magnetohydrodynamics
Magnetohydrodynamics (MHD; also called magneto-fluid dynamics or hydromagnetics) is the study of the magnetic properties and behaviour of electrically conducting fluids. Examples of such magnetofluids include plasmas, liquid metals, ...
.
Plasma is often called the ''fourth state of matter
In physics, a state of matter is one of the distinct forms in which matter can exist. Four states of matter are observable in everyday life: solid, liquid, gas, and plasma. Many intermediate states are known to exist, such as liquid crystal ...
'' after solid, liquids and gases. It is distinct from these and other lower-energy states of matter
In physics, a state of matter is one of the distinct forms in which matter can exist. Four states of matter are observable in everyday life: solid, liquid, gas, and plasma. Many intermediate states are known to exist, such as liquid crystal, ...
. Although it is closely related to the gas phase in that it also has no definite form or volume, it differs in a number of ways, including the following:
Resistivity and conductivity of various materials
* A conductor such as a metal has high conductivity and a low resistivity. * An insulator likeglass
Glass is a non-crystalline, often transparent, amorphous solid that has widespread practical, technological, and decorative use in, for example, window panes, tableware, and optics. Glass is most often formed by rapid cooling ( quenching ...
has low conductivity and a high resistivity.
* The conductivity of a semiconductor
A semiconductor is a material which has an electrical resistivity and conductivity, electrical conductivity value falling between that of a electrical conductor, conductor, such as copper, and an insulator (electricity), insulator, such as glas ...
is generally intermediate, but varies widely under different conditions, such as exposure of the material to electric fields or specific frequencies of light
Light or visible light is electromagnetic radiation that can be perceived by the human eye. Visible light is usually defined as having wavelengths in the range of 400–700 nanometres (nm), corresponding to frequencies of 750–420 te ...
, and, most important, with temperature
Temperature is a physical quantity that expresses quantitatively the perceptions of hotness and coldness. Temperature is measurement, measured with a thermometer.
Thermometers are calibrated in various Conversion of units of temperature, temp ...
and composition of the semiconductor material.
The degree of semiconductors doping makes a large difference in conductivity. To a point, more doping leads to higher conductivity. The conductivity of a water
Water (chemical formula ) is an inorganic, transparent, tasteless, odorless, and nearly colorless chemical substance, which is the main constituent of Earth's hydrosphere and the fluids of all known living organisms (in which it acts as a ...
/aqueous
An aqueous solution is a solution in which the solvent is water. It is mostly shown in chemical equations by appending (aq) to the relevant chemical formula. For example, a solution of table salt, or sodium chloride (NaCl), in water would be re ...
solution
Solution may refer to:
* Solution (chemistry), a mixture where one substance is dissolved in another
* Solution (equation), in mathematics
** Numerical solution, in numerical analysis, approximate solutions within specified error bounds
* Soluti ...
is highly dependent on its concentration
In chemistry, concentration is the abundance of a constituent divided by the total volume of a mixture. Several types of mathematical description can be distinguished: '' mass concentration'', ''molar concentration'', '' number concentration'', ...
of dissolved salts
In chemistry, a salt is a chemical compound consisting of an ionic assembly of positively charged cations and negatively charged anions, which results in a compound with no net electric charge. A common example is table salt, with positively c ...
, and other chemical species that ionize
Ionization, or Ionisation is the process by which an atom or a molecule acquires a negative or positive charge by gaining or losing electrons, often in conjunction with other chemical changes. The resulting electrically charged atom or molecule ...
in the solution. Electrical conductivity of water samples is used as an indicator of how salt-free, ion-free, or impurity-free the sample is; the purer the water, the lower the conductivity (the higher the resistivity). Conductivity measurements in water are often reported as ''specific conductance'', relative to the conductivity of pure water at . An EC meter
An electrical conductivity meter (EC meter) measures the electrical conductivity in a solution. It has multiple applications in research and engineering, with common usage in hydroponics, aquaculture, aquaponics, and freshwater systems to m ...
is normally used to measure conductivity in a solution. A rough summary is as follows:
This table shows the resistivity (), conductivity and temperature coefficient
A temperature coefficient describes the relative change of a physical property that is associated with a given change in temperature. For a property ''R'' that changes when the temperature changes by ''dT'', the temperature coefficient α is def ...
of various materials at .
The effective temperature coefficient varies with temperature and purity level of the material. The 20 °C value is only an approximation when used at other temperatures. For example, the coefficient becomes lower at higher temperatures for copper, and the value 0.00427 is commonly specified at .
The extremely low resistivity (high conductivity) of silver is characteristic of metals. George Gamow
George Gamow (March 4, 1904 – August 19, 1968), born Georgiy Antonovich Gamov ( uk, Георгій Антонович Гамов, russian: Георгий Антонович Гамов), was a Russian-born Soviet and American polymath, theoret ...
tidily summed up the nature of the metals' dealings with electrons in his popular science book ''One, Two, Three...Infinity'' (1947):
More technically, the free electron model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quantu ...
gives a basic description of electron flow in metals.
Wood is widely regarded as an extremely good insulator, but its resistivity is sensitively dependent on moisture content, with damp wood being a factor of at least worse insulator than oven-dry. In any case, a sufficiently high voltage – such as that in lightning strikes or some high-tension power lines – can lead to insulation breakdown and electrocution risk even with apparently dry wood.
Temperature dependence
Linear approximation
The electrical resistivity of most materials changes with temperature. If the temperature does not vary too much, alinear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). They are widely used in the method of finite differences to produce first order methods for solving o ...
is typically used:
where is called the ''temperature coefficient
A temperature coefficient describes the relative change of a physical property that is associated with a given change in temperature. For a property ''R'' that changes when the temperature changes by ''dT'', the temperature coefficient α is def ...
of resistivity'', is a fixed reference temperature (usually room temperature), and is the resistivity at temperature . The parameter is an empirical parameter fitted from measurement data. Because the linear approximation is only an approximation, is different for different reference temperatures. For this reason it is usual to specify the temperature that was measured at with a suffix, such as , and the relationship only holds in a range of temperatures around the reference. When the temperature varies over a large temperature range, the linear approximation
In mathematics, a linear approximation is an approximation of a general function using a linear function (more precisely, an affine function). They are widely used in the method of finite differences to produce first order methods for solving o ...
is inadequate and a more detailed analysis and understanding should be used.
Metals
In general, electrical resistivity of metals increases with temperature. Electron– phonon interactions can play a key role. At high temperatures, the resistance of a metal increases linearly with temperature. As the temperature of a metal is reduced, the temperature dependence of resistivity follows a power law function of temperature. Mathematically the temperature dependence of the resistivity of a metal can be approximated through the Bloch–Grüneisen formula: where is the residual resistivity due to defect scattering, A is a constant that depends on the velocity of electrons at theFermi surface In condensed matter physics, the Fermi surface is the surface in reciprocal space which separates occupied from unoccupied electron states at zero temperature. The shape of the Fermi surface is derived from the periodicity and symmetry of the crys ...
, the Debye radius
In plasmas and electrolytes, the Debye length \lambda_ (also called Debye radius), is a measure of a charge carrier's net electrostatic effect in a solution and how far its electrostatic effect persists. With each Debye length the charges are i ...
and the number density of electrons in the metal. is the Debye temperature
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat (Heat capacity) in a solid. It treats the vibrations of the atomic lattice (hea ...
as obtained from resistivity measurements and matches very closely with the values of Debye temperature obtained from specific heat measurements. n is an integer that depends upon the nature of interaction:
* = 5 implies that the resistance is due to scattering of electrons by phonons (as it is for simple metals)
* = 3 implies that the resistance is due to s-d electron scattering (as is the case for transition metals)
* = 2 implies that the resistance is due to electron–electron interaction.
The Bloch–Grüneisen formula is an approximation obtained assuming that the studied metal has spherical Fermi surface inscribed within the first Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. In the same way the Bravais lattice is divided up into Wigner–Seitz cells in the real lattice, the reciprocal lattice ...
and a Debye phonon spectrum.
If more than one source of scattering is simultaneously present, Matthiessen's rule (first formulated by Augustus Matthiessen
Augustus Matthiessen, FRS (2 January 1831, in London – 6 October 1870, in London), the son of a merchant, was a British chemist and physicist who obtained his PhD in Germany at the University of Gießen in 1852 with Johann Heinrich Buff. He ...
in the 1860s) states that the total resistance can be approximated by adding up several different terms, each with the appropriate value of .
As the temperature of the metal is sufficiently reduced (so as to 'freeze' all the phonons), the resistivity usually reaches a constant value, known as the residual resistivity. This value depends not only on the type of metal, but on its purity and thermal history. The value of the residual resistivity of a metal is decided by its impurity concentration. Some materials lose all electrical resistivity at sufficiently low temperatures, due to an effect known as superconductivity.
An investigation of the low-temperature resistivity of metals was the motivation to Heike Kamerlingh Onnes
Heike Kamerlingh Onnes (21 September 1853 – 21 February 1926) was a Dutch physicist and Nobel laureate. He exploited the Hampson–Linde cycle to investigate how materials behave when cooled to nearly absolute zero and later to liquefy heliu ...
's experiments that led in 1911 to discovery of superconductivity. For details see History of superconductivity Superconductivity is the phenomenon of certain materials exhibiting zero electrical resistance and the expulsion of magnetic fields below a characteristic temperature. The history of superconductivity began with Dutch physicist Heike Kamerlingh Onne ...
.
Wiedemann–Franz law
TheWiedemann–Franz law In physics, the Wiedemann–Franz law states that the ratio of the electronic contribution of the thermal conductivity (''κ'') to the electrical conductivity (''σ'') of a metal is proportional to the temperature (''T'').
: \frac \kapp ...
states that the coefficient of electrical conductivity of metals at normal temperatures is inversely proportional to the temperature:
For metals at high temperatures, the Wiedemann–Franz law holds:
where is the thermal conductivity
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by k, \lambda, or \kappa.
Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal ...
of the metal, is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative kinetic energy of particles in a gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin and the gas constant, ...
, is the electron charge, is temperature, and is the electrical conductivity coefficient.
Semiconductors
In general,intrinsic semiconductor
An intrinsic (pure) semiconductor, also called an undoped semiconductor or i-type semiconductor, is a pure semiconductor without any significant dopant species present. The number of charge carriers is therefore determined by the properties of the ...
resistivity decreases with increasing temperature. The electrons are bumped to the conduction energy band by thermal energy, where they flow freely, and in doing so leave behind holes
A hole is an opening in or through a particular medium, usually a solid body. Holes occur through natural and artificial processes, and may be useful for various purposes, or may represent a problem needing to be addressed in many fields of en ...
in the valence band
In solid-state physics, the valence band and conduction band are the bands closest to the Fermi level, and thus determine the electrical conductivity of the solid. In nonmetals, the valence band is the highest range of electron energies in w ...
, which also flow freely. The electric resistance of a typical intrinsic
In science and engineering, an intrinsic property is a property of a specified subject that exists itself or within the subject. An extrinsic property is not essential or inherent to the subject that is being characterized. For example, mass ...
(non doped) semiconductor
A semiconductor is a material which has an electrical resistivity and conductivity, electrical conductivity value falling between that of a electrical conductor, conductor, such as copper, and an insulator (electricity), insulator, such as glas ...
decreases exponentially
Exponential may refer to any of several mathematical topics related to exponentiation, including:
*Exponential function, also:
**Matrix exponential, the matrix analogue to the above
*Exponential decay, decrease at a rate proportional to value
*Expo ...
with temperature:
An even better approximation of the temperature dependence of the resistivity of a semiconductor is given by the Steinhart–Hart equation:
where , and are the so-called Steinhart–Hart coefficients.
This equation is used to calibrate thermistor
A thermistor is a type of resistor whose resistance is strongly dependent on temperature, more so than in standard resistors. The word thermistor is a portmanteau of ''thermal'' and ''resistor''.
Thermistors are divided based on their conduction ...
s.
Extrinsic (doped) semiconductors have a far more complicated temperature profile. As temperature increases starting from absolute zero they first decrease steeply in resistance as the carriers leave the donors or acceptors. After most of the donors or acceptors have lost their carriers, the resistance starts to increase again slightly due to the reducing mobility of carriers (much as in a metal). At higher temperatures, they behave like intrinsic semiconductors as the carriers from the donors/acceptors become insignificant compared to the thermally generated carriers.
In non-crystalline semiconductors, conduction can occur by charges quantum tunnelling from one localised site to another. This is known as variable range hopping Variable-range hopping is a model used to describe carrier transport in a disordered semiconductor or in amorphous solid by hopping in an extended temperature range. It has a characteristic temperature dependence of
:\sigma= \sigma_0e^
where \sigm ...
and has the characteristic form of
where = 2, 3, 4, depending on the dimensionality of the system.
Complex resistivity and conductivity
When analyzing the response of materials to alternating electric fields (dielectric spectroscopy
Dielectric spectroscopy (which falls in a subcategory of impedance spectroscopy) measures the dielectric properties of a medium as a function of frequency.Kremer F., Schonhals A., Luck W. Broadband Dielectric Spectroscopy. – Springer-Verlag, 200 ...
), in applications such as electrical impedance tomography
Electrical impedance tomography (EIT) is a noninvasive type of medical imaging in which the electrical conductivity, permittivity, and impedance of a part of the body is inferred from surface electrode measurements and used to form a tomographic ...
, it is convenient to replace resistivity with a complex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
quantity called impedivity (in analogy to electrical impedance
In electrical engineering, impedance is the opposition to alternating current presented by the combined effect of resistance and reactance in a circuit.
Quantitatively, the impedance of a two-terminal circuit element is the ratio of the com ...
). Impedivity is the sum of a real component, the resistivity, and an imaginary component, the reactivity (in analogy to reactance). The magnitude of impedivity is the square root of sum of squares of magnitudes of resistivity and reactivity.
Conversely, in such cases the conductivity must be expressed as a complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
(or even as a matrix of complex numbers, in the case of anisotropic materials) called the '' admittivity''. Admittivity is the sum of a real component called the conductivity and an imaginary component called the susceptivity.
An alternative description of the response to alternating currents uses a real (but frequency-dependent) conductivity, along with a real permittivity
In electromagnetism, the absolute permittivity, often simply called permittivity and denoted by the Greek letter ''ε'' (epsilon), is a measure of the electric polarizability of a dielectric. A material with high permittivity polarizes more in ...
. The larger the conductivity is, the more quickly the alternating-current signal is absorbed by the material (i.e., the more opaque
Opacity or opaque may refer to:
* Impediments to (especially, visible) light:
** Opacities, absorption coefficients
** Opacity (optics), property or degree of blocking the transmission of light
* Metaphors derived from literal optics:
** In lingu ...
the material is). For details, see Mathematical descriptions of opacity When an electromagnetic wave travels through a medium in which it gets attenuated (this is called an "opaque" or " attenuating" medium), it undergoes exponential decay as described by the Beer–Lambert law. However, there are many possible ways to ...
.
Resistance versus resistivity in complicated geometries
Even if the material's resistivity is known, calculating the resistance of something made from it may, in some cases, be much more complicated than the formula above. One example isspreading resistance profiling
Spreading resistance profiling (SRP), also known as spreading resistance analysis (SRA), is a technique used to analyze resistivity versus depth in semiconductors. Semiconductor devices depend on the distribution of carriers (electrons or electro ...
, where the material is inhomogeneous (different resistivity in different places), and the exact paths of current flow are not obvious.
In cases like this, the formulas
must be replaced with
where and are now vector fields. This equation, along with the continuity equation for and the Poisson's equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with t ...
for , form a set of partial differential equations. In special cases, an exact or approximate solution to these equations can be worked out by hand, but for very accurate answers in complex cases, computer methods like finite element analysis
The finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat ...
may be required.
Resistivity-density product
In some applications where the weight of an item is very important, the product of resistivity anddensity
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
is more important than absolute low resistivity – it is often possible to make the conductor thicker to make up for a higher resistivity; and then a low-resistivity-density-product material (or equivalently a high conductivity-to-density ratio) is desirable. For example, for long-distance overhead power line
An overhead power line is a structure used in electric power transmission and distribution to transmit electrical energy across large distances. It consists of one or more uninsulated electrical cables (commonly multiples of three for three-p ...
s, aluminium is frequently used rather than copper (Cu) because it is lighter for the same conductance.
Silver, although it is the least resistive metal known, has a high density and performs similarly to copper by this measure, but is much more expensive. Calcium and the alkali metals have the best resistivity-density products, but are rarely used for conductors due to their high reactivity with water and oxygen (and lack of physical strength). Aluminium is far more stable. Toxicity excludes the choice of beryllium. (Pure beryllium is also brittle.) Thus, aluminium is usually the metal of choice when the weight or cost of a conductor is the driving consideration.
See also
* Charge transport mechanisms *Chemiresistor
A chemiresistor is a material that changes its electrical resistance in response to changes in the nearby chemical environment. Chemiresistors are a class of chemical sensors that rely on the direct chemical interaction between the sensing material ...
* Classification of materials based on permittivity
* Conductivity near the percolation threshold
* Contact resistance
The term contact resistance refers to the contribution to the total resistance of a system which can be attributed to the contacting interfaces of electrical leads and connections as opposed to the intrinsic resistance. This effect is describe ...
* Electrical resistivities of the elements (data page)
* Electrical resistivity tomography
Electrical resistivity tomography (ERT) or electrical resistivity imaging (ERI) is a geophysical technique for imaging sub-surface structures from electrical resistivity measurements made at the surface, or by electrodes in one or more borehole ...
* Sheet resistance
Sheet resistance, is a measure of resistance of thin films that are uniform in thickness. It is commonly used to characterize materials made by semiconductor doping, metal deposition, resistive paste printing, and glass coating. Examples of thes ...
* SI electromagnetism units
* Skin effect
* Spitzer resistivity The Spitzer resistivity (or plasma resistivity) is an expression describing the electrical resistance in a plasma, which was first formulated by Lyman Spitzer in 1950. The Spitzer resistivity of a plasma decreases in proportion to the electron temp ...
* Dielectric strength
In physics, the term dielectric strength has the following meanings:
*for a pure electrically insulating material, the maximum electric field that the material can withstand under ideal conditions without undergoing electrical breakdown and beco ...
Notes
References
Further reading
*Measuring Electrical Resistivity and Conductivity
External links
*Comparison of the electrical conductivity of various elements in WolframAlpha
* {{Authority control * Physical quantities Materials science