|
Debye Temperature
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 for estimating the phonon contribution to the specific heat (Heat capacity) in a solid. It treats the vibrations of the atomic lattice (heat) as phonons in a box, in contrast to the Einstein photoelectron model, which treats the solid as many individual, non-interacting quantum harmonic oscillators. The Debye model correctly predicts the low-temperature dependence of the heat capacity of solids, which is proportional to T^3 – the Debye ''T'' 3 law. Just like the Einstein photoelectron model, it also recovers the Dulong–Petit law at high temperatures. But due to simplifying assumptions, its accuracy suffers at intermediate temperatures. Derivation The Debye model is a solid-state equivalent of Planck's law of black body photon radiation, where one treats electromagnetic photonic radiation as a photon gas. The Debye model treats atomic vibrations as phonons in a box ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Vibration
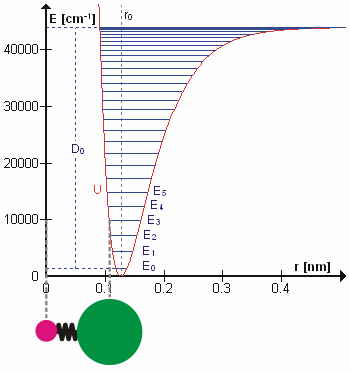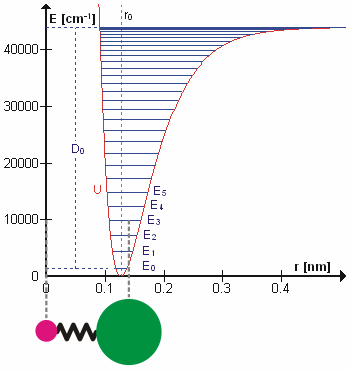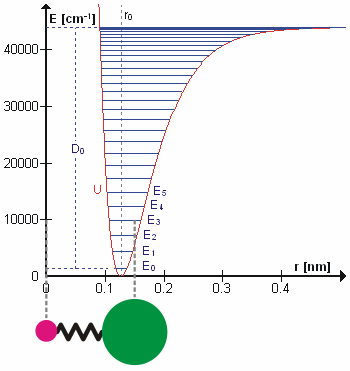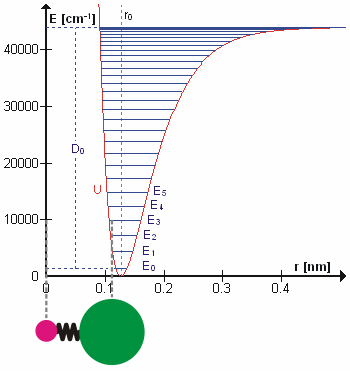
A molecular vibration is a periodic motion of the atoms of a molecule relative to each other, such that the center of mass of the molecule remains unchanged. The typical vibrational frequencies range from less than 1013 Hz to approximately 1014 Hz, corresponding to wavenumbers of approximately 300 to 3000 cm−1 and wavelengths of approximately 30 to 3 µm. For a diatomic molecule A−B, the vibrational frequency in s−1 is given by \nu = \frac \sqrt , where k is the force constant in dyne/cm or erg/cm2 and μ is the reduced mass given by \frac = \frac+\frac. The vibrational wavenumber in cm−1 is \tilde \;= \frac \sqrt, where c is the speed of light in cm/s. Vibrations of polyatomic molecules are described in terms of normal modes, which are independent of each other, but each normal mode involves simultaneous vibrations of different parts of the molecule. In general, a non-linear molecule with ''N'' atoms has 3''N'' – 6 normal modes of vibration, but a ''linear' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Phonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, specifically in solids and some liquids. A type of quasiparticle, a phonon is an excited state in the quantum mechanical quantization of the modes of vibrations for elastic structures of interacting particles. Phonons can be thought of as quantized sound waves, similar to photons as quantized light waves. The study of phonons is an important part of condensed matter physics. They play a major role in many of the physical properties of condensed matter systems, such as thermal conductivity and electrical conductivity, as well as in models of neutron scattering and related effects. The concept of phonons was introduced in 1932 by Soviet physicist Igor Tamm. The name ''phonon'' comes from the Greek word (), which translates to ''sound'' or ''voice'', because long-wavelength phonons give rise to sound. The name is analogous to the word ''photon''. Definiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sound
In physics, sound is a vibration that propagates as an acoustic wave, through a transmission medium such as a gas, liquid or solid. In human physiology and psychology, sound is the ''reception'' of such waves and their ''perception'' by the brain. Only acoustic waves that have frequencies lying between about 20 Hz and 20 kHz, the audio frequency range, elicit an auditory percept in humans. In air at atmospheric pressure, these represent sound waves with wavelengths of to . Sound waves above 20 kHz are known as ultrasound and are not audible to humans. Sound waves below 20 Hz are known as infrasound. Different animal species have varying hearing ranges. Acoustics Acoustics is the interdisciplinary science that deals with the study of mechanical waves in gasses, liquids, and solids including vibration, sound, ultrasound, and infrasound. A scientist who works in the field of acoustics is an ''acoustician'', while someone working in the field of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats. It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings, and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter '' lambda'' (λ). The term ''wavelength'' is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids. Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths. Wavelength depends on the medium (for example, vacuum, air, or water) that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inversely Proportional
In mathematics, two sequences of numbers, often experimental data, are proportional or directly proportional if their corresponding elements have a constant ratio, which is called the coefficient of proportionality or proportionality constant. Two sequences are inversely proportional if corresponding elements have a constant product, also called the coefficient of proportionality. This definition is commonly extended to related varying quantities, which are often called ''variables''. This meaning of ''variable'' is not the common meaning of the term in mathematics (see variable (mathematics)); these two different concepts share the same name for historical reasons. Two functions f(x) and g(x) are ''proportional'' if their ratio \frac is a constant function. If several pairs of variables share the same direct proportionality constant, the equation expressing the equality of these ratios is called a proportion, e.g., (for details see Ratio). Proportionality is closely ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from '' angular frequency''. Frequency is measured in hertz (Hz) which is equal to one event per second. The period is the interval of time between events, so the period is the reciprocal of the frequency. For example, if a heart beats at a frequency of 120 times a minute (2 hertz), the period, —the interval at which the beats repeat—is half a second (60 seconds divided by 120 beats). Frequency is an important parameter used in science and engineering to specify the rate of oscillatory and vibratory phenomena, such as mechanical vibrations, audio signals ( sound), radio waves, and light. Definitions and units For cyclical phenomena such as oscillations, waves, or for examples of simple harmonic motion, the term ''frequency'' is defined as the number of cycles or vibrations per unit of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Momentum
In Newtonian mechanics, momentum (more specifically linear momentum or translational momentum) is the product of the mass and velocity of an object. It is a vector quantity, possessing a magnitude and a direction. If is an object's mass and is its velocity (also a vector quantity), then the object's momentum is : \mathbf = m \mathbf. In the International System of Units (SI), the unit of measurement of momentum is the kilogram metre per second (kg⋅m/s), which is equivalent to the newton-second. Newton's second law of motion states that the rate of change of a body's momentum is equal to the net force acting on it. Momentum depends on the frame of reference, but in any inertial frame it is a ''conserved'' quantity, meaning that if a closed system is not affected by external forces, its total linear momentum does not change. Momentum is also conserved in special relativity (with a modified formula) and, in a modified form, in electrodynamics, quantum mechanics ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Three-dimensional Space
Three-dimensional space (also: 3D space, 3-space or, rarely, tri-dimensional space) is a geometric setting in which three values (called ''parameters'') are required to determine the position of an element (i.e., point). This is the informal meaning of the term dimension. In mathematics, a tuple of numbers can be understood as the Cartesian coordinates of a location in a -dimensional Euclidean space. The set of these -tuples is commonly denoted \R^n, and can be identified to the -dimensional Euclidean space. When , this space is called three-dimensional Euclidean space (or simply Euclidean space when the context is clear). It serves as a model of the physical universe (when relativity theory is not considered), in which all known matter exists. While this space remains the most compelling and useful way to model the world as it is experienced, it is only one example of a large variety of spaces in three dimensions called 3-manifolds. In this classical example, when the t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Norm (mathematics)
In mathematics, a norm is a function from a real or complex vector space to the non-negative real numbers that behaves in certain ways like the distance from the origin: it commutes with scaling, obeys a form of the triangle inequality, and is zero only at the origin. In particular, the Euclidean distance of a vector from the origin is a norm, called the Euclidean norm, or 2-norm, which may also be defined as the square root of the inner product of a vector with itself. A seminorm satisfies the first two properties of a norm, but may be zero for vectors other than the origin. A vector space with a specified norm is called a normed vector space. In a similar manner, a vector space with a seminorm is called a ''seminormed vector space''. The term pseudonorm has been used for several related meanings. It may be a synonym of "seminorm". A pseudonorm may satisfy the same axioms as a norm, with the equality replaced by an inequality "\,\leq\," in the homogeneity axiom. It ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wavelength
In physics, the wavelength is the spatial period of a periodic wave—the distance over which the wave's shape repeats. It is the distance between consecutive corresponding points of the same phase on the wave, such as two adjacent crests, troughs, or zero crossings, and is a characteristic of both traveling waves and standing waves, as well as other spatial wave patterns. The inverse of the wavelength is called the spatial frequency. Wavelength is commonly designated by the Greek letter '' lambda'' (λ). The term ''wavelength'' is also sometimes applied to modulated waves, and to the sinusoidal envelopes of modulated waves or waves formed by interference of several sinusoids. Assuming a sinusoidal wave moving at a fixed wave speed, wavelength is inversely proportional to frequency of the wave: waves with higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths. Wavelength depends on the medium (for example, vacuum, air, or water) that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |