Source Set on:
[Wikipedia]
[Google]
[Amazon]
In
 The term, "'combinatorial' appears to have been first applied to twelve-tone music by
The term, "'combinatorial' appears to have been first applied to twelve-tone music by
 A 12-tone row has hexachordal combinatoriality with another 12-tone row if their respective first (as well as second, because a 12-tone row itself forms an aggregate by definition) hexachords form an aggregate.
There are four main types of combinatoriality. A hexachord may be:
*Prime combinatorial ( transposition)
*Retrograde combinatorial ( retrograde)
*Inversional combinatorial (
A 12-tone row has hexachordal combinatoriality with another 12-tone row if their respective first (as well as second, because a 12-tone row itself forms an aggregate by definition) hexachords form an aggregate.
There are four main types of combinatoriality. A hexachord may be:
*Prime combinatorial ( transposition)
*Retrograde combinatorial ( retrograde)
*Inversional combinatorial (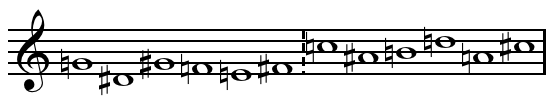 All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
Because the first three sets (''A'', ''B'', and ''C'') each satisfy all four criteria for just one transpositional value, set ''D'' satisfies them for two transpositional values, ''E'' for three values, and ''F'', for six transpositions, Babbitt designates these four groups as "first-order", "second-order", "third-order", and "sixth-order" all-combinatorial hexachords, respectively. Notice that the first set, set "A," is the first six notes of an ascending chromatic scale, and that the last set, set "F," is a whole-tone scale.
Combinatoriality may be used to create an
All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
Because the first three sets (''A'', ''B'', and ''C'') each satisfy all four criteria for just one transpositional value, set ''D'' satisfies them for two transpositional values, ''E'' for three values, and ''F'', for six transpositions, Babbitt designates these four groups as "first-order", "second-order", "third-order", and "sixth-order" all-combinatorial hexachords, respectively. Notice that the first set, set "A," is the first six notes of an ascending chromatic scale, and that the last set, set "F," is a whole-tone scale.
Combinatoriality may be used to create an
music
Music is generally defined as the art of arranging sound to create some combination of form, harmony, melody, rhythm or otherwise expressive content. Exact definitions of music vary considerably around the world, though it is an aspect ...
using the twelve tone technique
The twelve-tone technique—also known as dodecaphony, twelve-tone serialism, and (in British usage) twelve-note composition—is a method of musical composition first devised by Austrian composer Josef Matthias Hauer, who published his "law o ...
, combinatoriality is a quality shared by twelve-tone tone row
In music, a tone row or note row (german: Reihe or '), also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets ar ...
s whereby each section of a row and a proportionate number of its transformations combine to form aggregates (all twelve tones). Whittall, Arnold. 2008. ''The Cambridge Introduction to Serialism. Cambridge Introductions to Music'', p. 272. New York: Cambridge University Press. (hardback) (pbk). Much as the pitches of an aggregate created by a tone row do not need to occur simultaneously, the pitches of a combinatorially created aggregate need not occur simultaneously. Arnold Schoenberg
Arnold Schoenberg or Schönberg (, ; ; 13 September 187413 July 1951) was an Austrian-American composer, music theorist, teacher, writer, and painter. He is widely considered one of the most influential composers of the 20th century. He was as ...
, creator of the twelve-tone technique, often combined P-0/I-5 to create "two aggregates, between the first hexachord
In music, a hexachord (also hexachordon) is a six-note series, as exhibited in a scale (hexatonic or hexad) or tone row. The term was adopted in this sense during the Middle Ages and adapted in the 20th century in Milton Babbitt's serial theor ...
s of each, and the second hexachords of each, respectively."
Combinatoriality is a side effect of derived row
In music using the twelve-tone technique, derivation is the construction of a row through segments. A derived row is a tone row whose entirety of twelve tones is constructed from a segment or portion of the whole, the generator. Anton Webern often ...
s, where the initial segment or set
Set, The Set, SET or SETS may refer to:
Science, technology, and mathematics Mathematics
*Set (mathematics), a collection of elements
*Category of sets, the category whose objects and morphisms are sets and total functions, respectively
Electro ...
may be combined with its transformations (T,R,I,RI) to create an entire row. "Derivation refers to a process whereby, for instance, the initial trichord of a row can be used to arrive at a new, 'derived' row by employing the standard twelve-tone operations of transposition, inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
, retrograde, and retrograde-inversion."Christensen, Thomas (2002). ''The Cambridge History of Western Music Theory'', . Cambridge. .
Combinatorial properties are not dependent on the order of the notes within a set, but only on the content of the set, and combinatoriality may exist between three tetrachordal and between four trichord
In music theory, a trichord () is a group of three different pitch classes found within a larger group. A trichord is a contiguous three-note set from a musical scale or a twelve-tone row.
In musical set theory there are twelve trichords given ...
al sets, as well as between pairs of hexachords, and six dyads. A complement
A complement is something that completes something else.
Complement may refer specifically to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-class ...
in this context is half of a combinatorial pitch class set and most generally it is the "other half" of any pair including pitch class sets, textures, or pitch range.
Definition
Most generally complementation is the separation of pitch-class collections into two complementary sets, one containing the pitch classes not in the other. More restrictively complementation is "the process of pairing entities on either side of a center of symmetry".Kielian-Gilbert, Marianne (1982–83). "Relationships of Symmetrical Pitch-Class Sets and Stravinsky’s Metaphor of Polarity", ''Perspectives of New Music
''Perspectives of New Music'' (PNM) is a peer-reviewed academic journal specializing in music theory and analysis. It was established in 1962 by Arthur Berger and Benjamin Boretz (who were its initial editors-in-chief).
''Perspectives'' was first ...
'' 21: 210. .
 The term, "'combinatorial' appears to have been first applied to twelve-tone music by
The term, "'combinatorial' appears to have been first applied to twelve-tone music by Milton Babbitt
Milton Byron Babbitt (May 10, 1916 – January 29, 2011) was an American composer, music theorist, mathematician, and teacher. He is particularly noted for his Serialism, serial and electronic music.
Biography
Babbitt was born in Philadelphia t ...
" in 1950, when he published a review of René Leibowitz
René Leibowitz (; 17 February 1913 – 29 August 1972) was a Polish, later naturalised French, composer, conductor, music theorist and teacher. He was historically significant in promoting the music of the Second Viennese School in Paris after ...
's books ''Schoenberg et son école'' and ''Qu’est-ce que la musique de douze sons?'' Babbitt also introduced the term ''derived row''.
Hexachordal combinatoriality
 A 12-tone row has hexachordal combinatoriality with another 12-tone row if their respective first (as well as second, because a 12-tone row itself forms an aggregate by definition) hexachords form an aggregate.
There are four main types of combinatoriality. A hexachord may be:
*Prime combinatorial ( transposition)
*Retrograde combinatorial ( retrograde)
*Inversional combinatorial (
A 12-tone row has hexachordal combinatoriality with another 12-tone row if their respective first (as well as second, because a 12-tone row itself forms an aggregate by definition) hexachords form an aggregate.
There are four main types of combinatoriality. A hexachord may be:
*Prime combinatorial ( transposition)
*Retrograde combinatorial ( retrograde)
*Inversional combinatorial (inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
)
*Retrograde-inversional combinatorial ( retrograde-inversion)
and thus:
*Semi-combinatorial (by one of the above)
*All-combinatorial (by all)
Prime (transpositional) combinatoriality of a hexachord refers to the property of a hexachord whereby it forms an aggregate with one or more of its transpositions. Alternatively, transpositional combinatoriality is the lack of shared pitch classes between a hexachord and one or more of its transpositions. For example, 0 2 4 6 8 t, and its transposition up one semitone (+1): 1 3 5 7 9 e, have no notes in common.
Retrograde hexachordal combinatoriality is considered trivial, since any row has retrograde hexachordal combinatoriality with itself (''all'' tone rows have retrograde combinatoriality).
Inversional combinatoriality is a relationship between two rows, a principal row and its inversion. The principal row's first half, or six notes, are the inversion's last six notes, though not necessarily in the same order. Thus, the first half of each row is the other's complement
A complement is something that completes something else.
Complement may refer specifically to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-class ...
. The same conclusion applies to each row's second half as well. When combined, these rows still maintain a fully chromatic feeling and don't tend to reinforce certain pitches as tonal centers as might happen with freely combined rows. For example, the row from Schoenberg's ''Moses und Aron'', above contains: 0 1 4 5 6 7, this inverts to: 0 e 8 7 6 5, add three = 2 3 8 9 t e.
01 4567 : 1st hexachord P0/2nd hexachord I3
23 89te : 2nd hexachord P0/1st hexachord I3
complete chromatic scale
Retrograde-inversional combinatoriality is a lack of shared pitches between the hexachords of a row and its retrograde-inversion.
Babbitt also described the semi-combinatorial row and the all-combinatorial row, the latter being a row which is combinatorial with any of its derivations and their transpositions.
Semi-combinatorial sets are sets whose hexachords are capable of forming an aggregate with one of its basic transformations (R, I, RI) transposed. There are thirteen hexachords that are semi-combinatorial by inversion only.
(0) 0 1 2 3 4 6 // e t 9 8 7 5
(1) 0 1 2 3 5 7 // e t 9 8 6 4
(2) 0 1 2 3 6 7 // e t 9 8 5 4
(3) 0 1 2 4 5 8 // e t 9 7 6 3
(4) 0 1 2 4 6 8 // e t 9 7 5 3
(5) 0 1 2 5 7 8 // e t 9 6 4 3
(6) 0 1 3 4 6 9 // e t 8 7 5 2
(7) 0 1 3 5 7 9 // e t 8 6 4 2
(8) 0 1 3 5 8 9 // 7 6 4 2 e t
(9) 0 1 3 6 7 9 // e t 8 5 4 2
(10) 0 1 4 5 6 8 // 3 2 e t 9 7
(11) 0 2 3 4 6 8 // 1 e t 9 7 5
(12) 0 2 3 5 7 9 // 1 e t 8 6 4
Any hexachord which contains a zero in its interval vector
In musical set theory, an interval vector is an array of natural numbers which summarize the intervals present in a set of pitch classes. (That is, a set of pitches where octaves are disregarded.) Other names include: ic vector (or interva ...
possesses transpositional combinatoriality (in other words: to achieve combinatoriality a hexachord cannot be transposed by an interval equaling a note it contains). For example, there is one hexachord which is combinatorial by transposition (T6):
(0) 0 1 3 4 5 8 // 6 7 9 t e 2
Neither hexachord contains tritones.
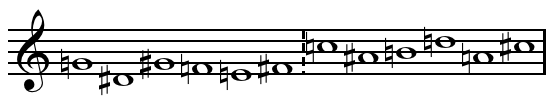 All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
Because the first three sets (''A'', ''B'', and ''C'') each satisfy all four criteria for just one transpositional value, set ''D'' satisfies them for two transpositional values, ''E'' for three values, and ''F'', for six transpositions, Babbitt designates these four groups as "first-order", "second-order", "third-order", and "sixth-order" all-combinatorial hexachords, respectively. Notice that the first set, set "A," is the first six notes of an ascending chromatic scale, and that the last set, set "F," is a whole-tone scale.
Combinatoriality may be used to create an
All-combinatorial sets are sets whose hexachords are capable of forming an aggregate with any of its basic transformations transposed.
There are six source sets, or basic hexachordally all-combinatorial sets, each hexachord of which may be reordered within itself:
(A) 0 1 2 3 4 5 // 6 7 8 9 t e
(B) 0 2 3 4 5 7 // 6 8 9 t e 1
(C) 0 2 4 5 7 9 // 6 8 t e 1 3
(D) 0 1 2 6 7 8 // 3 4 5 9 t e
(E) 0 1 4 5 8 9 // 2 3 6 7 t e
(F) 0 2 4 6 8 t // 1 3 5 7 9 e
Note: t = 10, e = 11.
Because the first three sets (''A'', ''B'', and ''C'') each satisfy all four criteria for just one transpositional value, set ''D'' satisfies them for two transpositional values, ''E'' for three values, and ''F'', for six transpositions, Babbitt designates these four groups as "first-order", "second-order", "third-order", and "sixth-order" all-combinatorial hexachords, respectively. Notice that the first set, set "A," is the first six notes of an ascending chromatic scale, and that the last set, set "F," is a whole-tone scale.
Combinatoriality may be used to create an aggregate
Aggregate or aggregates may refer to:
Computing and mathematics
* collection of objects that are bound together by a root entity, otherwise known as an aggregate root. The aggregate root guarantees the consistency of changes being made within the ...
of all twelve tones, though the term often refers simply to combinatorial rows stated together.
Hexachordal combinatoriality is a concept in post-tonal theory that describes the combination of hexachords, often used in reference to the music of the Second Viennese school
The Second Viennese School (german: Zweite Wiener Schule, Neue Wiener Schule) was the group of composers that comprised Arnold Schoenberg and his pupils, particularly Alban Berg and Anton Webern, and close associates in early 20th-century Vienna. ...
. In music that consistently utilizes all twelve chromatic tones (particularly twelve-tone and serial music
In music, serialism is a method of Musical composition, composition using series of pitches, rhythms, dynamics, timbres or other elements of music, musical elements. Serialism began primarily with Arnold Schoenberg's twelve-tone technique, thou ...
), the aggregate (collection of all 12 pitch classes) may be divided into two hexachords (collections of 6 pitches). This breaks the aggregate into two smaller pieces, thus making it easier to sequence notes, progress between rows or aggregates, and combine notes and aggregates.
Occasionally a hexachord may be combined with an inverted or transposed version of itself in a special case which will then result in the aggregate (complete set of 12 chromatic pitches).
A row (B=0: 0 6 8 5 7 e 4 3 9 t 1 2) used by Schoenberg may be divided into two hexachords:
B E F E F A // D C G G B C
When you invert the first hexachord and transpose it, the following hexachord, a reordering of the second hexachord, results:
G C B D C G = D C G G B C
Thus, when you superimpose the original hexachord 1 (P0) over the transposed inversion of hexachord 1 (I9 in this case), the entire collection of 12 pitches results. If you continued the rest of the transposed, inverted row (I9) and superimposed original hexachord 2, you would again have the full complement of 12 chromatic pitches.
Hexachordal combinatoriality is closely related to the theory of the 44 tropes created by Josef Matthias Hauer
Josef Matthias Hauer (March 19, 1883 – September 22, 1959) was an Austrian composer and music theorist. He is best known for developing, independent of and a year or two before Arnold Schoenberg, a method for composing with all 12 notes of th ...
in 1921, although it seems that Hauer had no influence on Babbitt at all. Furthermore, there is little proof suggesting that Hauer had extensive knowledge about the inversional properties of the tropes earlier than 1942 at least. The earliest records on combinatorial relations of hexachords, however, can be found amongst the theoretical writings of the Austrian composer and music theorist Othmar Steinbauer
Othmar Steinbauer (6 November 1895 – 5 September 1962) was an Austrian composer and music theorist. He progressed developments in twelve-tone composition ('). His own teachers included Joseph Marx, Anton von Webern, Arnold Schönberg and Josef ...
. He undertook elaborate studies on the trope system in the early 1930s which are documented in an unpublished typescript ''Klang- und Meloslehre'' (1932). Steinbauer's materials dated between 1932 and 1934 contain comprehensive data on combinatorial trichords, tetrachords and hexachords including semi-combinatorial and all-combinatorial sets. They may therefore be the earliest records in music history. A compilation of Steinbauer's morphological material has in parts become publicly available in 1960 with his script ''Lehrbuch der Klangreihenkomposition'' (author's edition) and was reprinted in 2001.
Trichordal combinatoriality
Trichordal combinatoriality is a row's ability to form aggregates through the combination of trichords. "Trichordal combinatoriality involves the simultaneous presentation of four rows in parcels of three pcs."Morris, Robert (1991). ''Class Notes for Atonal Music Theory'', p. 82. Frog Peak Music. . The existence of trichordal combinatoriality, or any other form, in a row does not preclude the existence of other forms of combinatoriality (at the least trivial hexachordal combinatoriality exists between every row form and its retrograde). All trichordally derived rows possess trichordal combinatoriality.Notes
Sources