Singular Boundary Method

In numerical analysis, the singular boundary method (SBM) belongs to a family of meshless boundary collocation techniques which include the method of fundamental solutions (MFS), boundary knot method (BKM), regularized meshless method (RMM), boundary particle method (BPM), modified MFS, and so on. This family of strong-form collocation methods is designed to avoid singular numerical integration and mesh generation in the traditional boundary element method (BEM) in the numerical solution of boundary value problems with boundary nodes, in which a fundamental solution of the governing equation is explicitly known.

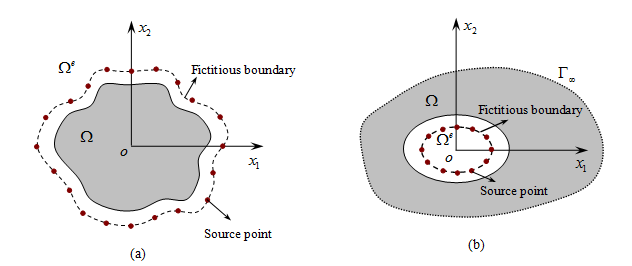
The salient feature of the SBM is to overcome the fictitious boundary in the method of fundamental solution, while keeping all merits of the latter. The method offers several advantages over the classical domain or boundary discretization methods, among which are:

* meshless. The method requires neither domain nor boundary meshing but boundary-only discretization points;
* integration-free. The numerical integration of singular or nearly singular kernels could be otherwise troublesome, expensive, and complicated, as in the case, for example, the boundary element method;
* boundary-only discretization for homogeneous problems. The SBM shares all the advantages of the BEM over domain discretization methods such as the finite element or finite difference methods;
* to overcome the perplexing fictitious boundary in the method of fundamental solutions (see Figs. 1 and 2), thanks to the introduction of the concept of the origin intensity factor, which isolates the singularity of the fundamental solutions.

The SBM provides a significant and promising alternative to popular boundary-type methods such as the BEM and MFS, in particular, for infinite domain, wave, thin-walled structures, and inverse problems.

History of the singular boundary method

The methodology of the SBM was firstly proposed by Chen and his collaborators in 2009. The basic idea is to introduce a concept of the origin intensity factor to isolate the singularity of the fundamental solutions so that the source points can be placed directly on the real boundary. In comparison, the method of fundamental solutions requires a fictitious boundary for placing the source points to avoid the singularity of fundamental solution. The SBM has since been successfully applied to a variety of physical problems, such as potential problems, infinite domain problem, Helmholtz problem, and plane elasticity problem.

There are the two techniques to evaluate the origin intensity factor. The first approach is to place a cluster of sample nodes inside the problem domain and to calculate the algebraic equations. The strategy leads to extra computational costs and makes the method is not as efficient as expected compared to the MFS. The second approach is to employ a regularization technique to cancel the singularities of the fundamental solution and its derivatives. Consequently, the origin intensity factors can be determined directly without using any sample nodes. This scheme makes the method more stable, accurate, efficient, and extends its applicability.

Recent developments

Boundary layer effect problems

Like all the other boundary-type numerical methods, also it is observed that the SBM encounters a dramatic drop of solution accuracy at the region nearby boundary. Unlike singularity at origin, the fundamental solution at near-boundary regions remains finite. However, instead of being a flat function, the interpolation function develops a sharp peak as the field point approaches the boundary. Consequently, the kernels become “nearly singular” and can not accurately be calculated. This is similar to the so-called boundary layer effect encountered in the BEM-based methods.

A nonlinear transformation, based on the sinh function, can be employed to remove or damp out the rapid variations of the nearly singular kernels.Gu Y, Chen W, Zhang J,
Investigation on near-boundary solutions by singular boundary method
, ''Eng Anal Bound Elem'' 2012;36(8): 117–82. As a result, the troublesome boundary layer effect in the SBM has been successfully remedied. The implementation of this transformation is straightforward and can easily be embedded in existing SBM programs. For the test problems studied, very promising results are obtained even when the distance between the field point and the boundary is as small as 1.

Large-scale problems

Like the MFS and BEM, the SBM will produce dense coefficient matrices, whose operation count and the memory requirements for matrix equation buildup are of the order of ''O''(''N''²) which is computationally too expensive to simulate large-scale problems.

The fast multipole method (FMM) can reduce both CPU time and memory requirement from ''O''(''N''²) to ''O''(''N'') or ''O''(''N''log''N''). With the help of FMM, the SBM can be fully capable of solving a large scale problem of several million unknowns on a desktop. This fast algorithm dramatically expands the applicable territory of the SBM to far greater problems than were previously possible.

See also

* Meshfree methods
* Radial basis function
* Trefftz method

References

External links

Kernel distance functions and radial basis functions

{{DEFAULTSORT:Singular boundary method
Numerical analysis
Numerical differential equations