Self-organizing map on:
[Wikipedia]
[Google]
[Amazon]
A self-organizing map (SOM) or self-organizing feature map (SOFM) is an unsupervised 
 This process is repeated for each input vector for a (usually large) number of cycles λ. The network winds up associating output nodes with groups or patterns in the input data set. If these patterns can be named, the names can be attached to the associated nodes in the trained net.
During mapping, there will be one single ''winning'' neuron: the neuron whose weight vector lies closest to the input vector. This can be simply determined by calculating the Euclidean distance between input vector and weight vector.
While representing input data as vectors has been emphasized in this article, any kind of object which can be represented digitally, which has an appropriate distance measure associated with it, and in which the necessary operations for training are possible can be used to construct a self-organizing map. This includes matrices, continuous functions or even other self-organizing maps.
This process is repeated for each input vector for a (usually large) number of cycles λ. The network winds up associating output nodes with groups or patterns in the input data set. If these patterns can be named, the names can be attached to the associated nodes in the trained net.
During mapping, there will be one single ''winning'' neuron: the neuron whose weight vector lies closest to the input vector. This can be simply determined by calculating the Euclidean distance between input vector and weight vector.
While representing input data as vectors has been emphasized in this article, any kind of object which can be represented digitally, which has an appropriate distance measure associated with it, and in which the necessary operations for training are possible can be used to construct a self-organizing map. This includes matrices, continuous functions or even other self-organizing maps.
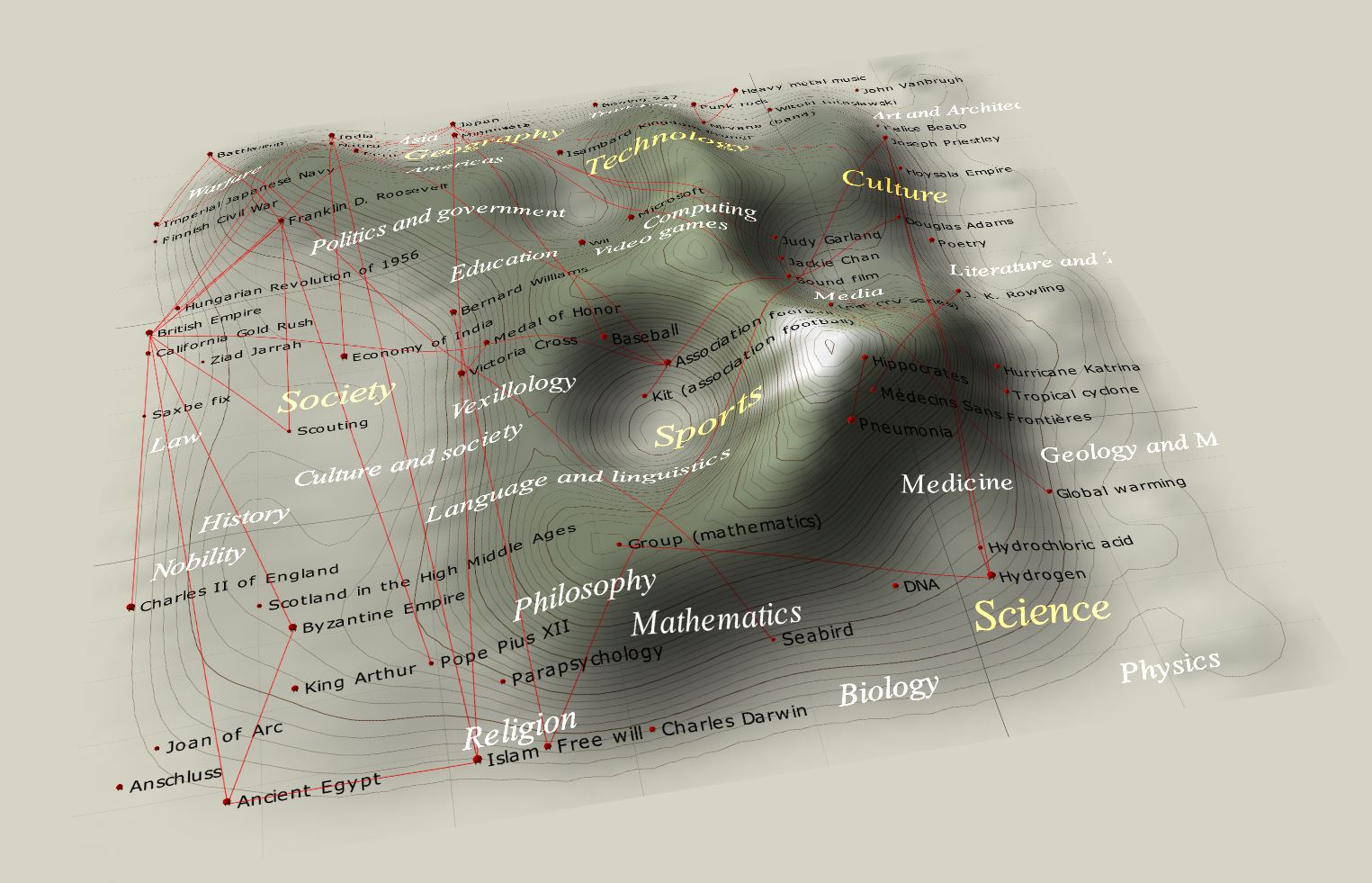 A careful comparison of random initialization to principal component initialization for a one-dimensional map, however, found that the advantages of principal component initialization are not universal. The best initialization method depends on the geometry of the specific dataset. Principal component initialization was preferable (for a one-dimensional map) when the principal curve approximating the dataset could be univalently and linearly projected on the first principal component (quasilinear sets). For nonlinear datasets, however, random initiation performed better.
A careful comparison of random initialization to principal component initialization for a one-dimensional map, however, found that the advantages of principal component initialization are not universal. The best initialization method depends on the geometry of the specific dataset. Principal component initialization was preferable (for a one-dimensional map) when the principal curve approximating the dataset could be univalently and linearly projected on the first principal component (quasilinear sets). For nonlinear datasets, however, random initiation performed better.
 There are two ways to interpret a SOM. Because in the training phase weights of the whole neighborhood are moved in the same direction, similar items tend to excite adjacent neurons. Therefore, SOM forms a semantic map where similar samples are mapped close together and dissimilar ones apart. This may be visualized by a U-Matrix (Euclidean distance between weight vectors of neighboring cells) of the SOM.
The other way is to think of neuronal weights as pointers to the input space. They form a discrete approximation of the distribution of training samples. More neurons point to regions with high training sample concentration and fewer where the samples are scarce.
SOM may be considered a nonlinear generalization of
There are two ways to interpret a SOM. Because in the training phase weights of the whole neighborhood are moved in the same direction, similar items tend to excite adjacent neurons. Therefore, SOM forms a semantic map where similar samples are mapped close together and dissimilar ones apart. This may be visualized by a U-Matrix (Euclidean distance between weight vectors of neighboring cells) of the SOM.
The other way is to think of neuronal weights as pointers to the input space. They form a discrete approximation of the distribution of training samples. More neurons point to regions with high training sample concentration and fewer where the samples are scarce.
SOM may be considered a nonlinear generalization of
Bibliography of self-organizing map (SOM) papers: 1981–1997
" ''Neural computing surveys'' 1.3&4 (1998): 1-176. * Oja, Merja, Samuel Kaski, and Teuvo Kohonen.
Bibliography of self-organizing map (SOM) papers: 1998–2001 addendum
" ''Neural computing surveys'' 3.1 (2003): 1-156.
machine learning
Machine learning (ML) is a field of study in artificial intelligence concerned with the development and study of Computational statistics, statistical algorithms that can learn from data and generalise to unseen data, and thus perform Task ( ...
technique used to produce a low-dimensional (typically two-dimensional) representation of a higher-dimensional data set while preserving the topological structure of the data. For example, a data set with variables measured in observations could be represented as clusters of observations with similar values for the variables. These clusters then could be visualized as a two-dimensional "map" such that observations in proximal clusters have more similar values than observations in distal clusters. This can make high-dimensional data easier to visualize and analyze.
An SOM is a type of artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
but is trained using competitive learning Competitive learning is a form of unsupervised learning in artificial neural networks, in which nodes compete for the right to respond to a subset of the input data. A variant of Hebbian learning, competitive learning works by increasing the special ...
rather than the error-correction learning (e.g., backpropagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates.
It is an efficient application of the chain rule to neural networks. Backpropagation computes th ...
with gradient descent
Gradient descent is a method for unconstrained mathematical optimization. It is a first-order iterative algorithm for minimizing a differentiable multivariate function.
The idea is to take repeated steps in the opposite direction of the gradi ...
) used by other artificial neural networks. The SOM was introduced by the Finnish professor Teuvo Kohonen in the 1980s and therefore is sometimes called a Kohonen map or Kohonen network. The Kohonen map or network is a computationally convenient abstraction building on biological models of neural systems from the 1970s and morphogenesis
Morphogenesis (from the Greek ''morphê'' shape and ''genesis'' creation, literally "the generation of form") is the biological process that causes a cell, tissue or organism to develop its shape. It is one of three fundamental aspects of deve ...
models dating back to Alan Turing
Alan Mathison Turing (; 23 June 1912 – 7 June 1954) was an English mathematician, computer scientist, logician, cryptanalyst, philosopher and theoretical biologist. He was highly influential in the development of theoretical computer ...
in the 1950s.
SOMs create internal representations reminiscent of the cortical homunculus, a distorted representation of the human body
The human body is the entire structure of a Human, human being. It is composed of many different types of Cell (biology), cells that together create Tissue (biology), tissues and subsequently Organ (biology), organs and then Organ system, org ...
, based on a neurological "map" of the areas and proportions of the human brain
The human brain is the central organ (anatomy), organ of the nervous system, and with the spinal cord, comprises the central nervous system. It consists of the cerebrum, the brainstem and the cerebellum. The brain controls most of the activi ...
dedicated to processing sensory functions, for different parts of the body.

Overview
Self-organizing maps, like most artificial neural networks, operate in two modes: training and mapping. First, training uses an input data set (the "input space") to generate a lower-dimensional representation of the input data (the "map space"). Second, mapping classifies additional input data using the generated map. In most cases, the goal of training is to represent an input space with ''p'' dimensions as a map space with two dimensions. Specifically, an input space with ''p'' variables is said to have ''p'' dimensions. A map space consists of components called "nodes" or "neurons", which are arranged as ahexagonal
In geometry, a hexagon (from Greek , , meaning "six", and , , meaning "corner, angle") is a six-sided polygon. The total of the internal angles of any simple (non-self-intersecting) hexagon is 720°.
Regular hexagon
A regular hexagon is d ...
or rectangular grid with two dimensions. The number of nodes and their arrangement are specified beforehand based on the larger goals of the analysis and exploration of the data.
Each node in the map space is associated with a "weight" vector, which is the position of the node in the input space. While nodes in the map space stay fixed, training consists in moving weight vectors toward the input data (reducing a distance metric such as Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
) without spoiling the topology induced from the map space. After training, the map can be used to classify additional observations for the input space by finding the node with the closest weight vector (smallest distance metric) to the input space vector.
Learning algorithm
The goal of learning in the self-organizing map is to cause different parts of the network to respond similarly to certain input patterns. This is partly motivated by how visual, auditory or other sensory information is handled in separate parts of thecerebral cortex
The cerebral cortex, also known as the cerebral mantle, is the outer layer of neural tissue of the cerebrum of the brain in humans and other mammals. It is the largest site of Neuron, neural integration in the central nervous system, and plays ...
in the human brain
The human brain is the central organ (anatomy), organ of the nervous system, and with the spinal cord, comprises the central nervous system. It consists of the cerebrum, the brainstem and the cerebellum. The brain controls most of the activi ...
.
The weights of the neurons are initialized either to small random values or sampled evenly from the subspace spanned by the two largest principal component eigenvectors
In linear algebra, an eigenvector ( ) or characteristic vector is a Vector (mathematics and physics), vector that has its direction (geometry), direction unchanged (or reversed) by a given linear map, linear transformation. More precisely, an e ...
. With the latter alternative, learning is much faster because the initial weights already give a good approximation of SOM weights.
The network must be fed a large number of example vectors that represent, as close as possible, the kinds of vectors expected during mapping. The examples are usually administered several times as iterations.
The training utilizes competitive learning Competitive learning is a form of unsupervised learning in artificial neural networks, in which nodes compete for the right to respond to a subset of the input data. A variant of Hebbian learning, competitive learning works by increasing the special ...
. When a training example is fed to the network, its Euclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
to all weight vectors is computed. The neuron whose weight vector is most similar to the input is called the best matching unit (BMU). The weights of the BMU and neurons close to it in the SOM grid are adjusted towards the input vector. The magnitude of the change decreases with time and with the grid-distance from the BMU. The update formula for a neuron v with weight vector Wv(s) is
:,
where ''s'' is the step index, ''t'' is an index into the training sample, ''u'' is the index of the BMU for the input vector D(''t''), ''α''(''s'') is a monotonically decreasing learning coefficient; ''θ''(''u'', ''v'', ''s'') is the neighborhood
A neighbourhood (Commonwealth English) or neighborhood (American English) is a geographically localized community within a larger town, city, suburb or rural area, sometimes consisting of a single street and the buildings lining it. Neigh ...
function which gives the distance between the neuron u and the neuron ''v'' in step ''s''. Depending on the implementations, t can scan the training data set systematically (''t'' is 0, 1, 2...''T''-1, then repeat, ''T'' being the training sample's size), be randomly drawn from the data set ( bootstrap sampling), or implement some other sampling method (such as jackknifing).
The neighborhood function ''θ''(''u'', ''v'', ''s'') (also called ''function of lateral interaction'') depends on the grid-distance between the BMU (neuron ''u'') and neuron ''v''. In the simplest form, it is 1 for all neurons close enough to BMU and 0 for others, but the Gaussian and Mexican-hat functions are common choices, too. Regardless of the functional form, the neighborhood function shrinks with time. At the beginning when the neighborhood is broad, the self-organizing takes place on the global scale. When the neighborhood has shrunk to just a couple of neurons, the weights are converging to local estimates. In some implementations, the learning coefficient ''α'' and the neighborhood function ''θ'' decrease steadily with increasing ''s'', in others (in particular those where ''t'' scans the training data set) they decrease in step-wise fashion, once every ''T'' steps.
 This process is repeated for each input vector for a (usually large) number of cycles λ. The network winds up associating output nodes with groups or patterns in the input data set. If these patterns can be named, the names can be attached to the associated nodes in the trained net.
During mapping, there will be one single ''winning'' neuron: the neuron whose weight vector lies closest to the input vector. This can be simply determined by calculating the Euclidean distance between input vector and weight vector.
While representing input data as vectors has been emphasized in this article, any kind of object which can be represented digitally, which has an appropriate distance measure associated with it, and in which the necessary operations for training are possible can be used to construct a self-organizing map. This includes matrices, continuous functions or even other self-organizing maps.
This process is repeated for each input vector for a (usually large) number of cycles λ. The network winds up associating output nodes with groups or patterns in the input data set. If these patterns can be named, the names can be attached to the associated nodes in the trained net.
During mapping, there will be one single ''winning'' neuron: the neuron whose weight vector lies closest to the input vector. This can be simply determined by calculating the Euclidean distance between input vector and weight vector.
While representing input data as vectors has been emphasized in this article, any kind of object which can be represented digitally, which has an appropriate distance measure associated with it, and in which the necessary operations for training are possible can be used to construct a self-organizing map. This includes matrices, continuous functions or even other self-organizing maps.
Algorithm
# Randomize the node weight vectors in a map # For ## Randomly pick an input vector ## Find the node in the map closest to the input vector. This node is the best matching unit (BMU). Denote it by ## For each node , update its vector by pulling it closer to the input vector: The variable names mean the following, with vectors in bold, * is the current iteration * is the iteration limit * is the index of the target input data vector in the input data set * is a target input data vector * is the index of the node in the map * is the current weight vector of node * is the index of the best matching unit (BMU) in the map * is the neighbourhood function, * is the learning rate schedule. The key design choices are the shape of the SOM, the neighbourhood function, and the learning rate schedule. The idea of the neighborhood function is to make it such that the BMU is updated the most, its immediate neighbors are updated a little less, and so on. The idea of the learning rate schedule is to make it so that the map updates are large at the start, and gradually stop updating. For example, if we want to learn a SOM using a square grid, we can index it using where both . The neighborhood function can make it so that the BMU updates in full, the nearest neighbors update in half, and their neighbors update in half again, etc.And we can use a simple linear learning rate schedule . Notice in particular, that the update rate does ''not'' depend on where the point is in the Euclidean space, only on where it is in the SOM itself. For example, the points are close on the SOM, so they will always update in similar ways, even when they are far apart on the Euclidean space. In contrast, even if the points end up overlapping each other (such as if the SOM looks like a folded towel), they still do not update in similar ways.Alternative algorithm
# Randomize the map's nodes' weight vectors # Traverse each input vector in the input data set ## Traverse each node in the map ### Use theEuclidean distance
In mathematics, the Euclidean distance between two points in Euclidean space is the length of the line segment between them. It can be calculated from the Cartesian coordinates of the points using the Pythagorean theorem, and therefore is o ...
formula to find the similarity between the input vector and the map's node's weight vector
### Track the node that produces the smallest distance (this node is the best matching unit, BMU)
## Update the nodes in the neighborhood of the BMU (including the BMU itself) by pulling them closer to the input vector
###
# Increase and repeat from step 2 while
Initialization options
Selection of initial weights as good approximations of the final weights is a well-known problem for all iterative methods of artificial neural networks, including self-organizing maps. Kohonen originally proposed random initiation of weights. (This approach is reflected by the algorithms described above.) More recently, principal component initialization, in which initial map weights are chosen from the space of the first principal components, has become popular due to the exact reproducibility of the results. A careful comparison of random initialization to principal component initialization for a one-dimensional map, however, found that the advantages of principal component initialization are not universal. The best initialization method depends on the geometry of the specific dataset. Principal component initialization was preferable (for a one-dimensional map) when the principal curve approximating the dataset could be univalently and linearly projected on the first principal component (quasilinear sets). For nonlinear datasets, however, random initiation performed better.
A careful comparison of random initialization to principal component initialization for a one-dimensional map, however, found that the advantages of principal component initialization are not universal. The best initialization method depends on the geometry of the specific dataset. Principal component initialization was preferable (for a one-dimensional map) when the principal curve approximating the dataset could be univalently and linearly projected on the first principal component (quasilinear sets). For nonlinear datasets, however, random initiation performed better.
Interpretation
Principal components analysis
Principal component analysis (PCA) is a Linear map, linear dimensionality reduction technique with applications in exploratory data analysis, visualization and Data Preprocessing, data preprocessing.
The data is linear map, linearly transformed ...
(PCA). It has been shown, using both artificial and real geophysical data, that SOM has many advantages over the conventional feature extraction
Feature may refer to:
Computing
* Feature recognition, could be a hole, pocket, or notch
* Feature (computer vision), could be an edge, corner or blob
* Feature (machine learning), in statistics: individual measurable properties of the phenome ...
methods such as Empirical Orthogonal Functions (EOF) or PCA. Additionally, researchers found that Clustering and PCA reflect different facets of the same local feedback circuit of human brain, with the SOM providing the shared learning rules that guide both processes. In other words, Clustering and PCA synergize via SOM.
Originally, SOM was not formulated as a solution to an optimisation problem. Nevertheless, there have been several attempts to modify the definition of SOM and to formulate an optimisation problem which gives similar results. For example, Elastic maps use the mechanical metaphor of elasticity to approximate principal manifolds: the analogy is an elastic membrane and plate.
Examples
* Banking system financial analysis * Financial investment * Project prioritization and selection * Seismic facies analysis for oil and gas exploration *Failure mode and effects analysis
Failure is the social concept of not meeting a desirable or intended Goal, objective, and is usually viewed as the opposite of success. The criteria for failure depends on context, and may be relative to a particular observer or belief system ...
*Finding representative data in large datasets
**representative species for ecological communities
**representative days for energy system models
Alternative approaches
* The generative topographic map (GTM) is a potential alternative to SOMs. In the sense that a GTM explicitly requires a smooth and continuous mapping from the input space to the map space, it is topology preserving. However, in a practical sense, this measure of topological preservation is lacking. * The growing self-organizing map (GSOM) is a growing variant of the self-organizing map. The GSOM was developed to address the issue of identifying a suitable map size in the SOM. It starts with a minimal number of nodes (usually four) and grows new nodes on the boundary based on a heuristic. By using a value called the ''spread factor'', the data analyst has the ability to control the growth of the GSOM. * The conformal map approach uses conformal mapping to interpolate each training sample between grid nodes in a continuous surface. A one-to-one smooth mapping is possible in this approach. * The time adaptive self-organizing map (TASOM) network is an extension of the basic SOM. The TASOM employs adaptive learning rates and neighborhood functions. It also includes a scaling parameter to make the network invariant to scaling, translation and rotation of the input space. The TASOM and its variants have been used in several applications including adaptive clustering, multilevel thresholding, input space approximation, and active contour modeling. Moreover, a Binary Tree TASOM or BTASOM, resembling a binary natural tree having nodes composed of TASOM networks has been proposed where the number of its levels and the number of its nodes are adaptive with its environment. * The elastic map approach borrows from thespline interpolation
In the mathematical field of numerical analysis, spline interpolation is a form of interpolation where the interpolant is a special type of piecewise polynomial called a spline. That is, instead of fitting a single, high-degree polynomial to all ...
the idea of minimization of the elastic energy
Elastic energy is the mechanical potential energy stored in the configuration of a material or physical system as it is subjected to elastic deformation by work performed upon it. Elastic energy occurs when objects are impermanently compressed ...
. In learning, it minimizes the sum of quadratic bending and stretching energy with the least squares
The method of least squares is a mathematical optimization technique that aims to determine the best fit function by minimizing the sum of the squares of the differences between the observed values and the predicted values of the model. The me ...
approximation error
The approximation error in a given data value represents the significant discrepancy that arises when an exact, true value is compared against some approximation derived for it. This inherent error in approximation can be quantified and express ...
.
* The oriented and scalable map (OS-Map) generalises the neighborhood function and the winner selection. The homogeneous Gaussian neighborhood function is replaced with the matrix exponential. Thus one can specify the orientation either in the map space or in the data space. SOM has a fixed scale (=1), so that the maps "optimally describe the domain of observation". But what about a map covering the domain twice or in n-folds? This entails the conception of scaling. The OS-Map regards the scale as a statistical description of how many best-matching nodes an input has in the map.
See also
*Deep learning
Deep learning is a subset of machine learning that focuses on utilizing multilayered neural networks to perform tasks such as classification, regression, and representation learning. The field takes inspiration from biological neuroscience a ...
* Hybrid Kohonen self-organizing map
* Learning vector quantization
* Liquid state machine
* Neocognitron
* Neural gas
* Sparse coding
* Sparse distributed memory
* Topological data analysis
Further reading
* * * * Kaski, Samuel, Jari Kangas, and Teuvo Kohonen.Bibliography of self-organizing map (SOM) papers: 1981–1997
" ''Neural computing surveys'' 1.3&4 (1998): 1-176. * Oja, Merja, Samuel Kaski, and Teuvo Kohonen.
Bibliography of self-organizing map (SOM) papers: 1998–2001 addendum
" ''Neural computing surveys'' 3.1 (2003): 1-156.
References
External links
* {{DEFAULTSORT:Self-Organizing Map Self-organization Artificial neural networks Dimension reduction Cluster analysis algorithms Finnish inventions Unsupervised learning