Quartz Crystal Microbalance on:
[Wikipedia]
[Google]
[Amazon]
A quartz crystal microbalance (QCM) (also known as ''quartz microbalance'' (QMB), sometimes also as ''quartz crystal nanobalance'' (QCN)) measures a mass variation per unit area by measuring the change in
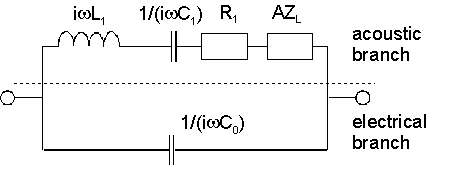 The figure on the right shows the Butterworth-van Dyke (BvD) equivalent circuit. The acoustic properties of the crystal are represented by the motional inductance, ''L''1, the motional capacitance, ''C''1, and the motional resistance ''R''1. ''Z''L is the load impedance. Note that the load, ''Z''L, cannot be determined from a single measurement. It is inferred from the comparison of the loaded and the unloaded state. Some authors use the BvD circuit without the load ''Z''L. This circuit is also called “four element network”. The values of ''L''1, ''C''1, and ''R''1 then change their value in the presence of the load (they do not if the element ''Z''L is explicitly included).
The figure on the right shows the Butterworth-van Dyke (BvD) equivalent circuit. The acoustic properties of the crystal are represented by the motional inductance, ''L''1, the motional capacitance, ''C''1, and the motional resistance ''R''1. ''Z''L is the load impedance. Note that the load, ''Z''L, cannot be determined from a single measurement. It is inferred from the comparison of the loaded and the unloaded state. Some authors use the BvD circuit without the load ''Z''L. This circuit is also called “four element network”. The values of ''L''1, ''C''1, and ''R''1 then change their value in the presence of the load (they do not if the element ''Z''L is explicitly included).
What is QCM and how does it work?
* * * {{Webarchive , url=https://archive.today/20130106005935/http://www.pc.tu-clausthal.de/en/forschung/ak-johannsmann/qcm-modellierung/ , date=January 6, 2013 , title=Tutorial on modelling the behavior of the QCM
The Principles of QCM-I with impedance analysis and dissipation monitoring (QCM-D)
QCM mini-FAQ
Weighing instruments
frequency
Frequency is the number of occurrences of a repeating event per unit of time. It is also occasionally referred to as ''temporal frequency'' for clarity, and is distinct from ''angular frequency''. Frequency is measured in hertz (Hz) which is eq ...
of a quartz crystal
Quartz is a hard, crystalline mineral composed of silica (silicon dioxide). The atoms are linked in a continuous framework of SiO4 silicon-oxygen tetrahedra, with each oxygen being shared between two tetrahedra, giving an overall chemical form ...
resonator. The resonance
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscil ...
is disturbed by the addition or removal of a small mass due to oxide growth/decay or film deposition at the surface of the acoustic resonator. The QCM can be used under vacuum, in gas phase ("gas sensor", first use described by King) and more recently in liquid environments. It is useful for monitoring the rate of deposition in thin film deposition
A thin film is a layer of material ranging from fractions of a nanometer (monolayer) to several micrometers in thickness. The controlled synthesis of materials as thin films (a process referred to as deposition) is a fundamental step in many ap ...
systems under vacuum. In liquid, it is highly effective at determining the affinity of molecules (protein
Proteins are large biomolecules and macromolecules that comprise one or more long chains of amino acid residues. Proteins perform a vast array of functions within organisms, including catalysing metabolic reactions, DNA replication, res ...
s, in particular) to surfaces functionalized with recognition sites. Larger entities such as virus
A virus is a submicroscopic infectious agent that replicates only inside the living cells of an organism. Viruses infect all life forms, from animals and plants to microorganisms, including bacteria and archaea.
Since Dmitri Ivanovsk ...
es or polymer
A polymer (; Greek '' poly-'', "many" + '' -mer'', "part")
is a substance or material consisting of very large molecules called macromolecules, composed of many repeating subunits. Due to their broad spectrum of properties, both synthetic a ...
s are investigated as well. QCM has also been used to investigate interactions between biomolecules. Frequency measurements are easily made to high precision (discussed below); hence, it is easy to measure mass densities down to a level of below 1 μg/cm2. In addition to measuring the frequency, the dissipation
In thermodynamics, dissipation is the result of an irreversible process that takes place in homogeneous thermodynamic systems. In a dissipative process, energy ( internal, bulk flow kinetic, or system potential) transforms from an initial form to ...
factor (equivalent to the resonance bandwidth) is often measured to help analysis. The dissipation factor is the inverse quality factor of the resonance, Q−1 = w/fr (see below); it quantifies the damping
Damping is an influence within or upon an oscillatory system that has the effect of reducing or preventing its oscillation. In physical systems, damping is produced by processes that dissipate the energy stored in the oscillation. Examples i ...
in the system and is related to the sample's viscoelastic
In materials science and continuum mechanics, viscoelasticity is the property of materials that exhibit both viscous and elastic characteristics when undergoing deformation. Viscous materials, like water, resist shear flow and strain linearly ...
properties.
General
Quartz
Quartz is a hard, crystalline mineral composed of silica ( silicon dioxide). The atoms are linked in a continuous framework of SiO4 silicon-oxygen tetrahedra, with each oxygen being shared between two tetrahedra, giving an overall chemical f ...
is one member of a family of crystals
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macros ...
that experience the piezoelectric effect
Piezoelectricity (, ) is the electric charge that accumulates in certain solid materials—such as crystals, certain ceramics, and biological matter such as bone, DNA, and various proteins—in response to applied mechanical stress. The word '' ...
. The piezoelectric effect has found applications in high power sources, sensors, actuators, frequency standards, motors, etc., and the relationship between applied voltage
Voltage, also known as electric pressure, electric tension, or (electric) potential difference, is the difference in electric potential between two points. In a static electric field, it corresponds to the work needed per unit of charge to ...
and mechanical deformation is well known; this allows probing an acoustic resonance by electrical means. Applying alternating current to the quartz crystal will induce oscillations. With an alternating current between the electrodes of a properly cut crystal, a standing shear wave
__NOTOC__
In seismology and other areas involving elastic waves, S waves, secondary waves, or shear waves (sometimes called elastic S waves) are a type of elastic wave and are one of the two main types of elastic body waves, so named because th ...
is generated. The Q factor
In physics and engineering, the quality factor or ''Q'' factor is a dimensionless parameter that describes how underdamped an oscillator or resonator is. It is defined as the ratio of the initial energy stored in the resonator to the energy ...
, which is the ratio of frequency and bandwidth
Bandwidth commonly refers to:
* Bandwidth (signal processing) or ''analog bandwidth'', ''frequency bandwidth'', or ''radio bandwidth'', a measure of the width of a frequency range
* Bandwidth (computing), the rate of data transfer, bit rate or thr ...
, can be as high as 106. Such a narrow resonance leads to highly stable oscillators and a high accuracy in the determination of the resonance frequency. The QCM exploits this ease and precision for sensing. Common equipment allows resolution down to 1 Hz on crystals with a fundamental resonant frequency
Resonance describes the phenomenon of increased amplitude that occurs when the frequency of an applied periodic force (or a Fourier component of it) is equal or close to a natural frequency of the system on which it acts. When an oscilla ...
in the 4 – 6 MHz range. A typical setup for the QCM contains water cooling tubes, the retaining unit, frequency sensing equipment through a microdot feed-through, an oscillation source, and a measurement and recording device.
The frequency of oscillation of the quartz crystal is partially dependent on the thickness of the crystal. During normal operation, all the other influencing variables remain constant; thus a change in thickness correlates directly to a change in frequency. As mass is deposited on the surface of the crystal, the thickness increases; consequently the frequency of oscillation decreases from the initial value. With some simplifying assumptions, this frequency change can be quantified and correlated precisely to the mass change using the Sauerbrey equation
The Sauerbrey equation was developed by the German Günter Sauerbrey in 1959, while working on his doctoral thesis at the Technical University of Berlin, Germany. It is a method for correlating changes in the oscillation frequency of a piezoelec ...
. (NB. This was partially presented at Physikertagung in Heidelberg in October 1957.) Other techniques for measuring the properties of thin films include ellipsometry
Ellipsometry is an optical technique for investigating the dielectric properties (complex refractive index or dielectric function) of thin films. Ellipsometry measures the change of polarization upon reflection or transmission and compares it t ...
, surface plasmon resonance
Surface plasmon resonance (SPR) is the resonant oscillation of conduction electrons at the interface between negative and positive permittivity material in a particle stimulated by incident light. SPR is the basis of many standard tools for measu ...
(SPR) spectroscopy
Spectroscopy is the field of study that measures and interprets the electromagnetic spectra that result from the interaction between electromagnetic radiation and matter as a function of the wavelength or frequency of the radiation. Matter ...
, Multi-Parametric Surface Plasmon Resonance and dual polarisation interferometry.
Gravimetric and non-gravimetric QCM
The classical sensing application of quartz crystal resonators is microgravimetry. Many commercial instruments, some of which are called thickness monitors, are available. These devices exploit the Sauerbrey relation. For thin films, the resonance frequency is usually inversely proportional to the total thickness of the plate. The latter increases when a film is deposited onto the crystal surface.Monolayer A monolayer is a single, closely packed layer of atoms, molecules, or cells. In some cases it is referred to as a self-assembled monolayer. Monolayers of layered crystals like graphene and molybdenum disulfide are generally called 2D materials.
C ...
sensitivity is easily reached. However, when the film thickness increases, viscoelastic effects come into play. In the late 1980s, it was recognized that the QCM can also be operated in liquids, if proper measures are taken to overcome the consequences of the large damping. Again, viscoelastic effects contribute strongly to the resonance properties.
Today, microweighing is one of several uses of the QCM.
Measurements of viscosity
The viscosity of a fluid is a measure of its resistance to deformation at a given rate. For liquids, it corresponds to the informal concept of "thickness": for example, syrup has a higher viscosity than water.
Viscosity quantifies the int ...
and more general, viscoelastic properties, are of much importance as well. The "non-gravimetric" QCM is by no means an alternative to the conventional QCM. Many researchers, who use quartz resonators for purposes other than gravimetry, have continued to call the quartz crystal resonator "QCM". Actually, the term "balance" makes sense even for non-gravimetric applications if it is understood in the sense of a force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a ...
balance. At resonance, the force exerted upon the crystal by the sample is balanced by a force originating from the shear gradient inside the crystal. This is the essence of the small-load approximation.
The QCM measures inertial mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different elementa ...
, and therefore by operating at a high resonant frequency it can be made very sensitive to small changes in that inertia as material is added to (or removed from) its surface. The sensitivity of gravitational mass measurements is, by comparison, limited by the Earth's gravitational field strength. We normally think of a balance as a way of measuring (or comparing) gravitational mass, as measured by the force that the earth exerts on the body being weighed. A few experiments have demonstrated a direct link between QCM and the SI system
The International System of Units, known by the international abbreviation SI in all languages and sometimes pleonastically as the SI system, is the modern form of the metric system and the world's most widely used system of measurement. E ...
by comparing traceable (gravitational mass) weighings with QCM measurements.
Crystalline α–quartz is by far the most important material for thickness-shear resonators. Langasite
Lanthanum gallium silicate (referred to as LGS in this article), also known as langasite, has a chemical formula of the form ''A3BC3D2O14'', where ''A'', ''B'', ''C'' and ''D'' indicate particular cation sites. ''A'' is a decahedral (Thomson cube) ...
(La3Ga5SiO14, "LGS") and
gallium-orthophosphate (GaPO4) are investigated as alternatives to quartz, mainly (but not only) for use at high temperatures. Such devices are also called "QCM", even though they are not made out of quartz (and may or may not be used for gravimetry).
Surface acoustic wave-based sensors
The QCM is a member of a wider class of sensing instruments based on acoustic waves at surfaces. Instruments sharing similar principles of operation are shear horizontalsurface acoustic wave
A surface acoustic wave (SAW) is an acoustic wave traveling along the surface of a material exhibiting elasticity, with an amplitude that typically decays exponentially with depth into the material, such that they are confined to a depth of abou ...
(SH-SAW) devices, Love-wave devices and torsional
In the field of solid mechanics, torsion is the twisting of an object due to an applied torque. Torsion is expressed in either the pascal (Pa), an SI unit for newtons per square metre, or in pounds per square inch (psi) while torque is expressed ...
resonators. Surface acoustic wave-based devices make use of the fact that the reflectivity of an acoustic wave at the crystal surface depends on the impedance (the stress-to-speed ratio) of the adjacent medium. (Some acoustic sensors for temperature or pressure make use of the fact that the speed of sound inside the crystal depends on temperature, pressure, or bending. These sensors do not exploit surface effects.) In the context of surface-acoustic wave based sensing, the QCM is also termed "bulk acoustic wave resonator (BAW-resonator)" or "thickness-shear resonator". The displacement pattern of an unloaded BAW resonator is a standing shear wave with anti-nodes at the crystal surface. This makes the analysis particularly easy and transparent.
Instrumental
Resonator crystals
When the QCM was first developed, natural quartz was harvested, selected for its quality and then cut in the lab. However, most of today's crystals are grown using seed crystals. A seed crystal serves as an anchoring point and template for crystal growth. Grown crystals are subsequently cut and polished into hair-thin discs which support thickness shear resonance in the 1-30 MHz range. The "AT" or "SC" oriented cuts (discussed below) are widely used in applications.Electromechanical coupling
The QCM consists of a thin piezoelectric plate with electrodes evaporated onto both sides. Due to the piezo-effect, an AC voltage across the electrodes induces a shear deformation and vice versa. The electromechanical coupling provides a simple way to detect an acoustic resonance by electrical means. Otherwise, it is of minor importance. However, electromechanical coupling can have a slight influence on the resonance frequency via piezoelectric stiffening. This effect can be used for sensing, but is usually avoided. It is essential to have the electric anddielectric
In electromagnetism, a dielectric (or dielectric medium) is an electrical insulator that can be polarised by an applied electric field. When a dielectric material is placed in an electric field, electric charges do not flow through the mate ...
boundary conditions well under control. Grounding the front electrode (the electrode in contact with the sample) is one option. A π-network sometimes is employed for the same reason.IEC standard 60444-1 A π-network is an arrangement of resistor
A resistor is a passive two-terminal electrical component that implements electrical resistance as a circuit element. In electronic circuits, resistors are used to reduce current flow, adjust signal levels, to divide voltages, bias active el ...
s, which almost short-circuit
A short circuit (sometimes abbreviated to short or s/c) is an electrical circuit that allows a current to travel along an unintended path with no or very low electrical impedance. This results in an excessive current flowing through the circuit. ...
the two electrodes. This makes the device less susceptible to electrical perturbations.
Shear waves decay in liquids and gases
Most acoustic-wave-based sensors employ shear (transverse) waves. Shear waves decay rapidly in liquid and gaseous environments. Compressional (longitudinal) waves would be radiated into the bulk and potentially be reflected back to the crystal from the opposing cell wall. Such reflections are avoided with transverse waves. The range of penetration of a 5 MHz-shear wave in water is 250 nm. This finite penetration depth renders the QCM surface-specific. Also, liquids and gases have a rather small shear-acoustic impedance and therefore only weakly damp the oscillation. The exceptionally high Q-factors of acoustic resonators are linked to their weak coupling to the environment.Modes of operation
Economic ways of driving a QCM make use of oscillator circuits. Oscillator circuits are also widely employed in time and frequency control applications, where the oscillator serves as a clock. Other modes of operation are impedance analysis, QCM-I, and ring-down, QCM-D. In impedance analysis, theelectric conductance
The electrical resistance of an object is a measure of its opposition to the flow of electric current. Its reciprocal quantity is , measuring the ease with which an electric current passes. Electrical resistance shares some conceptual parallel ...
as a function of driving frequency is determined by means of a network analyzer. By fitting a resonance curve to the conductance curve, one obtains the frequency and bandwidth of the resonance as fit parameters. In ring-down, one measures the voltage between the electrodes after the exciting voltage has suddenly been turned off. The resonator emits a decaying sine wave
A sine wave, sinusoidal wave, or just sinusoid is a curve, mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph of a function, graph. It is a type of continuous wave and also a Smoothness, smooth p ...
, where the resonance parameters are extracted from the period of oscillation and the decay rate.
Energy trapping
The electrodes at the front and the back of the crystal usually are key-hole shaped, thereby making the resonator thicker in the center than at the rim. The mass of the electrodes confines the displacement field to the center of the crystal disk by a mechanism called energy trapping. The thickness-shear vibration amplitude is greatest at the center of the disk. This means that the mass-sensitivity is peaked at the center also, with this sensitivity declining smoothly to zero just outside the perimeter of the smallest electrode. The mass-sensitivity is therefore very non-uniform across the crystal surface, and this non-uniformity is a function of the mass-distribution of the metal electrodes (or in the case of non-planar resonators, the quartz crystal thickness itself). Energy trapping turns the crystal turns into an acoustic lens and the wave is focused to the center of the crystal. Energy trapping is necessary in order to be able to mount the crystal at the edge without excessive damping. Energy trapping slightly distorts the otherwise planar wave fronts. The deviation from the plane thickness-shear mode entails flexural contribution to the displacement pattern. Flexural waves emit compressional waves into the adjacent medium, which is a problem when operating the crystal in a liquid environment.Overtones
Planar resonators can be operated at a number ofovertone
An overtone is any resonant frequency above the fundamental frequency of a sound. (An overtone may or may not be a harmonic) In other words, overtones are all pitches higher than the lowest pitch within an individual sound; the fundamental i ...
s, typically indexed by the number of nodal planes parallel to the crystal surfaces. Only odd harmonic
A harmonic is a wave with a frequency that is a positive integer multiple of the ''fundamental frequency'', the frequency of the original periodic signal, such as a sinusoidal wave. The original signal is also called the ''1st harmonic'', the ...
s can be excited electrically because only these induce charges of opposite sign at the two crystal surfaces. Overtones are to be distinguished from anharmonic side bands (spurious modes), which have nodal planes perpendicular to the plane of the resonator. The best agreement between theory and experiment is reached with planar, optically polished crystals for overtone orders between ''n'' = 5 and ''n'' = 13. On low harmonics, energy trapping is insufficient, while on high harmonics, anharmonic side bands interfere with the main resonance.
Amplitude of motion
Theamplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
of lateral displacement rarely exceeds a nanometer. More specifically one has
with ''u''0 the amplitude of lateral displacement, ''n'' the overtone order, ''d'' the piezoelectric strain coefficient, ''Q'' the quality factor, and ''U''el the amplitude of electrical driving. The piezoelectric strain coefficient is given as ''d'' = 3.1·10‑12 m/V for AT-cut quartz crystals. Due to the small amplitude, stress
Stress may refer to:
Science and medicine
* Stress (biology), an organism's response to a stressor such as an environmental condition
* Stress (linguistics), relative emphasis or prominence given to a syllable in a word, or to a word in a phrase ...
and strain
Strain may refer to:
Science and technology
* Strain (biology), variants of plants, viruses or bacteria; or an inbred animal used for experimental purposes
* Strain (chemistry), a chemical stress of a molecule
* Strain (injury), an injury to a mu ...
usually are proportional to each other. The QCM operates in the range of linear acoustics.
Effects of temperature and stress
The resonance frequency of acoustic resonators depends on temperature, pressure, and bending stress. Temperature-frequency coupling is minimized by employing special crystal cuts. A widely used temperature-compensated cut of quartz is the AT-cut. Careful control of temperature and stress is essential in the operation of the QCM. AT-cut crystals are singularly rotated Y-axis cuts in which the top and bottom half of the crystal move in opposite directions (thickness shear vibration) during oscillation. The AT-cut crystal is easily manufactured. However, it has limitations at high and low temperature, as it is easily disrupted by internal stresses caused by temperature gradients in these temperature extremes (relative to room temperature, ~25 °C). These internal stress points produce undesirable frequency shifts in the crystal, decreasing its accuracy. The relationship between temperature and frequency is cubic. The cubic relationship has aninflection point
In differential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (British English: inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of ...
near room temperature. As a consequence the AT-cut quartz crystal is most effective when operating at or near room temperature. For applications which are above room temperature, water cooling is often helpful.
Stress-compensated (SC) crystals are available with a doubly rotated cut that minimizes the frequency changes due to temperature gradients when the system is operating at high temperatures, and reduces the reliance on water cooling. (NB. Possible mixup of sources? While all three authors and the journal exist (and they published elsewhere in this journal), the existence of this particular article needs to be verified as it could not be found in online repositories so far.) SC-cut crystals have an inflection point of ~92 °C. In addition to their high temperature inflection point, they also have a smoother cubic relationship and are less affected by temperature deviations from the inflection point. However, due to the more difficult manufacturing process, they are more expensive and are not widely commercially available.
Electrochemical QCM
The QCM can be combined with other surface-analytical instruments. Theelectrochemical
Electrochemistry is the branch of physical chemistry concerned with the relationship between electrical potential difference, as a measurable and quantitative phenomenon, and identifiable chemical change, with the potential difference as an outc ...
QCM (EQCM) is particularly advanced. Using the EQCM, one determines the ratio of mass deposited at the electrode surface during an electrochemical reaction to the total charge passed through the electrode. This ratio is called the current efficiency.
Quantification of dissipative processes
For advanced QCMs, such as QCM-I and QCM-D, both the resonance frequency, ''f''r, and the bandwidth, ''w'', are available for analysis. The latter quantifies processes which withdraw energy from the oscillation. These may include damping by the holder and ohmic losses inside the electrode or the crystal. In the literature some parameters other than ''w'' itself are used to quantify bandwidth. The Q-factor (quality factor) is given by ''Q'' = ''f''r/''w''. The “dissipation factor”, ''D'', is the inverse of the Q-factor: ''D'' = ''Q''−1 = ''w''/''f''r. The half-band-half-width, Γ, is Γ = ''w''/2. The use of Γ is motivated by a complex formulation of the equations governing the motion of the crystal. Acomplex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
resonance frequency is defined as ''f''r* = ''f''r + iΓ, where the imaginary part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
, Γ, is half the bandwidth at half maximum. Using a complex notation, one can treat shifts of frequency, Δ''f'', and bandwidth, ΔΓ, within the same set of (complex) equations.
The motional resistance of the resonator, ''R''1, is also used as a measure of dissipation. ''R''1 is an output parameter of some instruments based on advanced oscillator circuits. ''R''1 usually is not strictly proportional to the bandwidth (although it should be according to the BvD circuit; see below). Also, in absolute terms, ''R''1 – being an electrical quantity and not a frequency – is more severely affected by calibration
In measurement technology and metrology, calibration is the comparison of measurement values delivered by a device under test with those of a calibration standard of known accuracy. Such a standard could be another measurement device of know ...
problems than the bandwidth.
Equivalent circuits
Modeling of acoustic resonators often occurs with equivalentelectrical circuits
An electrical network is an interconnection of electrical components (e.g., batteries, resistors, inductors, capacitors, switches, transistors) or a model of such an interconnection, consisting of electrical elements (e.g., voltage sources, c ...
. (NB. Originally published as volume VIa/4 of .) Equivalent circuits are algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
ically equivalent to the continuum mechanics
Continuum mechanics is a branch of mechanics that deals with the mechanical behavior of materials modeled as a continuous mass rather than as discrete particles. The French mathematician Augustin-Louis Cauchy was the first to formulate such m ...
description and to a description in terms of acoustic reflectivities. They provide for a graphical representation of the resonator's properties and their shifts upon loading. These representations are not just cartoons. They are tools to predict the shift of the resonance parameters in response to the addition of the load.
Equivalent circuits build on the electromechanical analogy
Analogy (from Greek ''analogia'', "proportion", from ''ana-'' "upon, according to" lso "against", "anew"+ ''logos'' "ratio" lso "word, speech, reckoning" is a cognitive process of transferring information or meaning from a particular subject ( ...
. In the same way as the current through a network of resistors can be predicted from their arrangement and the applied voltage, the displacement of a network of mechanical elements can be predicted from the topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such ...
of the network and the applied force. The electro-mechanical analogy maps forces onto voltages and speeds onto currents. The ratio of force and speed is termed "mechanical impedance
Mechanical impedance is a measure of how much a structure resists motion when subjected to a harmonic force. It relates forces with velocities acting on a mechanical system. The mechanical impedance of a point on a structure is the ratio of the for ...
". Note: Here, speed means the time derivative of a displacement, not the speed of sound. There also is an electro-acoustic analogy, within which stresses (rather than forces) are mapped onto voltages. In acoustics, forces are normalized to area. The ratio of stress and speed should not be called "acoustic impedance
Acoustic impedance and specific acoustic impedance are measures of the opposition that a system presents to the acoustic flow resulting from an acoustic pressure applied to the system. The SI unit of acoustic impedance is the pascal-second per cub ...
" (in analogy to the mechanical impedance) because this term is already in use for the material property ''Z''ac = ρ''c'' with ρ the density
Density (volumetric mass density or specific mass) is the substance's mass per unit of volume. The symbol most often used for density is ''ρ'' (the lower case Greek letter rho), although the Latin letter ''D'' can also be used. Mathematical ...
and ''c'' the speed of sound). The ratio of stress and speed at the crystal surface is called load impedance, ''Z''L. Synonymous terms are "surface impedance" and "acoustic load." The load impedance is in general not equal to the material constant ''Z''ac = ρ''c'' = (''G''ρ)1/2. Only for propagating plane waves are the values of ''Z''L and ''Z''ac the same.
The electro-mechanical analogy provides for mechanical equivalents of a resistor, an inductance
Inductance is the tendency of an electrical conductor to oppose a change in the electric current flowing through it. The flow of electric current creates a magnetic field around the conductor. The field strength depends on the magnitude of the ...
, and a capacitance
Capacitance is the capability of a material object or device to store electric charge. It is measured by the change in charge in response to a difference in electric potential, expressed as the ratio of those quantities. Commonly recognized are ...
, which are the dashpot
A dashpot, also known as a damper, is a mechanical device that resists motion via viscous friction. The resulting force is proportional to the velocity, but acts in the opposite direction, slowing the motion and absorbing energy. It is commonly us ...
(quantified by the drag coefficient
In fluid dynamics, the drag coefficient (commonly denoted as: c_\mathrm, c_x or c_) is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment, such as air or water. It is used in the drag equ ...
, ξp), the point mass (quantified by the mass, ''m''p), and the spring
Spring(s) may refer to:
Common uses
* Spring (season)
Spring, also known as springtime, is one of the four temperate seasons, succeeding winter and preceding summer. There are various technical definitions of spring, but local usage of ...
(quantified by the spring constant
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring (device), spring by some distance () Proportionality (mathematics)#Direct_proportionality, scales linearly with respect to that ...
, κp). For a dashpot, the impedance by definition is ''Z''m=''F'' / (d''u''/d''t'')=ξm with ''F'' the force and (d''u''/d''t'') the speed). For a point mass undergoing oscillatory motion ''u''(''t'') = ''u''0 exp(iω''t'') we have ''Z''m = iω''m''p. The spring obeys ''Z''m =κp/(iω). Piezoelectric coupling is depicted as a transformer
A transformer is a passive component that transfers electrical energy from one electrical circuit to another circuit, or multiple circuits. A varying current in any coil of the transformer produces a varying magnetic flux in the transformer' ...
. It is characterized by a parameter φ. While φ is dimensionless for usual transformers (the turns ratio), it has the dimension charge/length in the case of electromechanical coupling. The transformer acts as an impedance converter in the sense that a mechanical impedance, ''Z''m, appears as an electrical impedance, ''Z''el, across the electrical ports. '' Z''el is given by ''Z''el = φ2 ''Z''m. For planar piezoelectric crystals, φ takes the value φ = ''Ae''/''d''q, where ''A'' is the effective area, ''e'' is the piezoelectric stress coefficient (''e'' = 9.65·10−2 C/m2 for AT-cut quartz) and ''d''q is the thickness of the plate. The transformer often is not explicitly depicted. Rather, the mechanical elements are directly depicted as electrical elements (capacitor replaces a spring, etc.).
There is a pitfall with the application of the electro-mechanical analogy, which has to do with how networks are drawn. When a spring pulls onto a dashpot, one would usually draw the two elements in series. However, when applying the electro-mechanical analogy, the two elements have to be placed in parallel. For two parallel electrical elements the currents are additive. Since the speeds (= currents) add when placing a spring behind a dashpot, this assembly has to be represented by a parallel network.
 The figure on the right shows the Butterworth-van Dyke (BvD) equivalent circuit. The acoustic properties of the crystal are represented by the motional inductance, ''L''1, the motional capacitance, ''C''1, and the motional resistance ''R''1. ''Z''L is the load impedance. Note that the load, ''Z''L, cannot be determined from a single measurement. It is inferred from the comparison of the loaded and the unloaded state. Some authors use the BvD circuit without the load ''Z''L. This circuit is also called “four element network”. The values of ''L''1, ''C''1, and ''R''1 then change their value in the presence of the load (they do not if the element ''Z''L is explicitly included).
The figure on the right shows the Butterworth-van Dyke (BvD) equivalent circuit. The acoustic properties of the crystal are represented by the motional inductance, ''L''1, the motional capacitance, ''C''1, and the motional resistance ''R''1. ''Z''L is the load impedance. Note that the load, ''Z''L, cannot be determined from a single measurement. It is inferred from the comparison of the loaded and the unloaded state. Some authors use the BvD circuit without the load ''Z''L. This circuit is also called “four element network”. The values of ''L''1, ''C''1, and ''R''1 then change their value in the presence of the load (they do not if the element ''Z''L is explicitly included).
Small-load approximation
The BvD circuit predicts the resonance parameters. One can show that the following simple relation holds as long as the frequency shift is much smaller than the frequency itself: ''f''f is the frequency of thefundamental
Fundamental may refer to:
* Foundation of reality
* Fundamental frequency, as in music or phonetics, often referred to as simply a "fundamental"
* Fundamentalism, the belief in, and usually the strict adherence to, the simple or "fundamental" idea ...
. ''Z''q is the acoustic impedance of material. For AT-cut quartz, its value is ''Z''q = 8.8·106 kg m−2 s−1.
The small-load approximation is central to the interpretation of QCM-data. It holds for arbitrary samples and can be applied in an average sense.Heterogeneous samples will, in general, lead to scattering of acoustic waves, which is not captured by just calculating the average stress. Assume that the sample is a complex material, such as a cell culture
Cell culture or tissue culture is the process by which cells are grown under controlled conditions, generally outside of their natural environment. The term "tissue culture" was coined by American pathologist Montrose Thomas Burrows. This te ...
, a sand pile, a froth, an assembly of spheres or vesicles
Vesicle may refer to:
; In cellular biology or chemistry
* Vesicle (biology and chemistry), a supramolecular assembly of lipid molecules, like a cell membrane
* Synaptic vesicle
; In human embryology
* Vesicle (embryology), bulge-like features o ...
, or a droplet. If the average stress-to-speed ratio of the sample at the crystal surface (the load impedance, ''Z''L) can be calculated in one way or another, a quantitative analysis of the QCM experiment is in reach. Otherwise, the interpretation will have to remain qualitative.
The limits of the small-load approximation are noticed either when the frequency shift is large or when the overtone-dependence of Δ''f'' and Δ(''w''/2) is analyzed in detail in order to derive the viscoelastic properties of the sample. A more general relation is
This equation is implicit
Implicit may refer to:
Mathematics
* Implicit function
* Implicit function theorem
* Implicit curve
* Implicit surface
* Implicit differential equation
Other uses
* Implicit assumption, in logic
* Implicit-association test, in social psychology
...
in Δ''f''*, and must be solved numerically. Approximate solutions also exist, which go beyond the small-load approximation. The small-load approximation is the first order solution of a perturbation analysis
In mathematics and applied mathematics, perturbation theory comprises methods for finding an approximate solution to a problem, by starting from the exact solution of a related, simpler problem. A critical feature of the technique is a middle ...
.
The definition of the load impedance implicitly assumes that stress and speed are proportional and that the ratio therefore is independent of speed. This assumption is justified when the crystal is operated in liquids and in air. The laws of linear acoustics then hold. However, when the crystal is in contact with a rough surface, stress can easily become a nonlinear function
In mathematics and science, a nonlinear system is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other ...
of strain (and speed) because the stress is transmitted across a finite number of rather small load-bearing asperities. The stress at the points of contact is high, and phenomena like slip, partial slip, yield, etc. set in. These are part of non-linear acoustics. There is a generalization of the small-load equation dealing with this problem. If the stress, σ(''t''), is periodic in time and synchronous with the crystal oscillation one has
Angular brackets denote a time average and σ(''t'') is the (small) stress exerted by the external surface. The function σ(t) may or may not be harmonic. One can always test for nonlinear behavior by checking for a dependence of the resonance parameters on the driving voltage. If linear acoustics hold, there is no drive level-dependence. Note, however, that quartz crystals have an intrinsic drive level-dependence, which must not be confused with nonlinear interactions between the crystal and the sample.
Viscoelastic modeling
Assumptions
For a number of experimental configurations, there are explicit expressions relating the shifts of frequency and bandwidth to the sample properties. The assumptions underlying the equations are the following: * The resonator and all cover layers are laterally homogeneous and infinite. * The distortion of the crystal is given by a transverse plane wave with thewave-vector
In physics, a wave vector (or wavevector) is a vector used in describing a wave, with a typical unit being cycle per metre. It has a magnitude and direction. Its magnitude is the wavenumber of the wave (inversely proportional to the wavelength), ...
perpendicular to the surface normal (thickness-shear mode). There are neither compressional waves nor flexural contributions to the displacement pattern. There are no nodal lines in the plane of the resonator.
* All stresses are proportional to strain. Linear viscoelasticity holds. (NB. V. V. Borovikov translates to in Cyrillic.)
* Piezoelectric stiffening may be ignored.
Semi-infinite viscoelastic medium
For a semi-infinite medium, one has η’ and η’’ are thereal
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010) ...
and the imaginary part
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
of the viscosity, respectively. ''Z''ac = ρ''c'' =(''G'' ρ)1/2 is the acoustic impedance of the medium. ρ is the density, ''c'', the speed of sound, and ''G'' = i ωη is the shear modulus
In materials science, shear modulus or modulus of rigidity, denoted by ''G'', or sometimes ''S'' or ''μ'', is a measure of the elastic shear stiffness of a material and is defined as the ratio of shear stress to the shear strain:
:G \ \stackrel ...
.
For Newtonian liquids (η’ = const, η’’ = 0), Δ''f'' and Δ(''w''/2) are equal and opposite. They scale as the square root of the overtone order, ''n''1/2. For viscoelastic liquids (η’ = η(ω), η’’≠ 0), the complex viscosity can be obtained as
Importantly, the QCM only probes the region close to the crystal surface. The shear wave evanescently decays into the liquid. In water the penetration depth is about 250 nm at 5 MHz. Surface roughness, nano-bubbles at the surface, slip, and compressional waves can interfere with the measurement of viscosity. Also, the viscosity determined at MHz frequencies sometimes differs from the low-frequency viscosity. In this respect, torsional resonators (with a frequency around 100 kHz) are closer to application than thickness-shear resonators.
Inertial loading (Sauerbrey equation)
The frequency shift induced by a thin sample which is rigidly coupled to the crystal (such as a thin film), is described by theSauerbrey equation
The Sauerbrey equation was developed by the German Günter Sauerbrey in 1959, while working on his doctoral thesis at the Technical University of Berlin, Germany. It is a method for correlating changes in the oscillation frequency of a piezoelec ...
. The stress is governed by inertia
Inertia is the idea that an object will continue its current motion until some force causes its speed or direction to change. The term is properly understood as shorthand for "the principle of inertia" as described by Newton in his first law ...
, which implies σ = -ω2''u''0''m''F, where ''u''0 is the amplitude of oscillation and ''m''F is the (average) mass per unit area. Inserting this result into the small-load-approximation one finds
If the density of the film is known, one can convert from mass per unit area, ''m''F, to thickness, ''d''F. The thickness thus derived is also called the Sauerbrey thickness A quartz crystal microbalance (QCM) (also known as ''quartz microbalance'' (QMB), sometimes also as ''quartz crystal nanobalance'' (QCN)) measures a mass variation per unit area by measuring the change in frequency of a quartz crystal resonator. The ...
to show that it was derived by applying the Sauerbrey equation to the frequency shift.
The shift in bandwidth is zero if the Sauerbrey equation holds. Checking for the bandwidth therefore amounts to checking the applicability of the Sauerbrey equation.
The Sauerbrey equation was first derived by Günter Sauerbrey in 1959 and correlates changes in the oscillation frequency of a piezoelectric crystal with mass deposited on it. He simultaneously developed a method for measuring the resonance frequency and its changes by using the crystal as the frequency-determining component of an oscillator circuit. His method continues to be used as the primary tool in quartz crystal microbalance experiments for conversion of frequency to mass.
Because the film is treated as an extension of thickness, Sauerbrey’s equation only applies to systems in which (a) the deposited mass has the same acoustic properties as the crystal and (b) the frequency change is small (Δ''f'' / ''f'' < 0.05).
If the change in frequency is greater than 5%, that is, Δ''f'' / ''f'' > 0.05, the Z-match method must be used to determine the change in mass. The formula for the Z-match method is:
''k''F is the wave vector inside the film and ''d''F its thickness. Inserting ''k''F = 2·π·''f'' /cF = 2·π·''f''·ρF / ''Z''F as well as ''d''F = ''m''F / ρF yields
Viscoelastic film
For a viscoelastic film, the frequency shift is Here ''Z''F is the acoustic impedance of the film (''Z''F = ρF''c''F = (ρF''G''f)1/2)= (ρF/''J''f)1/2), ''k''F is the wave vector and ''d''F is the film thickness. ''J''f is the film's viscoelastic compliance, ρF is the density. The poles of thetangent
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
(''k''F ''d''F = π/2) define the film resonances. At the film resonance, one has ''d''F = λ/4. The agreement between experiment and theory is often poor close to the film resonance. Typically, the QCM only works well for film thicknesses much less than a quarter of the wavelength of sound (corresponding to a few micrometres, depending on the softness of the film and the overtone order).
Note that the properties of a film as determined with the QCM are fully specified by two parameters, which are its acoustic impedance, ''Z''F = ρF''c''F and its mass per unit area, ''m''F = ''d''F/ρF. The wave number ''k''F = ω/''c''F is not algebraically independent from ''Z''F and ''m''F. Unless the density of the film is known independently, the QCM can only measure mass per unit area, never the geometric thickness itself.
Viscoelastic film in liquid
For a film immersed in a liquid environment, the frequency shift is The indices ''F'' and ''Liq'' denote the film and the liquid. Here, the reference state is the crystal immersed in liquid (but not covered with a film). For thin films, one can Taylor-expand the above equation to first order in ''d''F, yielding Apart from the term in brackets, this equation is equivalent to the Sauerbrey equation. The term in brackets is a viscoelastic correction, dealing with the fact that in liquids, soft layers lead to a smaller Sauerbrey thickness than rigid layers.Derivation of viscoelastic constants
The frequency shift depends on the acoustic impedance of the material; the latter in turn depends on the viscoelastic properties of the material. Therefore, in principle, one can derive the complex shear modulus (or equivalently, the complex viscosity). However, there are certain caveats to be kept in mind: * The viscoelastic parameters themselves usually depend on frequency (and therefore on the overtone order). * It is often difficult to disentangle effects of inertia and viscoelasticity. Unless the film thickness is known independently, it is difficult to obtain unique fitting results. * Electrode effects can be of importance. * For films in air, the small-load approximation must be replaced by the corresponding results from perturbation theory unless the films are very soft. For thin films in liquids, there is an approximate analytical result, relating the elastic compliance of the film, ''J''F’ to the ratio of Δ(w/2); and Δ''f''. The shear compliance is the inverse of the shear modulus, ''G''. In the thin-film limit, the ratio of Δ(w/2) and –Δ''f'' is independent of film thickness. It is an intrinsic property of the film. One has For thin films in air an analogous analytical result is Here ''J''’’ is the viscous shear compliance.Interpretation of the Sauerbrey thickness
The correct interpretation of the frequency shift from QCM experiments in liquids is a challenge. Practitioners often just apply the Sauerbrey equation to their data and term the resulting areal mass (mass per unit area) the " Sauerbrey mass" and the corresponding thickness "Sauerbrey thickness". Even though the Sauerbrey thickness can certainly serve to compare different experiments, it must not be naively identified with the geometric thickness. Worthwhile considerations are the following: a) The QCM always measures an areal mass density, never a geometric thickness. The conversion from areal mass density to thickness usually requires the physical density as an independent input. b) It is difficult to infer the viscoelastic correction factor from QCM data. However, if the correction factor differs significantly from unity, it may be expected that it affects the bandwidth Δ(w/2) and also that it depends on overtone order. If, conversely, such effects are absent (Δ(''w''/2) « Δ''f'', Sauerbrey thickness same on all overtone orders) one may assume that (1-''Z''Liq2/''Z''F2)≈1. c) Complex samples are often laterally heterogeneous. d) Complex samples often have fuzzy interfaces. A "fluffy" interface will often lead to a viscoelastic correction and, as a consequence, to a non-zero Δ(''w''/2) as well as an overtone-dependent Sauerbrey mass. In the absence of such effects, one may conclude that the outer interface of film is sharp. e) When the viscoelastic correction, as discussed in (b), is insignificant, this does by no means imply that the film is not swollen by thesolvent
A solvent (s) (from the Latin '' solvō'', "loosen, untie, solve") is a substance that dissolves a solute, resulting in a solution. A solvent is usually a liquid but can also be a solid, a gas, or a supercritical fluid. Water is a solvent for ...
. It only means that the (swollen) film is much more rigid than the ambient liquid. QCM data taken on the wet sample alone do not allow inference of the degree of swelling. The amount of swelling can be inferred from the comparison of the wet and the dry thickness. The degree of swelling is also accessible by comparing the acoustic thickness (in the Sauerbrey sense) to the optical thickness as determined by, for example, surface plasmon resonance (SPR) spectroscopy or ellipsometry. Solvent contained in the film usually does contribute to the acoustic thickness (because it takes part in the movement), whereas it does not contribute to the optic thickness (because the electronic polarizability
Polarizability usually refers to the tendency of matter, when subjected to an electric field, to acquire an electric dipole moment in proportion to that applied field. It is a property of all matter, considering that matter is made up of elementar ...
of a solvent molecule does not change when it is located inside a film). The difference in dry and wet mass is shown with QCM-D and MP-SPR for instance in protein adsorption on nanocellulose and in other soft materials.
Point contacts
The equations concerning viscoelastic properties assume planar layer systems. A frequency shift is also induced when the crystal makes contact with discrete objects across small, load-bearing asperities. Such contacts are often encountered with rough surfaces. It is assumed that the stress–speed ratio may be replaced by an average stress–speed ratio, where the average stress just is the lateral force divided by the active area of the crystal. Often, the external object is so heavy that it does not take part in the MHz oscillation of the crystal due to inertia. It then rests in place in the laboratory frame. When the crystal surface is laterally displaced, the contact exerts a restoring force upon the crystal surface. The stress is proportional to the number density of the contacts, ''N''S, and their average spring constant, κS. The spring constant may be complex (κS* = κS’ + iκS’’), where the imaginary part quantifies a withdrawal of energy from the crystal oscillation (for instance due to viscoelastic effects). For such a situation, the small-load approximation predicts The QCM allows for non-destructive testing of the shear stiffness of multi-asperity contacts.See also
*Sauerbrey equation
The Sauerbrey equation was developed by the German Günter Sauerbrey in 1959, while working on his doctoral thesis at the Technical University of Berlin, Germany. It is a method for correlating changes in the oscillation frequency of a piezoelec ...
* Sauerbrey constant
* Sauerbrey layer
* Weighing scale
A scale or balance is a device used to measure weight or mass. These are also known as mass scales, weight scales, mass balances, and weight balances.
The traditional scale consists of two plates or bowls suspended at equal distances from a ...
* Piezoelectricity
Piezoelectricity (, ) is the electric charge that accumulates in certain solid materials—such as crystals, certain ceramics, and biological matter such as bone, DNA, and various proteins—in response to applied mechanical stress. The word ''p ...
* Thin-film thickness monitor Thin-film thickness monitors, deposition rate controllers, and so on, are a family of instruments used in high and ultra-high vacuum systems. They can measure the thickness of a thin film, not only after it has been made, but while it is still bei ...
* Quartz crystal microbalance with dissipation monitoring (QCM-D)
* Tapered element oscillating microbalance A tapered element oscillating microbalance (TEOM) is an instrument used for real-time detection of aerosol particles by measuring their mass concentration. It makes use of a small vibrating glass tube whose oscillation frequency changes when aeroso ...
(TEOM)
Notes
References
Further reading
* Quartz Crystal Microbalance with Dissipation monitoringWhat is QCM and how does it work?
* * * {{Webarchive , url=https://archive.today/20130106005935/http://www.pc.tu-clausthal.de/en/forschung/ak-johannsmann/qcm-modellierung/ , date=January 6, 2013 , title=Tutorial on modelling the behavior of the QCM
The Principles of QCM-I with impedance analysis and dissipation monitoring (QCM-D)
External links
QCM mini-FAQ
Weighing instruments