Quantum refrigerators on:
[Wikipedia]
[Google]
[Amazon]
A quantum heat engine is a device that generates power from the heat flow between hot and cold reservoirs.
The operation mechanism of the engine can be described by the laws of quantum mechanics.
The first realization of a quantum heat engine was pointed out by Scovil and Schulz-DuBois in 1959, showing the connection of efficiency of the Carnot engine and the 3-level maser.
Quantum
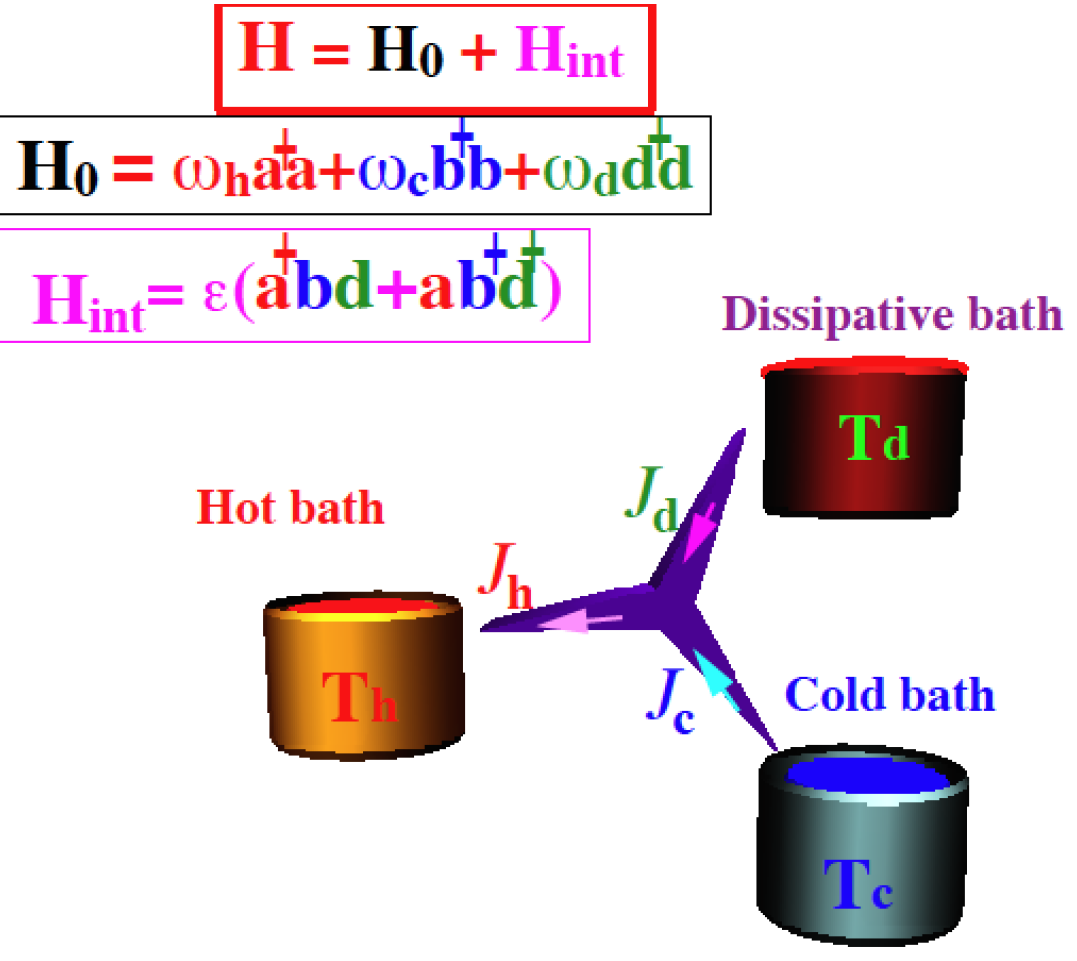 The tricycle engine has a generic structure.
The basic model consists of three thermal baths: A hot bath with temperature ,
a cold bath with temperature
and a work bath with temperature .
Each bath is connected to the engine via a frequency filter which can be modeled by three oscillators:
::
where , and
are the filter frequencies on resonance .
The device operates as a refrigerator by removing an excitation from the cold bath as well as from the work bath
and generating an excitation in the hot bath. The term in the Hamiltonian is non linear
and crucial for an engine or a refrigerator.
::
where is the coupling strength.
The first-law of thermodynamics represents the energy balance of heat currents originating from the three baths and collimating on the system:
::
At steady state no heat is accumulated in the tricycle, thus .
In addition, in steady state the entropy is only generated in the baths, leading to the second law of thermodynamics:
::
This version of the second-law is a generalisation of the statement of Clausius theorem;
heat does not flow spontaneously from cold to hot bodies.
When the temperature , no entropy is generated in the power bath.
An energy current with no accompanying entropy production is equivalent to generating pure power:
, where is the power output.
The tricycle engine has a generic structure.
The basic model consists of three thermal baths: A hot bath with temperature ,
a cold bath with temperature
and a work bath with temperature .
Each bath is connected to the engine via a frequency filter which can be modeled by three oscillators:
::
where , and
are the filter frequencies on resonance .
The device operates as a refrigerator by removing an excitation from the cold bath as well as from the work bath
and generating an excitation in the hot bath. The term in the Hamiltonian is non linear
and crucial for an engine or a refrigerator.
::
where is the coupling strength.
The first-law of thermodynamics represents the energy balance of heat currents originating from the three baths and collimating on the system:
::
At steady state no heat is accumulated in the tricycle, thus .
In addition, in steady state the entropy is only generated in the baths, leading to the second law of thermodynamics:
::
This version of the second-law is a generalisation of the statement of Clausius theorem;
heat does not flow spontaneously from cold to hot bodies.
When the temperature , no entropy is generated in the power bath.
An energy current with no accompanying entropy production is equivalent to generating pure power:
, where is the power output.
refrigerator
A refrigerator, colloquially fridge, is a commercial and home appliance consisting of a thermally insulated compartment and a heat pump (mechanical, electronic or chemical) that transfers heat from its inside to its external environment so th ...
s share the structure of quantum heat engines with the purpose of pumping heat from a cold to a hot bath consuming power
first suggested by Geusic, Schulz-DuBois, De Grasse and Scovil. When the power is supplied by a laser the process is termed optical pumping
Optical pumping is a process in which light is used to raise (or "pump") electrons from a lower energy level in an atom or molecule to a higher one. It is commonly used in laser construction to pump the active laser medium so as to achieve populat ...
or laser cooling, suggested by Wineland and Hänsch.D. J. Wineland and H. Dehmelt, Bull. Am. Phys. Soc. 20, 637 (1975)
Surprisingly heat engines and refrigerator
A refrigerator, colloquially fridge, is a commercial and home appliance consisting of a thermally insulated compartment and a heat pump (mechanical, electronic or chemical) that transfers heat from its inside to its external environment so th ...
s can operate up to the scale of a single particle thus justifying the need for a quantum theory termed quantum thermodynamics.
The 3-level amplifier as a quantum heat engine
The three-level-amplifier is the template of a quantum device. It operates by employing a hot and cold bath to maintainpopulation inversion
In science, specifically statistical mechanics, a population inversion occurs while a system (such as a group of atoms or molecules) exists in a state in which more members of the system are in higher, excited states than in lower, unexcited energ ...
between two energy levels which is used to amplify light by stimulated emission
Stimulated emission is the process by which an incoming photon of a specific frequency can interact with an excited atomic electron (or other excited molecular state), causing it to drop to a lower energy level. The liberated energy transfers to th ...
The ground state level (1-g) and the excited level (3-h) are coupled to a hot bath of temperature .
The energy gap is . When the population on the levels equilibrate
::
where is the Planck constant and is the Boltzmann constant.
The cold bath of temperature couples the ground (1-g) to an intermediate level (2-c)
with energy gap .
When levels 2-c and 1-g equilibrate then
::.
The device operates as an amplifier when levels (3-h) and (2-c) are coupled to an external field of frequency .
For optimal resonance conditions .
The efficiency of the amplifier in converting heat to power is the ratio of work output to heat input:
::.
Amplification of the field is possible only for positive gain (population inversion)
.
This is equivalent to .
Inserting this expression into the efficiency formula leads to:
::
where is the Carnot cycle efficiency
Efficiency is the often measurable ability to avoid wasting materials, energy, efforts, money, and time in doing something or in producing a desired result. In a more general sense, it is the ability to do things well, successfully, and without ...
.
Equality is obtained under a zero gain condition .
The relation between the quantum amplifier and the Carnot efficiency was first pointed out by Scovil and Schultz-DuBois:
Reversing the operation driving heat from the cold bath to the hot bath by consuming power constitutes a refrigerator
A refrigerator, colloquially fridge, is a commercial and home appliance consisting of a thermally insulated compartment and a heat pump (mechanical, electronic or chemical) that transfers heat from its inside to its external environment so th ...
.
The efficiency of the refrigerator defined as the coefficient of performance (COP) for the reversed device is:
::
Types
Quantum devices can operate either continuously or by a reciprocating cycle. Continuous devices include solar cells converting solar radiation to electrical power,thermoelectric
The thermoelectric effect is the direct conversion of temperature differences to electric voltage and vice versa via a thermocouple. A thermoelectric device creates a voltage when there is a different temperature on each side. Conversely, when ...
where the output is current and lasers where the output power is coherent light.
The primary example of a continuous refrigerator is optical pumping
Optical pumping is a process in which light is used to raise (or "pump") electrons from a lower energy level in an atom or molecule to a higher one. It is commonly used in laser construction to pump the active laser medium so as to achieve populat ...
and laser cooling.
Similarly to classical reciprocating engines, quantum heat engines also have a cycle that is divided into different strokes. A stroke is time segment in which a certain operation takes place (e.g. thermalization, or work extraction). Two adjacent strokes do not commute with each other. The most common reciprocating heat machines are the four-stroke machine, and the two-stroke machine. Reciprocating devices have been suggested operating either by the Carnot cycle or the Otto cycle.
In both types the quantum description allows to obtain equation of motion for the working medium
and the heat flow from the reservoirs.
Quantum reciprocating heat engine and refrigerator
Quantum versions of most of the common thermodynamic cycles have been studied, for example the Carnot cycle,Stirling cycle
The Stirling cycle is a thermodynamic cycle that describes the general class of Stirling devices. This includes the original Stirling engine that was invented, developed and patented in 1816 by Robert Stirling with help from his brother, an en ...
and Otto cycle.
The Otto cycle can serve as a template for other reciprocating cycles.
It is composed of the following four segments:
*Segment ''isomagnetic'' or '' isochoric process'', partial equilibration with the cold bath under constant Hamiltonian. The dynamics of the working medium is characterized by the propagator .
*Segment ''magnetization
In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Movement within this field is described by direction and is either Axial or Di ...
'' or adiabatic compression, the external field changes expanding the gap between energy levels of the Hamiltonian. The dynamics is characterized by the propagator .
*Segment ''isomagnetic'', or ''isochoric process'' partial equilibration with the hot bath described by the propagator .
*Segment ''demagnetization
In classical electromagnetism, magnetization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material. Movement within this field is described by direction and is either Axial or Di ...
'' or adiabatic expansion reducing the energy gaps in the Hamiltonian, characterized by the propagator .
The propagator of the four stroke cycle
becomes , which is the ordered product of the segment propagators:
::
The propagators are linear operators defined on a vector space which completely determines the state of the working medium.
Common to all thermodynamic cycles the consecutive segment propagators do not commute .
Commuting propagators will lead to zero power.
In a reciprocating quantum heat engine the working medium is a quantum system such as spin systems or an harmonic oscillator. For maximum power the cycle time should be optimized.
There are two basic timescales in the reciprocating refrigerator the cycle time and the internal
timescale . In general when the
engine operates in quasi-adiabatic conditions. The only quantum effect can be found at low temperatures
where the unit of energy of the device becomes instead of .
The efficiency at this limit is , always smaller than the Carnot efficiency
A Carnot cycle is an ideal thermodynamic cycle proposed by French physicist Sadi Carnot in 1824 and expanded upon by others in the 1830s and 1840s. By Carnot's theorem, it provides an upper limit on the efficiency of any classical thermodynam ...
. At high temperature and for the harmonic working medium the efficiency at maximum power becomes which is the endoreversible thermodynamics
Endoreversible thermodynamics is a subset of irreversible thermodynamics aimed at making more realistic assumptions about heat transfer than are typically made in reversible thermodynamics. It gives an upper bound on the energy that can be derive ...
result.
For shorter cycle times the working medium cannot follow adiabatically the change in the external parameter.
This leads to friction-like phenomena. Extra power is required to drive the system faster.
The signature of such dynamics is the development of coherence causing extra dissipation.
Surprisingly the dynamics leading to friction is quantized meaning that frictionless solutions to the adiabatic expansion/compression
can be found in finite time.
As a result, optimization has to be carried out only with respect to the time allocated
to heat transport. In this regime the quantum feature of coherence degrades the performance.
Optimal frictionless performance is obtained when the coherence can be cancelled.
The shortest cycle times , sometimes termed sudden cycles, have universal features. In this case coherence contributes to the cycles power.
A two-stroke engine quantum cycle equivalent to the Otto cycle based on two qubits has been proposed.
The first qubit has frequency and the second . The cycle is composed
of a first stroke of partial equilibration of the two qubits with the hot and cold bath in parallel.
The second power stroke is composed of a partial or full swap between the qubits.
The swap operation is generated by a unitary transformation which preserves the entropy
as a result it is a pure power stroke.
The quantum Otto cycle refrigerators shares the same cycle with magnetic refrigeration
Magnetic refrigeration is a cooling technology based on the magnetocaloric effect. This technique can be used to attain extremely low temperatures, as well as the ranges used in common refrigerators.
A magnetocaloric material warms up when a m ...
.
Continuous quantum engines
Continuous quantum engines are the quantum analogues of turbines. The work output mechanism is coupling to an external periodic field, typically the electromagnetic field. Thus the heat engine is a model for a laser. The models differ by the choice of their working substance and heat source and sink. Externally driven two-level, three level four-level and coupled harmonic oscillators have been studied. The periodic driving splits the energy level structure of the working medium. This splitting allows the two level engine to couple selectively to the hot and cold baths and produce power. On the other hand, ignoring this splitting in the derivation of the equation of motion will violate the second law of thermodynamics. Non thermal fuels have been considered for quantum heat engines. The idea is to increase the energy content of the hot bath without increasing its entropy. This can be achieved by employing coherence or a squeezed thermal bath. These devices do not violate the second law of thermodynamics.Equivalence of reciprocating and continuous heat machines in the quantum regime
Two-stroke, Four-stroke, and continuous machine are very different from each other. However it was shown that there is a quantum regime where all these machines become thermodynamically equivalent to each other. While the intra cycle dynamics in the equivalence regime is very different in different engine types, when the cycle is completed they all turn out to provide the same amount of work and consume the same amount of heat (hence they share the same efficiency as well). This equivalence is associated with a coherent work extraction mechanism and has no classical analogue. These quantum features have been demonstrated experimentally.Heat engines and open quantum systems
The elementary example operates under quasi equilibrium conditions. Its main quantum feature is the discrete energy level structure. More realistic devices operate out of equilibrium possessing friction heat leaks and finite heat flow. Quantum thermodynamics supplies a dynamical theory required for systems out of equilibrium such as heat engines, thus, inserting dynamics into thermodynamics. The theory ofopen quantum system In physics, an open quantum system is a quantum-mechanical system that interacts with an external quantum system, which is known as the ''environment'' or a ''bath''. In general, these interactions significantly change the dynamics of the system an ...
s constitutes the basic theory. For heat engines a reduced description of the dynamics
of the working substance is sought, tracing out the hot and cold baths.
The starting point is the general Hamiltonian of the combined systems:
::
and the system Hamiltonian is time dependent.
A reduced description leads to the equation of motion of the system:
::
where is the density operator describing the state of the working medium and is the generator of dissipative dynamics
which includes the heat transport terms from the baths.
Using this construction, the total change in energy of the sub-system becomes:
::
leading to the dynamical version of the first law of thermodynamics:
* The power
* Heat currents and .
The rate of entropy production becomes:
::
The global structure of quantum mechanics is reflected in the derivation of the reduced description.
A derivation which is consistent with the laws of thermodynamics is based on
the weak coupling limit.
A thermodynamical idealization assumes that the system and the baths are uncorrelated, meaning that the total state
of the combined system becomes a tensor product at all times:
::
Under these conditions the dynamical equations of motion become:
where is the Liouville superoperator described in terms of the system's Hilbert space,
where the reservoirs are described implicitly.
Within the formalism of quantum open system, can take the form of the
Gorini-Kossakowski-Sudarshan-Lindblad (GKS-L) Markovian generator or also known just as Lindblad equation
. Theories beyond the weak coupling regime have been proposed.
The quantum absorption refrigerator
The absorption refrigerator is of unique importance in setting an autonomous quantum device. Such a device requires no external power and operates without external intervention in scheduling the operations . The basic construct includes three baths; a power bath, a hot bath and a cold bath. The tricycle model is the template for the absorption refrigerator. The tricycle engine has a generic structure.
The basic model consists of three thermal baths: A hot bath with temperature ,
a cold bath with temperature
and a work bath with temperature .
Each bath is connected to the engine via a frequency filter which can be modeled by three oscillators:
::
where , and
are the filter frequencies on resonance .
The device operates as a refrigerator by removing an excitation from the cold bath as well as from the work bath
and generating an excitation in the hot bath. The term in the Hamiltonian is non linear
and crucial for an engine or a refrigerator.
::
where is the coupling strength.
The first-law of thermodynamics represents the energy balance of heat currents originating from the three baths and collimating on the system:
::
At steady state no heat is accumulated in the tricycle, thus .
In addition, in steady state the entropy is only generated in the baths, leading to the second law of thermodynamics:
::
This version of the second-law is a generalisation of the statement of Clausius theorem;
heat does not flow spontaneously from cold to hot bodies.
When the temperature , no entropy is generated in the power bath.
An energy current with no accompanying entropy production is equivalent to generating pure power:
, where is the power output.
The tricycle engine has a generic structure.
The basic model consists of three thermal baths: A hot bath with temperature ,
a cold bath with temperature
and a work bath with temperature .
Each bath is connected to the engine via a frequency filter which can be modeled by three oscillators:
::
where , and
are the filter frequencies on resonance .
The device operates as a refrigerator by removing an excitation from the cold bath as well as from the work bath
and generating an excitation in the hot bath. The term in the Hamiltonian is non linear
and crucial for an engine or a refrigerator.
::
where is the coupling strength.
The first-law of thermodynamics represents the energy balance of heat currents originating from the three baths and collimating on the system:
::
At steady state no heat is accumulated in the tricycle, thus .
In addition, in steady state the entropy is only generated in the baths, leading to the second law of thermodynamics:
::
This version of the second-law is a generalisation of the statement of Clausius theorem;
heat does not flow spontaneously from cold to hot bodies.
When the temperature , no entropy is generated in the power bath.
An energy current with no accompanying entropy production is equivalent to generating pure power:
, where is the power output.
Quantum refrigerators and the third law of thermodynamics
There are seemingly two independent formulations of the third law of thermodynamics both originally were stated byWalther Nernst
Walther Hermann Nernst (; 25 June 1864 – 18 November 1941) was a German chemist known for his work in thermodynamics, physical chemistry, electrochemistry, and solid state physics. His formulation of the Nernst heat theorem helped pave the wa ...
. The first formulation is known as the Nernst heat theorem
The Nernst heat theorem was formulated by Walther Nernst early in the twentieth century and was used in the development of the third law of thermodynamics.
The theorem
The Nernst heat theorem says that as absolute zero is approached, the entropy ...
, and can be phrased as:
*The entropy of any pure substance in thermodynamic equilibrium approaches zero as the temperature approaches zero.
The second formulation is dynamical, known as the ''unattainability principle'':
*It is impossible by any procedure, no matter how idealized, to reduce any assembly to absolute zero
Absolute zero is the lowest limit of the thermodynamic temperature scale, a state at which the enthalpy and entropy of a cooled ideal gas reach their minimum value, taken as zero kelvin. The fundamental particles of nature have minimum vibration ...
temperature in a finite number of operations.
At steady state the second law of thermodynamics implies that the total entropy production is non-negative.
When the cold bath approaches the absolute zero temperature,
it is necessary to eliminate the entropy production divergence at the cold side
when , therefore
::
For the fulfillment of the second law depends on the entropy production of the other baths,
which should compensate for the negative entropy production of the cold bath.
The first formulation of the third law modifies this restriction.
Instead of the third law imposes ,
guaranteeing that at absolute zero the entropy production at the cold bath is zero: .
This requirement leads to the scaling condition of the heat current .
The second formulation, known as the unattainability principle can be rephrased as;
*No refrigerator can cool a system to absolute zero
Absolute zero is the lowest limit of the thermodynamic temperature scale, a state at which the enthalpy and entropy of a cooled ideal gas reach their minimum value, taken as zero kelvin. The fundamental particles of nature have minimum vibration ...
temperature at finite time.
The dynamics of the cooling process is governed by the equation
::
where is the heat capacity of the bath. Taking and with , we can quantify this formulation by evaluating the characteristic exponent of the cooling process,
::
This equation introduce the relation between the characteristic exponents and . When then the bath is cooled to zero temperature in a finite time, which implies a violation of the third law. It is apparent from the last equation, that the unattainability principle is more restrictive than the Nernst heat theorem
The Nernst heat theorem was formulated by Walther Nernst early in the twentieth century and was used in the development of the third law of thermodynamics.
The theorem
The Nernst heat theorem says that as absolute zero is approached, the entropy ...
.
References
Further reading
Deffner, Sebastian and Campbell, Steve. "Quantum Thermodynamics: An introduction to the thermodynamics of quantum information", (Morgan & Claypool Publishers, 2019). F. Binder, L. A. Correa, C. Gogolin, J. Anders, G. Adesso (eds.) "Thermodynamics in the Quantum Regime. Fundamental Aspects and New Directions." (Springer 2018) Gemmer, Jochen, M. Michel, and Günter Mahler. "Quantum thermodynamics. Emergence of thermodynamic behavior within composite quantum systems. 2." (2009). Petruccione, Francesco, and Heinz-Peter Breuer. The theory of open quantum systems. Oxford university press, 2002.External links
*{{cite web , url=http://phys.org/news/2014-01-nanoscale-standard-efficiency-limit.html , title=Nanoscale heat engine exceeds standard efficiency limit , website=phys.org Quantum mechanics Heat pumps Thermodynamics