Quantum neural network on:
[Wikipedia]
[Google]
[Amazon]
 Quantum neural networks are computational neural network models which are based on the principles of
Quantum neural networks are computational neural network models which are based on the principles of
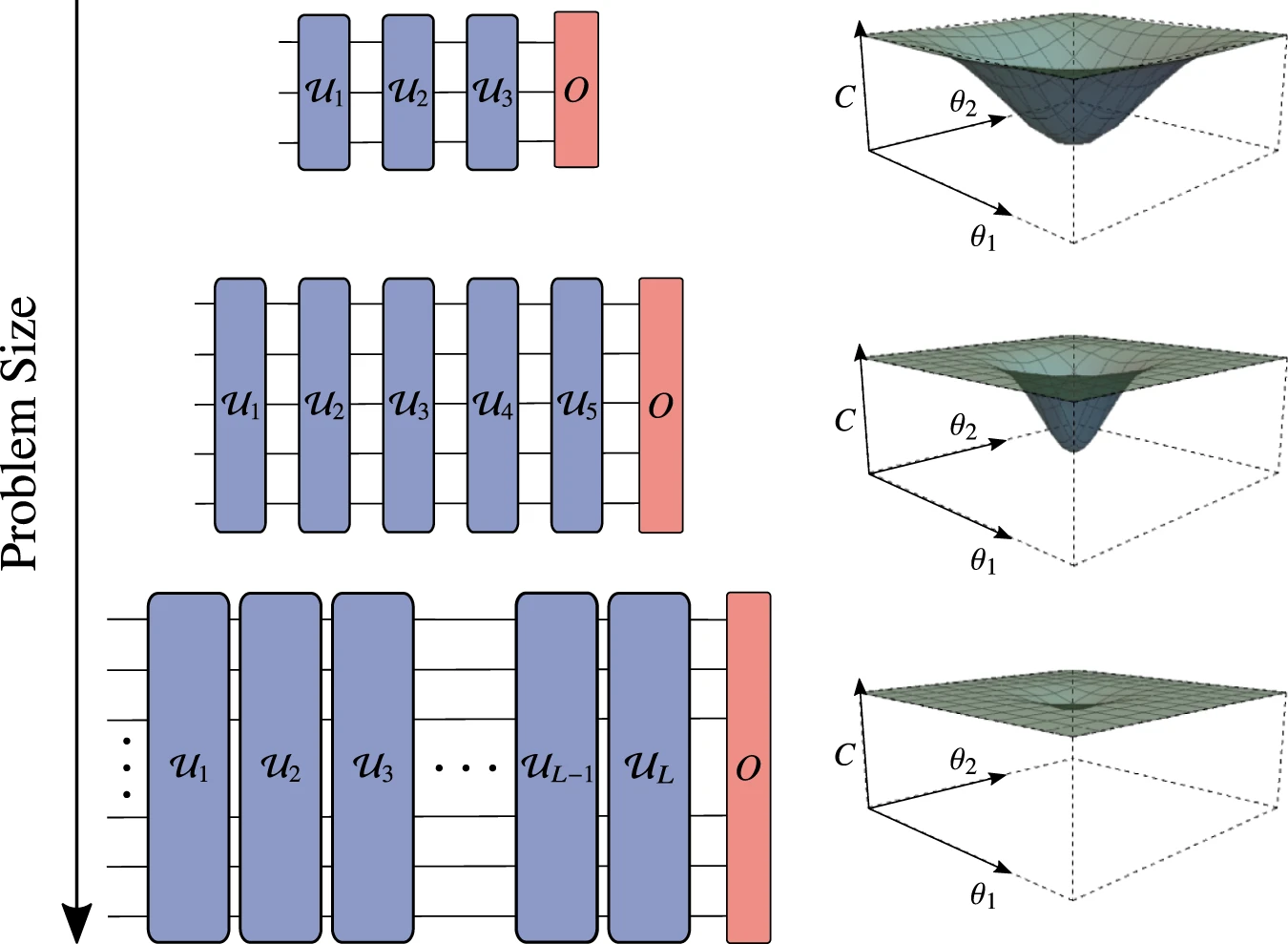 Gradient descent is widely used and successful in classical algorithms. However, although the simplified structure is very similar to neural networks such as CNNs, QNNs perform much worse.
Since the quantum space exponentially expands as the q-bit grows, the observations will concentrate around the mean value at an exponential rate, where also have exponentially small gradients.
This situation is known as Barren Plateaus, because most of the initial parameters are trapped on a "plateau" of almost zero gradient, which approximates random wandering rather than gradient descent. This makes the model untrainable.
In fact, not only QNN, but almost all deeper VQA algorithms have this problem. In the present NISQ era, this is one of the problems that have to be solved if more applications are to be made of the various VQA algorithms, including QNN.
Gradient descent is widely used and successful in classical algorithms. However, although the simplified structure is very similar to neural networks such as CNNs, QNNs perform much worse.
Since the quantum space exponentially expands as the q-bit grows, the observations will concentrate around the mean value at an exponential rate, where also have exponentially small gradients.
This situation is known as Barren Plateaus, because most of the initial parameters are trapped on a "plateau" of almost zero gradient, which approximates random wandering rather than gradient descent. This makes the model untrainable.
In fact, not only QNN, but almost all deeper VQA algorithms have this problem. In the present NISQ era, this is one of the problems that have to be solved if more applications are to be made of the various VQA algorithms, including QNN.
Recent review of quantum neural networks by M. Schuld, I. Sinayskiy and F. Petruccione
Article by P. Gralewicz on the plausibility of quantum computing in biological neural networks
{{emerging technologies, quantum=yes, other=yes Artificial neural networks Quantum information science Quantum programming
 Quantum neural networks are computational neural network models which are based on the principles of
Quantum neural networks are computational neural network models which are based on the principles of quantum mechanics
Quantum mechanics is the fundamental physical Scientific theory, theory that describes the behavior of matter and of light; its unusual characteristics typically occur at and below the scale of atoms. Reprinted, Addison-Wesley, 1989, It is ...
. The first ideas on quantum neural computation were published independently in 1995 by Subhash Kak and Ron Chrisley, engaging with the theory of quantum mind, which posits that quantum effects play a role in cognitive function. However, typical research in quantum neural networks involves combining classical artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
models (which are widely used in machine learning for the important task of pattern recognition) with the advantages of quantum information in order to develop more efficient algorithms. One important motivation for these investigations is the difficulty to train classical neural networks, especially in big data applications. The hope is that features of quantum computing
A quantum computer is a computer that exploits quantum mechanical phenomena. On small scales, physical matter exhibits properties of wave-particle duality, both particles and waves, and quantum computing takes advantage of this behavior using s ...
such as quantum parallelism or the effects of interference
Interference is the act of interfering, invading, or poaching. Interference may also refer to:
Communications
* Interference (communication), anything which alters, modifies, or disrupts a message
* Adjacent-channel interference, caused by extra ...
and entanglement can be used as resources. Since the technological implementation of a quantum computer is still in a premature stage, such quantum neural network models are mostly theoretical proposals that await their full implementation in physical experiments.
Most Quantum neural networks are developed as feed-forward networks. Similar to their classical counterparts, this structure intakes input from one layer of qubits, and passes that input onto another layer of qubits. This layer of qubits evaluates this information and passes on the output to the next layer. Eventually the path leads to the final layer of qubits. The layers do not have to be of the same width, meaning they don't have to have the same number of qubits as the layer before or after it. This structure is trained on which path to take similar to classical artificial neural network
In machine learning, a neural network (also artificial neural network or neural net, abbreviated ANN or NN) is a computational model inspired by the structure and functions of biological neural networks.
A neural network consists of connected ...
s. This is discussed in a lower section. Quantum neural networks refer to three different categories: Quantum computer with classical data, classical computer with quantum data, and quantum computer with quantum data.
Examples
Quantum neural network research is still in its infancy, and a conglomeration of proposals and ideas of varying scope and mathematical rigor have been put forward. Most of them are based on the idea of replacing classical binary orMcCulloch-Pitts neuron
An artificial neuron is a mathematical function conceived as a model of a biological neuron in a neural network. The artificial neuron is the elementary unit of an ''artificial neural network''.
The design of the artificial neuron was inspired ...
s with a qubit
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical syste ...
(which can be called a “quron”), resulting in neural units that can be in a superposition
In mathematics, a linear combination or superposition is an expression constructed from a set of terms by multiplying each term by a constant and adding the results (e.g. a linear combination of ''x'' and ''y'' would be any expression of the form ...
of the state ‘firing’ and ‘resting’.
Quantum perceptrons
A lot of proposals attempt to find a quantum equivalent for theperceptron
In machine learning, the perceptron is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function that can decide whether or not an input, represented by a vect ...
unit from which neural nets are constructed. A problem is that nonlinear activation functions do not immediately correspond to the mathematical structure of quantum theory, since a quantum evolution is described by linear operations and leads to probabilistic observation. Ideas to imitate the perceptron activation function with a quantum mechanical formalism reach from special measurements to postulating non-linear quantum operators (a mathematical framework that is disputed). A direct implementation of the activation function using the circuit-based model of quantum computation has recently been proposed by Schuld, Sinayskiy and Petruccione based on the quantum phase estimation algorithm
In quantum computing, the quantum phase estimation algorithm is a quantum algorithm to estimate the phase corresponding to an eigenvalue of a given unitary operator. Because the eigenvalues of a unitary operator always have unit modulus, they a ...
.
Quantum networks
At a larger scale, researchers have attempted to generalize neural networks to the quantum setting. One way of constructing a quantum neuron is to first generalise classical neurons and then generalising them further to make unitary gates. Interactions between neurons can be controlled quantumly, withunitary
Unitary may refer to:
Mathematics
* Unitary divisor
* Unitary element
* Unitary group
* Unitary matrix
* Unitary morphism
* Unitary operator
* Unitary transformation
* Unitary representation
* Unitarity (physics)
* ''E''-unitary inverse semigr ...
gates, or classically, via measurement
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared to ...
of the network states. This high-level theoretical technique can be applied broadly, by taking different types of networks and different implementations of quantum neurons, such as photonically implemented neurons and quantum reservoir processor (quantum version of reservoir computing). Most learning algorithms follow the classical model of training an artificial neural network to learn the input-output function of a given training set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from ...
and use classical feedback loops to update parameters of the quantum system until they converge to an optimal configuration. Learning as a parameter optimisation problem has also been approached by adiabatic models of quantum computing.
Quantum neural networks can be applied to algorithmic design: given qubits
In quantum computing, a qubit () or quantum bit is a basic unit of quantum information—the quantum version of the classic binary bit physically realized with a two-state device. A qubit is a two-state (or two-level) quantum-mechanical system, ...
with tunable mutual interactions, one can attempt to learn interactions following the classical backpropagation
In machine learning, backpropagation is a gradient computation method commonly used for training a neural network to compute its parameter updates.
It is an efficient application of the chain rule to neural networks. Backpropagation computes th ...
rule from a training set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from ...
of desired input-output relations, taken to be the desired output algorithm's behavior. The quantum network thus ‘learns’ an algorithm.
Quantum associative memory
The first quantum associative memory algorithm was introduced by Dan Ventura and Tony Martinez in 1999. The authors do not attempt to translate the structure of artificial neural network models into quantum theory, but propose an algorithm for a circuit-based quantum computer that simulates associative memory. The memory states (in Hopfield neural networks saved in the weights of the neural connections) are written into a superposition, and a Grover-like quantum search algorithm retrieves the memory state closest to a given input. As such, this is not a fully content-addressable memory, since only incomplete patterns can be retrieved. The first truly content-addressable quantum memory, which can retrieve patterns also from corrupted inputs, was proposed by Carlo A. Trugenberger. Both memories can store an exponential (in terms of n qubits) number of patterns but can be used only once due to the no-cloning theorem and their destruction upon measurement. Trugenberger, however, has shown that his probabilistic model of quantum associative memory can be efficiently implemented and re-used multiples times for any polynomial number of stored patterns, a large advantage with respect to classical associative memories.Classical neural networks inspired by quantum theory
A substantial amount of interest has been given to a “quantum-inspired” model that uses ideas from quantum theory to implement a neural network based onfuzzy logic
Fuzzy logic is a form of many-valued logic in which the truth value of variables may be any real number between 0 and 1. It is employed to handle the concept of partial truth, where the truth value may range between completely true and completely ...
.
Training
Quantum Neural Networks can be theoretically trained similarly to training classical/artificial neural networks. A key difference lies in communication between the layers of a neural networks. For classical neural networks, at the end of a given operation, the currentperceptron
In machine learning, the perceptron is an algorithm for supervised classification, supervised learning of binary classification, binary classifiers. A binary classifier is a function that can decide whether or not an input, represented by a vect ...
copies its output to the next layer of perceptron(s) in the network. However, in a quantum neural network, where each perceptron is a qubit, this would violate the no-cloning theorem
In physics, the no-cloning theorem states that it is impossible to create an independent and identical copy of an arbitrary unknown quantum state, a statement which has profound implications in the field of quantum computer, quantum computing among ...
. A proposed generalized solution to this is to replace the classical fan-out
In digital electronics, the fan-out is the number of gate inputs driven by the output of another single logic gate.
In most designs, logic gates are connected to form more complex circuits. While no logic gate input can be fed by more than one ...
method with an arbitrary unitary
Unitary may refer to:
Mathematics
* Unitary divisor
* Unitary element
* Unitary group
* Unitary matrix
* Unitary morphism
* Unitary operator
* Unitary transformation
* Unitary representation
* Unitarity (physics)
* ''E''-unitary inverse semigr ...
that spreads out, but does not copy, the output of one qubit to the next layer of qubits. Using this fan-out Unitary () with a dummy state qubit in a known state (Ex. in the computational basis), also known as an Ancilla bit, the information from the qubit can be transferred to the next layer of qubits. This process adheres to the quantum operation requirement of reversibility.
Using this quantum feed-forward network, deep neural networks can be executed and trained efficiently. A deep neural network is essentially a network with many hidden-layers, as seen in the sample model neural network above. Since the Quantum neural network being discussed uses fan-out Unitary operators, and each operator only acts on its respective input, only two layers are used at any given time. In other words, no Unitary operator is acting on the entire network at any given time, meaning the number of qubits required for a given step depends on the number of inputs in a given layer. Since Quantum Computers are notorious for their ability to run multiple iterations in a short period of time, the efficiency of a quantum neural network is solely dependent on the number of qubits in any given layer, and not on the depth of the network.
Cost functions
To determine the effectiveness of a neural network, a cost function is used, which essentially measures the proximity of the network's output to the expected or desired output. In a Classical Neural Network, the weights () and biases () at each step determine the outcome of the cost function . When training a Classical Neural network, the weights and biases are adjusted after each iteration, and given equation 1 below, where is the desired output and is the actual output, the cost function is optimized when = 0. For a quantum neural network, the cost function is determined by measuring the fidelity of the outcome state () with the desired outcome state (), seen in Equation 2 below. In this case, the Unitary operators are adjusted after each iteration, and the cost function is optimized when C = 1. Equation 1 Equation 2Barren plateaus
 Gradient descent is widely used and successful in classical algorithms. However, although the simplified structure is very similar to neural networks such as CNNs, QNNs perform much worse.
Since the quantum space exponentially expands as the q-bit grows, the observations will concentrate around the mean value at an exponential rate, where also have exponentially small gradients.
This situation is known as Barren Plateaus, because most of the initial parameters are trapped on a "plateau" of almost zero gradient, which approximates random wandering rather than gradient descent. This makes the model untrainable.
In fact, not only QNN, but almost all deeper VQA algorithms have this problem. In the present NISQ era, this is one of the problems that have to be solved if more applications are to be made of the various VQA algorithms, including QNN.
Gradient descent is widely used and successful in classical algorithms. However, although the simplified structure is very similar to neural networks such as CNNs, QNNs perform much worse.
Since the quantum space exponentially expands as the q-bit grows, the observations will concentrate around the mean value at an exponential rate, where also have exponentially small gradients.
This situation is known as Barren Plateaus, because most of the initial parameters are trapped on a "plateau" of almost zero gradient, which approximates random wandering rather than gradient descent. This makes the model untrainable.
In fact, not only QNN, but almost all deeper VQA algorithms have this problem. In the present NISQ era, this is one of the problems that have to be solved if more applications are to be made of the various VQA algorithms, including QNN.
See also
*Differentiable programming
Differentiable programming is a programming paradigm in which a numeric computer program can be differentiated throughout via automatic differentiation. This allows for gradient-based optimization of parameters in the program, often via gradient ...
* Optical neural network
* Holographic associative memory
* Quantum cognition
* Quantum machine learning
References
External links
Recent review of quantum neural networks by M. Schuld, I. Sinayskiy and F. Petruccione
Article by P. Gralewicz on the plausibility of quantum computing in biological neural networks
{{emerging technologies, quantum=yes, other=yes Artificial neural networks Quantum information science Quantum programming