Probability distribution fitting on:
[Wikipedia]
[Google]
[Amazon]
Probability distribution fitting or simply distribution fitting is the fitting of a
 The selection of the appropriate distribution depends on the presence or absence of symmetry of the data set with respect to the central tendency.
''Symmetrical distributions''
When the data are symmetrically distributed around the mean while the frequency of occurrence of data farther away from the mean diminishes, one may for example select the normal distribution, the logistic distribution, or the
The selection of the appropriate distribution depends on the presence or absence of symmetry of the data set with respect to the central tendency.
''Symmetrical distributions''
When the data are symmetrically distributed around the mean while the frequency of occurrence of data farther away from the mean diminishes, one may for example select the normal distribution, the logistic distribution, or the  When the larger values tend to be farther away from the mean than the smaller values, one has a skew distribution to the right (i.e. there is positive skewness), one may for example select the log-normal distribution (i.e. the log values of the data are normally distributed), the log-logistic distribution (i.e. the log values of the data follow a logistic distribution), the Gumbel distribution, the
When the larger values tend to be farther away from the mean than the smaller values, one has a skew distribution to the right (i.e. there is positive skewness), one may for example select the log-normal distribution (i.e. the log values of the data are normally distributed), the log-logistic distribution (i.e. the log values of the data follow a logistic distribution), the Gumbel distribution, the
/ref> the inverted (mirrored) Gumbel distribution, the Dagum distribution (mirrored Burr distribution), or the Gompertz distribution, which is bounded to the left.
o
/ref> ::
/ref>
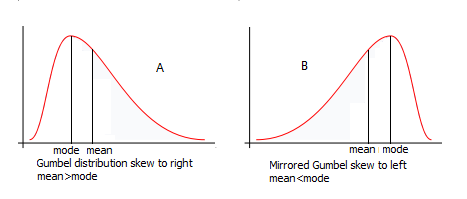 Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
The technique of distribution shifting augments the chance to find a properly fitting probability distribution.
 The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
 Predictions of occurrence based on fitted probability distributions are subject to uncertainty, which arises from the following conditions:
* The true probability distribution of events may deviate from the fitted distribution, as the observed data series may not be totally representative of the real probability of occurrence of the phenomenon due to random error
* The occurrence of events in another situation or in the future may deviate from the fitted distribution as this occurrence can also be subject to random error
* A change of environmental conditions may cause a change in the probability of occurrence of the phenomenon
An estimate of the uncertainty in the first and second case can be obtained with the binomial probability distribution using for example the probability of exceedance ''Pe'' (i.e. the chance that the event ''X'' is larger than a reference value ''Xr'' of ''X'') and the probability of non-exceedance ''Pn'' (i.e. the chance that the event ''X'' is smaller than or equal to the reference value ''Xr'', this is also called cumulative probability). In this case there are only two possibilities: either there is exceedance or there is non-exceedance. This duality is the reason that the binomial distribution is applicable.
With the binomial distribution one can obtain a prediction interval. Such an interval also estimates the risk of failure, i.e. the chance that the predicted event still remains outside the confidence interval. The confidence or risk analysis may include the return period ''T=1/Pe'' as is done in hydrology.
Predictions of occurrence based on fitted probability distributions are subject to uncertainty, which arises from the following conditions:
* The true probability distribution of events may deviate from the fitted distribution, as the observed data series may not be totally representative of the real probability of occurrence of the phenomenon due to random error
* The occurrence of events in another situation or in the future may deviate from the fitted distribution as this occurrence can also be subject to random error
* A change of environmental conditions may cause a change in the probability of occurrence of the phenomenon
An estimate of the uncertainty in the first and second case can be obtained with the binomial probability distribution using for example the probability of exceedance ''Pe'' (i.e. the chance that the event ''X'' is larger than a reference value ''Xr'' of ''X'') and the probability of non-exceedance ''Pn'' (i.e. the chance that the event ''X'' is smaller than or equal to the reference value ''Xr'', this is also called cumulative probability). In this case there are only two possibilities: either there is exceedance or there is non-exceedance. This duality is the reason that the binomial distribution is applicable.
With the binomial distribution one can obtain a prediction interval. Such an interval also estimates the risk of failure, i.e. the chance that the predicted event still remains outside the confidence interval. The confidence or risk analysis may include the return period ''T=1/Pe'' as is done in hydrology.

probability distribution
In probability theory and statistics, a probability distribution is the mathematical function that gives the probabilities of occurrence of different possible outcomes for an experiment. It is a mathematical description of a random phenomenon i ...
to a series of data concerning the repeated measurement of a variable phenomenon.
The aim of distribution fitting is to predict the probability or to forecast the frequency of occurrence of the magnitude of the phenomenon in a certain interval.
There are many probability distributions (see list of probability distributions) of which some can be fitted more closely to the observed frequency of the data than others, depending on the characteristics of the phenomenon and of the distribution. The distribution giving a close fit is supposed to lead to good predictions.
In distribution fitting, therefore, one needs to select a distribution that suits the data well.
Selection of distribution
Student's t-distribution
In probability and statistics, Student's ''t''-distribution (or simply the ''t''-distribution) is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in sit ...
. The first two are very similar, while the last, with one degree of freedom, has "heavier tails" meaning that the values farther away from the mean occur relatively more often (i.e. the kurtosis is higher). The Cauchy distribution is also symmetric.
''Skew distributions to the right''
exponential distribution
In probability theory and statistics, the exponential distribution is the probability distribution of the time between events in a Poisson point process, i.e., a process in which events occur continuously and independently at a constant average ...
, the Pareto distribution
The Pareto distribution, named after the Italian civil engineer, economist, and sociologist Vilfredo Pareto ( ), is a power-law probability distribution that is used in description of social, quality control, scientific, geophysical, actua ...
, the Weibull distribution, the Burr distribution, or the Fréchet distribution. The last four distributions are bounded to the left.
''Skew distributions to the left''
When the smaller values tend to be farther away from the mean than the larger values, one has a skew distribution to the left (i.e. there is negative skewness), one may for example select the ''square-normal distribution'' (i.e. the normal distribution applied to the square of the data values),Left (negatively) skewed frequency histograms can be fitted to square Normal or mirrored Gumbel probability functions. On line/ref> the inverted (mirrored) Gumbel distribution, the Dagum distribution (mirrored Burr distribution), or the Gompertz distribution, which is bounded to the left.
Techniques of fitting
The following techniques of distribution fitting exist: *''Parametric methods'', by which the parameters of the distribution are calculated from the data series. The parametric methods are: ** Method of moments ** Maximum spacing estimation **Method of L-moments ** Maximum likelihood method :: * Plotting position plus Regression analysis, using a transformation of thecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
so that a linear relation is found between the cumulative probability and the values of the data, which may also need to be transformed, depending on the selected probability distribution. In this method the cumulative probability needs to be estimated by the plotting positionSoftware for Generalized and Composite Probability Distributions. International Journal of Mathematical and Computational Methods, 4, 1-o
/ref> ::
Generalization of distributions
It is customary to transform data logarithmically to fit symmetrical distributions (like the normal distribution, normal and logistic) to data obeying a distribution that is positively skewed (i.e. skew to the right, with mean > mode, and with a right hand tail that is longer than the left hand tail), see lognormal distribution and theloglogistic distribution
In probability and statistics, the log-logistic distribution (known as the Fisk distribution in economics) is a continuous probability distribution for a non-negative random variable. It is used in survival analysis as a parametric model for events ...
. A similar effect can be achieved by taking the square root of the data.
To fit a symmetrical distribution to data obeying a negatively skewed distribution (i.e. skewed to the left, with mean < mode, and with a right hand tail this is shorter than the left hand tail) one could use the squared values of the data to accomplish the fit.
More generally one can raise the data to a power ''p'' in order to fit symmetrical distributions to data obeying a distribution of any skewness, whereby ''p'' < 1 when the skewness is positive and ''p'' > 1 when the skewness is negative. The optimal value of ''p'' is to be found by a numerical method
In numerical analysis, a numerical method is a mathematical tool designed to solve numerical problems. The implementation of a numerical method with an appropriate convergence check in a programming language is called a numerical algorithm.
Mathem ...
. The numerical method may consist of assuming a range of ''p'' values, then applying the distribution fitting procedure repeatedly for all the assumed ''p'' values, and finally selecting the value of ''p'' for which the sum of squares of deviations of calculated probabilities from measured frequencies ( chi squared) is minimum, as is done in CumFreq
In statistics and data analysis the application software CumFreq is a tool for cumulative frequency analysis of a single variable and for probability distribution fitting.
Originally the method was developed for the analysis of hydrologica ...
.
The generalization enhances the flexibility of probability distributions and increases their applicability in distribution fitting.
The versatility of generalization makes it possible, for example, to fit approximately normally distributed data sets to a large number of different probability distributions, while negatively skewed distributions can be fitted to
square normal and mirrored Gumbel distributions.Left (negatively) skewed frequency histograms can be
fitted to square normal or mirrored Gumbel probability functions/ref>
Inversion of skewness
 Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the
Skewed distributions can be inverted (or mirrored) by replacing in the mathematical expression of the cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(F) by its complement: F'=1-F, obtaining the Cumulative distribution function#Complementary cumulative distribution function (tail distribution), complementary distribution function (also called survival function) that gives a mirror image. In this manner, a distribution that is skewed to the right is transformed into a distribution that is skewed to the left and vice versa.
::
The technique of skewness inversion increases the number of probability distributions available for distribution fitting and enlarges the distribution fitting opportunities.
Shifting of distributions
Some probability distributions, like the exponential, do not support data values (''X'') equal to or less than zero. Yet, when negative data are present, such distributions can still be used replacing ''X'' by ''Y''=''X''-''Xm'', where ''Xm'' is the minimum value of ''X''. This replacement represents a shift of the probability distribution in positive direction, i.e. to the right, because ''Xm'' is negative. After completing the distribution fitting of ''Y'', the corresponding ''X''-values are found from ''X''=''Y''+''Xm'', which represents a back-shift of the distribution in negative direction, i.e. to the left.The technique of distribution shifting augments the chance to find a properly fitting probability distribution.
Composite distributions
 The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the
The option exists to use two different probability distributions, one for the lower data range, and one for the higher like for example the Laplace distribution
In probability theory and statistics, the Laplace distribution is a continuous probability distribution named after Pierre-Simon Laplace. It is also sometimes called the double exponential distribution, because it can be thought of as two exponen ...
. The ranges are separated by a break-point. The use of such composite (discontinuous) probability distributions can be opportune when the data of the phenomenon studied were obtained under two sets different conditions.
Uncertainty of prediction
 Predictions of occurrence based on fitted probability distributions are subject to uncertainty, which arises from the following conditions:
* The true probability distribution of events may deviate from the fitted distribution, as the observed data series may not be totally representative of the real probability of occurrence of the phenomenon due to random error
* The occurrence of events in another situation or in the future may deviate from the fitted distribution as this occurrence can also be subject to random error
* A change of environmental conditions may cause a change in the probability of occurrence of the phenomenon
An estimate of the uncertainty in the first and second case can be obtained with the binomial probability distribution using for example the probability of exceedance ''Pe'' (i.e. the chance that the event ''X'' is larger than a reference value ''Xr'' of ''X'') and the probability of non-exceedance ''Pn'' (i.e. the chance that the event ''X'' is smaller than or equal to the reference value ''Xr'', this is also called cumulative probability). In this case there are only two possibilities: either there is exceedance or there is non-exceedance. This duality is the reason that the binomial distribution is applicable.
With the binomial distribution one can obtain a prediction interval. Such an interval also estimates the risk of failure, i.e. the chance that the predicted event still remains outside the confidence interval. The confidence or risk analysis may include the return period ''T=1/Pe'' as is done in hydrology.
Predictions of occurrence based on fitted probability distributions are subject to uncertainty, which arises from the following conditions:
* The true probability distribution of events may deviate from the fitted distribution, as the observed data series may not be totally representative of the real probability of occurrence of the phenomenon due to random error
* The occurrence of events in another situation or in the future may deviate from the fitted distribution as this occurrence can also be subject to random error
* A change of environmental conditions may cause a change in the probability of occurrence of the phenomenon
An estimate of the uncertainty in the first and second case can be obtained with the binomial probability distribution using for example the probability of exceedance ''Pe'' (i.e. the chance that the event ''X'' is larger than a reference value ''Xr'' of ''X'') and the probability of non-exceedance ''Pn'' (i.e. the chance that the event ''X'' is smaller than or equal to the reference value ''Xr'', this is also called cumulative probability). In this case there are only two possibilities: either there is exceedance or there is non-exceedance. This duality is the reason that the binomial distribution is applicable.
With the binomial distribution one can obtain a prediction interval. Such an interval also estimates the risk of failure, i.e. the chance that the predicted event still remains outside the confidence interval. The confidence or risk analysis may include the return period ''T=1/Pe'' as is done in hydrology.

Goodness of fit
By ranking the goodness of fit of various distributions one can get an impression of which distribution is acceptable and which is not.Histogram and density function
From thecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(CDF) one can derive a histogram
A histogram is an approximate representation of the distribution of numerical data. The term was first introduced by Karl Pearson. To construct a histogram, the first step is to " bin" (or "bucket") the range of values—that is, divide the ent ...
and the probability density function (PDF).
See also
* Curve fitting * Density estimation * Mixture distribution * Product distributionReferences
{{Distribution fitting software