|
Return Period
A return period, also known as a recurrence interval or repeat interval, is an average time or an estimated average time between events such as earthquakes, floods, landslides, or river discharge flows to occur. The reciprocal value of return period is called the frequency of occurrence. It is a statistical measurement typically based on historic data over an extended period, and is used usually for risk analysis. Examples include deciding whether a project should be allowed to go forward in a zone of a certain risk or designing structures to withstand events with a certain return period. The following analysis assumes that the probability of the event occurring does not vary over time and is independent of past events. Estimating a return period Recurrence interval = :''n'' number of years on record; :''m'' is the rank of observed occurrences when arranged in descending order For floods, the event may be measured in terms of m3/s or height; for storm surges, in terms of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
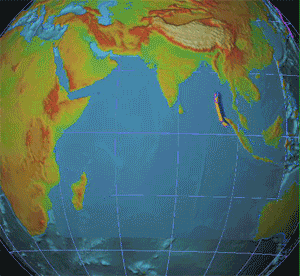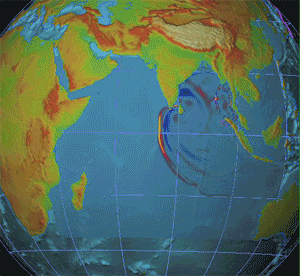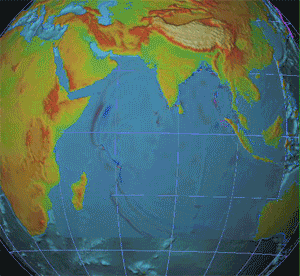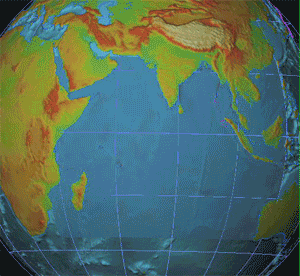
Earthquake
An earthquakealso called a quake, tremor, or tembloris the shaking of the Earth's surface resulting from a sudden release of energy in the lithosphere that creates seismic waves. Earthquakes can range in intensity, from those so weak they cannot be felt, to those violent enough to propel objects and people into the air, damage critical infrastructure, and wreak destruction across entire cities. The seismic activity of an area is the frequency, type, and size of earthquakes experienced over a particular time. The seismicity at a particular location in the Earth is the average rate of seismic energy release per unit volume. In its most general sense, the word ''earthquake'' is used to describe any seismic event that generates seismic waves. Earthquakes can occur naturally or be induced by human activities, such as mining, fracking, and nuclear weapons testing. The initial point of rupture is called the hypocenter or focus, while the ground level directly above it is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Distribution
In probability theory and statistics, the binomial distribution with parameters and is the discrete probability distribution of the number of successes in a sequence of statistical independence, independent experiment (probability theory), experiments, each asking a yes–no question, and each with its own Boolean-valued function, Boolean-valued outcome (probability), outcome: ''success'' (with probability ) or ''failure'' (with probability ). A single success/failure experiment is also called a Bernoulli trial or Bernoulli experiment, and a sequence of outcomes is called a Bernoulli process; for a single trial, i.e., , the binomial distribution is a Bernoulli distribution. The binomial distribution is the basis for the binomial test of statistical significance. The binomial distribution is frequently used to model the number of successes in a sample of size drawn with replacement from a population of size . If the sampling is carried out without replacement, the draws ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seismology
Seismology (; from Ancient Greek σεισμός (''seismós'') meaning "earthquake" and -λογία (''-logía'') meaning "study of") is the scientific study of earthquakes (or generally, quakes) and the generation and propagation of elastic waves through planetary bodies. It also includes studies of the environmental effects of earthquakes such as tsunamis; other seismic sources such as volcanoes, plate tectonics, glaciers, rivers, oceanic microseisms, and the atmosphere; and artificial processes such as explosions. Paleoseismology is a related field that uses geology to infer information regarding past earthquakes. A recording of Earth's motion as a function of time, created by a seismograph is called a seismogram. A seismologist is a scientist who works in basic or applied seismology. History Scholarly interest in earthquakes can be traced back to antiquity. Early speculations on the natural causes of earthquakes were included in the writings of Thales of Miletu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrology
Hydrology () is the scientific study of the movement, distribution, and management of water on Earth and other planets, including the water cycle, water resources, and drainage basin sustainability. A practitioner of hydrology is called a hydrologist. Hydrologists are scientists studying earth science, earth or environmental science, civil engineering, civil or environmental engineering, and physical geography. Using various analytical methods and scientific techniques, they collect and analyze data to help solve water related problems such as Environmentalism, environmental preservation, natural disasters, and Water resource management, water management. Hydrology subdivides into surface water hydrology, groundwater hydrology (hydrogeology), and marine hydrology. Domains of hydrology include hydrometeorology, surface-water hydrology, surface hydrology, hydrogeology, drainage basin, drainage-basin management, and water quality. Oceanography and meteorology are not included beca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Residence Time (statistics)
In statistics, the residence time is the average amount of time it takes for a random process to reach a certain boundary value, usually a boundary far from the mean. Definition Suppose is a real, scalar stochastic process with initial value , mean and two critical values , where and . Define the first passage time of from within the interval as : \tau(y_0) = \inf\, where "inf" is the infimum. This is the smallest time after the initial time that is equal to one of the critical values forming the boundary of the interval, assuming is within the interval. Because proceeds randomly from its initial value to the boundary, is itself a random variable. The mean of is the residence time, : \bar(y_0) = E tau(y_0)\mid y_0 For a Gaussian process and a boundary far from the mean, the residence time equals the inverse of the frequency of exceedance of the smaller critical value, : \bar = N^(\min(y_,\ y_)), where the frequency of exceedance is is the variance of the Gau ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Frequency Of Exceedance
The frequency of exceedance, sometimes called the annual rate of exceedance, is the frequency with which a random process exceeds some critical value. Typically, the critical value is far from the mean. It is usually defined in terms of the number of peaks of the random process that are outside the boundary. It has applications related to predicting extreme events, such as major earthquakes and floods. Definition The frequency of exceedance is the number of times a stochastic process exceeds some critical value, usually a critical value far from the process' mean, per unit time. Counting exceedance of the critical value can be accomplished either by counting peaks of the process that exceed the critical value or by counting upcrossings of the critical value, where an ''upcrossing'' is an event where the instantaneous value of the process crosses the critical value with positive slope. This article assumes the two methods of counting exceedance are equivalent and that the process ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
100-year Flood
A 100-year flood, also called a 1% flood,Holmes, R.R., Jr., and Dinicola, K. (2010) ''100-Year flood–it's all about chance 'U.S. Geological Survey General Information Product 106/ref> is a flood event at a level that is reached or exceeded once per hundred years, long-run probability, on average. It has a 1 in 100 chance (1% probability) of being equaled or exceeded in any given year. The estimated boundaries of inundation in a 100-year flood are marked on flood maps. Maps, elevations and flow rates For coastal flooding and lake flooding, a 100-year flood is generally expressed as a water level elevation or depth, and includes a combination of tide, storm surge, and wind wave, waves. For river systems, a 100-year flood can be expressed as a Discharge (hydrology), flow rate, from which the flood elevation is derived. The resulting area of inundation is referred to as the ''100-year floodplain''. Estimates of the 100-year flood flow rate and other streamflow statistics for any ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Mass Function
In probability and statistics, a probability mass function (sometimes called ''probability function'' or ''frequency function'') is a function that gives the probability that a discrete random variable is exactly equal to some value. Sometimes it is also known as the discrete probability density function. The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete. A probability mass function differs from a continuous probability density function (PDF) in that the latter is associated with continuous rather than discrete random variables. A continuous PDF must be integrated over an interval to yield a probability. The value of the random variable having the largest probability mass is called the mode. Formal definition Probability mass function is the probability distribution of a discrete random variable, and provides the p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Trial
In the theory of probability and statistics, a Bernoulli trial (or binomial trial) is a random experiment with exactly two possible outcomes, "success" and "failure", in which the probability of success is the same every time the experiment is conducted. It is named after Jacob Bernoulli, a 17th-century Swiss mathematician, who analyzed them in his ' (1713). The mathematical formalization and advanced formulation of the Bernoulli trial is known as the Bernoulli process. Since a Bernoulli trial has only two possible outcomes, it can be framed as a "yes or no" question. For example: *Is the top card of a shuffled deck an ace? *Was the newborn child a girl? (See human sex ratio.) Success and failure are in this context labels for the two outcomes, and should not be construed literally or as value judgments. More generally, given any probability space, for any event (set of outcomes), one can define a Bernoulli trial according to whether the event occurred or not (event or c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Flood
A flood is an overflow of water (list of non-water floods, or rarely other fluids) that submerges land that is usually dry. In the sense of "flowing water", the word may also be applied to the inflow of the tide. Floods are of significant concern in agriculture, civil engineering and public health. Environmental issues, Human changes to the environment often increase the intensity and frequency of flooding. Examples for human changes are land use changes such as deforestation and Wetland conservation, removal of wetlands, changes in waterway course or flood controls such as with levees. Global environmental issues also influence causes of floods, namely climate change which causes an Effects of climate change on the water cycle, intensification of the water cycle and sea level rise. For example, climate change makes Extreme weather, extreme weather events more frequent and stronger. This leads to more intense floods and increased flood risk. Natural types of floods include riv ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson Distribution
In probability theory and statistics, the Poisson distribution () is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time if these events occur with a known constant mean rate and independently of the time since the last event. It can also be used for the number of events in other types of intervals than time, and in dimension greater than 1 (e.g., number of events in a given area or volume). The Poisson distribution is named after French mathematician Siméon Denis Poisson. It plays an important role for discrete-stable distributions. Under a Poisson distribution with the expectation of ''λ'' events in a given interval, the probability of ''k'' events in the same interval is: :\frac . For instance, consider a call center which receives an average of ''λ ='' 3 calls per minute at all times of day. If the calls are independent, receiving one does not change the probability of when the next on ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |