Phase reversal on:
[Wikipedia]
[Google]
[Amazon]
t when the phase difference is zero, the two signals will have the same sign and will be reinforcing each other. One says that interference (wave propagation), constructive interference is occurring. At arguments t when the phases are different, the value of the sum depends on the waveform.
\varphi(t) is 180° (\pi radians), one says that the phases are ''opposite'', and that the signals are ''in antiphase''. Then the signals have opposite signs, and interference (wave propagation), destructive interference occurs.
Conversely, a ''phase reversal'' or ''phase inversion'' implies a 180-degree phase shift.
When the phase difference \varphi(t) is a quarter of turn (a right angle, or ), sinusoidal signals are sometimes said to be in ''quadrature'' (e.g., \varphi(t) increases linearly with the argument t . The periodic changes from reinforcement and opposition cause a phenomenon called
F with a shifted and possibly scaled version G of it. That is, suppose that G(t) = \alpha\,F(t + \tau) for some constants \alpha,\tau and all t . Suppose also that the origin for computing the phase of G has been shifted too. In that case, the phase difference \varphi is a constant (independent of t ), called the 'phase shift' or 'phase offset' of G relative to F . In the clock analogy, this situation corresponds to the two hands turning at the same speed, so that the angle between them is constant.
In this case, the phase shift is simply the argument shift \tau , expressed as a fraction of the common period T (in terms of the \varphi = 2\pi \left !\!\left[ \frac \right!\!\right">\frac_\right.html" ;"title="!\!\left[ \frac \right">!\!\left[ \frac \right!\!\right
If F is a "canonical" representative for a class of signals, like \sin(t) is for all sinusoidal signals, then the phase shift \varphi called simply the ''initial phase'' of G .
Therefore, when two periodic signals have the same frequency, they are always in phase, or always out of phase. Physically, this situation commonly occurs, for many reasons. For example, the two signals may be a periodic soundwave recorded by two microphones at separate locations. Or, conversely, they may be periodic soundwaves created by two separate speakers from the same electrical signal, and recorded by a single microphone. They may be a radio signal that reaches the receiving antenna in a straight line, and a copy of it that was reflected off a large building nearby.
A well-known example of phase difference is the length of shadows seen at different points of Earth. To a first approximation, if F(t) is the length seen at time t at one spot, and G is the length seen at the same time at a
F+G is either identically zero, or is a sinusoidal signal with the same period and phase, whose amplitude is the difference of the original amplitudes.
The phase shift of the co-sine function relative to the sine function is +90°. It follows that, for two sinusoidal signals F and G with same frequency and amplitudes A and B , and G has phase shift +90° relative to F , the sum F+G is a sinusoidal signal with the same frequency, with amplitude C and phase shift -90^\circ < \varphi < +90^\circ from F , such that
:C = \sqrt\quad\quad and \quad\quad\sin(\varphi) = B/C .

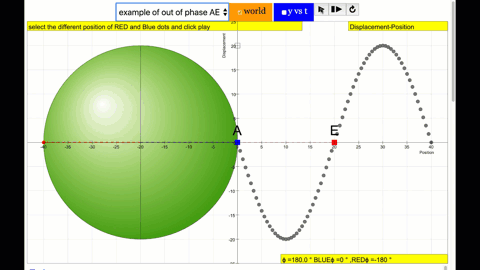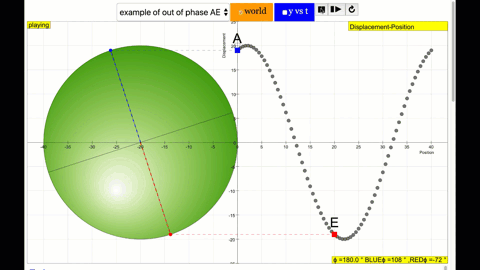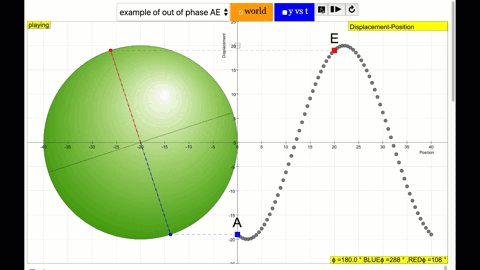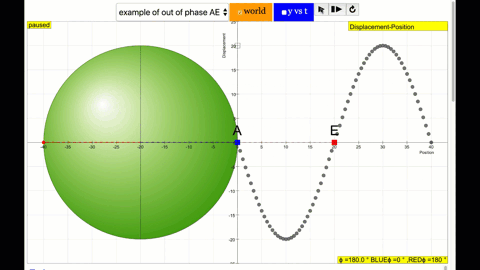 A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a
A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a
\begin
x(t) &= A\cdot \cos( 2 \pi f t + \varphi ) \\
y(t) &= A\cdot \sin( 2 \pi f t + \varphi ) = A\cdot \cos\left( 2 \pi f t + \varphi - \tfrac\right)
\end
where \textstyle A , \textstyle f , and \textstyle \varphi are constant parameters called the ''amplitude'', ''frequency'', and ''phase'' of the sinusoid. These signals are periodic with period \textstyle T = \frac , and they are identical except for a displacement of \textstyle \frac along the \textstyle t axis. The term ''phase'' can refer to several different things:
* It can refer to a specified reference, such as \textstyle \cos(2 \pi f t) , in which case we would say the ''phase'' of \textstyle x(t) is \textstyle \varphi , and the ''phase'' of \textstyle y(t) is \textstyle \varphi - \frac .
* It can refer to \textstyle \varphi , in which case we would say \textstyle x(t) and \textstyle y(t) have the same ''phase'' but are relative to their own specific references.
* In the context of communication waveforms, the time-variant angle \textstyle 2 \pi f t + \varphi , or its
What is a phase?
. Prof. Jeffrey Hass. "''An Acoustics Primer''", Section 8.
pages 1 thru 3
2013)
ECE 209: Sources of Phase Shift
— Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
Open Source Physics JavaScript HTML5
Java Applet Wave mechanics Physical quantities
In
systems, when the superposition principle holds.
For arguments physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
and mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the phase of a periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
of some real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010)
...
variable (such as time) is an angle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
-like quantity representing the fraction of the cycle covered up to . It is denoted and expressed in such a scale that it varies by one full turn as the variable goes through each period
Period may refer to:
Common uses
* Era, a length or span of time
* Full stop (or period), a punctuation mark
Arts, entertainment, and media
* Period (music), a concept in musical composition
* Periodic sentence (or rhetorical period), a concept ...
(and goes through each complete cycle). It may be measured
Measurement is the quantification of attributes of an object or event, which can be used to compare with other objects or events.
In other words, measurement is a process of determining how large or small a physical quantity is as compared t ...
in any angular unit
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles are ...
such as degrees or radians
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that c ...
, thus increasing by 360° or as the variable completes a full period.
This convention is especially appropriate for a sinusoid
A sine wave, sinusoidal wave, or just sinusoid is a mathematical curve defined in terms of the ''sine'' trigonometric function, of which it is the graph. It is a type of continuous wave and also a smooth periodic function. It occurs often in ma ...
al function, since its value at any argument then can be expressed as , the sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is oppo ...
of the phase, multiplied by some factor (the amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of amplit ...
of the sinusoid). (The cosine may be used instead of sine, depending on where one considers each period to start.)
Usually, whole turns are ignored when expressing the phase; so that is also a periodic function, with the same period as , that repeatedly scans the same range of angles as goes through each period. Then, is said to be "at the same phase" at two argument values and (that is, ) if the difference between them is a whole number of periods.
The numeric value of the phase depends on the arbitrary choice of the start of each period, and on the interval of angles that each period is to be mapped to.
The term "phase" is also used when comparing a periodic function with a shifted version of it. If the shift in is expressed as a fraction of the period, and then scaled to an angle spanning a whole turn, one gets the ''phase shift'', ''phase offset'', or ''phase difference'' of relative to . If is a "canonical" function for a class of signals, like is for all sinusoidal signals, then is called the ''initial phase'' of .
Mathematical definition
Let be a periodic signal (that is, a function of one real variable), and be its period (that is, the smallest positivereal number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real ...
such that for all ). Then the ''phase of '' ''at'' any argument is
:For sinusoids
For sinusoidal signals, when the phase differencein-phase and quadrature components
In electrical engineering, a sinusoid with angle modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are offset in phase by one-quarter cycle (90 degrees or /2 radians). All three functions have the s ...
).
If the frequencies are different, the phase difference beating
Beat, beats or beating may refer to:
Common uses
* Patrol, or beat, a group of personnel assigned to monitor a specific area
** Beat (police), the territory that a police officer patrols
** Gay beat, an area frequented by gay men
* Battery ...
.
For shifted signals
The phase difference is especially important when comparing a periodic signalmodulo operation
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the '' modulus'' of the operation).
Given two positive numbers and , modulo (often abbreviated as ) is th ...
) of the two signals and then scaled to a full turn:
:longitude
Longitude (, ) is a geographic coordinate that specifies the east–west position of a point on the surface of the Earth, or another celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter l ...
30° west of that point, then the phase difference between the two signals will be 30° (assuming that, in each signal, each period starts when the shadow is shortest).
For sinusoids with same frequency
For sinusoidal signals (and a few other waveforms, like square or symmetric triangular), a phase shift of 180° is equivalent to a phase shift of 0° with negation of the amplitude. When two signals with these waveforms, same period, and opposite phases are added together, the sum
 A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a
A real-world example of a sonic phase difference occurs in the warble of a Native American flute. The amplitude of different harmonic components of same long-held note on the flute come into dominance at different points in the phase cycle. The phase difference between the different harmonics can be observed on a spectrogram
A spectrogram is a visual representation of the spectrum of frequencies of a signal as it varies with time.
When applied to an audio signal, spectrograms are sometimes called sonographs, voiceprints, or voicegrams. When the data are represen ...
of the sound of a warbling flute.
Phase comparison
''Phase comparison'' is a comparison of the phase of two waveforms, usually of the same nominal frequency. In time and frequency, the purpose of a phase comparison is generally to determine the frequency offset (difference between signal cycles) with respect to a reference. This content has been copied and pasted from an NIST web page ''and is in the public domain''. A phase comparison can be made by connecting two signals to a two-channel oscilloscope. The oscilloscope will display two sine signals, as shown in the graphic to the right. In the adjacent image, the top sine signal is the test frequency, and the bottom sine signal represents a signal from the reference. If the two frequencies were exactly the same, their phase relationship would not change and both would appear to be stationary on the oscilloscope display. Since the two frequencies are not exactly the same, the reference appears to be stationary and the test signal moves. By measuring the rate of motion of the test signal the offset between frequencies can be determined. Vertical lines have been drawn through the points where each sine signal passes through zero. The bottom of the figure shows bars whose width represents the phase difference between the signals. In this case the phase difference is increasing, indicating that the test signal is lower in frequency than the reference.Formula for phase of an oscillation or a periodic signal
The phase of anoscillation
Oscillation is the repetitive or periodic variation, typically in time, of some measure about a central value (often a point of equilibrium) or between two or more different states. Familiar examples of oscillation include a swinging pendulum ...
or signal
In signal processing, a signal is a function that conveys information about a phenomenon. Any quantity that can vary over space or time can be used as a signal to share messages between observers. The ''IEEE Transactions on Signal Processing'' ...
refers to a sinusoidal function such as the following:
:principal value
In mathematics, specifically complex analysis, the principal values of a multivalued function are the values along one chosen branch of that function, so that it is single-valued. The simplest case arises in taking the square root of a positive ...
, is referred to as ''instantaneous phase
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''comple ...
'', often just ''phase''.
See also
*Absolute phase Absolute phase refers to the phase of a waveform relative to some standard (strictly speaking, phase is always relative). To the extent that this standard is accepted by all parties, one can speak of an absolute phase in a particular field of appli ...
* AC phase
* In-phase and quadrature components
In electrical engineering, a sinusoid with angle modulation can be decomposed into, or synthesized from, two amplitude-modulated sinusoids that are offset in phase by one-quarter cycle (90 degrees or /2 radians). All three functions have the s ...
* Instantaneous phase
Instantaneous phase and frequency are important concepts in signal processing that occur in the context of the representation and analysis of time-varying functions. The instantaneous phase (also known as local phase or simply phase) of a ''comple ...
* Lissajous curve
A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of parametric equations
: x=A\sin(at+\delta),\quad y=B\sin(bt),
which describe the superposition of two perpendicular oscillations in x and y dire ...
* Phase cancellation
In physics, interference is a phenomenon in which two waves combine by adding their displacement together at every single point in space and time, to form a resultant wave of greater, lower, or the same amplitude. Constructive and destructive ...
* Phase problem
In physics, the phase problem is the problem of loss of information concerning the phase that can occur when making a physical measurement. The name comes from the field of X-ray crystallography, where the phase problem has to be solved for the det ...
* Phase spectrum
The power spectrum S_(f) of a time series x(t) describes the distribution of power into frequency components composing that signal. According to Fourier analysis, any physical signal can be decomposed into a number of discrete frequencies, o ...
* Phase velocity
The phase velocity of a wave is the rate at which the wave propagates in any medium. This is the velocity at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave (for example, ...
* Phasor
In physics and engineering, a phasor (a portmanteau of phase vector) is a complex number representing a sinusoidal function whose amplitude (''A''), angular frequency (''ω''), and initial phase (''θ'') are time-invariant. It is related to ...
* Polarization
* Coherence
Coherence, coherency, or coherent may refer to the following:
Physics
* Coherence (physics), an ideal property of waves that enables stationary (i.e. temporally and spatially constant) interference
* Coherence (units of measurement), a deriv ...
, the quality of a wave to display a well defined phase relationship in different regions of its domain of definition
* Hilbert Transform
In mathematics and in signal processing, the Hilbert transform is a specific linear operator that takes a function, of a real variable and produces another function of a real variable . This linear operator is given by convolution with the functi ...
, A method of changing phase by 90°
* Reflection phase shift A phase change sometimes occurs when a wave is reflected, specifically from a medium with faster wave speed to the boundary of a medium with slower wave speed. Such reflections occur for many types of wave, including light waves, sound waves, and ...
, A phase change that happens when a wave is reflected off of a boundary from fast medium to slow medium
References
External links
{{Commons category, Phase (waves) *What is a phase?
. Prof. Jeffrey Hass. "''An Acoustics Primer''", Section 8.
Indiana University
Indiana University (IU) is a system of public universities in the U.S. state of Indiana.
Campuses
Indiana University has two core campuses, five regional campuses, and two regional centers under the administration of IUPUI.
*Indiana Universit ...
, 2003. See also:pages 1 thru 3
2013)
ECE 209: Sources of Phase Shift
— Discusses the time-domain sources of phase shift in simple linear time-invariant circuits.
Open Source Physics JavaScript HTML5
Java Applet Wave mechanics Physical quantities