Percolation Threshold

The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in random systems. Below the threshold a giant connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified lattice models of random systems or networks (graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability ''p'', or more generally a critical surface for a group of parameters ''p''₁, ''p''₂, ..., such that infinite connectivity (''percolation'') first occurs.

Percolation models

The most common percolation model is to take a regular lattice, like a square lattice, and make it into a random network by randomly "occupying" sites (vertices) or bonds (edges) with a statistically independent probability ''p''. At a critical threshold ''p_c'', large clusters and long-range connectivity first appears, and this is called the percolation threshold. Depending on the method for obtaining the random network, one distinguishes between the site percolation threshold and the bond percolation threshold. More general systems have several probabilities ''p''₁, ''p''₂, etc., and the transition is characterized by a ''critical surface'' or ''manifold''. One can also consider continuum systems, such as overlapping disks and spheres placed randomly, or the negative space ( ''Swiss-cheese'' models).

To understand the threshold, you can consider a quantity such as the probability that there is a continuous path from one boundary to another along occupied sites or bonds—that is, within a single cluster. For example, one can consider a square system, and ask for the probability ''P'' that there is path from the top boundary to the bottom boundary. As a function of the occupation probability ''p'', one finds a sigmoidal plot that goes from ''P=0'' at ''p=0'' to ''P=1'' at ''p=1''. The larger the square is compared to the lattice spacing, the sharper the transition will be. When the system size goes to infinity, ''P(p)'' will be a step function at the threshold value ''p_c''. For finite large systems, ''P(p_c)'' is a constant whose value depends upon the shape of the system; for the square system discussed above, ''P(p_c)='' exactly for any lattice by a simple symmetry argument.

There are other signatures of the critical threshold. For example, the size distribution (number of clusters of size ''s'') drops off as a power-law for large ''s'' at the threshold, ''n_s(p_c) ~ s^−τ'', where τ is a dimension-dependent percolation critical exponents. For an infinite system, the critical threshold corresponds to the first point (as ''p'' increases) where the size of the clusters become infinite.

In the systems described so far, it has been assumed that the occupation of a site or bond is completely random—this is the so-called ''Bernoulli percolation.'' For a continuum system, random occupancy corresponds to the points being placed by a Poisson process. Further variations involve correlated percolation, such as percolation clusters related to Ising and Potts models of ferromagnets, in which the bonds are put down by the Fortuin– Kasteleyn method.

In ''bootstrap'' or ''k-sat'' percolation, sites and/or bonds are first occupied and then successively culled from a system if a site does not have at least ''k'' neighbors. Another important model of percolation, in a different universality class altogether, is directed percolation, where connectivity along a bond depends upon the direction of the flow.

Over the last several decades, a tremendous amount of work has gone into finding exact and approximate values of the percolation thresholds for a variety of these systems. Exact thresholds are only known for certain two-dimensional lattices that can be broken up into a self-dual array, such that under a triangle-triangle transformation, the system remains the same. Studies using numerical methods have led to numerous improvements in algorithms and several theoretical discoveries.

Simple duality in two dimensions implies that all fully triangulated lattices (e.g., the triangular, union jack, cross dual, martini dual and asanoha or 3-12 dual, and the Delaunay triangulation) all have site thresholds of , and self-dual lattices (square, martini-B) have bond thresholds of .

The notation such as (4,8²) comes from Grünbaum and Shephard,

and indicates that around a given vertex, going in the clockwise direction, one encounters first a square and then two octagons. Besides the eleven Archimedean lattices composed of regular polygons with every site equivalent, many other more complicated lattices with sites of different classes have been studied.

Error bars in the last digit or digits are shown by numbers in parentheses. Thus, 0.729724(3) signifies 0.729724 ± 0.000003, and 0.74042195(80) signifies 0.74042195 ± 0.00000080. The error bars variously represent one or two standard deviations in net error (including statistical and expected systematic error), or an empirical confidence interval, depending upon the source.

Percolation on networks

For a random tree-like network without degree-degree correlation, it can be shown that such network can have a giant component, and the percolation threshold (transmission probability) is given by

$p_c = \frac = \frac$.

Where $g_1(z)$ is the generating function corresponding to the excess degree distribution, $$ is the average degree of the network and $$ is the second moment of the degree distribution. So, for example, for an ER network, since the degree distribution is a Poisson distribution, the threshold is at $p_c = ^$.

In networks with low clustering, $0 < C \ll 1$, the critical point gets scaled by $(1-C)^$ such that:

$p_c = \frac\frac.$

This indicates that for a given degree distribution, the clustering leads to a larger percolation threshold, mainly because for a fixed number of links, the clustering structure reinforces the core of the network with the price of diluting the global connections. For networks with high clustering, strong clustering could induce the core–periphery structure, in which the core and periphery might percolate at different critical points, and the above approximate treatment is not applicable.

Percolation on 2D lattices

Thresholds on Archimedean lattices

Note: sometimes "hexagonal" is used in place of honeycomb, although in some fields, a triangular lattice is also called a hexagonal lattice. ''z'' = bulk coordination number.

2d lattices with extended and complex neighborhoods

In this section, sq-1,2,3 corresponds to square (NN+2NN+3NN), etc. Equivalent to square-2N+3N+4N, sq(1,2,3). tri = triangular, hc = honeycomb.

Here NN = nearest neighbor, 2NN = second nearest neighbor (or next nearest neighbor), 3NN = third nearest neighbor (or next-next nearest neighbor), etc. These are also called 2N, 3N, 4N respectively in some papers.

*For overlapping or touching squares, $p_c$(site) given here is the net fraction of sites occupied $\phi_c$ similar to the $\phi_c$ in continuum percolation. The case of a 2×2 square is equivalent to percolation of a square lattice NN+2NN+3NN+4NN or sq-1,2,3,4 with threshold $1-(1-\phi_c)^ = 0.196724(10)\ldots$ with $\phi_c= 0.58365(2)$. The 3×3 square corresponds to sq-1,2,3,4,5,6,7,8 with ''z''=44 and $p_c=1-(1-\phi_c)^ = 0.095765(5)\ldots$. The value of ''z'' for a ''k'' x ''k'' square is (2''k''+1)²-5. For larger overlapping squares, see.

Overlapping shapes on 2D lattices

Site threshold is number of overlapping objects per lattice site. ''k'' is the length (net area). Overlapping squares are shown in the complex neighborhood section. Here z is the coordination number to k-mers of either orientation, with $z = k^2+10k-2$.

The coverage is calculated from $p_c$ by $\phi_c = 1-(1-p_c)^$

Approximate formulas for thresholds of Archimedean lattices

Site-bond percolation in 2D

Site bond percolation. Here $p_s$ is the site occupation probability and $p_b$ is the bond occupation probability, and connectivity is made only if both the sites and bonds along a path are occupied. The criticality condition becomes a curve $f(p_,p_)$ = 0, and some specific critical pairs $(p_,p_)$ are listed below.

Square lattice:

Honeycomb (hexagonal) lattice:

Kagome lattice:

* For values on different lattices, see "An investigation of site-bond percolation on many lattices".

Approximate formula for site-bond percolation on a honeycomb lattice

Archimedean duals (Laves lattices)

Laves lattices are the duals to the Archimedean lattices. Drawings from. See also Uniform tilings.

2-uniform lattices

Top 3 lattices: #13 #12 #36


Bottom 3 lattices: #34 #37 #11

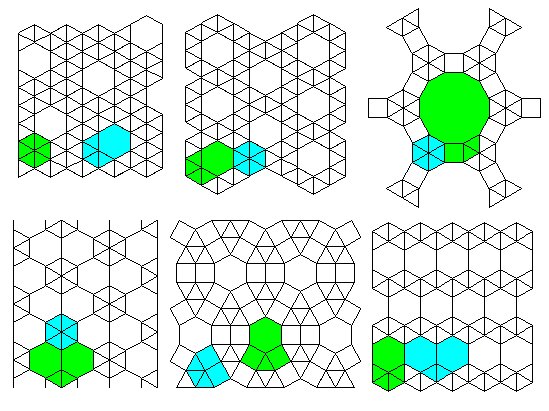
Top 2 lattices: #35 #30


Bottom 2 lattices: #41 #42

Top 4 lattices: #22 #23 #21 #20


Bottom 3 lattices: #16 #17 #15

Top 2 lattices: #31 #32


Bottom lattice: #33

Inhomogeneous 2-uniform lattice

This figure shows something similar to the 2-uniform lattice #37, except the polygons are not all regular—there is a rectangle in the place of the two squares—and the size of the polygons is changed. This lattice is in the isoradial representation in which each polygon is inscribed in a circle of unit radius. The two squares in the 2-uniform lattice must now be represented as a single rectangle in order to satisfy the isoradial condition. The lattice is shown by black edges, and the dual lattice by red dashed lines. The green circles show the isoradial constraint on both the original and dual lattices. The yellow polygons highlight the three types of polygons on the lattice, and the pink polygons highlight the two types of polygons on the dual lattice. The lattice has vertex types ()(3³,4²) + ()(3,4,6,4), while the dual lattice has vertex types ()(4⁶)+()(4²,5²)+()(5³)+()(5²,4). The critical point is where the longer bonds (on both the lattice and dual lattice) have occupation probability p = 2 sin (Ï€/18) = 0.347296... which is the bond percolation threshold on a triangular lattice, and the shorter bonds have occupation probability 1 − 2 sin(Ï€/18) = 0.652703..., which is the bond percolation on a hexagonal lattice. These results follow from the isoradial condition but also follow from applying the star-triangle transformation to certain stars on the honeycomb lattice. Finally, it can be generalized to having three different probabilities in the three different directions, p₁, p₂ and ''p''₃ for the long bonds, and , , and for the short bonds, where ''p''₁, ''p''₂ and ''p''₃ satisfy the critical surface for the inhomogeneous triangular lattice.

Thresholds on 2D bow-tie and martini lattices

To the left, center, and right are: the martini lattice, the martini-A lattice, the martini-B lattice. Below: the martini covering/medial lattice, same as the 2×2, 1×1 subnet for kagome-type lattices (removed).

Some other examples of generalized bow-tie lattices (a-d) and the duals of the lattices (e-h):

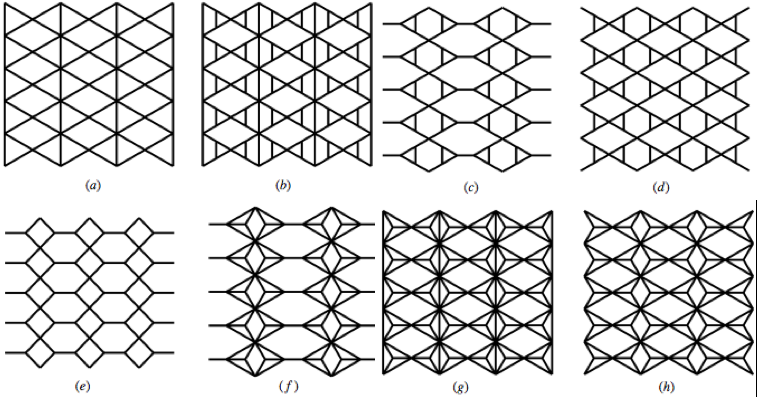
Thresholds on 2D covering, medial, and matching lattices

Thresholds on 2D chimera non-planar lattices

Thresholds on subnet lattices

The 2 x 2, 3 x 3, and 4 x 4 subnet kagome lattices. The 2 × 2 subnet is also known as the "triangular kagome" lattice.

Thresholds of random sequentially adsorbed objects

(For more results and comparison to the jamming density, see Random sequential adsorption)

The threshold gives the fraction of sites occupied by the objects when site percolation first takes place (not at full jamming). For longer k-mers see Ref.

Thresholds of full dimer coverings of two dimensional lattices

Here, we are dealing with networks that are obtained by covering a lattice with dimers, and then consider bond percolation on the remaining bonds. In discrete mathematics, this problem is known as the 'perfect matching' or the 'dimer covering' problem.

Thresholds of polymers (random walks) on a square lattice

System is composed of ordinary (non-avoiding) random walks of length l on the square lattice.

Thresholds of self-avoiding walks of length k added by random sequential adsorption

Thresholds on 2D inhomogeneous lattices

Thresholds for 2D continuum models

$\eta_c = \pi r^2 N / L^2$ equals critical total area for disks, where N is the number of objects and L is the system size.

$4 \eta_c$ gives the number of disk centers within the circle of influence (radius 2 r).

$r_c = L \sqrt$ is the critical disk radius.

$\eta_c = \pi a b N / L^2$ for ellipses of semi-major and semi-minor axes of a and b, respectively. Aspect ratio $\epsilon = a / b$ with $a > b$.

$\eta_c = \ell m N / L^2$ for rectangles of dimensions $\ell$ and $m$. Aspect ratio $\epsilon = \ell/m$ with $\ell > m$.

$\eta_c = \pi x N / (4 L^2 (x-2))$ for power-law distributed disks with $\hbox\ge R) = R^$, $R \ge 1$.

$\phi_c = 1 - e^$ equals critical area fraction.

$n_c = \ell^2 N / L^2$ equals number of objects of maximum length $\ell = 2 a$ per unit area.

For ellipses, $n_c = (4 \epsilon / \pi)\eta_c$

For void percolation, $\phi_c = e^$ is the critical void fraction.

For more ellipse values, see

For more rectangle values, see

Both ellipses and rectangles belong to the superellipses, with $, x/a, ^+, y/b, ^=1$. For more percolation values of superellipses, see.

For the monodisperse particle systems, the percolation thresholds of concave-shaped superdisks are obtained as seen in

For binary dispersions of disks, see

Thresholds on 2D random and quasi-lattices

*Theoretical estimate

Thresholds on 2D correlated systems

Assuming power-law correlations $C(r) \sim , r, ^$

Thresholds on slabs

''h'' is the thickness of the slab, ''h'' × ∞ × ∞. Boundary conditions (b.c.) refer to the top and bottom planes of the slab.

Thresholds on 3D lattices and 3D continuum space

Filling factor = fraction of space filled by touching spheres at every lattice site (for systems with uniform bond length only). Also called Atomic Packing Factor.

Filling fraction (or Critical Filling Fraction) = filling factor * p_c(site).

NN = nearest neighbor, 2NN = next-nearest neighbor, 3NN = next-next-nearest neighbor, etc.

kxkxk cubes are cubes of occupied sites on a lattice, and are equivalent to extended-range percolation of a cube of length (2k+1), with edges and corners removed, with z = (2k+1)³-12(2k-1)-9 (center site not counted in z).

Question: the bond thresholds for the hcp and fcc lattice
agree within the small statistical error. Are they identical,
and if not, how far apart are they? Which threshold is expected to be bigger? Similarly for the ice and diamond lattices. See

Overlapping shapes on 3D lattices

Site threshold is the number of overlapping objects per lattice site. The coverage φ_c is the net fraction of sites covered, and ''v'' is the volume (number of cubes). Overlapping cubes are given in the section on thresholds of 3D lattices. Here z is the coordination number to k-mers of either orientation, with $z=6k^2+18k-4$

The coverage is calculated from $p_c$ by $\phi_c = 1-(1-p_c)^$ for sticks, and $\phi_c = 1-(1-p_c)^$ for plaquettes.

Dimer percolation in 3D

Thresholds for 3D continuum models

All overlapping except for jammed spheres and polymer matrix.

$\eta_c = (4/3) \pi r^3 N / L^3$ is the total volume (for spheres), where N is the number of objects and L is the system size.

$\phi_c = 1 - e^$ is the critical volume fraction, valid for overlapping randomly placed objects.

For disks and plates, these are effective volumes and volume fractions.

For void ("Swiss-Cheese" model), $\phi_c = e^$ is the critical void fraction.

For more results on void percolation around ellipsoids and elliptical plates, see.

For more ellipsoid percolation values see.

For spherocylinders, H/D is the ratio of the height to the diameter of the cylinder, which is then capped by hemispheres. Additional values are given in.

For superballs, m is the deformation parameter, the percolation values are given in., In addition, the thresholds of concave-shaped superballs are also determined in

For cuboid-like particles (superellipsoids), m is the deformation parameter, more percolation values are given in.

Void percolation in 3D

Void percolation refers to percolation in the space around overlapping objects. Here $\phi_c$ refers to the fraction of the space occupied by the voids (not of the particles) at the critical point, and is related to $\eta_c$ by
$\phi_c = e^$. $\eta_c$ is defined as in the continuum percolation section above.

Thresholds on 3D random and quasi-lattices

Thresholds for other 3D models

$^*$ In drilling percolation, the site threshold $p_c$ represents the fraction of columns in each direction that have not been removed, and $\phi_c=p_c^3$. For the 1d drilling, we have $\phi_c = p_c$(columns) $p_c$(sites).

^† In tube percolation, the bond threshold represents the value of the parameter $\mu$ such that the probability of putting a bond between neighboring vertical tube segments is $1-e^$, where $h_i$ is the overlap height of two adjacent tube segments.

Thresholds in different dimensional spaces

Continuum models in higher dimensions

\eta_c = (\pi^/ \Gamma /2 + 1 r^d N / L^d.

In 4d, $\eta_c = (1/2) \pi^2 r^4 N / L^4$.

In 5d, $\eta_c = (8/15) \pi^2 r^5 N / L^5$.

In 6d, $\eta_c = (1/6) \pi^3 r^6 N / L^6$.

$\phi_c = 1 - e^$ is the critical volume fraction, valid for overlapping objects.

For void models, $\phi_c = e^$ is the critical void fraction, and $\eta_c$ is the total volume of the overlapping objects

Thresholds on hypercubic lattices

For thresholds on high dimensional hypercubic lattices, we have the asymptotic series expansions

$p_c^\mathrm(d)=\sigma^+\frac\sigma^+\frac\sigma^+\frac\sigma^+\frac\sigma^+\frac\sigma^+(\sigma^)$

$p_c^\mathrm(d)=\sigma^+\frac\sigma^+\frac\sigma^+57\sigma^+\frac\sigma^+(\sigma^)$

where $\sigma = 2 d - 1$.

Thresholds in other higher-dimensional lattices

Thresholds in one-dimensional long-range percolation

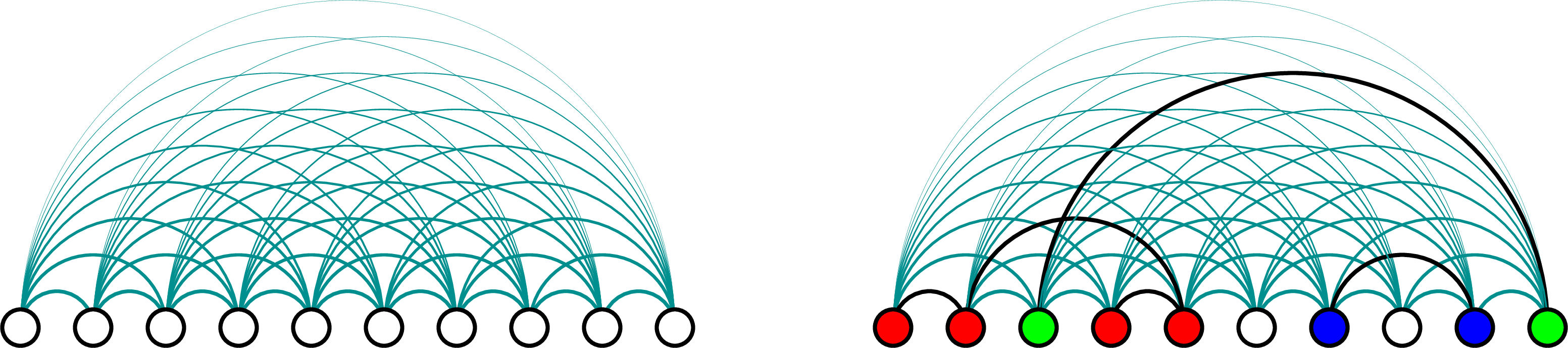In a one-dimensional chain we establish bonds between distinct sites $i$ and $j$ with probability $p=\frac$ decaying as a power-law with an exponent $\sigma>0$. Percolation occurs at a critical value $C_c<1$ for $\sigma<1$. The numerically determined percolation thresholds are given by:

Thresholds on hyperbolic, hierarchical, and tree lattices

In these lattices there may be two percolation thresholds: the lower threshold is the probability above which infinite clusters appear, and the upper is the probability above which there is a unique infinite cluster.

Note: is the Schläfli symbol, signifying a hyperbolic lattice in which n regular m-gons meet at every vertex

For bond percolation on , we have by duality $p_(P,Q) + p_(Q,P) = 1$. For site percolation, $p_(3,Q) + p_(3,Q) = 1$ because of the self-matching of triangulated lattices.

Cayley tree (Bethe lattice) with coordination number $z : p_c = 1 / ( z - 1 )$

Thresholds for directed percolation

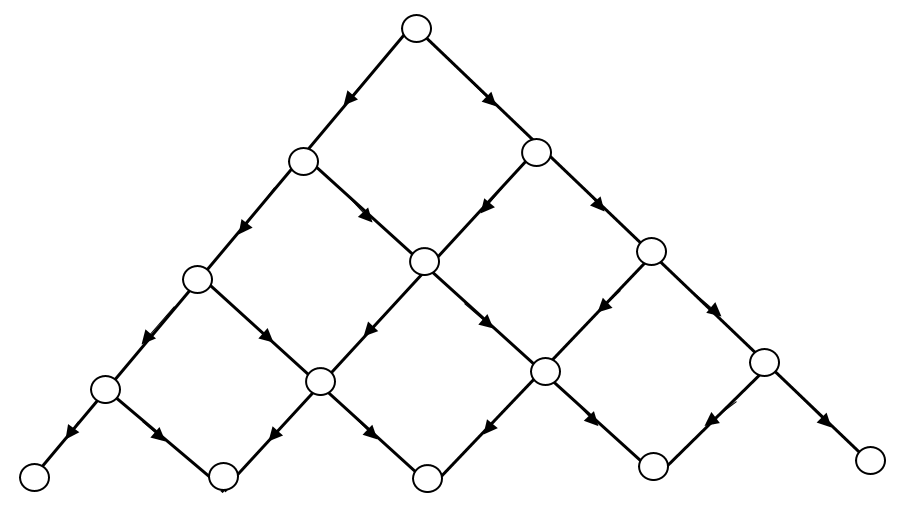
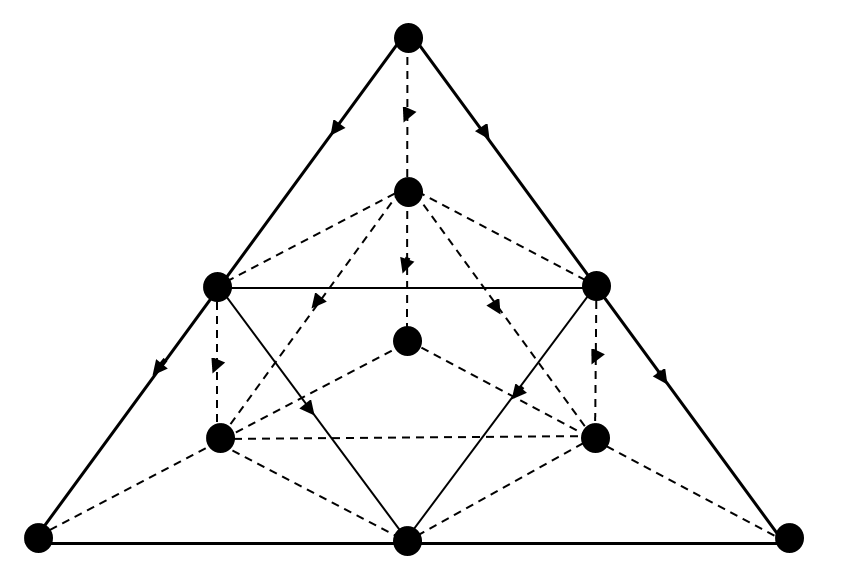
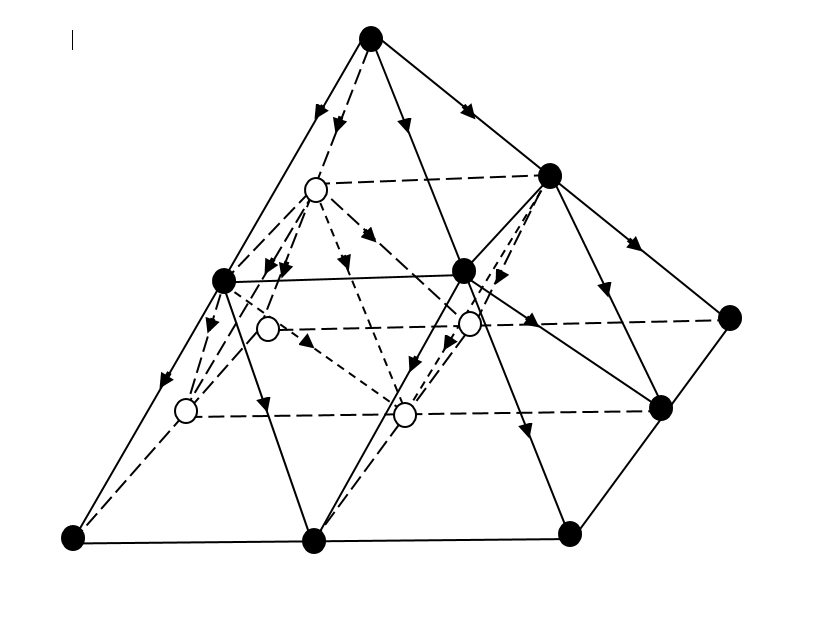nn = nearest neighbors. For a (''d'' + 1)-dimensional hypercubic system, the hypercube is in d dimensions and the time direction points to the 2D nearest neighbors.

Exact critical manifolds of inhomogeneous systems

Inhomogeneous triangular lattice bond percolation

$1 - p_1 - p_2 - p_3 + p_1 p_2 p_3 = 0$

Inhomogeneous honeycomb lattice bond percolation = kagome lattice site percolation

$1 - p_1 p_2 - p_1 p_3 - p_2 p_3+ p_1 p_2 p_3 = 0$

Inhomogeneous (3,12^2) lattice, site percolation

$1 - 3(s_1s_2)^2 + (s_1s_2)^3 = 0,$
or $s_1 s_2 = 1 - 2 \sin(\pi/18)$

Inhomogeneous union-jack lattice, site percolation with probabilities $p_1, p_2, p_3, p_4$

$p_3 = 1 - p_1; \qquad p_4 = 1 - p_2$

Inhomogeneous martini lattice, bond percolation

$1 - (p_1 p_2 r_3 + p_2 p_3 r_1 + p_1 p_3 r_2) - (p_1 p_2 r_1 r_2 + p_1 p_3 r_1 r_3 + p_2 p_3 r_2 r_3) + p_1 p_2 p_3 ( r_1 r_2 + r_1 r_3 + r_2 r_3) + r_1 r_2 r_3 (p_1 p_2 + p_1 p_3 + p_2 p_3) - 2 p_1 p_2 p_3 r_1 r_2 r_3 = 0$

Inhomogeneous martini lattice, site percolation. ''r'' = site in the star

$1 - r (p_1 p_2 + p_1 p_3 + p_2 p_3 - p_1 p_2 p_3) = 0$

Inhomogeneous martini-A (3–7) lattice, bond percolation. Left side (top of "A" to bottom): $r_2,\ p_1$. Right side: $r_1, \ p_2$. Cross bond: $\ r_3$.

$1 - p_1 r_2 - p_2 r_1 - p_1 p_2 r_3 - p_1 r_1 r_3 - p_2 r_2 r_3 + p_1 p_2 r_1 r_3 + p_1 p_2 r_2 r_3 + p_1 r_1 r_2 r_3+ p_2 r_1 r_2 r_3 - p_1 p_2 r_1 r_2 r_3 = 0$

Inhomogeneous martini-B (3–5) lattice, bond percolation

Inhomogeneous martini lattice with outside enclosing triangle of bonds, probabilities $y, x, z$ from inside to outside, bond percolation

1 - 3 z + z^3-(1-z^2) x^2 y (1 + y - y^2)(1 + z) + x^3 y^2 (3 - 2 y)(1 + 2 z) = 0

Inhomogeneous checkerboard lattice, bond percolation

$1 - (p_1 p_2 + p_1 p_3 + p_1 p_4 + p_2 p_3 + p_2 p_4 + p_3 p_4) + p_1 p_2 p_3 + p_1 p_2 p_4 + p_1 p_3 p_4 + p_2 p_3 p_4 = 0$

Inhomogeneous bow-tie lattice, bond percolation

$1 - (p_1 p_2 + p_1 p_3 + p_1 p_4 + p_2 p_3 + p_2 p_4 + p_3 p_4) + p_1 p_2 p_3 + p_1 p_2 p_4 + p_1 p_3 p_4 + p_2 p_3 p_4 - u(1 - p_1 p_2 - p_3 p_4 + p_1 p_2 p_3 p_4) = 0$

where $p_1, p_2, p_3, p_4$ are the four bonds around the square and $u$ is the diagonal bond connecting the vertex between bonds $p_4, p_1$ and $p_2, p_3$.

See also

* 2D percolation cluster
* Bootstrap percolation
* Directed percolation
* Effective medium approximations
* Epidemic models on lattices
* Graph theory
* Network science
* Percolation
* Percolation critical exponents
* Percolation theory
* Random sequential adsorption
* Uniform tilings

References

{{DEFAULTSORT:Percolation Threshold
Percolation theory
Critical phenomena
Random graphs