|
Clustering Coefficient
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterised by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998). Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes. Local clustering coefficient The local clustering coefficient of a vertex (node) in a graph quantifies how close its neighbours are to being a clique (complete graph). Duncan J. Watts and Steven Strogatz introduced the measure in 1998 to determine whether a graph is a small-world network ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
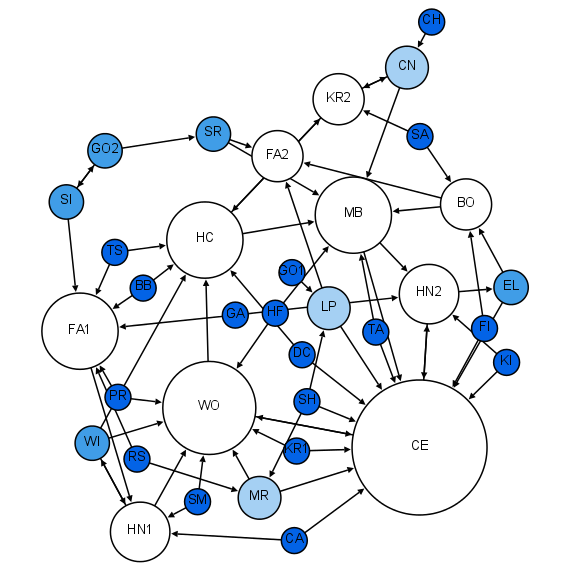
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bipartite Graph
In the mathematical field of graph theory, a bipartite graph (or bigraph) is a graph whose vertices can be divided into two disjoint and independent sets U and V, that is every edge connects a vertex in U to one in V. Vertex sets U and V are usually called the ''parts'' of the graph. Equivalently, a bipartite graph is a graph that does not contain any odd-length cycles. The two sets U and V may be thought of as a coloring of the graph with two colors: if one colors all nodes in U blue, and all nodes in V red, each edge has endpoints of differing colors, as is required in the graph coloring problem.. In contrast, such a coloring is impossible in the case of a non-bipartite graph, such as a triangle: after one node is colored blue and another red, the third vertex of the triangle is connected to vertices of both colors, preventing it from being assigned either color. One often writes G=(U,V,E) to denote a bipartite graph whose partition has the parts U and V, with E denoting ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Invariants
Graph may refer to: Mathematics *Graph (discrete mathematics), a structure made of vertices and edges **Graph theory, the study of such graphs and their properties *Graph (topology), a topological space resembling a graph in the sense of discrete mathematics *Graph of a function *Graph of a relation *Graph paper *Chart, a means of representing data (also called a graph) Computing *Graph (abstract data type), an abstract data type representing relations or connections *graph (Unix), Unix command-line utility *Conceptual graph, a model for knowledge representation and reasoning Other uses * HMS ''Graph'', a submarine of the UK Royal Navy See also *Complex network *Graf *Graff (other) *Graph database *Grapheme, in linguistics *Graphemics *Graphic (other) *-graphy (suffix from the Greek for "describe," "write" or "draw") *List of information graphics software *Statistical graphics Statistical graphics, also known as statistical graphical techniques, are graphic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Small-world Network
A small-world network is a type of mathematical graph in which most nodes are not neighbors of one another, but the neighbors of any given node are likely to be neighbors of each other and most nodes can be reached from every other node by a small number of hops or steps. Specifically, a small-world network is defined to be a network where the typical distance ''L'' between two randomly chosen nodes (the number of steps required) grows proportionally to the logarithm of the number of nodes ''N'' in the network, that is: :L \propto \log N while the global clustering coefficient is not small. In the context of a social network, this results in the small world phenomenon of strangers being linked by a short chain of acquaintances. Many empirical graphs show the small-world effect, including social networks, wikis such as Wikipedia, gene networks, and even the underlying architecture of the Internet. It is the inspiration for many network-on-chip architectures in contempo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Scale Free Network
A scale-free network is a network whose degree distribution follows a power law, at least asymptotically. That is, the fraction ''P''(''k'') of nodes in the network having ''k'' connections to other nodes goes for large values of ''k'' as : P(k) \ \sim \ k^\boldsymbol where \gamma is a parameter whose value is typically in the range 2<\gamma<3 (wherein the second moment ( scale parameter) of is infinite but the first moment is finite), although occasionally it may lie outside these bounds. Many networks have been reported to be scale-free, although statistical analysis has refuted many of these claims and seriously questioned others. Additionally, some have argued that simply knowing that a degree-distribution is [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percolation Theory
In statistical physics and mathematics, percolation theory describes the behavior of a network when nodes or links are added. This is a geometric type of phase transition, since at a critical fraction of addition the network of small, disconnected clusters merge into significantly larger connected, so-called spanning clusters. The applications of percolation theory to materials science and in many other disciplines are discussed here and in the articles network theory and percolation. Introduction A representative question (and the source of the name) is as follows. Assume that some liquid is poured on top of some porous material. Will the liquid be able to make its way from hole to hole and reach the bottom? This physical question is modelled mathematically as a three-dimensional network of vertices, usually called "sites", in which the edge or "bonds" between each two neighbors may be open (allowing the liquid through) with probability , or closed with probability , and th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Science
Network science is an academic field which studies complex networks such as telecommunication networks, computer networks, biological networks, cognitive and semantic networks, and social networks, considering distinct elements or actors represented by ''nodes'' (or ''vertices'') and the connections between the elements or actors as ''links'' (or ''edges''). The field draws on theories and methods including graph theory from mathematics, statistical mechanics from physics, data mining and information visualization from computer science, inferential modeling from statistics, and social structure from sociology. The United States National Research Council defines network science as "the study of network representations of physical, biological, and social phenomena leading to predictive models of these phenomena." Background and history The study of networks has emerged in diverse disciplines as a means of analyzing complex relational data. The earliest known paper in this f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Network Theory
Network theory is the study of graphs as a representation of either symmetric relations or asymmetric relations between discrete objects. In computer science and network science, network theory is a part of graph theory: a network can be defined as a graph in which nodes and/or edges have attributes (e.g. names). Network theory has applications in many disciplines including statistical physics, particle physics, computer science, electrical engineering, biology, archaeology, economics, finance, operations research, climatology, ecology, public health, sociology, and neuroscience. Applications of network theory include logistical networks, the World Wide Web, Internet, gene regulatory networks, metabolic networks, social networks, epistemological networks, etc.; see List of network theory topics for more examples. Euler's solution of the Seven Bridges of Königsberg problem is considered to be the first true proof in the theory of networks. Network optimization Network pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics, graph theory is the study of ''graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are connected by '' edges'' (also called ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a set of vertices (also called nodes or points); * E \subseteq \, a set of edges (also called links or lines), which are unordered pairs of vertices (that is, an edge is associated with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Degree Distribution
In the study of graphs and networks, the degree of a node in a network is the number of connections it has to other nodes and the degree distribution is the probability distribution of these degrees over the whole network. Definition The degree of a node in a network (sometimes referred to incorrectly as the connectivity) is the number of connections or edges the node has to other nodes. If a network is directed, meaning that edges point in one direction from one node to another node, then nodes have two different degrees, the in-degree, which is the number of incoming edges, and the out-degree, which is the number of outgoing edges. The degree distribution ''P''(''k'') of a network is then defined to be the fraction of nodes in the network with degree ''k''. Thus if there are ''n'' nodes in total in a network and ''n''''k'' of them have degree ''k'', we have P(k) = \frac. The same information is also sometimes presented in the form of a ''cumulative degree distribution'', the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Percolation Threshold
The percolation threshold is a mathematical concept in percolation theory that describes the formation of long-range connectivity in Randomness, random systems. Below the threshold a giant connected component (graph theory), connected component does not exist; while above it, there exists a giant component of the order of system size. In engineering and coffee making, percolation represents the flow of fluids through porous media, but in the mathematics and physics worlds it generally refers to simplified Lattice model (physics), lattice models of random systems or networks (Graph (discrete mathematics), graphs), and the nature of the connectivity in them. The percolation threshold is the critical value of the occupation probability ''p'', or more generally a critical surface for a group of parameters ''p''1, ''p''2, ..., such that infinite connectivity (''percolation'') first occurs. Percolation models The most common percolation model is to take a regular lattice, like a squar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |