Percentile on:
[Wikipedia]
[Google]
[Amazon]
In
 The methods given in the ''definitions section'' (below) are approximations for use in small-sample statistics. In general terms, for very large populations following a
The methods given in the ''definitions section'' (below) are approximations for use in small-sample statistics. In general terms, for very large populations following a
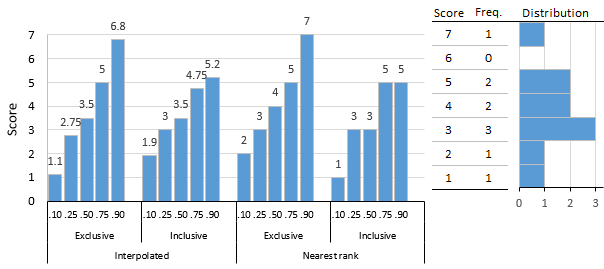 There are many formulas or algorithms for a percentile score. Hyndman and Fan identified nine and most statistical and spreadsheet software use one of the methods they describe. Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
There are many formulas or algorithms for a percentile score. Hyndman and Fan identified nine and most statistical and spreadsheet software use one of the methods they describe. Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
 One definition of percentile, often given in texts, is that the ''P''-th percentile of a list of ''N'' ordered values (sorted from least to greatest) is the smallest value in the list such that no more than ''P'' percent of the data is strictly less than the value and at least ''P'' percent of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The ordinal
One definition of percentile, often given in texts, is that the ''P''-th percentile of a list of ''N'' ordered values (sorted from least to greatest) is the smallest value in the list such that no more than ''P'' percent of the data is strictly less than the value and at least ''P'' percent of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The ordinal
statistics
Statistics (from German language, German: ''wikt:Statistik#German, Statistik'', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of ...
, a ''k''-th percentile (percentile score or centile) is a score ''below which'' a given percentage
In mathematics, a percentage (from la, per centum, "by a hundred") is a number or ratio expressed as a fraction of 100. It is often denoted using the percent sign, "%", although the abbreviations "pct.", "pct" and sometimes "pc" are also us ...
''k'' of scores in its frequency distribution
In statistics, the frequency (or absolute frequency) of an event i is the number n_i of times the observation has occurred/recorded in an experiment or study. These frequencies are often depicted graphically or in tabular form.
Types
The cumula ...
falls (exclusive definition) or a score ''at or below which'' a given percentage falls (inclusive definition).
For example, the 50th percentile (the median) is the score below which 50% of the scores in the distribution are found (by the "exclusive" definition), or at or below which 50% of the scores are found (by the "inclusive" definition).
Percentiles are expressed in the same unit of measurement
A unit of measurement is a definite magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other quantity of that kind can be expressed as a multi ...
as the input scores; for example, if the scores refer to human weight
Human body weight is a person's mass or weight.
Strictly speaking, body weight is the measurement of weight without items located on the person. Practically though, body weight may be measured with clothes on, but without shoes or heavy accessor ...
, the corresponding percentiles will be expressed in kilograms or pounds.
The percentile score and the '' percentile rank'' are related terms. The percentile rank of a score is the percentage of scores in its distribution that are less than it, an exclusive definition, and one that can be expressed with a single, simple formula.
Percentile scores and percentile ranks are often used in the reporting of test score
A test score is a piece of information, usually a number, that conveys the performance of an examinee on a test. One formal definition is that it is "a summary of the evidence contained in an examinee's responses to the items of a test that are r ...
s from norm-referenced tests, but, as just noted, they are not the same. For percentile rank, a score is given and a percentage is computed. Percentile ranks are exclusive. If the percentile rank for a specified score is 90%, then 90% of the scores were lower. In contrast, for percentiles a percentage is given and a corresponding score is determined, which can be either exclusive or inclusive. The score for a specified percentage (e.g., 90th) indicates a score below which (exclusive definition) or at or below which (inclusive definition) other scores in the distribution fall.
The 25th percentile is also known as the first '' quartile'' (''Q''1), the 50th percentile as the median or second quartile (''Q''2), and the 75th percentile as the third quartile (''Q''3).
Applications
WhenISPs
An Internet service provider (ISP) is an organization that provides services for accessing, using, or participating in the Internet. ISPs can be organized in various forms, such as commercial, community-owned, non-profit, or otherwise private ...
bill "burstable" internet bandwidth, the 95th or 98th percentile usually cuts off the top 5% or 2% of bandwidth peaks in each month, and then bills at the nearest rate. In this way, infrequent peaks are ignored, and the customer is charged in a fairer way. The reason this statistic is so useful in measuring data throughput is that it gives a very accurate picture of the cost of the bandwidth. The 95th percentile says that 95% of the time, the usage is below this amount: so, the remaining 5% of the time, the usage is above that amount.
Physicians will often use infant and children's weight and height to assess their growth in comparison to national averages and percentiles which are found in growth chart
A growth chart is used by pediatricians and other health care providers to follow a child's growth over time. Growth charts have been constructed by observing the growth of large numbers of healthy children over time. The height, weight, and hea ...
s.
The 85th percentile speed of traffic on a road is often used as a guideline in setting speed limit
Speed limits on road traffic, as used in most countries, set the legal maximum speed at which vehicles may travel on a given stretch of road. Speed limits are generally indicated on a traffic sign reflecting the maximum permitted speed - expre ...
s and assessing whether such a limit is too high or low.
In finance, value at risk
Value at risk (VaR) is a measure of the risk of loss for investments. It estimates how much a set of investments might lose (with a given probability), given normal market conditions, in a set time period such as a day. VaR is typically used by ...
is a standard measure to assess (in a model-dependent way) the quantity under which the value of the portfolio is not expected to sink within a given period of time and given a confidence value.
The normal distribution and percentiles
normal distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
:
f(x) = \frac e^
The parameter \mu ...
, percentiles may often be represented by reference to a normal curve plot. The normal distribution is plotted along an axis scaled to standard deviation
In statistics, the standard deviation is a measure of the amount of variation or dispersion of a set of values. A low standard deviation indicates that the values tend to be close to the mean (also called the expected value) of the set, while ...
s, or sigma () units. Mathematically, the normal distribution extends to negative infinity
Infinity is that which is boundless, endless, or larger than any natural number. It is often denoted by the infinity symbol .
Since the time of the ancient Greeks, the philosophical nature of infinity was the subject of many discussions amo ...
on the left and positive infinity on the right. Note, however, that only a very small proportion of individuals in a population will fall outside the −3''σ'' to +3''σ'' range. For example, with human heights very few people are above the +3''σ'' height level.
Percentiles represent the area under the normal curve, increasing from left to right. Each standard deviation represents a fixed percentile. Thus, rounding to two decimal places, −3''σ'' is the 0.13th percentile, −2''σ'' the 2.28th percentile, −1''σ'' the 15.87th percentile, 0''σ'' the 50th percentile (both the mean and median of the distribution), +1''σ'' the 84.13th percentile, +2''σ'' the 97.72nd percentile, and +3''σ'' the 99.87th percentile. This is related to the 68–95–99.7 rule or the three-sigma rule. Note that in theory the 0th percentile falls at negative infinity and the 100th percentile at positive infinity, although in many practical applications, such as test results, natural lower and/or upper limits are enforced.
Definitions
There is no standard definition of percentile, however all definitions yield similar results when the number of observations is very large and the probability distribution is continuous. In the limit, as the sample size approaches infinity, the 100''p''th percentile (0<''p''<1) approximates the inverse of thecumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ev ...
(CDF) thus formed, evaluated at ''p'', as ''p'' approximates the CDF. This can be seen as a consequence of the Glivenko–Cantelli theorem
In the theory of probability, the Glivenko–Cantelli theorem (sometimes referred to as the Fundamental Theorem of Statistics), named after Valery Ivanovich Glivenko and Francesco Paolo Cantelli, determines the asymptotic behaviour of the empir ...
. Some methods for calculating the percentiles are given below.
Calculation methods
 There are many formulas or algorithms for a percentile score. Hyndman and Fan identified nine and most statistical and spreadsheet software use one of the methods they describe. Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
There are many formulas or algorithms for a percentile score. Hyndman and Fan identified nine and most statistical and spreadsheet software use one of the methods they describe. Algorithms either return the value of a score that exists in the set of scores (nearest-rank methods) or interpolate between existing scores and are either exclusive or inclusive.
The figure shows a 10-score distribution, illustrates the percentile scores that result from these different algorithms, and serves as an introduction to the examples given subsequently. The simplest are nearest-rank methods that return a score from the distribution, although compared to interpolation methods, results can be a bit crude. The Nearest-Rank Methods table shows the computational steps for exclusive and inclusive methods.
Interpolation methods, as the name implies, can return a score that is between scores in the distribution. Algorithms used by statistical programs typically use interpolation methods, for example, the percentile.exc and percentile.inc functions in Microsoft Excel. The Interpolated Methods table shows the computational steps.
The nearest-rank method
 One definition of percentile, often given in texts, is that the ''P''-th percentile of a list of ''N'' ordered values (sorted from least to greatest) is the smallest value in the list such that no more than ''P'' percent of the data is strictly less than the value and at least ''P'' percent of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The ordinal
One definition of percentile, often given in texts, is that the ''P''-th percentile of a list of ''N'' ordered values (sorted from least to greatest) is the smallest value in the list such that no more than ''P'' percent of the data is strictly less than the value and at least ''P'' percent of the data is less than or equal to that value. This is obtained by first calculating the ordinal rank and then taking the value from the ordered list that corresponds to that rank. The ordinal rank
Rank is the relative position, value, worth, complexity, power, importance, authority, level, etc. of a person or object within a ranking, such as:
Level or position in a hierarchical organization
* Academic rank
* Diplomatic rank
* Hierarchy
* H ...
''n'' is calculated using this formula
:
* Using the nearest-rank method on lists with fewer than 100 distinct values can result in the same value being used for more than one percentile.
* A percentile calculated using the nearest-rank method will always be a member of the original ordered list.
* The 100th percentile is defined to be the largest value in the ordered list.
The linear interpolation between closest ranks method
An alternative to rounding used in many applications is to uselinear interpolation
In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points.
Linear interpolation between two known points
If the two known poin ...
between adjacent ranks.
Commonalities between the variants of this method
All of the following variants have the following in common. Given theorder statistics
In statistics, the ''k''th order statistic of a statistical sample is equal to its ''k''th-smallest value. Together with rank statistics, order statistics are among the most fundamental tools in non-parametric statistics and inference.
Importa ...
:
we seek a linear interpolation function that passes through the points . This is simply accomplished by
:
where uses the floor function
In mathematics and computer science, the floor function is the function that takes as input a real number , and gives as output the greatest integer less than or equal to , denoted or . Similarly, the ceiling function maps to the least int ...
to represent the integral part of positive , whereas uses the mod function
In computing, the modulo operation returns the remainder or signed remainder of a division, after one number is divided by another (called the '' modulus'' of the operation).
Given two positive numbers and , modulo (often abbreviated as ) is th ...
to represent its fractional part (the remainder after division by 1). (Note that, though at the endpoint , is undefined, it does not need to be because it is multiplied by .) As we can see, is the continuous version of the subscript , linearly interpolating between adjacent nodes.
There are two ways in which the variant approaches differ. The first is in the linear relationship between the ''rank'' , the ''percent rank'' , and a constant that is a function of the sample size :
:
There is the additional requirement that the midpoint of the range , corresponding to the median, occur at :
:
and our revised function now has just one degree of freedom, looking like this:
:
The second way in which the variants differ is in the definition of the function near the margins of the