Omar Khayam on:
[Wikipedia]
[Google]
[Amazon]
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a
 Khayyam's boyhood was spent in Nishapur, a leading metropolis under the
Khayyam's boyhood was spent in Nishapur, a leading metropolis under the

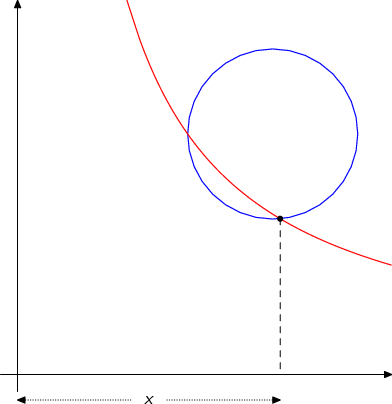 Rashed and Vahabzadeh (2000) have argued that because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered the precursor of Descartes in the invention of
Rashed and Vahabzadeh (2000) have argued that because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered the precursor of Descartes in the invention of
 In 1074–5, Omar Khayyam was commissioned by Sultan Malik-Shah to build an observatory at Isfahan and reform the
In 1074–5, Omar Khayyam was commissioned by Sultan Malik-Shah to build an observatory at Isfahan and reform the
 The earliest allusion to Omar Khayyam's poetry is from the historian
The earliest allusion to Omar Khayyam's poetry is from the historian  There are occasional quotes of verses attributed to Omar in texts attributed to authors of the 13th and 14th centuries, but these are of doubtful authenticity, so that skeptical scholars point out that the entire tradition may be
There are occasional quotes of verses attributed to Omar in texts attributed to authors of the 13th and 14th centuries, but these are of doubtful authenticity, so that skeptical scholars point out that the entire tradition may be
 The quatrain by Omar Khayyam known as "The Moving Finger", in the form of its translation by the English poet Edward FitzGerald (poet), Edward Fitzgerald is one of the most popular quatrains in the Anglosphere. It reads:
The title of the novel "The Moving Finger" written by Agatha Christie and published in 1942 was inspired by this quatrain of the translation of ''
The quatrain by Omar Khayyam known as "The Moving Finger", in the form of its translation by the English poet Edward FitzGerald (poet), Edward Fitzgerald is one of the most popular quatrains in the Anglosphere. It reads:
The title of the novel "The Moving Finger" written by Agatha Christie and published in 1942 was inspired by this quatrain of the translation of ''
File:005-a-Ruby-kindles-in-the-vine-810x1146.jpg, "A Ruby kindles in the vine", illustration for FitzGerald's ''
PDF version
Umar Khayyam
in the ''Stanford Encyclopedia of Philosophy''
The illustrated Rubáiyát of Omar Khayyám
at Internet Archive. {{DEFAULTSORT:Khayyam, Omar Omar Khayyam, 1048 births 1131 deaths 11th-century Iranian astronomers 11th-century Persian-language poets 12th-century astronomers 12th-century Persian-language writers 12th-century Iranian mathematicians 12th-century Persian-language poets Algebra Mathematicians from Nishapur 12th-century Iranian astronomers 11th-century Persian-language writers Iranian philosophers Persian physicists Persian spiritual writers Philosophers from Nishapur Scholars from the Seljuk Empire Poets from the Seljuk Empire
polymath
A polymath ( el, πολυμαθής, , "having learned much"; la, homo universalis, "universal human") is an individual whose knowledge spans a substantial number of subjects, known to draw on complex bodies of knowledge to solve specific pro ...
, known for his contributions to mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest ...
, philosophy
Philosophy (from , ) is the systematized study of general and fundamental questions, such as those about existence, reason, knowledge, values, mind, and language. Such questions are often posed as problems to be studied or resolved. Some ...
, and Persian poetry
Persian literature ( fa, ادبیات فارسی, Adabiyâte fârsi, ) comprises oral compositions and written texts in the Persian language and is one of the world's oldest literatures. It spans over two-and-a-half millennia. Its sources h ...
. He was born in Nishapur
Nishapur or officially Romanized as Neyshabur ( fa, ;Or also "نیشاپور" which is closer to its original and historic meaning though it is less commonly used by modern native Persian speakers. In Persian poetry, the name of this city is wr ...
, the initial capital
Capital may refer to:
Common uses
* Capital city, a municipality of primary status
** List of national capital cities
* Capital letter, an upper-case letter Economics and social sciences
* Capital (economics), the durable produced goods used f ...
of the Seljuk Empire
The Great Seljuk Empire, or the Seljuk Empire was a high medieval, culturally Turco-Persian tradition, Turko-Persian, Sunni Islam, Sunni Muslim empire, founded and ruled by the Qiniq (tribe), Qïnïq branch of Oghuz Turks. It spanned a total are ...
. As a scholar, he was contemporary with the rule of the Seljuk dynasty
The Seljuk dynasty, or Seljukids ( ; fa, سلجوقیان ''Saljuqian'', alternatively spelled as Seljuqs or Saljuqs), also known as Seljuk Turks, Seljuk Turkomans "The defeat in August 1071 of the Byzantine emperor Romanos Diogenes
by the Turk ...
around the time of the First Crusade
The First Crusade (1096–1099) was the first of a series of religious wars, or Crusades, initiated, supported and at times directed by the Latin Church in the medieval period. The objective was the recovery of the Holy Land from Islamic ru ...
.
As a mathematician, he is most notable for his work on the classification and solution of cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s, where he provided geometric solutions by the intersection of conics
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a speci ...
. Khayyam also contributed to the understanding of the parallel axiom.Struik, D. (1958). "Omar Khayyam, mathematician". ''The Mathematics Teacher'', 51(4), 280–285. As an astronomer, he calculated the duration of the solar year with remarkable precision and accuracy, and designed the Jalali calendar
The Jalali calendar is a solar calendar, was compiled during the reign of Jalaluddin Malik-Shah I of Seljuk by the order of Nizam al-Mulk and the place of observation were the cities of Isfahan (the capital of the Seljuks), Rey, and Nishapur. Vari ...
, a solar calendar
A solar calendar is a calendar whose dates indicate the season or almost equivalently the apparent position of the Sun relative to the stars. The Gregorian calendar, widely accepted as a standard in the world, is an example of a solar calendar.
T ...
with a very precise 33-year intercalation cycle''The Cambridge History of Iran'', Volume 4. Cambridge University Press (1975): Richard Nelson Frye that provided the basis for the Persian calendar
The Iranian calendars or Iranian chronology ( fa, گاهشماری ایرانی, ) are a succession of calendars invented or used for over two millennia in Iran, also known as Persia. One of the longest chronological records in human history, ...
that is still in use after nearly a millennium.
There is a tradition of attributing poetry
Poetry (derived from the Greek ''poiesis'', "making"), also called verse, is a form of literature that uses aesthetic and often rhythmic qualities of language − such as phonaesthetics, sound symbolism, and metre − to evoke meanings i ...
to Omar Khayyam, written in the form of quatrain
A quatrain is a type of stanza, or a complete poem, consisting of four lines.
Existing in a variety of forms, the quatrain appears in poems from the poetic traditions of various ancient civilizations including Persia, Ancient India, Ancient Greec ...
s ('' rubāʿiyāt'' ). This poetry became widely known to the English-reading world in a translation by Edward FitzGerald (''Rubaiyat of Omar Khayyam
''Rubáiyát of Omar Khayyám'' is the title that Edward FitzGerald gave to his 1859 translation from Persian to English of a selection of quatrains (') attributed to Omar Khayyam (1048–1131), dubbed "the Astronomer-Poet of Persia".
Altho ...
'', 1859), which enjoyed great success in the Orientalism
In art history, literature and cultural studies, Orientalism is the imitation or depiction of aspects in the Eastern world. These depictions are usually done by writers, designers, and artists from the Western world. In particular, Orientalist p ...
of the ''fin de siècle
() is a French term meaning "end of century,” a phrase which typically encompasses both the meaning of the similar English idiom "turn of the century" and also makes reference to the closing of one era and onset of another. Without context ...
''.
Life
Omar Khayyam was born, of KhorasaniPersian
Persian may refer to:
* People and things from Iran, historically called ''Persia'' in the English language
** Persians, the majority ethnic group in Iran, not to be conflated with the Iranic peoples
** Persian language, an Iranian language of the ...
ancestry, in Nishapur in 1048. In medieval Persian texts he is usually simply called ''Omar Khayyam''. Although open to doubt, it has often been assumed that his forebears followed the trade of tent-making, since ''Khayyam'' means ''tent-maker'' in Arabic.Boyle, J. A., Omar Khayyam: astronomer, mathematician, and poet, Bulletin of the John Rylands Library. 1969; 52(1):30–45. The historian Bayhaqi Bayhaqi (meaning "from Bayhaq") is a surname. Notable people with the surname include:
*Ahmad Bayhaqi (994–1066), Persian Islamic scholar
*Abolfazl Beyhaqi (995–1077), Persian secretary, historian, and author
*Abu'l-Hasan Bayhaqi
Zahir al-Din ...
, who was personally acquainted with Omar, provides the full details of his horoscope: "he was Gemini, the sun and Mercury being in the ascendant ...E. D. R., & H. A. R. G. (1929). The Earliest Account of 'Umar Khayyam. Bulletin of the School of Oriental Studies, University of London, 5(3), 467–473. This was used by modern scholars to establish his date of birth as 18 May 1048.
 Khayyam's boyhood was spent in Nishapur, a leading metropolis under the
Khayyam's boyhood was spent in Nishapur, a leading metropolis under the Great Seljuq Empire
The Great Seljuk Empire, or the Seljuk Empire was a high medieval, culturally Turco-Persian tradition, Turko-Persian, Sunni Islam, Sunni Muslim empire, founded and ruled by the Qiniq (tribe), Qïnïq branch of Oghuz Turks. It spanned a total are ...
,"The Tomb of Omar Khayyâm", George Sarton, ''Isis'', Vol. 29, No. 1 (Jul. 1938), 15.Edward FitzGerald, ''Rubaiyat of Omar Khayyam'', Ed. Christopher Decker, (University of Virginia Press, 1997), xv; "The Seljuq Turks had invaded the province of Khorasan in the 1030s, and the city of Nishapur surrendered to them voluntarily in 1038. Thus Omar Khayyam grew to maturity during the first of the several alien dynasties that would rule Iran until the twentieth century.". and it had been a major center of the Zoroastrian religion
Zoroastrianism is an Iranian religion and one of the world's oldest organized faiths, based on the teachings of the Iranian-speaking prophet Zoroaster. It has a dualistic cosmology of good and evil within the framework of a monotheistic ...
.Mehdi Aminrazavi, ''The Wine of Wisdom: The Life, Poetry and Philosophy of Omar Khayyam'', Oneworld Publications
Oneworld Publications is a British independent publishing firm founded in 1986 by Novin Doostdar and Juliet Mabey originally to publish accessible non-fiction by experts and academics for the general market.
(2007) His full name, as it appears in the Arabic sources, was ''Abu’l Fath Omar ibn Ibrahim al-Khayyam''. His gifts were recognized by his early tutors who sent him to study under Imam Muwaffaq Nishaburi, the greatest teacher of the Khorasan region who tutored the children of the highest nobility. Omar made a great friendship with him through the years. Khayyam was also taught by the Zoroastrian mathematician, Abu Hassan Bahmanyar bin Marzban. After studying science, philosophy, mathematics and astronomy at Nishapur, about the year 1068 he traveled to the province of Bukhara
Bukhara (Uzbek language, Uzbek: /, ; tg, Бухоро, ) is the List of cities in Uzbekistan, seventh-largest city in Uzbekistan, with a population of 280,187 , and the capital of Bukhara Region.
People have inhabited the region around Bukhara ...
, where he frequented the renowned library of the Ark
Ark or ARK may refer to:
Biblical narratives and religion Hebrew word ''teva''
* Noah's Ark, a massive vessel said to have been built to save the world's animals from a flood
* Ark of bulrushes, the boat of the infant Moses
Hebrew ''aron''
* ...
. In about 1070 he moved to Samarkand
fa, سمرقند
, native_name_lang =
, settlement_type = City
, image_skyline =
, image_caption = Clockwise from the top:Registan square, Shah-i-Zinda necropolis, Bibi-Khanym Mosque, view inside Shah-i-Zinda, ...
, where he started to compose his famous treatise on algebra under the patronage of Abu Tahir Abd al-Rahman ibn ʿAlaq, the governor and chief judge
A chief judge (also known as presiding judge, president judge or principal judge) is the highest-ranking or most senior member of a lower court or circuit court with more than one judge. According to the Federal judiciary of the United States, th ...
of the city.Boris A. Rosenfeld «Umar al-Khayyam» in Helaine Selin
Helaine Selin (born 1946) is an American librarian, historian of science, author and the editor of several bestselling books.
Career
Selin attended Binghamton University, where she earned her bachelor's degree. She received her MLS from SUNY Alb ...
, ''Encyclopaedia of the History of Science, Technology, and Medicine in Non-Western Cultures'', Springer-Verlag, 2008, p. 2175-2176 Omar Khayyam was kindly received by the Karakhanid ruler Shams al-Mulk Nasr
Shams al-Mulk Nasr was a Karakhanid ruler in Transoxiana from 1068 to 1080. He was one of the greatest rulers of the dynasty.
Biography
He was the son of Böritigin, a Karakhanid ruler from the western branch of the family, known as the "Alids ...
, who according to Bayhaqi, would "show him the greatest honour, so much so that he would seat mar
Mar, mar or MAR may refer to:
Culture
* Mar or Mor, an honorific in Syriac
* Earl of Mar, an earldom in Scotland
* MAA (singer) (born 1986), Japanese
* Marathi language, by ISO 639-2 language code
* March, as an abbreviation for the third mon ...
beside him on his throne
A throne is the seat of state of a potentate or dignitary, especially the seat occupied by a sovereign on state occasions; or the seat occupied by a pope or bishop on ceremonial occasions. "Throne" in an abstract sense can also refer to the monar ...
".
In 1073–4 peace was concluded with Sultan
Sultan (; ar, سلطان ', ) is a position with several historical meanings. Originally, it was an Arabic abstract noun meaning "strength", "authority", "rulership", derived from the verbal noun ', meaning "authority" or "power". Later, it ...
Malik-Shah I
Jalāl al-Dawla Mu'izz al-Dunyā Wa'l-Din Abu'l-Fatḥ ibn Alp Arslān (8 August 1055 – 19 November 1092, full name: fa, ), better known by his regnal name of Malik-Shah I ( fa, ), was the third sultan of the Great Seljuk Empire from 1072 to ...
who had made incursions into Karakhanid dominions. Khayyam entered the service of Malik-Shah in 1074–5 when he was invited by the Grand Vizier
Grand vizier ( fa, وزيرِ اعظم, vazîr-i aʾzam; ota, صدر اعظم, sadr-ı aʾzam; tr, sadrazam) was the title of the effective head of government of many sovereign states in the Islamic world. The office of Grand Vizier was first ...
Nizam al-Mulk
Abu Ali Hasan ibn Ali Tusi (April 10, 1018 – October 14, 1092), better known by his honorific title of Nizam al-Mulk ( fa, , , Order of the Realm) was a Persian scholar, jurist, political philosopher and Vizier of the Seljuk Empire. Rising fro ...
to meet Malik-Shah in the city of Marv. Khayyam was subsequently commissioned to set up an observatory in Isfahan
Isfahan ( fa, اصفهان, Esfahân ), from its Achaemenid empire, ancient designation ''Aspadana'' and, later, ''Spahan'' in Sassanian Empire, middle Persian, rendered in English as ''Ispahan'', is a major city in the Greater Isfahan Regio ...
and lead a group of scientists in carrying out precise astronomical observations aimed at the revision of the Persian calendar. The undertaking began probably in 1076 and ended in 1079 when Omar Khayyam and his colleagues concluded their measurements of the length of the year, reporting it as 365.24219858156 days. Given that the length of the year is changing in the sixth decimal place over a person's lifetime, this is outstandingly accurate. For comparison the length of the year at the end of the 19th century was 365.242196 days, while today it is 365.242190 days.
After the death of Malik-Shah and his vizier (murdered, it is thought, by the Ismaili
Isma'ilism ( ar, الإسماعيلية, al-ʾIsmāʿīlīyah) is a branch or sub-sect of Shia Islam. The Isma'ili () get their name from their acceptance of Imam Isma'il ibn Jafar as the appointed spiritual successor (imām) to Ja'far al-Sa ...
order of Assassins
The Order of Assassins or simply the Assassins ( fa, حَشّاشین, Ḥaššāšīn, ) were a Nizārī Ismāʿīlī order and sect of Shīʿa Islam that existed between 1090 and 1275 CE. During that time, they lived in the mountains of P ...
), Omar fell from favor at court, and as a result, he soon set out on his pilgrimage to Mecca. A possible ulterior motive for his pilgrimage reported by Al-Qifti
'Alī ibn Yūsuf al-Qifṭī or Ali Ibn Yusuf the Qifti (of Qift, his home city) (), he was ''Jamāl al-Dīn Abū al-Ḥasan 'Alī ibn Yūsuf ibn Ibrāhīm ibn 'Abd al-Wahid al-Shaybānī'' () (ca. 1172–1248); an Egyptian Arab historian, biog ...
, was a public demonstration of his faith with a view to allaying suspicions of skepticism and confuting the allegations of unorthodoxy (including possible sympathy or adherence to Zoroastrianism) levelled at him by a hostile clergy. He was then invited by the new Sultan Sanjar
Senjer ( fa, ; full name: ''Muizz ad-Dunya wa ad-Din Adud ad-Dawlah Abul-Harith Ahmad Sanjar ibn Malik-Shah'') (''b''. 1085 – ''d''. 8 May 1157) was the Seljuq ruler of Khorasan from 1097 until in 1118,astrologer
Astrology is a range of divinatory practices, recognized as pseudoscientific since the 18th century, that claim to discern information about human affairs and terrestrial events by studying the apparent positions of celestial objects. Dif ...
. He was later allowed to return to Nishapur owing to his declining health. Upon his return, he seems to have lived the life of a recluse.Great Muslim Mathematicians. Penerbit UTM (July 2000): Mohini Mohamed
Omar Khayyam died at the age of 83 in his hometown of Nishapur on 4 December 1131, and he is buried in what is now the Mausoleum of Omar Khayyam. One of his disciples Nizami Aruzi Ahmad ibn Umar ibn Alī, known as Nizamī-i Arūzī-i Samarqandī ( fa, نظامی عروضی) and also Arudi ("The Prosodist"), was a Persian poet and prose writer who flourished between 1110 and 1161. He is particularly famous for his ''Chahar M ...
relates the story that sometime during 1112–3 Khayyam was in Balkh
), named for its green-tiled ''Gonbad'' ( prs, گُنبَد, dome), in July 2001
, pushpin_map=Afghanistan#Bactria#West Asia
, pushpin_relief=yes
, pushpin_label_position=bottom
, pushpin_mapsize=300
, pushpin_map_caption=Location in Afghanistan ...
in the company of Al-Isfizari
Abū Ḥātim al-Muẓaffar al-Isfazārī (Floruit, fl. late 11th or early 12th century) was an Islamic mathematician, astronomer and engineer from Khurasan. According to the historian and geographer Ibn al-Athir and the polymath Qutb al-Din al ...
(one of the scientists who had collaborated with him on the Jalali calendar) when he made a prophecy that "my tomb shall be in a spot where the north wind may scatter roses over it". Four years after his death, Aruzi located his tomb in a cemetery in a then large and well-known quarter of Nishapur on the road to Marv. As it had been foreseen by Khayyam, Aruzi found the tomb situated at the foot of a garden-wall over which pear trees and peach trees had thrust their heads and dropped their flowers so that his tombstone was hidden beneath them.
Mathematics
Khayyam was famous during his life as amathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
. His surviving mathematical works include: ''A commentary on the difficulties concerning the postulates of Euclid's Elements'' (, completed in December 1077), ''On the division of a quadrant of a circle'' (, undated but completed prior to the treatise on algebra), and ''On proofs for problems concerning Algebra'' (, most likely completed in 1079). He furthermore wrote a treatise on the binomial theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the polynomial into a sum involving terms of the form , where the ...
and extracting the nth root of natural numbers, which has been lost.
Theory of parallels
A part of Khayyam's commentary on Euclid's Elements deals with the parallel axiom. The treatise of Khayyam can be considered the first treatment of the axiom not based onpetitio principii
In classical rhetoric and logic, begging the question or assuming the conclusion (Latin: ') is an informal fallacy that occurs when an argument's premises assume the truth of the conclusion, instead of supporting it.
For example:
* "Green is ...
, but on a more intuitive postulate. Khayyam refutes the previous attempts by other mathematicians to ''prove'' the proposition, mainly on grounds that each of them had postulated something that was by no means easier to admit than the Fifth Postulate itself. Drawing upon Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
's views, he rejects the usage of movement in geometry and therefore dismisses the different attempt by Al-Haytham
Ḥasan Ibn al-Haytham, Latinized as Alhazen (; full name ; ), was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the prin ...
.. Excerpt: ''In some sense, his treatment was better than ibn al-Haytham's because he explicitly formulated a new postulate to replace Euclid's rather than have the latter hidden in a new definition.'' Unsatisfied with the failure of mathematicians to prove Euclid's statement from his other postulates, Omar tried to connect the axiom with the Fourth Postulate, which states that all right angles are equal to one another.
Khayyam was the first to consider the three distinct cases of acute, obtuse, and right angle for the summit angles of a Khayyam-Saccheri quadrilateral. After proving a number of theorems about them, he showed that Postulate V follows from the right angle hypothesis, and refuted the obtuse and acute cases as self-contradictory. His elaborate attempt to prove the parallel postulate was significant for the further development of geometry, as it clearly shows the possibility of non-Euclidean geometries. The hypotheses of acute, obtuse, and right angles are now known to lead respectively to the non-Euclidean hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or Bolyai– Lobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P'' ...
of Gauss-Bolyai-Lobachevsky, to that of Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a ''Riemannian metric'', i.e. with an inner product on the tangent space at each point that varies smoothly from point to poin ...
, and to Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
.

Tusi
''Tusi'', often translated as "headmen" or "chieftains", were hereditary tribal leaders recognized as imperial officials by the Yuan, Ming, and Qing dynasties of China, and the Later Lê and Nguyễn dynasties of Vietnam. They ruled certain et ...
's commentaries on Khayyam's treatment of parallels made its way to Europe. John Wallis
John Wallis (; la, Wallisius; ) was an English clergyman and mathematician who is given partial credit for the development of infinitesimal calculus. Between 1643 and 1689 he served as chief cryptographer for Parliament and, later, the royal ...
, professor of geometry at Oxford, translated Tusi's commentary into Latin. Jesuit geometer Girolamo Saccheri, whose work (''euclides ab omni naevo vindicatus'', 1733) is generally considered the first step in the eventual development of non-Euclidean geometry
In mathematics, non-Euclidean geometry consists of two geometries based on axioms closely related to those that specify Euclidean geometry. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geo ...
, was familiar with the work of Wallis. The American historian of mathematics David Eugene Smith
David Eugene Smith (January 21, 1860 – July 29, 1944) was an American mathematician, educator, and editor.
Education and career
David Eugene Smith is considered one of the founders of the field of mathematics education. Smith was born in Cortl ...
mentions that Saccheri "used the same lemma as the one of Tusi, even lettering the figure in precisely the same way and using the lemma for the same purpose". He further says that "Tusi distinctly states that it is due to Omar Khayyam, and from the text, it seems clear that the latter was his inspirer."
The real number concept
This treatise on Euclid contains another contribution dealing with the theory of proportions and with the compounding of ratios. Khayyam discusses the relationship between the concept of ratio and the concept of number and explicitly raises various theoretical difficulties. In particular, he contributes to the theoretical study of the concept ofirrational number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integ ...
. Displeased with Euclid's definition of equal ratios, he redefined the concept of a number by the use of a continuous fraction as the means of expressing a ratio. Rosenfeld and Youschkevitch (1973) argue that "by placing irrational quantities and numbers on the same operational scale, hayyambegan a true revolution in the doctrine of number." Likewise, it was noted by D. J. Struik that Omar was "on the road to that extension of the number concept which leads to the notion of the real number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every real ...
."
Geometric algebra
 Rashed and Vahabzadeh (2000) have argued that because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered the precursor of Descartes in the invention of
Rashed and Vahabzadeh (2000) have argued that because of his thoroughgoing geometrical approach to algebraic equations, Khayyam can be considered the precursor of Descartes in the invention of analytic geometry
In classical mathematics, analytic geometry, also known as coordinate geometry or Cartesian geometry, is the study of geometry using a coordinate system. This contrasts with synthetic geometry.
Analytic geometry is used in physics and engineerin ...
.Cooper, G. (2003). ''Journal of the American Oriental Society'', 123(1), 248–249. In ''The Treatise on the Division of a Quadrant of a Circle'' Khayyam applied algebra to geometry. In this work, he devoted himself mainly to investigating whether it is possible to divide a circular quadrant into two parts such that the line segments projected from the dividing point to the perpendicular diameters of the circle form a specific ratio. His solution, in turn, employed several curve constructions that led to equations containing cubic and quadratic terms.
The solution of cubic equations
Khayyam seems to have been the first to conceive a general theory of cubic equations and the first to geometrically solve every type of cubic equation, so far as positive roots are concerned. The treatise on algebra contains his work oncubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s. It is divided into three parts: (i) equations which can be solved with compass and straight edge, (ii) equations which can be solved by means of conic section
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a specia ...
s, and (iii) equations which involve the inverse of the unknown.
Khayyam produced an exhaustive list of all possible equations involving lines, squares, and cubes. He considered three binomial equations, nine trinomial equations, and seven tetranomial equations. For the first and second degree polynomials, he provided numerical solutions by geometric construction. He concluded that there are fourteen different types of cubics that cannot be reduced to an equation of a lesser degree. For these he could not accomplish the construction of his unknown segment with compass and straight edge. He proceeded to present geometric solutions to all types of cubic equations using the properties of conic sections.Deborah A. Kent, & David J. Muraki (2016). "A Geometric Solution of a Cubic by Omar Khayyam … in Which Colored Diagrams Are Used Instead of Letters for the Greater Ease of Learners". ''The American Mathematical Monthly'', 123(2), 149–160. The prerequisite lemmas for Khayyam's geometrical proof include Euclid VI, Prop 13, and Apollonius II, Prop 12. The positive root of a cubic equation was determined as the abscissa
In common usage, the abscissa refers to the (''x'') coordinate and the ordinate refers to the (''y'') coordinate of a standard two-dimensional graph.
The distance of a point from the y-axis, scaled with the x-axis, is called abscissa or x coo ...
of a point of intersection of two conics, for instance, the intersection of two parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descript ...
s, or the intersection of a parabola and a circle, etc.Kennedy, E. (1958). "Omar Khayyam". ''The Mathematics Teacher'', Vol. 59, No. 2 (1966), pp. 140–142. However, he acknowledged that the arithmetic problem of these cubics was still unsolved, adding that "possibly someone else will come to know it after us". This task remained open until the sixteenth century, where algebraic solution of the cubic equation was found in its generality by Cardano, Del Ferro, and Tartaglia in Renaissance Italy
The Italian Renaissance ( it, Rinascimento ) was a period in Italian history covering the 15th and 16th centuries. The period is known for the initial development of the broader Renaissance culture that spread across Europe and marked the trans ...
.
In effect, Khayyam's work is an effort to unify algebra and geometry.The Mathematics Teacher, 25(4), 238–241. (1932). This particular geometric solution of cubic equations has been further investigated by M. Hachtroudi and extended to solving fourth-degree equations. Although similar methods had appeared sporadically since Menaechmus :''There is also a Menaechmus in Plautus' play, ''The Menaechmi''.''
Menaechmus ( el, Μέναιχμος, 380–320 BC) was an ancient Greek mathematician, geometer and philosopher born in Alopeconnesus or Prokonnesos in the Thracian Chersonese, wh ...
, and further developed by the 10th-century mathematician Abu al-Jud, Khayyam's work can be considered the first systematic study and the first exact method of solving cubic equations. Mathematical Masterpieces: Further Chronicles by the Explorers, p. 92 The mathematician Woepcke (1851) who offered translations of Khayyam's algebra into French praised him for his "power of generalization and his rigorously systematic procedure."E. H. Whinfield, ''The Quatrains of Omar Khayyam'', Psychology Press (2000)
Binomial theorem and extraction of roots
In his algebraic treatise, Khayyam alludes to a book he had written on the extraction of the th root of the numbers using a law he had discovered which did not depend on geometric figures. This book was most likely titled ''The difficulties of arithmetic'' (), and is not extant. Based on the context, some historians of mathematics such as D. J. Struik, believe that Omar must have known the formula for the expansion of the binomial , where is a positive integer. The case of power 2 is explicitly stated in Euclid's elements and the case of at most power 3 had been established by Indian mathematicians. Khayyam was themathematician
A mathematician is someone who uses an extensive knowledge of mathematics in their work, typically to solve mathematical problems.
Mathematicians are concerned with numbers, data, quantity, structure, space, models, and change.
History
On ...
who noticed the importance of a general binomial theorem. The argument supporting the claim that Khayyam had a general binomial theorem is based on his ability to extract roots. One of Khayyam's predecessors, Al-Karaji, had already discovered the triangular arrangement of the coefficients of binomial expansions that Europeans later came to know as Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
; Khayyam popularized this triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index. That is, the ''i''th row contains only ''i'' elements.
Examples
Notable ...
in Iran, so that it is now known as Omar Khayyam's triangle.
Astronomy
Persian calendar
The Iranian calendars or Iranian chronology ( fa, گاهشماری ایرانی, ) are a succession of calendars invented or used for over two millennia in Iran, also known as Persia. One of the longest chronological records in human history, ...
. There was a panel of eight scholars working under the direction of Khayyam to make large-scale astronomical observations and revise the astronomical tables. Recalibrating the calendar fixed the first day of the year at the exact moment of the passing of the Sun's center across vernal equinox. This marks the beginning of spring or Nowrūz, a day in which the Sun enters the first degree of Aries
Aries may refer to:
*Aries (astrology), an astrological sign
*Aries (constellation), a constellation of stars in the zodiac
Arts, entertainment and media
* ''Aries'' (album), by Luis Miguel, 1993
* ''Aries'' (EP), by Alice Chater, 2020
* "Aries" ...
before noon.
The resultant calendar was named in Malik-Shah's honor as the Jalālī calendar, and was inaugurated on 15 March 1079. The observatory
An observatory is a location used for observing terrestrial, marine, or celestial events. Astronomy, climatology/meteorology, geophysical, oceanography and volcanology are examples of disciplines for which observatories have been constructed. His ...
itself was disused after the death of Malik-Shah in 1092.
The Jalālī calendar was a true solar calendar
A solar calendar is a calendar whose dates indicate the season or almost equivalently the apparent position of the Sun relative to the stars. The Gregorian calendar, widely accepted as a standard in the world, is an example of a solar calendar.
T ...
where the duration of each month is equal to the time of the passage of the Sun across the corresponding sign of the Zodiac
The zodiac is a belt-shaped region of the sky that extends approximately 8° north or south (as measured in celestial latitude) of the ecliptic, the Sun path, apparent path of the Sun across the celestial sphere over the course of the year. ...
. The calendar reform introduced a unique 33-year intercalation cycle. As indicated by the works of Khazini, Khayyam's group implemented an intercalation system based on quadrennial and quinquennial leap years
A leap year (also known as an intercalary year or bissextile year) is a calendar year that contains an additional day (or, in the case of a lunisolar calendar, a month) added to keep the calendar year synchronized with the astronomical year or s ...
. Therefore, the calendar consisted of 25 ordinary years that included 365 days, and 8 leap years that included 366 days. The calendar remained in use across Greater Iran
Greater Iran ( fa, ایران بزرگ, translit=Irān-e Bozorg) refers to a region covering parts of Western Asia, Central Asia, South Asia, Xinjiang, and the Caucasus, where both Culture of Iran, Iranian culture and Iranian langua ...
from the 11th to the 20th centuries. In 1911 the Jalali calendar became the official national calendar of Qajar Iran
Qajar Iran (), also referred to as Qajar Persia, the Qajar Empire, '. Sublime State of Persia, officially the Sublime State of Iran ( fa, دولت علیّه ایران ') and also known then as the Guarded Domains of Iran ( fa, ممالک م ...
. In 1925 this calendar was simplified and the names of the months were modernized, resulting in the modern Iranian calendar. The Jalali calendar is more accurate than the Gregorian calendar
The Gregorian calendar is the calendar used in most parts of the world. It was introduced in October 1582 by Pope Gregory XIII as a modification of, and replacement for, the Julian calendar. The principal change was to space leap years dif ...
of 1582, with an error of one day accumulating over 5,000 years, compared to one day every 3,330 years in the Gregorian calendar.
Moritz Cantor
Moritz Benedikt Cantor (23 August 1829 – 10 April 1920) was a German historian of mathematics.
Biography
Cantor was born at Mannheim. He came from a Sephardi Jewish family that had emigrated to the Netherlands from Portugal
Portugal, off ...
considered it the most perfect calendar ever devised.
One of his pupils Nizami Aruzi of Samarcand relates that Khayyam apparently did not have a belief in astrology and divination: "I did not observe that he (''scil.'' Omar Khayyam) had any great belief in astrological predictions, nor have I seen or heard of any of the great cientistswho had such belief." While working for Sultan Sanjar as an astrologer he was asked to predict the weather – a job that he apparently did not do well. George Saliba (2002) explains that the term , used in various sources in which references to Omar's life and work could be found, has sometimes been incorrectly translated to mean astrology. He adds: "from at least the middle of the tenth century, according to Farabi
Abu Nasr Muhammad Al-Farabi ( fa, ابونصر محمد فارابی), ( ar, أبو نصر محمد الفارابي), known in the West as Alpharabius; (c. 872 – between 14 December, 950 and 12 January, 951)PDF version was a renowned early Isla ...
's enumeration of the sciences, that this science, , was already split into two parts, one dealing with astrology and the other with theoretical mathematical astronomy."
Other works
He has a short treatise devoted toArchimedes' principle
Archimedes' principle (also spelled Archimedes's principle) states that the upward buoyant force that is exerted on a body immersed in a fluid, whether fully or partially, is equal to the weight of the fluid that the body displaces. Archimede ...
(in full title, ''On the Deception of Knowing the Two Quantities of Gold and Silver in a Compound Made of the Two''). For a compound of gold adulterated with silver, he describes a method to measure more exactly the weight per capacity of each element. It involves weighing the compound both in air and in water, since weights are easier to measure exactly than volumes. By repeating the same with both gold and silver one finds exactly how much heavier than water gold, silver and the compound were. This treatise was extensively examined by Eilhard Wiedemann Eilhard Ernst Gustav Wiedemann (1 August 1852, in Berlin – 7 January 1928, in Erlangen) was a German physicist and historian of science. He was the son of physicist Gustav Heinrich Wiedemann (1826–1899), and an older brother to Egyptologist Alf ...
who believed that Khayyam's solution was more accurate and sophisticated than that of Khazini and Al-Nayrizi
Abū’l-‘Abbās al-Faḍl ibn Ḥātim al-Nairīzī ( ar, أبو العباس الفضل بن حاتم النيريزي, la, Anaritius, Nazirius, c. 865–922) was a Persian mathematician and astronomer from Nayriz, Fars Province, Iran.
He fl ...
who also dealt with the subject elsewhere.
Another short treatise is concerned with music theory
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
in which he discusses the connection between music and arithmetic. Khayyam's contribution was in providing a systematic classification of musical scales, and discussing the mathematical relationship among notes, minor, major and tetrachords.
Poetry
 The earliest allusion to Omar Khayyam's poetry is from the historian
The earliest allusion to Omar Khayyam's poetry is from the historian Imad ad-Din al-Isfahani
Muhammad ibn Hamed Isfahani (1125 – 20 June 1201) ( fa, محمد ابن حامد اصفهانی), more popularly known as Imad ad-din al-Isfahani ( fa, عماد الدین اصفهانی) ( ar, عماد الدين الأصفهاني), was ...
, a younger contemporary of Khayyam, who explicitly identifies him as both a poet and a scientist (, 1174).Ali Dashti (translated by L. P. Elwell-Sutton), ''In Search of Omar Khayyam'', Routledge Library Editions: Iran (2012) One of the earliest specimens of Omar Khayyam's Rubiyat is from Fakhr al-Din Razi. In his work (ca. 1160), he quotes one of his poems (corresponding to quatrain LXII of FitzGerald's first edition). Daya in his writings (, ca. 1230) quotes two quatrains, one of which is the same as the one already reported by Razi. An additional quatrain is quoted by the historian Juvayni (, ca. 1226–1283). In 1340 Jajarmi includes thirteen quatrains of Khayyam in his work containing an anthology of the works of famous Persian poets (), two of which have hitherto been known from the older sources.Edward Denison Ross, ''Omar Khayyam'', Bulletin of the School Of Oriental Studies London Institution (1927) A comparatively late manuscript is the Bodleian
The Bodleian Library () is the main research library of the University of Oxford, and is one of the oldest libraries in Europe. It derives its name from its founder, Sir Thomas Bodley. With over 13 million printed items, it is the second- ...
MS. Ouseley 140, written in Shiraz
Shiraz (; fa, شیراز, Širâz ) is the List of largest cities of Iran, fifth-most-populous city of Iran and the capital of Fars province, Fars Province, which has been historically known as Pars (Sasanian province), Pars () and Persis. As o ...
in 1460, which contains 158 quatrains on 47 folia. The manuscript belonged to William Ouseley
Sir William Ouseley HFRSE FSAScot (1767September, 1842), was a British orientalist.
Early life
Ouseley was born in Monmouthshire, the eldest son of Captain Ralph Ouseley and his wife Elizabeth (born Holland). He was tutored at home in the c ...
(1767–1842) and was purchased by the Bodleian Library in 1844.pseudepigraphic
Pseudepigrapha (also anglicized as "pseudepigraph" or "pseudepigraphs") are falsely attributed works, texts whose claimed author is not the true author, or a work whose real author attributed it to a figure of the past.Bauckham, Richard; "Pseu ...
.
Hans Heinrich Schaeder
Heinz Heinrich Schaeder (31 January 1896 – 13 March 1957) was a German Orientalist and Iranologist.
Life
Heinz Heinrich Schaeder was born in Göttingen, Germany on 31 January 1896. He was the son of theologist Erich Schaeder, brother of his ...
in 1934 commented that the name of Omar Khayyam "is to be struck out from the history of Persian literature" due to the lack of any material that could confidently be attributed to him.
De Blois (2004) presents a bibliography of the manuscript tradition, concluding pessimistically that the situation has not changed significantly since Schaeder's time.
Five of the quatrains later attributed to Omar are found as early as 30 years after his death, quoted in ''Sindbad-Nameh
The ''Seven Wise Masters'' (also called the ''Seven Sages'' or ''Seven Wise Men'') is a cycle of stories of Sanskrit, Persian or Hebrew origins.
Story and plot
The Sultan sends his son, the young Prince, to be educated away from the court in th ...
''. While this establishes that these specific verses were in circulation in Omar's time or shortly later, it doesn't imply that the verses must be his. De Blois concludes that at the least the process of attributing poetry to Omar Khayyam appears to have begun already in the 13th century. Edward Granville Browne
Edward Granville Browne FBA (7 February 1862 – 5 January 1926) was a British Iranologist. He published numerous articles and books, mainly in the areas of history and literature.
Life
Browne was born in Stouts Hill, Uley, Gloucestershire, En ...
(1906) notes the difficulty of disentangling authentic from spurious quatrains: "while it is certain that Khayyam wrote many quatrains, it is hardly possible, save in a few exceptional cases, to assert positively that he wrote any of those ascribed to him".
In addition to the Persian quatrains, there are twenty-five Arabic poems attributed to Khayyam which are attested by historians such as al-Isfahani, Shahrazuri
Shams al-Din Muhammad ibn Mahmud Shahrazuri was a 13th-century Muslim physician, historian and philosopher. He was of Kurdish origin. It appears that he was alive in AD 1288. However, it is also said that he died in the same year.
Shahrazuri was ...
(, ca. 1201–1211), Qifti (, 1255), and Hamdallah Mustawfi
Hamdallah Mustawfi Qazvini ( fa, حمدالله مستوفى قزوینی, Ḥamdallāh Mustawfī Qazvīnī; 1281 – after 1339/40) was a Persian official, historian, geographer and poet. He lived during the last era of the Mongol Ilkhanate, and ...
(, 1339).
Boyle
Boyle is an English, Irish and Scottish surname of Gaelic, Anglo-Saxon or Norman origin. In the northwest of Ireland it is one of the most common family names. Notable people with the surname include:
Disambiguation
*Adam Boyle (disambiguation), ...
and Frye Frye is a surname. Notable people with the surname include:
*Channing Frye (born 1983), basketball player
*Charlie Frye (born 1981), football player for the Oakland Raiders
*Don Frye (born 1965), mixed martial arts fighter
*Donna Frye (born 1952), ...
(1975) emphasize that there are a number of other Persian scholars who occasionally wrote quatrains, including Avicenna, Ghazzali, and Tusi. He concludes that it is also possible that for Khayyam poetry was an amusement of his leisure hours: "these brief poems seem often to have been the work of scholars and scientists who composed them, perhaps, in moments of relaxation to edify or amuse the inner circle of their disciples".
The poetry attributed to Omar Khayyam has contributed greatly to his popular fame in the modern period as a direct result of the extreme popularity of the translation of such verses into English by Edward FitzGerald (1859). FitzGerald's ''Rubaiyat of Omar Khayyam
''Rubáiyát of Omar Khayyám'' is the title that Edward FitzGerald gave to his 1859 translation from Persian to English of a selection of quatrains (') attributed to Omar Khayyam (1048–1131), dubbed "the Astronomer-Poet of Persia".
Altho ...
'' contains loose translations of quatrains from the Bodleian manuscript. It enjoyed such success in the fin de siècle
() is a French term meaning "end of century,” a phrase which typically encompasses both the meaning of the similar English idiom "turn of the century" and also makes reference to the closing of one era and onset of another. Without context ...
period that a bibliography compiled in 1929 listed more than 300 separate editions, and many more have been published since.
Philosophy
Khayyam considered himself intellectually to be a student ofAvicenna
Ibn Sina ( fa, ابن سینا; 980 – June 1037 CE), commonly known in the West as Avicenna (), was a Persian polymath who is regarded as one of the most significant physicians, astronomers, philosophers, and writers of the Islamic G ...
.Nasr, S. H., & Aminrazavi, M. (2007). ''Anthology of philosophy in Persia: from Zoroaster to Omar Khayyam''. According to Al-Bayhaqi, he was reading the metaphysics in Avicenna's ''the Book of Healing
''The Book of Healing'' (; ; also known as ) is a scientific and philosophical encyclopedia written by Abu Ali ibn Sīna (aka Avicenna) from medieval Persia, near Bukhara in Maverounnahr. He most likely began to compose the book in 1014, comp ...
'' before he died. There are six philosophical papers believed to have been written by Khayyam. One of them, ''On existence'' (), was written originally in Persian and deals with the subject of existence and its relationship to universals. Another paper, titled ''The necessity of contradiction in the world, determinism and subsistence'' (), is written in Arabic and deals with free will
Free will is the capacity of agents to choose between different possible courses of action unimpeded.
Free will is closely linked to the concepts of moral responsibility, praise, culpability, sin, and other judgements which apply only to actio ...
and determinism
Determinism is a philosophical view, where all events are determined completely by previously existing causes. Deterministic theories throughout the history of philosophy have developed from diverse and sometimes overlapping motives and consi ...
. The titles of his other works are ''On being and necessity'' (), ''The Treatise on Transcendence in Existence'' (), ''On the knowledge of the universal principles of existence'' (), and ''Abridgement concerning natural phenomena'' ().
Religious views
A literal reading of Khayyam's quatrains leads to the interpretation of his philosophic attitude toward life as a combination ofpessimism
Pessimism is a negative mental attitude in which an undesirable outcome is anticipated from a given situation. Pessimists tend to focus on the negatives of life in general. A common question asked to test for pessimism is "Is the glass half empt ...
, nihilism
Nihilism (; ) is a philosophy, or family of views within philosophy, that rejects generally accepted or fundamental aspects of human existence, such as objective truth, knowledge, morality, values, or meaning. The term was popularized by Ivan ...
, Epicureanism
Epicureanism is a system of philosophy founded around 307 BC based upon the teachings of the ancient Greek philosopher Epicurus. Epicureanism was originally a challenge to Platonism. Later its main opponent became Stoicism.
Few writings by Epi ...
, fatalism
Fatalism is a family of related philosophical doctrines that stress the subjugation of all events or actions to fate or destiny, and is commonly associated with the consequent attitude of resignation in the face of future events which are thou ...
, and agnosticism
Agnosticism is the view or belief that the existence of God, of the divine or the supernatural is unknown or unknowable. (page 56 in 1967 edition) Another definition provided is the view that "human reason is incapable of providing sufficient ...
. This view is taken by Iranologists
Iranian studies ( fa, ايرانشناسی '), also referred to as Iranology and Iranistics, is an interdisciplinary field dealing with the research and study of the civilization, history, literature, art and culture of Iranian peoples. It ...
such as Arthur Christensen
Arthur Emanuel Christensen (9 January 1875 – 31 March 1945) was a Danes, Danish Orientalism, orientalist and scholar of Iranian peoples, Iranian philology and Persian literature, folklore. He is best known for his works on the Iranian history, ...
, H. Schaeder, Richard N. Frye
Richard Nelson Frye (January 10, 1920 – March 27, 2014) was an American scholar of Iranian and Central Asian studies, and Aga Khan Professor Emeritus of Iranian Studies at Harvard University. His professional areas of interest were Irania ...
, E. D. Ross,Ross, E. (1898). Al-Musaffariyé: Containing a Recent Contribution to the Study of 'Omar Khayyām. Journal of the Royal Asiatic Society of Great Britain and Ireland, 349–366. E. H. Whinfield and George Sarton
George Alfred Leon Sarton (; 31 August 1884 – 22 March 1956) was a Belgian-born American chemist and historian. He is considered the founder of the discipline of the history of science as an independent field of study. His most influential works ...
. Conversely, the Khayyamic quatrains have also been described as mystical Sufi
Sufism ( ar, ''aṣ-ṣūfiyya''), also known as Tasawwuf ( ''at-taṣawwuf''), is a mystic body of religious practice, found mainly within Sunni Islam but also within Shia Islam, which is characterized by a focus on Islamic spirituality, ...
poetry. In addition to his Persian quatrains, J. C. E. Bowen (1973) mentions that Khayyam's Arabic poems also "express a pessimistic viewpoint which is entirely consonant with the outlook of the deeply thoughtful rationalist philosopher that Khayyam is known historically to have been."J. C. E. Bowen. (1973). The Rubāՙiyyāt of Omar Khayyam: A Critical Assessment of Robert Graves' and Omar Ali Shah's Translation. Iran, 11, 63–73. Edward FitzGerald emphasized the religious skepticism he found in Khayyam. In his preface to the ''Rubáiyát'' he claimed that he "was hated and dreaded by the Sufis", and denied any pretense at divine allegory: "his Wine is the veritable Juice of the Grape: his Tavern, where it was to be had: his ''Saki'', the Flesh and Blood that poured it out for him." Sadegh Hedayat
Sadegh Hedayat ( fa, صادق هدایت ; 17 February 1903 – 9 April 1951) was an Iranian writer and translator. Best known for his novel '' The Blind Owl'', he was one of the earliest Iranian writers to adopt literary modernism in their care ...
is one of the most notable proponents of Khayyam's philosophy as agnostic skepticism, and according to Jan Rypka
Jan Rypka, PhDr., Dr.Sc. (28 May 1886 in Kroměříž – 29 December 1968 in Prague) was a prominent Czech orientalist, translator, professor of Iranology and Turkology at Charles University, Prague.
Jan Rypka was a participant in Ferdowsi ...
(1934), he even considered Khayyam an atheist
Atheism, in the broadest sense, is an absence of belief in the existence of deities. Less broadly, atheism is a rejection of the belief that any deities exist. In an even narrower sense, atheism is specifically the position that there no ...
. Hedayat (1923) states that "while Khayyam believes in the transmutation and transformation of the human body, he does not believe in a separate soul; if we are lucky, our bodily particles would be used in the making of a jug of wine." Omar Khayyam's poetry has been cited in the context of New Atheism
The term ''New Atheism'' was coined by the journalist Gary Wolf (journalist), Gary Wolf in 2006 to describe the positions promoted by some atheists of the twenty-first century. New Atheism advocates the view that superstition, religion and irrat ...
, such as in '' The Portable Atheist'' by Christopher Hitchens
Christopher Eric Hitchens (13 April 1949 – 15 December 2011) was a British-American author and journalist who wrote or edited over 30 books (including five essay collections) on culture, politics, and literature. Born and educated in England, ...
.
Al-Qifti
'Alī ibn Yūsuf al-Qifṭī or Ali Ibn Yusuf the Qifti (of Qift, his home city) (), he was ''Jamāl al-Dīn Abū al-Ḥasan 'Alī ibn Yūsuf ibn Ibrāhīm ibn 'Abd al-Wahid al-Shaybānī'' () (ca. 1172–1248); an Egyptian Arab historian, biog ...
(ca. 1172–1248) appears to confirm this view of Omar's philosophy. In his work ''The History of Learned Men'' he reports that Omar's poems were only outwardly in the Sufi style, but were written with an anti-religious agenda. He also mentions that he was at one point indicted for impiety, but went on a pilgrimage to prove he was pious. The report has it that upon returning to his native city he concealed his deepest convictions and practised a strictly religious life, going morning and evening to the place of worship.
In the context of a piece entitled ''On the Knowledge of the Principles of Existence'', Khayyam endorses the Sufi path. Csillik (1960) suggests the possibility that Omar Khayyam could see in Sufism an ally against orthodox religiosity.Csillik, B. (1960). "The Real 'Omar Khayyām'". Acta Orientalia Academiae Scientiarum Hungaricae, 10(1), 59–77. Retrieved from https://www.jstor.org/stable/23682646 Other commentators do not accept that Omar's poetry has an anti-religious agenda and interpret his references to wine and drunkenness in the conventional metaphorical sense common in Sufism. The French translator J. B. Nicolas held that Omar's constant exhortations to drink wine should not be taken literally, but should be regarded rather in the light of Sufi thought where rapturous intoxication by "wine" is to be understood as a metaphor for the enlightened state or divine rapture of ''baqaa
Baqaa ( ar, بقاء '), with literal meaning of subsistence or permanency, is a term in Sufi philosophy which describes a particular state of life with God, through God, in God, and for God. It is the summit of the mystical manazil, that is, ...
''. The view of Omar Khayyam as a Sufi was defended by Bjerregaard (1915), Idries Shah
Idries Shah (; hi, इदरीस शाह, ps, ادريس شاه, ur, ; 16 June 1924 – 23 November 1996), also known as Idris Shah, né Sayed Idries el- Hashimi (Arabic: سيد إدريس هاشمي) and by the pen name Arko ...
(1999), and Dougan (1991) who attributes the reputation of hedonism to the failings of FitzGerald's translation, arguing that Omar's poetry is to be understood as "deeply esoteric". On the other hand, Iranian experts such as Mohammad Ali Foroughi
Mohammad Ali Foroughi ( fa, محمدعلی فروغی; early August 1877 – 26 or 27 November 1942), also known as Zoka-ol-Molk ( Persian: ذُکاءُالمُلک), was a writer, diplomat and politician who served three terms as Prime Mini ...
and Mojtaba Minovi
Mojtaba Minovi ( fa, مجتبی مینوی; February 1903 Tehran – January 1977, Tehran), was an Iranian historian, literary scholar and professor of Tehran University. He was a participant in the Ferdowsi Millenary celebrations in 1934 in Teh ...
rejected the hypothesis that Omar Khayyam was a Sufi. Foroughi stated that Khayyam's ideas may have been consistent with that of Sufis at times but there is no evidence that he was formally a Sufi
Sufism ( ar, ''aṣ-ṣūfiyya''), also known as Tasawwuf ( ''at-taṣawwuf''), is a mystic body of religious practice, found mainly within Sunni Islam but also within Shia Islam, which is characterized by a focus on Islamic spirituality, ...
. Aminrazavi (2007) states that "Sufi interpretation of Khayyam is possible only by reading into his ''Rubāʿīyyāt'' extensively and by stretching the content to fit the classical Sufi doctrine." Furthermore, Frye (1975) emphasizes that Khayyam was intensely disliked by a number of celebrated Sufi mystics who belonged to the same century. This includes Shams Tabrizi
Shams-i Tabrīzī ( fa, شمس تبریزی) or Shams al-Din Mohammad (1185–1248) was a Persian
*
*
*
* Shafi'ite poet, who is credited as the spiritual instructor of Mewlānā Jalāl ad-Dīn Muhammad Balkhi, also known as Rumi and is ref ...
(spiritual guide of Rumi
Jalāl al-Dīn Muḥammad Rūmī ( fa, جلالالدین محمد رومی), also known as Jalāl al-Dīn Muḥammad Balkhī (), Mevlânâ/Mawlānā ( fa, مولانا, lit= our master) and Mevlevî/Mawlawī ( fa, مولوی, lit= my ma ...
), Najm al-Din Daya who described Omar Khayyam as "an unhappy philosopher, atheist, and materialist", and Attar
Attar or Attoor ( ar, عطار, ) may refer to:
People
*Attar (name)
*Fariduddin Attar, 12th-century Persian poet
Places
*Attar (Madhya Pradesh), the location of Attar railway station, Madhya Pradesh, India
*Attar, Iran, a village in Razavi Kho ...
who regarded him not as a fellow-mystic but a free-thinking scientist who awaited punishments hereafter.
Seyyed Hossein Nasr
Seyyed Hossein Nasr (; fa, سید حسین نصر, born April 7, 1933) is an Iranian philosopher and University Professor of Islamic studies at George Washington University.
Born in Tehran, Nasr completed his education in Iran and the United St ...
argues that it is "reductive" to use a literal interpretation of his verses (many of which are of uncertain authenticity to begin with) to establish Omar Khayyam's philosophy. Instead, he adduces Khayyam's interpretive translation of Avicenna
Ibn Sina ( fa, ابن سینا; 980 – June 1037 CE), commonly known in the West as Avicenna (), was a Persian polymath who is regarded as one of the most significant physicians, astronomers, philosophers, and writers of the Islamic G ...
's treatise ''Discourse on Unity'' (), where he expresses orthodox views on Divine Unity in agreement with the author. S. H. Nasr, 2006, Islamic Philosophy from Its Origin to the Present, Chapter 9., pp. 165–183 The prose works believed to be Omar's are written in the Peripatetic
Peripatetic may refer to:
*Peripatetic school, a school of philosophy in Ancient Greece
*Peripatetic axiom
* Peripatetic minority, a mobile population moving among settled populations offering a craft or trade.
*Peripatetic Jats
There are several ...
style and are explicitly theistic, dealing with subjects such as the existence of God
The existence of God (or more generally, the existence of deities) is a subject of debate in theology, philosophy of religion and popular culture. A wide variety of arguments for and against the existence of God or deities can be categorized ...
and theodicy
Theodicy () means vindication of God. It is to answer the question of why a good God permits the manifestation of evil, thus resolving the issue of the problem of evil. Some theodicies also address the problem of evil "to make the existence of ...
. As noted by Bowen these works indicate his involvement in the problems of metaphysics rather than in the subtleties of Sufism. As evidence of Khayyam's faith and/or conformity to Islamic customs, Aminrazavi mentions that in his treatises he offers salutations and prayers, praising God and Muhammad
Muhammad ( ar, مُحَمَّد; 570 – 8 June 632 Common Era, CE) was an Arab religious, social, and political leader and the founder of Islam. According to Muhammad in Islam, Islamic doctrine, he was a prophet Divine inspiration, di ...
. In most biographical extracts, he is referred to with religious honorifics such as , ''The Patron of Faith'' (), and ''The Evidence of Truth'' (). He also notes that biographers who praise his religiosity generally avoid making reference to his poetry, while the ones who mention his poetry often do not praise his religious character. For instance, Al-Bayhaqi's account, which antedates by some years other biographical notices, speaks of Omar as a very pious man who professed orthodox views down to his last hour.Meyerhof, M. (1948). 'Alī al-Bayhaqī's Tatimmat Siwān al-Hikma: A Biographical Work on Learned Men of the Islam. Osiris, 8, 122–217.
On the basis of all the existing textual and biographical evidence, the question remains somewhat open, and as a result Khayyam has received sharply conflicting appreciations and criticisms.
Reception
The various biographical extracts referring to Omar Khayyam describe him as unequalled in scientific knowledge and achievement during his time. Many called him by the epithet ''King of the Wise'' ( ar, ملك الحکماء).Shahrazuri
Shams al-Din Muhammad ibn Mahmud Shahrazuri was a 13th-century Muslim physician, historian and philosopher. He was of Kurdish origin. It appears that he was alive in AD 1288. However, it is also said that he died in the same year.
Shahrazuri was ...
(d. 1300) esteems him highly as a mathematician, and claims that he may be regarded as "the successor of Avicenna in the various branches of philosophic learning". Al-Qifti
'Alī ibn Yūsuf al-Qifṭī or Ali Ibn Yusuf the Qifti (of Qift, his home city) (), he was ''Jamāl al-Dīn Abū al-Ḥasan 'Alī ibn Yūsuf ibn Ibrāhīm ibn 'Abd al-Wahid al-Shaybānī'' () (ca. 1172–1248); an Egyptian Arab historian, biog ...
(d. 1248), even though disagreeing with his views, concedes he was "unrivalled in his knowledge of natural philosophy and astronomy". Despite being hailed as a poet by a number of biographers, according to Richard N. Frye
Richard Nelson Frye (January 10, 1920 – March 27, 2014) was an American scholar of Iranian and Central Asian studies, and Aga Khan Professor Emeritus of Iranian Studies at Harvard University. His professional areas of interest were Irania ...
"it is still possible to argue that Khayyam's status as a poet of the first rank is a comparatively late development."
Thomas Hyde
Thomas Hyde (29 June 163618 February 1703) was an English linguist, historian, librarian, classicist, and orientalist. His chief work was the 1700 'On the Ancient Religion of the Persians'' the first attempt to use Arab and Persian sources ...
was the first European to call attention to Omar and to translate one of his quatrains into Latin (''Historia religionis veterum Persarum eorumque magorum'', 1700). Western interest in Persia grew with the Orientalism
In art history, literature and cultural studies, Orientalism is the imitation or depiction of aspects in the Eastern world. These depictions are usually done by writers, designers, and artists from the Western world. In particular, Orientalist p ...
movement in the 19th century. Joseph von Hammer-Purgstall
Joseph Freiherr von Hammer-Purgstall (9 June 1774 – 23 November 1856) was an Austrian orientalist and historian. He is considered one of the most accomplished Orientalists of his time. He was critical of the trend of ascribing classical or a ...
(1774–1856) translated some of Khayyam's poems into German in 1818, and Gore Ouseley
Sir Gore Ouseley, 1st Baronet GCH, PC (24 June 1770 – 18 November 1844), was a British entrepreneur, linguist and diplomat. He was born in 1770 and died at Hall Barn Park, Beaconsfield, Buckinghamshire in 1844. He negotiated an important t ...
(1770–1844) into English in 1846, but Khayyam remained relatively unknown in the West until after the publication of Edward FitzGerald's ''Rubaiyat of Omar Khayyam
''Rubáiyát of Omar Khayyám'' is the title that Edward FitzGerald gave to his 1859 translation from Persian to English of a selection of quatrains (') attributed to Omar Khayyam (1048–1131), dubbed "the Astronomer-Poet of Persia".
Altho ...
'' in 1859. FitzGerald's work at first was unsuccessful but was popularised by Whitley Stokes
Whitley Stokes, CSI, CIE, FBA (28 February 1830 – 13 April 1909) was an Irish lawyer and Celtic scholar.
Background
He was a son of William Stokes (1804–1878), and a grandson of Whitley Stokes the physician and anti-Malthusian (1763� ...
from 1861 onward, and the work came to be greatly admired by the Pre-Raphaelites
The Pre-Raphaelite Brotherhood (later known as the Pre-Raphaelites) was a group of English painters, poets, and art critics, founded in 1848 by William Holman Hunt, John Everett Millais, Dante Gabriel Rossetti, William Michael Rossetti, James ...
. In 1872 FitzGerald had a third edition printed which increased interest in the work in America. By the 1880s, the book was extremely well known throughout the English-speaking world, to the extent of the formation of numerous "Omar Khayyam Clubs" and a "fin de siècle cult of the Rubaiyat". Khayyam's poems have been translated into many languages; many of the more recent ones are more literal than that of FitzGerald.''The Great Umar Khayyam: A Global Reception of the Rubaiyat'' (AUP – Leiden University Press) by A. A. Seyed-Gohrab, 2012.
FitzGerald's translation was a factor in rekindling interest in Khayyam as a poet even in his native Iran.Simidchieva, M. (2011). FitzGerald's Rubáiyát and Agnosticism. In A. Poole, C. Van Ruymbeke, & W. Martin (Eds.), FitzGerald's Rubáiyát of Omar Khayyám: Popularity and Neglect (pp. 55–72). Anthem Press. Sadegh Hedayat
Sadegh Hedayat ( fa, صادق هدایت ; 17 February 1903 – 9 April 1951) was an Iranian writer and translator. Best known for his novel '' The Blind Owl'', he was one of the earliest Iranian writers to adopt literary modernism in their care ...
in his ''Songs of Khayyam'' (''Taranehha-ye Khayyam'', 1934) reintroduced Omar's poetic legacy to modern Iran. Under the Pahlavi dynasty
The Pahlavi dynasty ( fa, دودمان پهلوی) was the last Iranian royal dynasty, ruling for almost 54 years between 1925 and 1979. The dynasty was founded by Reza Shah Pahlavi, a non-aristocratic Mazanderani soldier in modern times, who ...
, a new monument
A monument is a type of structure that was explicitly created to commemorate a person or event, or which has become relevant to a social group as a part of their remembrance of historic times or cultural heritage, due to its artistic, his ...
of white marble, designed by the architect Houshang Seyhoun
Houshang Seyhoun, ( fa, هوشنگ سیحون) (August 22, 1920 – May 26, 2014) was an Iranian architect, sculptor, painter, scholar and professor. He studied fine arts at the École nationale supérieure des Beaux-Arts in Paris, and earned a deg ...
, was erected over his tomb. A statue by Abolhassan Sadighi
Abolhassan Sadighi ( fa, ابوالحسن صدیقی) (5 October 1894 – 11 December 1995) was an Iranian sculptor and painter and was known as Master Sadighi. He was a student of Kamal-ol-molk, Ghaffari.
The statue of Ferdowsi in the Ferdowsi ...
was erected in Laleh Park
Laleh Park (Pârk-e Laleh, formerly called Park-e Farah after Farah Diba), is a large recreation area of the Iranian capital Tehran. ''Laleh'' (لاله) is the Persian word for tulip, which is also a popular symbol in Iranian culture.
The park ...
, Tehran
Tehran (; fa, تهران ) is the largest city in Tehran Province and the capital of Iran. With a population of around 9 million in the city and around 16 million in the larger metropolitan area of Greater Tehran, Tehran is the most popul ...
in the 1960s, and a bust by the same sculptor was placed near Khayyam's mausoleum in Nishapur. In 2009, the state of Iran donated a pavilion
In architecture, ''pavilion'' has several meanings:
* It may be a subsidiary building that is either positioned separately or as an attachment to a main building. Often it is associated with pleasure. In palaces and traditional mansions of Asia ...
to the United Nations Office in Vienna
The United Nations Office at Vienna (UNOV) is one of the four major office sites of the United Nations where numerous different UN agencies have a joint presence. The office complex is located in Vienna, the capital of Austria, and is part of the ...
, inaugurated at Vienna International Center
The Vienna International Centre (VIC) is the campus and building complex hosting the United Nations Office at Vienna (UNOV; in de-AT, Büro der Vereinten Nationen in Wien). It is colloquially also known as UNO City.
Overview
The VIC, designed ...
. In 2016, three statues of Khayyam were unveiled: one at the University of Oklahoma
The University of Oklahoma (OU) is a Public university, public research university in Norman, Oklahoma. Founded in 1890, it had existed in Oklahoma Territory near Indian Territory for 17 years before the two Territories became the state of Oklahom ...
, one in Nishapur and one in Florence, Italy. Over 150 composer
A composer is a person who writes music. The term is especially used to indicate composers of Western classical music, or those who are composers by occupation. Many composers are, or were, also skilled performers of music.
Etymology and Defi ...
s have used the ''Rubaiyat'' as their source of inspiration. The earliest such composer was Liza Lehmann.
FitzGerald rendered Omar's name as "Tentmaker", and the anglicized name of "Omar the Tentmaker" resonated in English-speaking popular culture for a while. Thus, Nathan Haskell Dole published a novel called ''Omar, the Tentmaker: A Romance of Old Persia'' in 1898. ''Omar the Tentmaker of Nishapur, Naishapur'' is a historical novel by John Smith Clarke, published in 1910. "Omar the Tentmaker" is also the title of a 1914 play by Richard Walton Tully in an oriental setting, adapted as a Omar the Tentmaker (film), silent film in 1922. US General Omar Bradley was given the nickname "Omar the Tent-Maker" in World War II.
The Moving Finger quatrain
 The quatrain by Omar Khayyam known as "The Moving Finger", in the form of its translation by the English poet Edward FitzGerald (poet), Edward Fitzgerald is one of the most popular quatrains in the Anglosphere. It reads:
The title of the novel "The Moving Finger" written by Agatha Christie and published in 1942 was inspired by this quatrain of the translation of ''
The quatrain by Omar Khayyam known as "The Moving Finger", in the form of its translation by the English poet Edward FitzGerald (poet), Edward Fitzgerald is one of the most popular quatrains in the Anglosphere. It reads:
The title of the novel "The Moving Finger" written by Agatha Christie and published in 1942 was inspired by this quatrain of the translation of ''Rubaiyat of Omar Khayyam
''Rubáiyát of Omar Khayyám'' is the title that Edward FitzGerald gave to his 1859 translation from Persian to English of a selection of quatrains (') attributed to Omar Khayyam (1048–1131), dubbed "the Astronomer-Poet of Persia".
Altho ...
'' by Edward FitzGerald (poet), Edward Fitzgerald. Martin Luther King Jr., Martin Luther King also cites this quatrain of Omar Khayyam in one of his speeches "Beyond Vietnam: A Time to Break Silence":
In one of his apologetic speeches about the Clinton–Lewinsky scandal, Bill Clinton, the 42nd president of the US, also cites this quatrain.
Other popular culture references
The French-Lebanese writer Amin Maalouf based the first half of his historical fiction novel ''Samarkand (novel), Samarkand'' on Khayyam's life and the creation of his Rubaiyat. The sculptor Eduardo Chillida produced four massive iron pieces titled ''Mesa de Omar Khayyam'' (Omar Khayyam's Table) in the 1980s. The lunar crater Omar Khayyam (crater), Omar Khayyam was named in his honour in 1970, as was the minor planet 3095 Omarkhayyam discovered by Soviet Union, Soviet astronomer Lyudmila Zhuravlyova in 1980. Google has released two Google Doodles commemorating him. The first was on his 964th birthday on 18 May 2012. The second was on his 971st birthday on 18 May 2019.Gallery
Rubaiyat of Omar Khayyam
''Rubáiyát of Omar Khayyám'' is the title that Edward FitzGerald gave to his 1859 translation from Persian to English of a selection of quatrains (') attributed to Omar Khayyam (1048–1131), dubbed "the Astronomer-Poet of Persia".
Altho ...
'' by Adelaide Hanscom Leeson (c. 1905).
File:At the Tomb of Omar Khayyam - by Jay Hambidge.jpg, "At the Tomb of Omar Khayyam" by Jay Hambidge (1911).
File:Persian Scholar pavilion in Viena UN (Omar Khayyam).jpg, The statue of Khayyam in United Nations Office in Vienna
The United Nations Office at Vienna (UNOV) is one of the four major office sites of the United Nations where numerous different UN agencies have a joint presence. The office complex is located in Vienna, the capital of Austria, and is part of the ...
as a part of Persian Scholars Pavilion donated by Iran.
File:Hakim Omar Khayam - panoramio.jpg, A statue of Omar Khayyam in Laleh Park
Laleh Park (Pârk-e Laleh, formerly called Park-e Farah after Farah Diba), is a large recreation area of the Iranian capital Tehran. ''Laleh'' (لاله) is the Persian word for tulip, which is also a popular symbol in Iranian culture.
The park ...
of Tehran
Tehran (; fa, تهران ) is the largest city in Tehran Province and the capital of Iran. With a population of around 9 million in the city and around 16 million in the larger metropolitan area of Greater Tehran, Tehran is the most popul ...
. Made by Abolhassan Sadighi
Abolhassan Sadighi ( fa, ابوالحسن صدیقی) (5 October 1894 – 11 December 1995) was an Iranian sculptor and painter and was known as Master Sadighi. He was a student of Kamal-ol-molk, Ghaffari.
The statue of Ferdowsi in the Ferdowsi ...
.
File:Bucureşti - Omar Khayam 3.jpg, Statue of Omar Khayyam in Bucharest
File:آرامگاه خیام نیشابور Mausoleum of Omar Khayyam.jpg, alt=Mausoleum of Omar Khayyam in Neyshabur, Iran. Some of his rubáiyáts are used as calligraphic (taliq script) decoration on the exterior body of his mausoleum., Mausoleum of Omar Khayyam in Nishapur
Nishapur or officially Romanized as Neyshabur ( fa, ;Or also "نیشاپور" which is closer to its original and historic meaning though it is less commonly used by modern native Persian speakers. In Persian poetry, the name of this city is wr ...
, Iran. Some of his rubáiyáts are used as Taliq script, calligraphic (taliq script) decoration on the exterior body of his mausoleum.
File:Madrid - Ciudad Universitaria, Monumento a Omar Jayyam 1.jpg, Monument to Omar Khayyam in Ciudad Universitaria of Madrid
See also
* ''The Keeper: The Legend of Omar Khayyam'' * ''Nozhat al-Majales'' * Omar Khayyam (film), ''Omar Khayyam'' (film) * Noted Khayyamologists: ** Badiozzaman Forouzanfar ** Abdolhossein ZarrinkoobReferences
Notes
Citations
Further reading
* * * * Browne, E. (1899). "Yet More Light on 'Umar-i-Khayyām". ''Journal of the Royal Asiatic Society of Great Britain and Ireland'', 409–420. . * * * * Ross, E. (1927). "Omar Khayyam". ''Bulletin of the School of Oriental Studies'', University of London, 4(3), 433–439. . * * Rypka, Jan (1968). ''History of Iranian Literature''. Reidel Publishing Company. . * *External links
* * *PDF version
Umar Khayyam
in the ''Stanford Encyclopedia of Philosophy''
The illustrated Rubáiyát of Omar Khayyám
at Internet Archive. {{DEFAULTSORT:Khayyam, Omar Omar Khayyam, 1048 births 1131 deaths 11th-century Iranian astronomers 11th-century Persian-language poets 12th-century astronomers 12th-century Persian-language writers 12th-century Iranian mathematicians 12th-century Persian-language poets Algebra Mathematicians from Nishapur 12th-century Iranian astronomers 11th-century Persian-language writers Iranian philosophers Persian physicists Persian spiritual writers Philosophers from Nishapur Scholars from the Seljuk Empire Poets from the Seljuk Empire