Oblique asymptote

In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related contexts, an asymptote of a curve is a line which is tangent to the curve at a point at infinity.

The word asymptote is derived from the Greek ἀσύμπτωτος (''asumptōtos'') which means "not falling together", from ἀ priv. + σύν "together" + πτωτ-ός "fallen". The term was introduced by Apollonius of Perga in his work on conic sections, but in contrast to its modern meaning, he used it to mean any line that does not intersect the given curve.

There are three kinds of asymptotes: ''horizontal'', ''vertical'' and ''oblique''. For curves given by the graph of a function , horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to Vertical asymptotes are vertical lines near which the function grows without bound. An oblique asymptote has a slope that is non-zero but finite, such that the graph of the function approaches it as ''x'' tends to

More generally, one curve is a ''curvilinear asymptote'' of another (as opposed to a ''linear asymptote'') if the distance between the two curves tends to zero as they tend to infinity, although the term ''asymptote'' by itself is usually reserved for linear asymptotes.

Asymptotes convey information about the behavior of curves ''in the large'', and determining the asymptotes of a function is an important step in sketching its graph. The study of asymptotes of functions, construed in a broad sense, forms a part of the subject of asymptotic analysis.

Introduction

The idea that a curve may come arbitrarily close to a line without actually becoming the same may seem to counter everyday experience. The representations of a line and a curve as marks on a piece of paper or as pixels on a computer screen have a positive width. So if they were to be extended far enough they would seem to merge, at least as far as the eye could discern. But these are physical representations of the corresponding mathematical entities; the line and the curve are idealized concepts whose width is 0 (see Line). Therefore, the understanding of the idea of an asymptote requires an effort of reason rather than experience.

Consider the graph of the function $f(x) = \frac$ shown in this section. The coordinates of the points on the curve are of the form $\left(x, \frac\right)$ where x is a number other than 0. For example, the graph contains the points (1, 1), (2, 0.5), (5, 0.2), (10, 0.1), ... As the values of $x$ become larger and larger, say 100, 1,000, 10,000 ..., putting them far to the right of the illustration, the corresponding values of $y$, .01, .001, .0001, ..., become infinitesimal relative to the scale shown. But no matter how large $x$ becomes, its reciprocal $\frac$ is never 0, so the curve never actually touches the ''x''-axis. Similarly, as the values of $x$ become smaller and smaller, say .01, .001, .0001, ..., making them infinitesimal relative to the scale shown, the corresponding values of $y$, 100, 1,000, 10,000 ..., become larger and larger. So the curve extends farther and farther upward as it comes closer and closer to the ''y''-axis. Thus, both the ''x'' and ''y''-axis are asymptotes of the curve. These ideas are part of the basis of concept of a limit in mathematics, and this connection is explained more fully below.

Asymptotes of functions

The asymptotes most commonly encountered in the study of calculus are of curves of the form . These can be computed using limits and classified into ''horizontal'', ''vertical'' and ''oblique'' asymptotes depending on their orientation. Horizontal asymptotes are horizontal lines that the graph of the function approaches as ''x'' tends to +∞ or −∞. As the name indicates they are parallel to the ''x''-axis. Vertical asymptotes are vertical lines (perpendicular to the ''x''-axis) near which the function grows without bound. Oblique asymptotes are diagonal lines such that the difference between the curve and the line approaches 0 as ''x'' tends to +∞ or −∞.

Vertical asymptotes

The line ''x'' = ''a'' is a ''vertical asymptote'' of the graph of the function if at least one of the following statements is true:

# $\lim_ f(x)=\pm\infty,$
# $\lim_ f(x)=\pm\infty,$

where $\lim_$ is the limit as ''x'' approaches the value ''a'' from the left (from lesser values), and $\lim_$ is the limit as ''x'' approaches ''a'' from the right.

For example, if ƒ(''x'') = ''x''/(''x''–1), the numerator approaches 1 and the denominator approaches 0 as ''x'' approaches 1. So
:$\lim_\frac=+\infty$
:$\lim_\frac=-\infty$
and the curve has a vertical asymptote ''x'' = 1.

The function ''ƒ''(''x'') may or may not be defined at ''a'', and its precise value at the point ''x'' = ''a'' does not affect the asymptote. For example, for the function

:$f(x) = \begin \frac & \text x > 0, \\ 5 & \text x \le 0. \end$

has a limit of +∞ as , ''ƒ''(''x'') has the vertical asymptote , even though ''ƒ''(0) = 5. The graph of this function does intersect the vertical asymptote once, at (0, 5). It is impossible for the graph of a function to intersect a vertical asymptote (or a vertical line in general) in more than one point. Moreover, if a function is continuous at each point where it is defined, it is impossible that its graph does intersect any vertical asymptote.

A common example of a vertical asymptote is the case of a rational function at a point x such that the denominator is zero and the numerator is non-zero.

If a function has a vertical asymptote, then it isn't necessarily true that the derivative of the function has a vertical asymptote at the same place. An example is
:$f(x) = \tfrac 1x + \sin(\tfrac 1x)\quad$ at $\quad x=0$.

This function has a vertical asymptote at $x=0,$ because
:$\lim_ f(x) = \lim_\left(\tfrac 1x + \sin\left(\tfrac 1x\right)\right) = +\infty,$

and

:$\lim_ f(x) = \lim_\left(\tfrac 1x + \sin\left(\tfrac 1x\right)\right) = -\infty$.

The derivative of $f$ is the function
:$f'(x)=\frac$.

For the sequence of points
:$x_n=\frac,\quad$ for $\quad n=0,1,2,\ldots$

that approaches $x=0$ both from the left and from the right, the values $f'(x_n)$ are constantly $0$. Therefore, both one-sided limits of $f'$ at $0$ can be neither $+\infty$ nor $-\infty$. Hence $f'(x)$ doesn't have a vertical asymptote at $x=0$.

Horizontal asymptotes

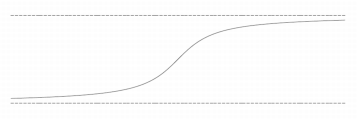
''Horizontal asymptotes'' are horizontal lines that the graph of the function approaches as . The horizontal line ''y'' = ''c'' is a horizontal asymptote of the function ''y'' = ''ƒ''(''x'') if
:$\lim_f(x)=c$ or $\lim_f(x)=c$.
In the first case, ''ƒ''(''x'') has ''y'' = ''c'' as asymptote when ''x'' tends to , and in the second ''ƒ''(''x'') has ''y'' = ''c'' as an asymptote as ''x'' tends to .

For example, the arctangent function satisfies
:$\lim_\arctan(x)=-\frac$ and $\lim_\arctan(x)=\frac.$

So the line is a horizontal asymptote for the arctangent when ''x'' tends to , and is a horizontal asymptote for the arctangent when ''x'' tends to .

Functions may lack horizontal asymptotes on either or both sides, or may have one horizontal asymptote that is the same in both directions. For example, the function has a horizontal asymptote at ''y'' = 0 when ''x'' tends both to and because, respectively,
:$\lim_\frac=\lim_\frac=0.$

Other common functions that have one or two horizontal asymptotes include (that has an hyperbola as it graph), the Gaussian function $x\mapsto \exp(-x^2),$ the error function, and the logistic function.

Oblique asymptotes

When a linear asymptote is not parallel to the ''x''- or ''y''-axis, it is called an ''oblique asymptote'' or ''slant asymptote''. A function ''ƒ''(''x'') is asymptotic to the straight line (''m'' ≠ 0) if

:\lim_\left f(x)-(mx+n)\right= 0 \, \mbox \lim_\left f(x)-(mx+n)\right= 0.

In the first case the line is an oblique asymptote of ''ƒ''(''x'') when ''x'' tends to +∞, and in the second case the line is an oblique asymptote of ''ƒ''(''x'') when ''x'' tends to −∞.

An example is ''ƒ''(''x'') = ''x'' + 1/''x'', which has the oblique asymptote ''y'' = ''x'' (that is ''m'' = 1, ''n'' = 0) as seen in the limits
:\lim_\left (x)-x\right/math>
:=\lim_\left left(x+\frac\right)-x\right/math>
:$=\lim_\frac=0.$

Elementary methods for identifying asymptotes

The asymptotes of many elementary functions can be found without the explicit use of limits (although the derivations of such methods typically use limits).

General computation of oblique asymptotes for functions

The oblique asymptote, for the function ''f''(''x''), will be given by the equation ''y'' = ''mx'' + ''n''. The value for ''m'' is computed first and is given by

:$m\;\stackrel\,\lim_f(x)/x$

where ''a'' is either $-\infty$ or $+\infty$ depending on the case being studied. It is good practice to treat the two cases separately. If this limit doesn't exist then there is no oblique asymptote in that direction.

Having ''m'' then the value for ''n'' can be computed by

:$n\;\stackrel\,\lim_(f(x)-mx)$

where ''a'' should be the same value used before. If this limit fails to exist then there is no oblique asymptote in that direction, even should the limit defining ''m'' exist. Otherwise is the oblique asymptote of ''ƒ''(''x'') as ''x'' tends to ''a''.

For example, the function has

:$m=\lim_f(x)/x=\lim_\frac=2$ and then
:$n=\lim_(f(x)-mx)=\lim_\left(\frac-2x\right)=3$

so that is the asymptote of ''ƒ''(''x'') when ''x'' tends to +∞.

The function has

:$m=\lim_f(x)/x=\lim_\frac=0$ and then

:$n=\lim_(f(x)-mx)=\lim_\ln x$, which does not exist.

So does not have an asymptote when ''x'' tends to +∞.

Asymptotes for rational functions

A rational function has at most one horizontal asymptote or oblique (slant) asymptote, and possibly many vertical asymptotes.

The degree of the numerator and degree of the denominator determine whether or not there are any horizontal or oblique asymptotes. The cases are tabulated below, where deg(numerator) is the degree of the numerator, and deg(denominator) is the degree of the denominator.

The vertical asymptotes occur only when the denominator is zero (If both the numerator and denominator are zero, the multiplicities of the zero are compared). For example, the following function has vertical asymptotes at ''x'' = 0, and ''x'' = 1, but not at ''x'' = 2.
:$f(x)=\frac=\frac$

Oblique asymptotes of rational functions

When the numerator of a rational function has degree exactly one greater than the denominator, the function has an oblique (slant) asymptote. The asymptote is the polynomial term after dividing the numerator and denominator. This phenomenon occurs because when dividing the fraction, there will be a linear term, and a remainder. For example, consider the function
:$f(x)=\frac=x+\frac$
shown to the right. As the value of ''x'' increases, ''f'' approaches the asymptote ''y'' = ''x''. This is because the other term, 1/(''x''+1), approaches 0.

If the degree of the numerator is more than 1 larger than the degree of the denominator, and the denominator does not divide the numerator, there will be a nonzero remainder that goes to zero as ''x'' increases, but the quotient will not be linear, and the function does not have an oblique asymptote.

Transformations of known functions

If a known function has an asymptote (such as ''y''=0 for ''f''(x)=''e''^''x''), then the translations of it also have an asymptote.
* If ''x''=''a'' is a vertical asymptote of ''f''(''x''), then ''x''=''a''+''h'' is a vertical asymptote of ''f''(''x''-''h'')
* If ''y''=''c'' is a horizontal asymptote of ''f''(''x''), then ''y''=''c''+''k'' is a horizontal asymptote of ''f''(''x'')+''k''

If a known function has an asymptote, then the scaling of the function also have an asymptote.

* If ''y''=''ax''+''b'' is an asymptote of ''f''(''x''), then ''y''=''cax''+''cb'' is an asymptote of ''cf''(''x'')
For example, ''f''(''x'')=''e''^''x''-1+2 has horizontal asymptote ''y''=0+2=2, and no vertical or oblique asymptotes.

General definition

Let be a parametric plane curve, in coordinates ''A''(''t'') = (''x''(''t''),''y''(''t'')). Suppose that the curve tends to infinity, that is:
:$\lim_(x^2(t)+y^2(t))=\infty.$
A line ℓ is an asymptote of ''A'' if the distance from the point ''A''(''t'') to ℓ tends to zero as ''t'' → ''b''. From the definition, only open curves that have some infinite branch can have an asymptote. No closed curve can have an asymptote.

For example, the upper right branch of the curve ''y'' = 1/''x'' can be defined parametrically as ''x'' = ''t'', ''y'' = 1/''t'' (where ''t'' > 0). First, ''x'' → ∞ as ''t'' → ∞ and the distance from the curve to the ''x''-axis is 1/''t'' which approaches 0 as ''t'' → ∞. Therefore, the ''x''-axis is an asymptote of the curve. Also, ''y'' → ∞ as ''t'' → 0 from the right, and the distance between the curve and the ''y''-axis is ''t'' which approaches 0 as ''t'' → 0. So the ''y''-axis is also an asymptote. A similar argument shows that the lower left branch of the curve also has the same two lines as asymptotes.

Although the definition here uses a parameterization of the curve, the notion of asymptote does not depend on the parameterization. In fact, if the equation of the line is $ax+by+c=0$ then the distance from the point ''A''(''t'') = (''x''(''t''),''y''(''t'')) to the line is given by
:$\frac$
if γ(''t'') is a change of parameterization then the distance becomes
:$\frac$
which tends to zero simultaneously as the previous expression.

An important case is when the curve is the graph of a real function (a function of one real variable and returning real values). The graph of the function ''y'' = ''ƒ''(''x'') is the set of points of the plane with coordinates (''x'',''ƒ''(''x'')). For this, a parameterization is
:$t\mapsto (t,f(t)).$
This parameterization is to be considered over the open intervals (''a'',''b''), where ''a'' can be −∞ and ''b'' can be +∞.

An asymptote can be either vertical or non-vertical (oblique or horizontal). In the first case its equation is ''x'' = ''c'', for some real number ''c''. The non-vertical case has equation , where ''m'' and $n$ are real numbers. All three types of asymptotes can be present at the same time in specific examples. Unlike asymptotes for curves that are graphs of functions, a general curve may have more than two non-vertical asymptotes, and may cross its vertical asymptotes more than once.

Curvilinear asymptotes

Let be a parametric plane curve, in coordinates ''A''(''t'') = (''x''(''t''),''y''(''t'')), and ''B'' be another (unparameterized) curve. Suppose, as before, that the curve ''A'' tends to infinity. The curve ''B'' is a curvilinear asymptote of ''A'' if the shortest distance from the point ''A''(''t'') to a point on ''B'' tends to zero as ''t'' → ''b''. Sometimes ''B'' is simply referred to as an asymptote of ''A'', when there is no risk of confusion with linear asymptotes.

For example, the function
:$y = \frac$
has a curvilinear asymptote , which is known as a ''parabolic asymptote'' because it is a parabola rather than a straight line.

Asymptotes and curve sketching

Asymptotes are used in procedures of curve sketching. An asymptote serves as a guide line to show the behavior of the curve towards infinity. In order to get better approximations of the curve, curvilinear asymptotes have also been used although the term asymptotic curve seems to be preferred.

Algebraic curves

The asymptotes of an algebraic curve in the affine plane are the lines that are tangent to the projectivized curve through a point at infinity. For example, one may identify the asymptotes to the unit hyperbola in this manner. Asymptotes are often considered only for real curves, although they also make sense when defined in this way for curves over an arbitrary field.

A plane curve of degree ''n'' intersects its asymptote at most at ''n''−2 other points, by Bézout's theorem, as the intersection at infinity is of multiplicity at least two. For a conic, there are a pair of lines that do not intersect the conic at any complex point: these are the two asymptotes of the conic.

A plane algebraic curve is defined by an equation of the form ''P''(''x'',''y'') = 0 where ''P'' is a polynomial of degree ''n''
:$P(x,y) = P_n(x,y) + P_(x,y) + \cdots + P_1(x,y) + P_0$
where ''P''_''k'' is homogeneous of degree ''k''. Vanishing of the linear factors of the highest degree term ''P''_''n'' defines the asymptotes of the curve: setting , if , then the line
:$Q'_x(b,a)x+Q'_y(b,a)y + P_(b,a)=0$
is an asymptote if $Q'_x(b,a)$ and $Q'_y(b,a)$ are not both zero. If $Q'_x(b,a)=Q'_y(b,a)=0$ and $P_(b,a)\neq 0$, there is no asymptote, but the curve has a branch that looks like a branch of parabola. Such a branch is called a , even when it does not have any parabola that is a curvilinear asymptote. If $Q'_x(b,a)=Q'_y(b,a)=P_(b,a)=0,$ the curve has a singular point at infinity which may have several asymptotes or parabolic branches.

Over the complex numbers, ''P''_''n'' splits into linear factors, each of which defines an asymptote (or several for multiple factors). Over the reals, ''P''_''n'' splits in factors that are linear or quadratic factors. Only the linear factors correspond to infinite (real) branches of the curve, but if a linear factor has multiplicity greater than one, the curve may have several asymptotes or parabolic branches. It may also occur that such a multiple linear factor corresponds to two complex conjugate branches, and does not corresponds to any infinite branch of the real curve. For example, the curve has no real points outside the square $, x, \leq 1, , y, \leq 1$, but its highest order term gives the linear factor ''x'' with multiplicity 4, leading to the unique asymptote ''x''=0.

Asymptotic cone

The hyperbola
:$\frac-\frac= 1$
has the two asymptotes
:$y=\pm\fracx.$
The equation for the union of these two lines is
:$\frac-\frac=0.$
Similarly, the hyperboloid
:$\frac-\frac-\frac=1$
is said to have the asymptotic coneP. Frost ''Solid geometry'' (1875)
This has a more general treatment of asymptotic surfaces.

:$\frac-\frac-\frac=0.$

The distance between the hyperboloid and cone approaches 0 as the distance from the origin approaches infinity.

More generally, consider a surface that has an implicit equation
$P_d(x,y,z)+P_(x,y,z) + \cdots P_0=0,$
where the $P_i$ are homogeneous polynomials of degree $i$ and $P_=0$. Then the equation $P_d(x,y,z)=0$ defines a cone which is centered at the origin. It is called an asymptotic cone, because the distance to the cone of a point of the surface tends to zero when the point on the surface tends to infinity.

See also

* Big O notation

References

; General references
*

; Specific references

External links

*

Hyperboloid and Asymptotic Cone, string surface model, 1872
from the Science Museum

{{Authority control

Mathematical analysis
Analytic geometry