Numerical modeling (geology) on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 A general numerical model study usually consists of the following components:
# Mathematical model is a simplified description of the geological problem, such as equations and boundary conditions. These governing equations of the model are often
A general numerical model study usually consists of the following components:
# Mathematical model is a simplified description of the geological problem, such as equations and boundary conditions. These governing equations of the model are often
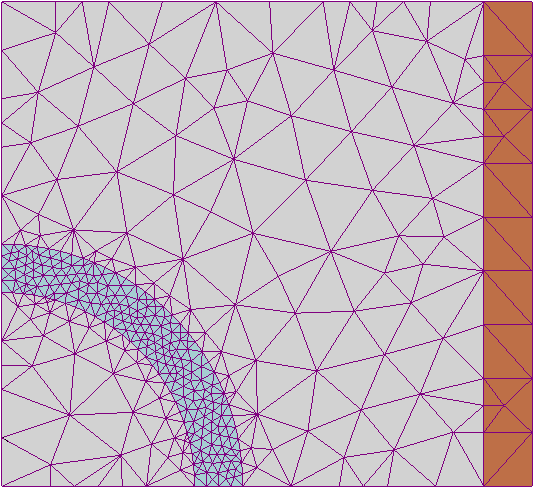 Numerical methods are techniques to approximate the governing equations in the mathematical models.
Common numerical methods include
Numerical methods are techniques to approximate the governing equations in the mathematical models.
Common numerical methods include
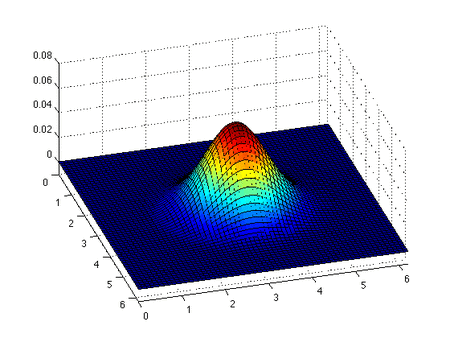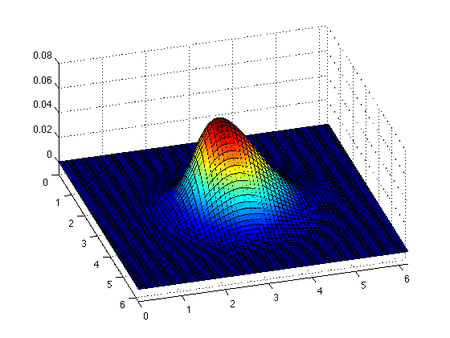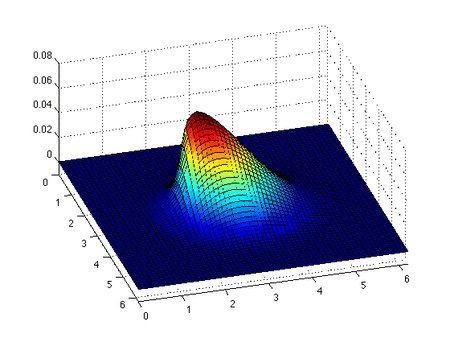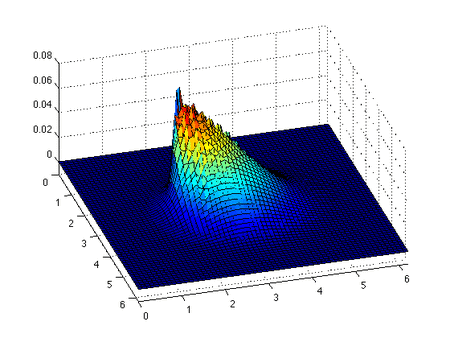
 Consider a function with single-valued derivatives that are continuous and finite functions of , according to
Consider a function with single-valued derivatives that are continuous and finite functions of , according to
 In
In geology
Geology (). is a branch of natural science concerned with the Earth and other astronomical objects, the rocks of which they are composed, and the processes by which they change over time. Modern geology significantly overlaps all other Earth ...
, numerical modeling is a widely applied technique to tackle complex geological problems by computational simulation of geological scenarios.
Numerical modeling uses mathematical model
A mathematical model is an abstract and concrete, abstract description of a concrete system using mathematics, mathematical concepts and language of mathematics, language. The process of developing a mathematical model is termed ''mathematical m ...
s to describe the physical conditions of geological scenarios using numbers and equations. Nevertheless, some of their equations are difficult to solve directly, such as partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s. With numerical models, geologists can use methods, such as finite difference method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial doma ...
s, to approximate the solutions of these equations. Numerical experiments can then be performed in these models, yielding the results that can be interpreted in the context of geological process. Both qualitative and quantitative understanding of a variety of geological processes can be developed via these experiments.
Numerical modelling has been used to assist in the study of rock mechanics
Rock mechanics is a theoretical and applied science of the mechanical behavior of rocks and rock masses.
Compared to geology, it is the branch of mechanics concerned with the response of rock and rock masses to the force fields of their physical ...
, thermal history of rocks, movements of tectonic plates and the Earth's mantle. Flow of fluids is simulated using numerical methods, and this shows how groundwater
Groundwater is the water present beneath Earth's surface in rock and Pore space in soil, soil pore spaces and in the fractures of stratum, rock formations. About 30 percent of all readily available fresh water in the world is groundwater. A unit ...
moves, or how motions of the molten outer core yields the geomagnetic field.
History
Prior to the development of numerical modeling, analog modeling, which simulates nature with reduced scales in mass, length, and time, was one of the major ways to tackle geological problems, for instance, to model the formation of thrust belts. Simple analytic or semi-analytic mathematical models were also used to deal with relatively simple geological problems quantitatively. In the late 1960s to 1970s, following the development of finite-element methods in solvingcontinuum mechanics
Continuum mechanics is a branch of mechanics that deals with the deformation of and transmission of forces through materials modeled as a ''continuous medium'' (also called a ''continuum'') rather than as discrete particles.
Continuum mec ...
problems for civil engineering
Civil engineering is a regulation and licensure in engineering, professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including public works such as roads ...
, numerical methods were adapted for modeling complex geological phenomena, for example, folding and mantle convection
Mantle convection is the very slow creep of Earth's solid silicate mantle as convection currents carry heat from the interior to the planet's surface. Mantle convection causes tectonic plates to move around the Earth's surface.
The Earth's l ...
. With advances in computer technology, the accuracy of numerical models has been improved. Numerical modeling has become an important tool for tackling geological problems, especially for the parts of the Earth that are difficult to observe directly, such as the mantle and core
Core or cores may refer to:
Science and technology
* Core (anatomy), everything except the appendages
* Core (laboratory), a highly specialized shared research resource
* Core (manufacturing), used in casting and molding
* Core (optical fiber ...
. Yet analog modeling is still useful in modeling geological scenarios that are difficult to capture in numerical models, and the combination of analog and numerical modeling can be useful to improve understanding of the Earth's processes.
Components
partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s that are difficult to solve directly since it involves the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
of the function, for example, the wave equation
The wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields such as mechanical waves (e.g. water waves, sound waves and seismic waves) or electromagnetic waves (including light ...
.
# Discretization methods and numerical methods convert those governing equations in the mathematical models to discrete equations. These discrete equations can approximate the solution of the governing equations. Common methods include the finite element
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat tran ...
, finite difference
A finite difference is a mathematical expression of the form . Finite differences (or the associated difference quotients) are often used as approximations of derivatives, such as in numerical differentiation.
The difference operator, commonly d ...
, or finite volume method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations.
In the finite volume method, volume integrals in a partial differential equation that contain a divergen ...
that subdivide the object of interest into smaller pieces (element) by mesh. These discrete equations can then be solved in each element numerically. The discrete element method uses another approach, this method reassembling the object of interest from numerous tiny particles. Simple governing equations are then applied to the interactions between particles.
# Algorithms are computer programs that compute the solution using the idea of the above numerical methods.
# Interpretations are made from the solutions given by the numerical models.
Properties
A good numerical model usually has some of the following properties: * Consistent: Numerical models often divide the object into smaller elements. If the model is consistent, the result of the numerical model is nearly the same as what the mathematical model predicts when the element size is nearly zero. In other words, the error between the discrete equations used in the numerical model and the governing equations in the mathematical model tends to zero when the space of the mesh (size of element) becomes close to zero. *Stable
A stable is a building in which working animals are kept, especially horses or oxen. The building is usually divided into stalls, and may include storage for equipment and feed.
Styles
There are many different types of stables in use tod ...
: In a stable numerical model, the error during the computation of the numerical methods does not amplify. The error of an unstable model will stack up quickly and lead to an incorrect result. A ''stable'' and ''consistent'' numerical model has the same output as the exact solution in the mathematical model when the spacing of the mesh (size of element) is extremely small.
* Converging: The output of the numerical model is closer to the actual solution of the governing equations in the mathematical models when the spacing of mesh (size of element) reduces, which is usually checked by carrying out numerical experiments.
* Conserved: The physical quantities in the models, such as mass and momentum, are conserved. Since the equations in the mathematical models are usually derived from various conservation laws, the model result should not violate these premises.
* Bounded: The solution given by the numerical model has reasonable physical bounds with respect to the mathematical models, for instance mass and volume should be positive.
* Accurate: The solution given by the numerical models is close to the real solution predicted by the mathematical model.
Computation
The following are some key aspects of ideas in developing numerical models in geology. First, the way to describe the object and motion should be decided (kinematic
In physics, kinematics studies the geometrical aspects of motion of physical objects independent of forces that set them in motion. Constrained motion such as linked machine parts are also described as kinematics.
Kinematics is concerned with s ...
description). Then, governing equations that describe the geological problems are written, for example, the heat equation
In mathematics and physics (more specifically thermodynamics), the heat equation is a parabolic partial differential equation. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quanti ...
s describe the flow of heat in a system. Since some of these equations cannot be solved directly, numerical methods are used to approximate the solution of the governing equations.
Kinematic descriptions
In numerical models and mathematical models, there are two different approaches to describe the motion of matter: Eulerian and Lagrangian. In geology, both approaches are commonly used to model fluid flow like mantle convection, where an Eulerian grid is used for computation and Lagrangian markers are used to visualize the motion. Recently, there have been models that try to describe different parts using different approaches to combine the advantages of these two approaches. This combined approach is called the arbitrary Lagrangian-Eulerian approach.Eulerian
The Eulerian approach considers the changes of the physical quantities, such as mass and velocity, of a ''fixed location'' with time. It is similar to looking at how river water flows past a bridge. Mathematically, the physical quantities can be expressed as a function of location and time. This approach is useful for fluid and homogeneous (uniform) materials that have no natural boundary.Lagrangian
The Lagrangian approach, on the other hand, considers the change of physical quantities, such as the volume, of ''fixed elements'' of matter over time. It is similar to looking at a certain collection of water molecules as they flow downstream in a river. Using the Lagrangian approach, it is easier to follow solid objects which have natural boundary to separate them from the surrounding.Governing equations
Following are some basic equations that are commonly used to describe physical phenomena, for example, how the matter in a geologic system moves or flows and how heat energy is distributed in a system. These equations are usually the core of the mathematical model.Continuity equation
Thecontinuity equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity ...
is a mathematical version of stating that the geologic object or medium is continuous, which means no empty space can be found in the object. This equation is commonly used in numerical modeling in geology.
One example is the continuity equation of mass of fluid. Based on the law of ''conservation of mass'', for a fluid with density at position in a fixed volume of fluid, the rate of change of mass is equal to the outward fluid flow across the boundary :
where is the volume element and is the velocity at .
In Lagrangian form:
In Eulerian form:
This equation is useful when the model involves continuous fluid flow, like the mantle is over geological time scales.
Momentum equation
The momentum equation describes how matter moves in response to force applied. It is an expression ofNewton's second law of motion
Newton's laws of motion are three physical laws that describe the relationship between the motion of an object and the forces acting on it. These laws, which provide the basis for Newtonian mechanics, can be paraphrased as follows:
# A body re ...
.
Consider a fixed volume of matter. By the law of ''conservation of momentum'', the rate of change of volume is equal to:
* external force applied on the element
* plus normal stress and shear stress applied on the surface bounding the element
* minus the momentum moving out of the element on that surface
where is the volume element, is the velocity.
After simplifications and integrations, for any volume , the Eulerian form of this equation is:
Heat equation
The heat equations describe how heat energy flows in a system. From the law of conservation of energy, the rate of change of energy of a fixed volume of mass is equal to: * work done at the boundary * plus work done by external force in the volume * minus heatconduction
Conductor or conduction may refer to:
Biology and medicine
* Bone conduction, the conduction of sound to the inner ear
* Conduction aphasia, a language disorder
Mathematics
* Conductor (ring theory)
* Conductor of an abelian variety
* Condu ...
across boundary
* minus heat convection
Convection is single or Multiphase flow, multiphase fluid flow that occurs Spontaneous process, spontaneously through the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoy ...
across boundary
* plus heat produced internally
Mathematically:
where is the volume element, is the velocity, is the temperature, is the conduction coefficient and is the rate of heat production.
Numerical methods
 Numerical methods are techniques to approximate the governing equations in the mathematical models.
Common numerical methods include
Numerical methods are techniques to approximate the governing equations in the mathematical models.
Common numerical methods include finite element method
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat tran ...
, spectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The idea is to write the solution of the differential equation as a sum of certain " basis funct ...
, finite difference method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial doma ...
, and finite volume method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations.
In the finite volume method, volume integrals in a partial differential equation that contain a divergen ...
. These methods are used to approximate the solution of governing differential equations in the mathematical model by dissecting the domain into meshes or grids and applying simpler equations to individual elements or nodes in the mesh.
The discrete element method uses another approach. The object is considered an assemblage of small particles.
Finite element method
Thefinite element method
Finite element method (FEM) is a popular method for numerically solving differential equations arising in engineering and mathematical modeling. Typical problem areas of interest include the traditional fields of structural analysis, heat tran ...
subdivides the object (or domain) into smaller, non-overlapping elements (or subdomains) and these elements are connected at the nodes. The solution for the partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s are then approximated by simpler element equations, usually polynomial
In mathematics, a polynomial is a Expression (mathematics), mathematical expression consisting of indeterminate (variable), indeterminates (also called variable (mathematics), variables) and coefficients, that involves only the operations of addit ...
s. Then these element equations are combined into equations for the entire object, i.e. the contribution of each element is summed up to model the response of the whole object. This method is commonly used to solve mechanical problems. The following are the general steps of using the finite element method:
# Select the element type and subdivide the object. Common element types include triangular, quadrilateral, tetrahedral, etc. Different types of elements should be chosen for different problems.
# Decide the function of displacement. The function of displacement governs how the elements move. Linear, quadratic, or cubic polynomial
In mathematics, a cubic function is a function (mathematics), function of the form f(x)=ax^3+bx^2+cx+d, that is, a polynomial function of degree three. In many texts, the ''coefficients'' , , , and are supposed to be real numbers, and the func ...
functions are commonly used.
# Decide the displacement-strain relation. The displacement of the element changes or deforms the element's shape in what is technically called strain. This relation calculates how much strain the element experienced due to the displacement.
# Decide the strain-stress relation. The deformation of the element induces stress to the element, which is the force
In physics, a force is an influence that can cause an Physical object, object to change its velocity unless counterbalanced by other forces. In mechanics, force makes ideas like 'pushing' or 'pulling' mathematically precise. Because the Magnitu ...
applied to the element. This relation calculates the amount of stress experienced by the element due to the strain. One of the examples of this relation is Hooke's law
In physics, Hooke's law is an empirical law which states that the force () needed to extend or compress a spring by some distance () scales linearly with respect to that distance—that is, where is a constant factor characteristic of ...
.
# Derive equations of stiffness and stiffness matrix for elements. The stress also causes the element to deform; the stiffness
Stiffness is the extent to which an object resists deformation in response to an applied force.
The complementary concept is flexibility or pliability: the more flexible an object is, the less stiff it is.
Calculations
The stiffness, k, of a ...
(the rigidity) of the elements indicates how much it will deform in response to the stress. The stiffness of the elements in different directions is represented in matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
form for simpler operation during calculation.
# Combine the element equations into global equations. The contributions of every element are summed up to a set of equations that describe the whole system.
# Apply boundary conditions. The predefined conditions at the boundary, such as temperature, stress, and other physical quantities are introduced to the boundary of the system.
# Solve for displacement. As time evolves, the displacement of the elements are solved step by step.
# Solve for strains and stress. After the displacement is calculated, the strains and stress are computed using the relations in steps 3 and 4.

Spectral method
Thespectral method
Spectral methods are a class of techniques used in applied mathematics and scientific computing to numerically solve certain differential equations. The idea is to write the solution of the differential equation as a sum of certain " basis funct ...
is similar to the finite element method. The major difference is that spectral method uses basis functions, possibly by using a fast Fourier transformation (FFT) that approximates the function by the sum of numerous simple functions. These kinds of basis functions can then be applied to the whole domain and approximate the governing partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s. Therefore, each calculation takes the information from the whole domain into account while the finite element method only takes the information from the neighborhood. As a result, the spectral method converges exponentially and is suitable for solving problems involving a high variability in time or space.
Finite volume method
Thefinite volume method
The finite volume method (FVM) is a method for representing and evaluating partial differential equations in the form of algebraic equations.
In the finite volume method, volume integrals in a partial differential equation that contain a divergen ...
is also similar to the finite element method. It also subdivides the object of interest into smaller volumes (or elements), then the physical quantities are solved over the control volume as fluxes of these quantities across the different faces. The equations used are usually based on the conservation or balance of physical quantities, like mass and energy.
The finite volume method can be applied on irregular meshes like the finite element method. The element equations are still physically meaningful. However, it is difficult to get better accuracy, as the higher order version of element equations are not well-defined.
Finite difference method
Thefinite difference method
In numerical analysis, finite-difference methods (FDM) are a class of numerical techniques for solving differential equations by approximating Derivative, derivatives with Finite difference approximation, finite differences. Both the spatial doma ...
approximates differential equations by approximating the derivative
In mathematics, the derivative is a fundamental tool that quantifies the sensitivity to change of a function's output with respect to its input. The derivative of a function of a single variable at a chosen input value, when it exists, is t ...
with a difference equation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
, which is the major method to solve partial differential equation
In mathematics, a partial differential equation (PDE) is an equation which involves a multivariable function and one or more of its partial derivatives.
The function is often thought of as an "unknown" that solves the equation, similar to ho ...
s.
Taylor's theorem
In calculus, Taylor's theorem gives an approximation of a k-times differentiable function around a given point by a polynomial of degree k, called the k-th-order Taylor polynomial. For a smooth function, the Taylor polynomial is the truncation a ...
:
and
Summing up the above expressions:
Ignore the terms with higher than 4th power of , then: