Negami's Conjecture on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 The graph of the
The graph of the  The graph of a ''k''-gonal
The graph of a ''k''-gonal
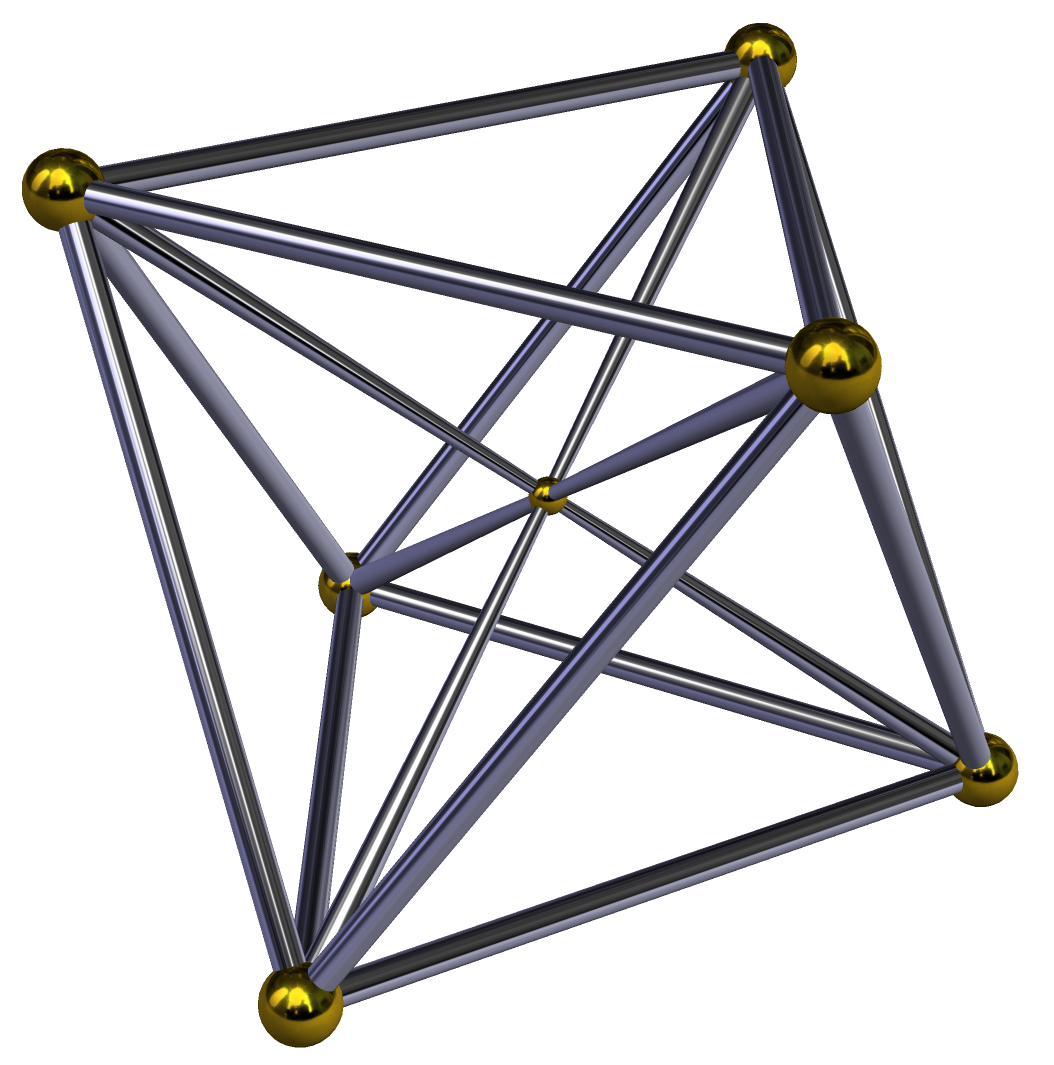 Like the graphs with planar covers, the graphs with projective plane embeddings can be characterized by forbidden minors. In this case the exact set of forbidden minors is known: there are 35 of them. 32 of these are connected, and one of these 32 graphs necessarily appears as a minor in any connected non-projective-planar graph. Since Negami made his conjecture, it has been proven that 31 of these 32 forbidden minors either do not have planar covers, or can be reduced by Y-Δ transforms to a simpler graph on this list. The one remaining graph for which this has not yet been done is ''K''1,2,2,2, a seven-vertex
Like the graphs with planar covers, the graphs with projective plane embeddings can be characterized by forbidden minors. In this case the exact set of forbidden minors is known: there are 35 of them. 32 of these are connected, and one of these 32 graphs necessarily appears as a minor in any connected non-projective-planar graph. Since Negami made his conjecture, it has been proven that 31 of these 32 forbidden minors either do not have planar covers, or can be reduced by Y-Δ transforms to a simpler graph on this list. The one remaining graph for which this has not yet been done is ''K''1,2,2,2, a seven-vertex
graph theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conn ...
, a planar cover of a finite graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
''G'' is a finite covering graph
In the mathematical discipline of graph theory, a graph is a covering graph of another graph if there is a covering map from the vertex set of to the vertex set of . A covering map is a surjection and a local isomorphism: the neighbourhood of ...
of ''G'' that is itself a planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cro ...
. Every graph that can be embedded
Embedded or embedding (alternatively imbedded or imbedding) may refer to:
Science
* Embedding, in mathematics, one instance of some mathematical object contained within another instance
** Graph embedding
* Embedded generation, a distributed ge ...
into the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that ...
has a planar cover; an unsolved conjecture of Seiya Negami states that these are the only graphs with planar covers., p. 1
The existence of a planar cover is a minor-closed graph property,, Proposition 1, p. 2 and so can be characterized by finitely many forbidden minors
In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden ...
, but the exact set of forbidden minors is not known. For the same reason, there exists a polynomial time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by ...
algorithm for testing whether a given graph has a planar cover, but an explicit description of this algorithm is not known.
Definition
A ''covering map'' from one graph ''C'' to another graph ''H'' may be described by a function ''f'' from the vertices of ''C'' onto the vertices of ''H'' that, for each vertex ''v'' of ''C'', gives a bijection between the neighbors of ''v'' and the neighbors of ''f''(''v''). If ''H'' is aconnected graph
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgra ...
, each vertex of ''H'' must have the same number of pre-images in ''C''; this number is called the ''ply'' of the map, and ''C'' is called a covering graph
In the mathematical discipline of graph theory, a graph is a covering graph of another graph if there is a covering map from the vertex set of to the vertex set of . A covering map is a surjection and a local isomorphism: the neighbourhood of ...
of ''G''. If ''C'' and ''H'' are both finite, and ''C'' is a planar graph
In graph theory, a planar graph is a graph that can be embedded in the plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. In other words, it can be drawn in such a way that no edges cro ...
, then ''C'' is called a planar cover of ''H''.
Examples
 The graph of the
The graph of the dodecahedron
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentag ...
has a symmetry that maps each vertex to the antipodal vertex. The set of antipodal pairs of vertices and their adjacencies can itself be viewed as a graph, the Petersen graph
In the mathematics, mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertex (graph theory), vertices and 15 edge (graph theory), edges. It is a small graph that serves as a useful example and counterexample for ...
. The dodecahedron forms a planar cover of this nonplanar graph. As this example shows, not every graph with a planar cover is itself planar. However, when a planar graph covers a non-planar one, the ply must be an even number
In mathematics, parity is the property of an integer of whether it is even or odd. An integer is even if it is a multiple of two, and odd if it is not.. For example, −4, 0, 82 are even because
\begin
-2 \cdot 2 &= -4 \\
0 \cdot 2 &= 0 \\
4 ...
.
 The graph of a ''k''-gonal
The graph of a ''k''-gonal prism
Prism usually refers to:
* Prism (optics), a transparent optical component with flat surfaces that refract light
* Prism (geometry), a kind of polyhedron
Prism may also refer to:
Science and mathematics
* Prism (geology), a type of sedimentary ...
has 2''k'' vertices, and is planar with two ''k''-gon faces and ''k'' quadrilateral faces. If ''k'' = ''ab'', with ''a'' ≥ 2 and ''b'' ≥ 3, then it has an ''a''-ply covering map to a ''b''-fonal prism, in which two vertices of the ''k''-prism are mapped to the same vertex of the ''b''-prism if they both belong to the same ''k''-gonal face and the distance from one to the other is a multiple of ''b''. For instance, the dodecagonal prism
In geometry, the dodecagonal prism is the tenth in an infinite set of prisms, formed by square sides and two regular dodecagon caps.
If faces are all regular, it is a uniform polyhedron.
Use
It is used in the construction of two prismatic u ...
can form a 2-ply cover of the hexagonal prism
In geometry, the hexagonal prism is a prism with hexagonal base. Prisms are polyhedrons; this polyhedron has 8 faces, 18 edges, and 12 vertices..
Since it has 8 faces, it is an octahedron. However, the term ''octahedron'' is primarily used t ...
, a 3-ply cover of the cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross.
The cube is the on ...
, or a 4-ply cover of the triangular prism
In geometry, a triangular prism is a three-sided prism; it is a polyhedron made of a triangular base, a translated copy, and 3 faces joining corresponding sides. A right triangular prism has rectangular sides, otherwise it is ''oblique''. ...
. These examples show that a graph may have many different planar covers, and may be the planar cover for many other graphs. Additionally they show that the ply of a planar cover may be arbitrarily large.
They are not the only covers involving prisms: for instance, the hexagonal prism can also cover a non-planar graph, the utility graph
As a topic of economics, utility is used to model worth or value. Its usage has evolved significantly over time. The term was introduced initially as a measure of pleasure or happiness as part of the theory of utilitarianism by moral philosophe ...
''K''3,3, by identifying antipodal pairs of vertices.
Cover-preserving operations
If a graph ''H'' has a planar cover, so does everygraph minor
In graph theory, an undirected graph is called a minor of the graph if can be formed from by deleting edges and vertices and by contracting edges.
The theory of graph minors began with Wagner's theorem that a graph is planar if and only i ...
of ''H''. A minor ''G'' of ''H'' may be formed by deleting edges and vertices from ''H'', and by contracting edges of ''H''. The covering graph ''C'' can be transformed in the same way: for each deleted edge or vertex in ''H'', delete its preimage in ''C'', and for each contracted edge or vertex in ''H'', contract its preimage in ''C''. The result of applying these operations to ''C'' is a minor of ''C'' that covers ''G''. Since every minor of a planar graph is itself planar, this gives a planar cover of the minor ''G''.
Because the graphs with planar covers are closed under the operation of taking minors, it follows from the Robertson–Seymour theorem
In graph theory, the Robertson–Seymour theorem (also called the graph minor theorem) states that the undirected graphs, partially ordered by the graph minor relationship, form a well-quasi-ordering. Equivalently, every family of graphs that i ...
that they may be characterized by a finite set of forbidden minors
In graph theory, a branch of mathematics, many important families of graphs can be described by a finite set of individual graphs that do not belong to the family and further exclude all graphs from the family which contain any of these forbidden ...
. A graph is a forbidden minor for this property if it has no planar cover, but all of its minors do have planar covers. This characterization can be used to prove the existence of a polynomial time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by ...
algorithm that tests for the existence of a planar cover, by searching for each of the forbidden minors and returning that a planar cover exists only if this search fails to find any of them. However, because the exact set of forbidden minors for this property is not known, this proof of existence is non-constructive
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object by creating or providing a method for creating the object. This is in contrast to a non-constructive proof (also known as an existen ...
, and does not lead to an explicit description of the set of forbidden minors or of the algorithm based on them.
Another graph operation
In the mathematical field of graph theory, graph operations are operations which produce new graphs from initial ones. They include both unary (one input) and binary (two input) operations.
Unary operations
Unary operations create a new graph ...
that preserves the existence of a planar cover is the Y-Δ transform
The Y-Δ transform, also written wye-delta and also known by many other names, is a mathematical technique to simplify the analysis of an electrical network. The name derives from the shapes of the circuit diagrams, which look respectively like th ...
, which replaces any degree-three vertex of a graph ''H'' by a triangle connecting its three neighbors. However, the reverse of this transformation, a Δ-Y transform, does not necessarily preserve planar covers.
Additionally, a disjoint union
In mathematics, a disjoint union (or discriminated union) of a family of sets (A_i : i\in I) is a set A, often denoted by \bigsqcup_ A_i, with an injection of each A_i into A, such that the images of these injections form a partition of A ...
of two graphs that have covers will also have a cover, formed as the disjoint union of the covering graphs. If the two covers have the same ply as each other, then this will also be the ply of their union.
Negami's conjecture
If a graph ''H'' has anembedding
In mathematics, an embedding (or imbedding) is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup.
When some object X is said to be embedded in another object Y, the embedding is giv ...
into the projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines (namely, parallel lines) that ...
, then it necessarily has a planar cover, given by the preimage of ''H'' in the orientable double cover
In mathematics, orientability is a property of some topological spaces such as real vector spaces, Euclidean spaces, surfaces, and more generally manifolds that allows a consistent definition of "clockwise" and "counterclockwise". A space is ...
of the projective plane, which is a sphere.
proved, conversely, that if a connected graph
In mathematics and computer science, connectivity is one of the basic concepts of graph theory: it asks for the minimum number of elements (nodes or edges) that need to be removed to separate the remaining nodes into two or more isolated subgra ...
''H'' has a two-ply planar cover then ''H'' must have an embedding into the projective plane. The assumption that ''H'' is connected is necessary here, because a disjoint union of projective-planar graphs may not itself be projective-planar but will still have a planar cover, the disjoint union of the orientable double covers.
A ''regular cover'' of a graph ''H'' is one that comes from a group of symmetries of its covering graph: the preimages of each vertex in ''H'' are an orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such a ...
of the group. proved that every connected graph with a planar regular cover can be embedded into the projective plane. Based on these two results, he conjectured that in fact every connected graph with a planar cover is projective.
As of 2013, this conjecture remains unsolved. It is also known as Negami's "1-2-∞ conjecture", because it can be reformulated as stating that the minimum ply of a planar cover, if it exists, must be either 1 or 2.
 Like the graphs with planar covers, the graphs with projective plane embeddings can be characterized by forbidden minors. In this case the exact set of forbidden minors is known: there are 35 of them. 32 of these are connected, and one of these 32 graphs necessarily appears as a minor in any connected non-projective-planar graph. Since Negami made his conjecture, it has been proven that 31 of these 32 forbidden minors either do not have planar covers, or can be reduced by Y-Δ transforms to a simpler graph on this list. The one remaining graph for which this has not yet been done is ''K''1,2,2,2, a seven-vertex
Like the graphs with planar covers, the graphs with projective plane embeddings can be characterized by forbidden minors. In this case the exact set of forbidden minors is known: there are 35 of them. 32 of these are connected, and one of these 32 graphs necessarily appears as a minor in any connected non-projective-planar graph. Since Negami made his conjecture, it has been proven that 31 of these 32 forbidden minors either do not have planar covers, or can be reduced by Y-Δ transforms to a simpler graph on this list. The one remaining graph for which this has not yet been done is ''K''1,2,2,2, a seven-vertex apex graph
In graph theory, a branch of mathematics, an apex graph is a graph that can be made planar by the removal of a single vertex. The deleted vertex is called an apex of the graph. It is ''an'' apex, not ''the'' apex because an apex graph may have m ...
that forms the skeleton of a four-dimensional octahedral pyramid
In 4-dimensional geometry, the octahedral pyramid is bounded by one octahedron on the base and 8 triangular pyramid cells which meet at the apex. Since an octahedron has a circumradius divided by edge length less than one, the triangular pyramids ...
. If ''K''1,2,2,2 could be shown not to have any planar covers, this would complete a proof of the conjecture. On the other hand, if the conjecture is false, ''K''1,2,2,2 would necessarily be its smallest counterexample.
A related conjecture by Michael Fellows
Michael Ralph Fellows AC HFRSNZ MAE (born June 15, 1952 in Upland, California) is a computer scientist and the Elite Professor of Computer Science in the Department of Informatics at the University of Bergen, Norway as of January 2016.
Biograph ...
, now solved, concerns planar ''emulators'', a generalization of planar covers that maps graph neighborhoods surjectively rather than bijectively. The graphs with planar emulators, like those with planar covers, are closed under minors and Y-Δ transforms. In 1988, independently of Negami, Fellows conjectured that the graphs with planar emulators are exactly the graphs that can be embedded into the projective plane. The conjecture is true for ''regular'' emulators, coming from automomorphisms of the underlying covering graph, by a result analogous to the result of for regular planar covers.
However, several of the 32 connected forbidden minors for projective-planar graphs turn out to have planar emulators. Therefore, Fellows' conjecture is false. Finding a full set of forbidden minors for the existence of planar emulators remains an open problem., p. 10
Notes
References
Secondary sources about Negami's conjecture
*. Page numbers in notes refer to the preprint version. *.Primary sources about planar covers
*. *. *. *. *. *. *. *. *. *.Supporting literature
* *. *. *. *. *. *. *. {{refend Graph theory objects Graph minor theory