Multi-criteria Decision-making on:
[Wikipedia]
[Google]
[Amazon]
A Brief History prepared by Steuer and Zionts
*Malakooti, B. (2013). Operations and Production Systems with Multiple Objectives. John Wiley & Sons. {{DEFAULTSORT:Multi-Criteria Decision Analysis Decision analysis Management systems Mathematical optimization Utility sr:Вишекритеријумска оптимизација
Multiple-criteria decision-making (MCDM) or multiple-criteria decision analysis (MCDA) is a sub-discipline of
 :
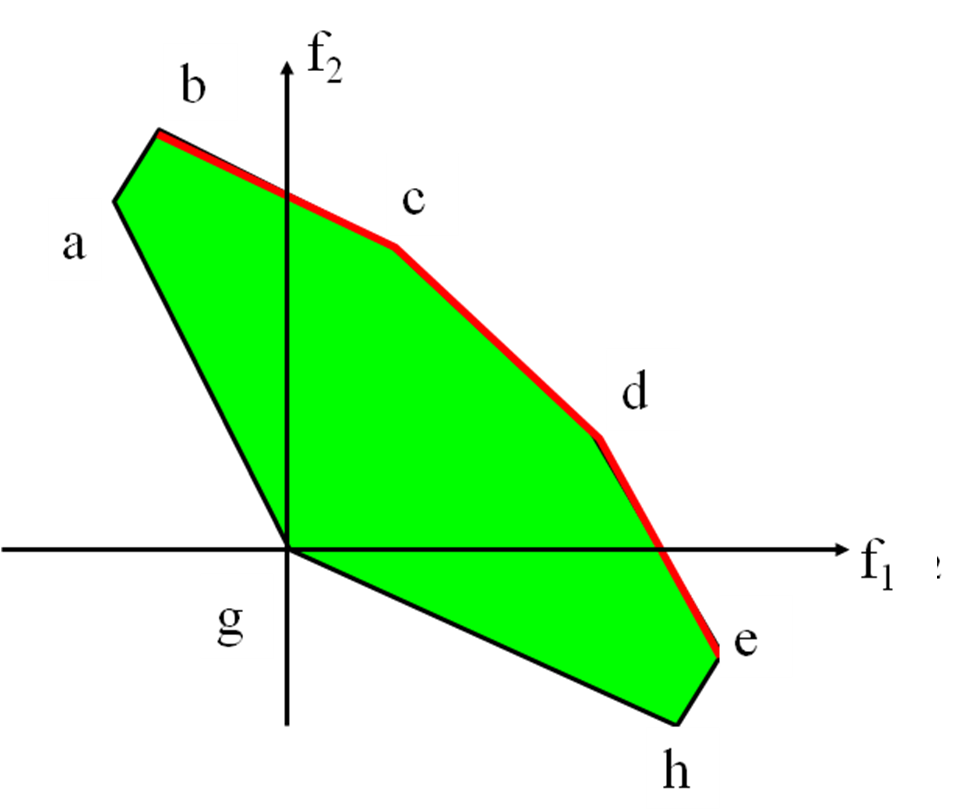
In Figure 1, the extreme points "e" and "b" maximize the first and second objectives, respectively. The red boundary between those two extreme points represents the efficient set. It can be seen from the figure that, for any feasible solution outside the efficient set, it is possible to improve both objectives by some points on the efficient set. Conversely, for any point on the efficient set, it is not possible to improve both objectives by moving to any other feasible solution. At these solutions, one has to sacrifice from one of the objectives in order to improve the other objective.
Due to its simplicity, the above problem can be represented in criterion space by replacing the with the as follows:
:
In Figure 1, the extreme points "e" and "b" maximize the first and second objectives, respectively. The red boundary between those two extreme points represents the efficient set. It can be seen from the figure that, for any feasible solution outside the efficient set, it is possible to improve both objectives by some points on the efficient set. Conversely, for any point on the efficient set, it is not possible to improve both objectives by moving to any other feasible solution. At these solutions, one has to sacrifice from one of the objectives in order to improve the other objective.
Due to its simplicity, the above problem can be represented in criterion space by replacing the with the as follows:
 ::
::
:: subject to
:::
:::
:::
:::
:::
:::
:::
We present the criterion space graphically in Figure 2. It is easier to detect the nondominated points (corresponding to efficient solutions in the decision space) in the criterion space. The north-east region of the feasible space constitutes the set of nondominated points (for maximization problems).
::
::
:: subject to
:::
:::
:::
:::
:::
:::
:::
We present the criterion space graphically in Figure 2. It is easier to detect the nondominated points (corresponding to efficient solutions in the decision space) in the criterion space. The north-east region of the feasible space constitutes the set of nondominated points (for maximization problems).
 Achievement scalarizing functions also combine multiple criteria into a single criterion by weighting them in a very special way. They create rectangular contours going away from a reference point towards the available efficient solutions. This special structure empower achievement scalarizing functions to reach any efficient solution. This is a powerful property that makes these functions very useful for MCDM problems.
Mathematically, we can represent the corresponding problem as
:: = ,
::subject to
:::
The achievement scalarizing function can be used to project any point (feasible or infeasible) on the efficient frontier. Any point (supported or not) can be reached. The second term in the objective function is required to avoid generating inefficient solutions. Figure 3 demonstrates how a feasible point, , and an infeasible point, , are projected onto the nondominated points, and , respectively, along the direction using an achievement scalarizing function. The dashed and solid contours correspond to the objective function contours with and without the second term of the objective function, respectively.
Achievement scalarizing functions also combine multiple criteria into a single criterion by weighting them in a very special way. They create rectangular contours going away from a reference point towards the available efficient solutions. This special structure empower achievement scalarizing functions to reach any efficient solution. This is a powerful property that makes these functions very useful for MCDM problems.
Mathematically, we can represent the corresponding problem as
:: = ,
::subject to
:::
The achievement scalarizing function can be used to project any point (feasible or infeasible) on the efficient frontier. Any point (supported or not) can be reached. The second term in the objective function is required to avoid generating inefficient solutions. Figure 3 demonstrates how a feasible point, , and an infeasible point, , are projected onto the nondominated points, and , respectively, along the direction using an achievement scalarizing function. The dashed and solid contours correspond to the objective function contours with and without the second term of the objective function, respectively.
(Outranking)
* operations research
Operations research ( en-GB, operational research) (U.S. Air Force Specialty Code: Operations Analysis), often shortened to the initialism OR, is a discipline that deals with the development and application of analytical methods to improve dec ...
that explicitly evaluates multiple conflicting criteria
Criterion, or its plural form criteria, may refer to:
General
* Criterion, Oregon, a historic unincorporated community in the United States
* Criterion Place, a proposed skyscraper in West Yorkshire, England
* Criterion Restaurant, in London, En ...
in decision making
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either ra ...
(both in daily life and in settings such as business, government and medicine). Conflicting criteria are typical in evaluating options: cost
In Production (economics), production, research, retail, and accounting, a cost is the value of money that has been used up to produce something or deliver a service, and hence is not available for use anymore. In business, the cost may be one o ...
or price is usually one of the main criteria, and some measure of quality is typically another criterion, easily in conflict with the cost. In purchasing a car, cost, comfort, safety, and fuel economy may be some of the main criteria we consider – it is unusual that the cheapest car is the most comfortable and the safest one. In portfolio management, managers are interested in getting high returns while simultaneously reducing risks; however, the stocks that have the potential of bringing high returns typically carry high risk of losing money. In a service industry, customer satisfaction and the cost of providing service are fundamental conflicting criteria.
In their daily lives, people usually weigh multiple criteria implicitly and may be comfortable with the consequences of such decisions that are made based on only intuition
Intuition is the ability to acquire knowledge without recourse to conscious reasoning. Different fields use the word "intuition" in very different ways, including but not limited to: direct access to unconscious knowledge; unconscious cognition; ...
. On the other hand, when stakes are high, it is important to properly structure the problem and explicitly evaluate multiple criteria. In making the decision of whether to build a nuclear power plant or not, and where to build it, there are not only very complex issues involving multiple criteria, but there are also multiple parties who are deeply affected by the consequences.
Structuring complex problems well and considering multiple criteria explicitly leads to more informed and better decisions. There have been important advances in this field since the start of the modern multiple-criteria decision-making discipline in the early 1960s. A variety of approaches and methods, many implemented by specialized decision-making software Decision-making software (DM software) is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
An early example of DM so ...
,Weistroffer, HR, and Li, Y (2016). "Multiple criteria decision analysis software". Ch 29 in: Greco, S, Ehrgott, M and Figueira, J, eds, ''Multiple Criteria Decision Analysis: State of the Art Surveys Series'', Springer: New York. have been developed for their application in an array of disciplines, ranging from politics and business to the environment and energy.
Foundations, concepts, definitions
MCDM or MCDA are well-known acronyms for ''multiple-criteria decision-making'' and ''multiple-criteria decision analysis''; Stanley Zionts helped popularizing the acronym with his 1979 article "MCDM – If not a Roman Numeral, then What?", intended for an entrepreneurial audience. MCDM is concerned with structuring and solving decision and planning problems involving multiple criteria. The purpose is to support decision-makers facing such problems. Typically, there does not exist a unique optimal solution for such problems and it is necessary to use decision-makers' preferences to differentiate between solutions. "Solving" can be interpreted in different ways. It could correspond to choosing the "best" alternative from a set of available alternatives (where "best" can be interpreted as "the most preferred alternative" of a decision-maker). Another interpretation of "solving" could be choosing a small set of good alternatives, or grouping alternatives into different preference sets. An extreme interpretation could be to find all "efficient" or " nondominated" alternatives (which we will define shortly). The difficulty of the problem originates from the presence of more than one criterion. There is no longer a unique optimal solution to an MCDM problem that can be obtained without incorporating preference information. The concept of an optimal solution is often replaced by the set of nondominated solutions. A solution is called nondominated if it is not possible to improve it in any criterion without sacrificing it in another. Therefore, it makes sense for the decision-maker to choose a solution from the nondominated set. Otherwise, she/he could do better in terms of some or all of the criteria, and not do worse in any of them. Generally, however, the set of nondominated solutions is too large to be presented to the decision-maker for the final choice. Hence we need tools that help the decision-maker focus on the preferred solutions (or alternatives). Normally one has to "tradeoff" certain criteria for others. MCDM has been an active area of research since the 1970s. There are several MCDM-related organizations including the International Society on Multi-criteria Decision Making, Euro Working Group on MCDA, and INFORMS Section on MCDM. For a history see: Köksalan, Wallenius and Zionts (2011). MCDM draws upon knowledge in many fields including: * Mathematics *Decision analysis Decision analysis (DA) is the discipline comprising the philosophy, methodology, and professional practice necessary to address important decisions in a formal manner. Decision analysis includes many procedures, methods, and tools for identifying, ...
* Economics
Economics () is the social science that studies the production, distribution, and consumption of goods and services.
Economics focuses on the behaviour and interactions of economic agents and how economies work. Microeconomics analy ...
* Computer technology
Computing is any goal-oriented activity requiring, benefiting from, or creating computing machinery. It includes the study and experimentation of algorithmic processes, and development of both hardware and software. Computing has scientific, e ...
* Software engineering
Software engineering is a systematic engineering approach to software development.
A software engineer is a person who applies the principles of software engineering to design, develop, maintain, test, and evaluate computer software. The term ' ...
* Information systems
An information system (IS) is a formal, sociotechnical, organizational system designed to collect, process, store, and distribute information. From a sociotechnical perspective, information systems are composed by four components: task, people ...
A typology
There are different classifications of MCDM problems and methods. A major distinction between MCDM problems is based on whether the solutions are explicitly or implicitly defined. * ''Multiple-criteria evaluation problems'': These problems consist of a finite number of alternatives, explicitly known in the beginning of the solution process. Each alternative is represented by its performance in multiple criteria. The problem may be defined as finding the best alternative for a decision-maker (DM), or finding a set of good alternatives. One may also be interested in "sorting" or "classifying" alternatives. Sorting refers to placing alternatives in a set of preference-ordered classes (such as assigning credit-ratings to countries), and classifying refers to assigning alternatives to non-ordered sets (such as diagnosing patients based on their symptoms). Some of the MCDM methods in this category have been studied in a comparative manner in the book by Triantaphyllou on this subject, 2000. * ''Multiple-criteria design problems (multiple objective mathematical programming problems)'': In these problems, the alternatives are not explicitly known. An alternative (solution) can be found by solving a mathematical model. The number of alternatives is either infinite (countable or not) or finite, but typically exponentially large (in the number of variables ranging over finite domains.) Whether it is an evaluation problem or a design problem, preference information of DMs is required in order to differentiate between solutions. The solution methods for MCDM problems are commonly classified based on the timing of preference information obtained from the DM. There are methods that require the DM's preference information at the start of the process, transforming the problem into essentially a single criterion problem. These methods are said to operate by "prior articulation of preferences". Methods based on estimating a value function or using the concept of "outranking relations", analytical hierarchy process, and some rule-based decision methods try to solve multiple criteria evaluation problems utilizing prior articulation of preferences. Similarly, there are methods developed to solve multiple-criteria design problems using prior articulation of preferences by constructing a value function. Perhaps the most well-known of these methods is goal programming. Once the value function is constructed, the resulting single objective mathematical program is solved to obtain a preferred solution. Some methods require preference information from the DM throughout the solution process. These are referred to as interactive methods or methods that require "progressive articulation of preferences". These methods have been well-developed for both the multiple criteria evaluation (see for example, Geoffrion, Dyer and Feinberg, 1972, and Köksalan and Sagala, 1995 ) and design problems (see Steuer, 1986). Multiple-criteria design problems typically require the solution of a series of mathematical programming models in order to reveal implicitly defined solutions. For these problems, a representation or approximation of "efficient solutions" may also be of interest. This category is referred to as "posterior articulation of preferences", implying that the DM's involvement starts posterior to the explicit revelation of "interesting" solutions (see for example Karasakal and Köksalan, 2009). When the mathematical programming models contain integer variables, the design problems become harder to solve. Multiobjective Combinatorial Optimization (MOCO) constitutes a special category of such problems posing substantial computational difficulty (see Ehrgott and Gandibleux, 2002, for a review).Representations and definitions
The MCDM problem can be represented in the criterion space or the decision space. Alternatively, if different criteria are combined by a weighted linear function, it is also possible to represent the problem in the weight space. Below are the demonstrations of the criterion and weight spaces as well as some formal definitions.Criterion space representation
Let us assume that we evaluate solutions in a specific problem situation using several criteria. Let us further assume that more is better in each criterion. Then, among all possible solutions, we are ideally interested in those solutions that perform well in all considered criteria. However, it is unlikely to have a single solution that performs well in all considered criteria. Typically, some solutions perform well in some criteria and some perform well in others. Finding a way of trading off between criteria is one of the main endeavors in the MCDM literature. Mathematically, the MCDM problem corresponding to the above arguments can be represented as :: :: subject to ::: where is the vector of ''k'' criterion functions (objective functions) and is the feasible set, . If is defined explicitly (by a set of alternatives), the resulting problem is called a multiple-criteria evaluation problem. If is defined implicitly (by a set of constraints), the resulting problem is called a multiple-criteria design problem. The quotation marks are used to indicate that the maximization of a vector is not a well-defined mathematical operation. This corresponds to the argument that we will have to find a way to resolve the trade-off between criteria (typically based on the preferences of a decision maker) when a solution that performs well in all criteria does not exist.Decision space representation
The decision space corresponds to the set of possible decisions that are available to us. The criteria values will be consequences of the decisions we make. Hence, we can define a corresponding problem in the decision space. For example, in designing a product, we decide on the design parameters (decision variables) each of which affects the performance measures (criteria) with which we evaluate our product. Mathematically, a multiple-criteria design problem can be represented in the decision space as follows: : where is the feasible set and is the decision variable vector of size n. A well-developed special case is obtained when is a polyhedron defined by linear inequalities and equalities. If all the objective functions are linear in terms of the decision variables, this variation leads to multiple objective linear programming (MOLP), an important subclass of MCDM problems. There are several definitions that are central in MCDM. Two closely related definitions are those of nondominance (defined based on the criterion space representation) and efficiency (defined based on the decision variable representation). ''Definition 1.'' is nondominated if there does not exist another such that and . Roughly speaking, a solution is nondominated so long as it is not inferior to any other available solution in all the considered criteria. ''Definition 2.'' is efficient if there does not exist another such that and . If an MCDM problem represents a decision situation well, then the most preferred solution of a DM has to be an efficient solution in the decision space, and its image is a nondominated point in the criterion space. Following definitions are also important. ''Definition 3.'' is weakly nondominated if there does not exist another such that . ''Definition 4.'' is weakly efficient if there does not exist another such that . Weakly nondominated points include all nondominated points and some special dominated points. The importance of these special dominated points comes from the fact that they commonly appear in practice and special care is necessary to distinguish them from nondominated points. If, for example, we maximize a single objective, we may end up with a weakly nondominated point that is dominated. The dominated points of the weakly nondominated set are located either on vertical or horizontal planes (hyperplanes) in the criterion space. ''Ideal point'': (in criterion space) represents the best (the maximum for maximization problems and the minimum for minimization problems) of each objective function and typically corresponds to an infeasible solution. ''Nadir point'': (in criterion space) represents the worst (the minimum for maximization problems and the maximum for minimization problems) of each objective function among the points in the nondominated set and is typically a dominated point. The ideal point and the nadir point are useful to the DM to get the "feel" of the range of solutions (although it is not straightforward to find the nadir point for design problems having more than two criteria).Illustrations of the decision and criterion spaces
The following two-variable MOLP problem in the decision variable space will help demonstrate some of the key concepts graphically. :
In Figure 1, the extreme points "e" and "b" maximize the first and second objectives, respectively. The red boundary between those two extreme points represents the efficient set. It can be seen from the figure that, for any feasible solution outside the efficient set, it is possible to improve both objectives by some points on the efficient set. Conversely, for any point on the efficient set, it is not possible to improve both objectives by moving to any other feasible solution. At these solutions, one has to sacrifice from one of the objectives in order to improve the other objective.
Due to its simplicity, the above problem can be represented in criterion space by replacing the with the as follows:
:
In Figure 1, the extreme points "e" and "b" maximize the first and second objectives, respectively. The red boundary between those two extreme points represents the efficient set. It can be seen from the figure that, for any feasible solution outside the efficient set, it is possible to improve both objectives by some points on the efficient set. Conversely, for any point on the efficient set, it is not possible to improve both objectives by moving to any other feasible solution. At these solutions, one has to sacrifice from one of the objectives in order to improve the other objective.
Due to its simplicity, the above problem can be represented in criterion space by replacing the with the as follows:
 ::
::
:: subject to
:::
:::
:::
:::
:::
:::
:::
We present the criterion space graphically in Figure 2. It is easier to detect the nondominated points (corresponding to efficient solutions in the decision space) in the criterion space. The north-east region of the feasible space constitutes the set of nondominated points (for maximization problems).
::
::
:: subject to
:::
:::
:::
:::
:::
:::
:::
We present the criterion space graphically in Figure 2. It is easier to detect the nondominated points (corresponding to efficient solutions in the decision space) in the criterion space. The north-east region of the feasible space constitutes the set of nondominated points (for maximization problems).
Generating nondominated solutions
There are several ways to generate nondominated solutions. We will discuss two of these. The first approach can generate a special class of nondominated solutions whereas the second approach can generate any nondominated solution. * ''Weighted sums'' (Gass & Saaty, 1955) If we combine the multiple criteria into a single criterion by multiplying each criterion with a positive weight and summing up the weighted criteria, then the solution to the resulting single criterion problem is a special efficient solution. These special efficient solutions appear at corner points of the set of available solutions. Efficient solutions that are not at corner points have special characteristics and this method is not capable of finding such points. Mathematically, we can represent this situation as :: = :: subject to ::: By varying the weights, weighted sums can be used for generating efficient extreme point solutions for design problems, and supported (convex nondominated) points for evaluation problems. * ''Achievement scalarizing function'' (Wierzbicki, 1980) Achievement scalarizing functions also combine multiple criteria into a single criterion by weighting them in a very special way. They create rectangular contours going away from a reference point towards the available efficient solutions. This special structure empower achievement scalarizing functions to reach any efficient solution. This is a powerful property that makes these functions very useful for MCDM problems.
Mathematically, we can represent the corresponding problem as
:: = ,
::subject to
:::
The achievement scalarizing function can be used to project any point (feasible or infeasible) on the efficient frontier. Any point (supported or not) can be reached. The second term in the objective function is required to avoid generating inefficient solutions. Figure 3 demonstrates how a feasible point, , and an infeasible point, , are projected onto the nondominated points, and , respectively, along the direction using an achievement scalarizing function. The dashed and solid contours correspond to the objective function contours with and without the second term of the objective function, respectively.
Achievement scalarizing functions also combine multiple criteria into a single criterion by weighting them in a very special way. They create rectangular contours going away from a reference point towards the available efficient solutions. This special structure empower achievement scalarizing functions to reach any efficient solution. This is a powerful property that makes these functions very useful for MCDM problems.
Mathematically, we can represent the corresponding problem as
:: = ,
::subject to
:::
The achievement scalarizing function can be used to project any point (feasible or infeasible) on the efficient frontier. Any point (supported or not) can be reached. The second term in the objective function is required to avoid generating inefficient solutions. Figure 3 demonstrates how a feasible point, , and an infeasible point, , are projected onto the nondominated points, and , respectively, along the direction using an achievement scalarizing function. The dashed and solid contours correspond to the objective function contours with and without the second term of the objective function, respectively.
Solving MCDM problems
Different schools of thought have developed for solving MCDM problems (both of the design and evaluation type). For a bibliometric study showing their development over time, see Bragge, Korhonen, H. Wallenius and J. Wallenius010 010 may refer to:
* 10 (number)
* 8 (number) in octal numeral notation
* Motorola 68010, a microprocessor released by Motorola in 1982
* 010, the telephone area code of Beijing
* 010, the Rotterdam
Rotterdam ( , , , lit. ''The Dam on the ...
''Multiple objective mathematical programming school''
(1) ''Vector maximization'': The purpose of vector maximization is to approximate the nondominated set; originally developed for Multiple Objective Linear Programming problems (Evans and Steuer, 1973; Yu and Zeleny, 1975).
(2) ''Interactive programming'': Phases of computation alternate with phases of decision-making (Benayoun et al., 1971; Geoffrion, Dyer and Feinberg, 1972; Zionts and Wallenius, 1976; Korhonen and Wallenius, 1988). No explicit knowledge of the DM's value function is assumed.
'' Goal programming school''
The purpose is to set apriori target values for goals, and to minimize weighted deviations from these goals. Both importance weights as well as lexicographic pre-emptive weights have been used (Charnes and Cooper, 1961).
''Fuzzy-set theorists''
Fuzzy sets were introduced by Zadeh (1965) as an extension of the classical notion of sets. This idea is used in many MCDM algorithms to model and solve fuzzy problems.
''Ordinal data based methods''
Ordinal data
Ordinal data is a categorical, statistical data type where the variables have natural, ordered categories and the distances between the categories are not known. These data exist on an ordinal scale, one of four levels of measurement described by ...
has a wide application in real-world situations. In this regard, some MCDM methods were designed to handle ordinal data as input data. For example, Ordinal Priority Approach and Qualiflex method.
''Multi-attribute utility theorists''
Multi-attribute utility In decision theory, a multi-attribute utility function is used to represent the preferences of an agent over bundles of goods either under conditions of certainty about the results of any potential choice, or under conditions of uncertainty.
Preli ...
or value functions are elicited and used to identify the most preferred alternative or to rank order the alternatives. Elaborate interview techniques, which exist for eliciting linear additive utility functions and multiplicative nonlinear utility functions, may be used (Keeney and Raiffa, 1976). Another approach is to elicit value functions indirectly by asking the decision-maker a series of pairwise ranking questions involving choosing between hypothetical alternatives ( PAPRIKA method; Hansen and Ombler, 2008).
''French school''
The French school focuses on decision aiding, in particular the ELECTRE family of outranking methods that originated in France during the mid-1960s. The method was first proposed by Bernard Roy (Roy, 1968).
''Evolutionary multiobjective optimization school (EMO)''
EMO algorithms start with an initial population, and update it by using processes designed to mimic natural survival-of-the-fittest principles and genetic variation operators to improve the average population from one generation to the next. The goal is to converge to a population of solutions which represent the nondominated set (Schaffer, 1984; Srinivas and Deb, 1994). More recently, there are efforts to incorporate preference information into the solution process of EMO algorithms (see Deb and Köksalan, 2010).
''Grey system theory Grey relational analysis (GRA) was developed by Deng Julong of Huazhong University of Science and Technology. It is one of the most widely used models of grey system theory. GRA uses a specific concept of information. It defines situations with no ...
based methods''
In the 1980s, Deng Julong
Deng Julong (; January 1933 – June 22, 2013) was a professor of Huazhong University of Science and Technology, Wuhan, China. He is acknowledged as the founder of grey system theory, first proposed in 1982 with the publication of his paper “ ...
proposed Grey System Theory (GST) and its first multiple-attribute decision-making model, called Deng's Grey relational analysis Grey relational analysis (GRA) was developed by Deng Julong of Huazhong University of Science and Technology. It is one of the most widely used models of grey system theory. GRA uses a specific concept of information. It defines situations with no i ...
(GRA) model. Later, the grey systems scholars proposed many GST based methods like Liu Sifeng
Liu Sifeng (; born 15 July 1955) is a Chinese systems engineer. He is the director of the Institute for Grey Systems Studies at Nanjing University of Aeronautics and Astronautics, Nanjing, China. He is best known for his work on grey system t ...
's Absolute GRA model, Grey Target Decision Making (GTDM) and Grey Absolute Decision Analysis (GADA).
'' Analytic hierarchy process (AHP)''
The AHP first decomposes the decision problem into a hierarchy of subproblems. Then the decision-maker evaluates the relative importance of its various elements by pairwise comparisons. The AHP converts these evaluations to numerical values (weights or priorities), which are used to calculate a score for each alternative (Saaty, 1980). A consistency index measures the extent to which the decision-maker has been consistent in her responses. AHP is one of the more controversial techniques listed here, with some researchers in the MCDA community believing it to be flawed.Belton, V, and Stewart, TJ (2002). ''Multiple Criteria Decision Analysis: An Integrated Approach'', Kluwer: Boston. The underlying mathematics is also more complicated, though it has gained some popularity as a result of commercially available software.
Several papers reviewed the application of MCDM techniques in various disciplines such as fuzzy MCDM, classic MCDM, sustainable and renewable energy, VIKOR technique, transportation systems, service quality, TOPSIS method, energy management problems, e-learning, tourism and hospitality, SWARA and WASPAS methods.
MCDM methods
The following MCDM methods are available, many of which are implemented by specializeddecision-making software Decision-making software (DM software) is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
An early example of DM so ...
:
* Aggregated Indices Randomization Method
In applied mathematics and decision making, the aggregated indices randomization method (AIRM) is a modification of a well-known aggregated indices method, targeting complex objects subjected to multi-criteria estimation under uncertainty. AIRM wa ...
(AIRM)
* Analytic hierarchy process
In the theory of decision making, the analytic hierarchy process (AHP), also analytical hierarchy process, is a structured technique for organizing and analyzing complex decisions, based on mathematics and psychology. It was developed by Thoma ...
(AHP)
* Analytic network process
The analytic network process (ANP) is a more general form of the analytic hierarchy process (AHP) used in multi-criteria decision analysis.
AHP structures a decision problem into a hierarchy with a goal, decision criteria, and alternatives, while ...
(ANP)
*Balance Beam process
* Best worst method (BWM)
* Brown–Gibson model
The Brown–Gibson model is one of the many techniques for Multi-criteria decision analysis, multi-attribute decision making. The method was developed in 1972 by P. Brown and D. Gibson.
This is one of the few models which integrates both objectiv ...
* Characteristic Objects METhod
A characteristic is a distinguishing feature of a person or thing. It may refer to:
Computing
* Characteristic (biased exponent), an ambiguous term formerly used by some authors to specify some type of exponent of a floating point number
* Charact ...
(COMET)
* Choosing By Advantages (CBA)
A choice is the range of different things from which a being can choose. The arrival at a choice may incorporate motivators and models. For example, a traveler might choose a route for a journey based on the preference of arriving at a given ...
* Conjoint Value Hierarchy (CVA)
{{Unreferenced, date=December 2009
The conjoint was a basic medical qualification in the United Kingdom administered by the United Examining Board. It is now no longer awarded. The Conjoint Board was superseded in 1994 by the United Examining Board ...
* Data envelopment analysis
Data envelopment analysis (DEA) is a nonparametric method in operations research and economics for the estimation of production frontiers.Charnes et al (1978) DEA has been applied in a large range of fields including international banking, economi ...
* Decision EXpert (DEX)
* Disaggregation – Aggregation Approaches (UTA*, UTAII, UTADIS)
* Rough set
In computer science, a rough set, first described by Polish computer scientist Zdzisław I. Pawlak, is a formal approximation of a crisp set (i.e., conventional set) in terms of a pair of sets which give the ''lower'' and the ''upper'' approxima ...
(Rough set approach)
* Dominance-based rough set approach
The dominance-based rough set approach (DRSA) is an extension of rough set theory for multi-criteria decision analysis (MCDA), introduced by Greco, Matarazzo and Słowiński.
Greco, S., Matarazzo, B., Słowiński, R.: Rough sets theory for multi- ...
(DRSA)
* ELECTRE (Outranking)
* Evaluation Based on Distance from Average Solution
Evaluation is a
systematic determination and assessment of a subject's merit, worth and significance, using criteria governed by a set of standards. It can assist an organization, program, design, project or any other intervention or initiative to ...
(EDAS)
* Evidential reasoning approach (ER)
* Goal programming (GP)
* Grey relational analysis Grey relational analysis (GRA) was developed by Deng Julong of Huazhong University of Science and Technology. It is one of the most widely used models of grey system theory. GRA uses a specific concept of information. It defines situations with no i ...
(GRA)
* Inner product of vectors (IPV)
* Measuring Attractiveness by a categorical Based Evaluation Technique (MACBETH)
* Multi-Attribute Global Inference of Quality
Multi-attribute global inference of quality (MAGIQ) is a multi-criteria decision analysis technique. MAGIQ is based on a hierarchical decomposition of comparison attributes and rating assignment using rank order centroids.
Description
The MAGIQ ...
(MAGIQ)
* Multi-attribute utility theory (MAUT)
* Multi-attribute value theory (MAVT)
* Markovian Multi Criteria Decision Making Markovian is an adjective that may describe:
* In probability theory and statistics, subjects named for Andrey Markov:
** A Markov chain or Markov process, a stochastic model describing a sequence of possible events
** The Markov property, the memo ...
* New Approach to Appraisal
The New Approach to Appraisal (also NATA) was the name given to a multi-criteria decision framework used to appraise transport projects and proposals in the United Kingdom. NATA was built on the well established cost–benefit analysis and envi ...
(NATA)
* Nonstructural Fuzzy Decision Support System (NSFDSS)
* Ordinal Priority Approach (OPA)
* Potentially All Pairwise RanKings of all possible Alternatives #REDIRECT Potentially all pairwise rankings of all possible alternatives
{{R from other capitalisation ...
(PAPRIKA)
* PROMETHEE #REDIRECT Preference ranking organization method for enrichment evaluation #REDIRECT Preference ranking organization method for enrichment evaluation {{R from other capitalisation ...
{{R from other capitalisation ...Simple Multi-Attribute Rating Technique
Simple or SIMPLE may refer to:
*Simplicity, the state or quality of being simple
Arts and entertainment
* ''Simple'' (album), by Andy Yorke, 2008, and its title track
* "Simple" (Florida Georgia Line song), 2018
* "Simple", a song by Johnn ...
(SMART)
* Stratified Multi Criteria Decision Making (SMCDM)
* Stochastic Multicriteria Acceptability Analysis Stochastic multicriteria acceptability analysis (SMAA) is a multiple-criteria decision analysis method for problems with missing or incomplete information.
Description
This means that criteria and preference information can be uncertain, inaccurate ...
(SMAA)
* Superiority and inferiority ranking method
The superiority and inferiority ranking method (or SIR method) is a multi-criteria decision making model (MCDA) which can handle real data and provides six different preference structures for the system user. MCDM is a sub-discipline of operatio ...
(SIR method)
*System Redesigning to Creating Shared Value
A system is a group of interacting or interrelated elements that act according to a set of rules to form a unified whole. A system, surrounded and influenced by its environment, is described by its boundaries, structure and purpose and expressed ...
( SYRCS)
* Technique for the Order of Prioritisation by Similarity to Ideal Solution (TOPSIS)
* Value analysis
Value engineering (VE) is a systematic analysis of the functions of various components and materials to lower the cost of goods, products and services with a tolerable loss of performance or functionality. Value, as defined, ...
(VA)
* Value engineering
Value engineering (VE) is a systematic analysis of the functions of various components and materials to lower the cost of goods, products and services with a tolerable loss of performance or functionality. Value, as defined, ...
(VE)
* VIKOR method
* Weighted product model
The weighted product model (WPM) is a popular multi-criteria decision analysis (MCDA) / multi-criteria decision making (MCDM) method. It is similar to the weighted sum model (WSM). The main difference is that instead of addition in th ...
(WPM)
* Weighted sum model
In decision theory, the weighted sum model (WSM),
also called weighted linear combination (WLC) or simple additive weighting (SAW),
is the best known and simplest multi-criteria decision analysis (MCDA) / multi-criteria decision making method ...
(WSM)
See also
*Architecture tradeoff analysis method In software engineering, architecture tradeoff analysis method (ATAM) is a risk-mitigation process used early in the software development life cycle.
ATAM was developed by the Software Engineering Institute at the Carnegie Mellon University. Its pu ...
* Decision-making
In psychology, decision-making (also spelled decision making and decisionmaking) is regarded as the cognitive process resulting in the selection of a belief or a course of action among several possible alternative options. It could be either r ...
* Decision-making software Decision-making software (DM software) is software for computer applications that help individuals and organisations make choices and take decisions, typically by ranking, prioritizing or choosing from a number of options.
An early example of DM so ...
* Decision-making paradox
The decision-making paradox is a phenomenon related to decision-making and the quest for determining reliable decision-making methods. It was first described by Triantaphyllou , and has been recognized in the related literature as a fundamental p ...
* Decisional balance sheet
A decisional balance sheet or decision balance sheet is a tabular method for representing the pros and cons of different choices and for helping someone decide what to do in a certain circumstance. It is often used in working with ambivalence in p ...
* Multicriteria classification problems
* Rank reversals in decision-making
* Superiority and inferiority ranking method
The superiority and inferiority ranking method (or SIR method) is a multi-criteria decision making model (MCDA) which can handle real data and provides six different preference structures for the system user. MCDM is a sub-discipline of operatio ...
References
Further reading
* * *A Brief History prepared by Steuer and Zionts
*Malakooti, B. (2013). Operations and Production Systems with Multiple Objectives. John Wiley & Sons. {{DEFAULTSORT:Multi-Criteria Decision Analysis Decision analysis Management systems Mathematical optimization Utility sr:Вишекритеријумска оптимизација