Median Operator on:
[Wikipedia]
[Google]
[Amazon]
In

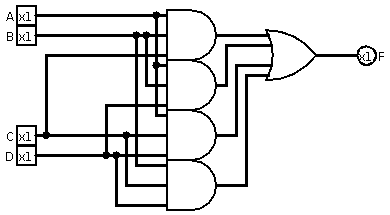 A ''majority gate'' is a
A ''majority gate'' is a
Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variable (mathematics), variables are the truth values ''true'' and ''false'', usually denote ...
, the majority function (also called the median operator) is the Boolean function that evaluates to false when half or more arguments are false and true otherwise, i.e. the value of the function equals the value of the majority of the inputs. Representing true values as 1 and false values as 0, we may use the (real-valued) formula:
:
The "−1/2" in the formula serves to break ties in favor of zeros when the number of arguments ''n'' is even. If the term "−1/2" is omitted, the formula can be used for a function that breaks ties in favor of ones.
Most applications deliberately force an odd number of inputs so they don't have to deal with the question of what happens when exactly half the inputs are 0 and exactly half the inputs are 1. The few systems that calculate the majority function on an even number of inputs are often biased towards "0"—they produce "0" when exactly half the inputs are 0 -- for example, a 4-input majority gate has a 0 output only when two or more 0's appear at its inputs. In a few systems, the tie can be broken randomly.
Boolean circuits

 A ''majority gate'' is a
A ''majority gate'' is a logical gate
A logic gate is an idealized or physical device implementing a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic gate, ...
used in circuit complexity and other applications of Boolean circuits
In computational complexity theory and circuit complexity, a Boolean circuit is a mathematical model for combinational digital logic circuits. A formal language can be decided by a family of Boolean circuits, one circuit for each possible input ...
. A majority gate returns true if and only if more than 50% of its inputs are true.
For instance, in a full adder, the carry output is found by applying a majority function to the three inputs, although frequently this part of the adder is broken down into several simpler logical gates.
Many systems have triple modular redundancy
Triple is used in several contexts to mean "threefold" or a " treble":
Sports
* Triple (baseball), a three-base hit
* A basketball three-point field goal
* A figure skating jump with three rotations
* In bowling terms, three strikes in a row
* I ...
; they use the majority function for majority logic decoding In error detection and correction, majority logic decoding is a method to decode repetition codes, based on the assumption that the largest number of occurrences of a symbol was the transmitted symbol.
Theory
In a binary alphabet made of 0,1, if a ...
to implement error correction
In information theory and coding theory with applications in computer science and telecommunication, error detection and correction (EDAC) or error control are techniques that enable reliable delivery of digital data over unreliable communica ...
.
A major result in circuit complexity asserts that the majority function cannot be computed by AC0 circuits of subexponential size.
Properties
For any ''x'', ''y'', and ''z'', the ternary median operator ⟨''x'', ''y'', ''z''⟩ satisfies the following equations. * ⟨''x'', ''y'', ''y''⟩ = ''y'' * ⟨''x'', ''y'', ''z''⟩ = ⟨''z'', ''x'', ''y''⟩ * ⟨''x'', ''y'', ''z''⟩ = ⟨''x'', ''z'', ''y''⟩ * ⟨⟨''x'', ''w'', ''y''⟩, ''w'', ''z''⟩ = ⟨''x'', ''w'', ⟨''y'', ''w'', ''z''⟩⟩ An abstract system satisfying these as axioms is amedian algebra In mathematics, a median algebra is a set with a ternary operation \langle x,y,z \rangle satisfying a set of axioms which generalise the notions of medians of triples of real numbers and of the Boolean majority function.
The axioms are
# \langl ...
.
Monotone formulae for majority
For ''n'' = 1 the median operator is just the unary identity operation ''x''. For ''n'' = 3 the ternary median operator can be expressed using conjunction and disjunction as ''xy'' + ''yz'' + ''zx''. Remarkably this expression denotes the same operation independently of whether the symbol + is interpreted asinclusive or
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor S ...
or exclusive or.
For an arbitrary ''n'' there exists a monotone formula for majority of size O(''n''5.3). This is proved using probabilistic method. Thus, this formula is non-constructive.
Approaches exist for an explicit formula for majority of polynomial size:
* Take the median from a sorting network, where each compare-and-swap "wire" is simply an OR gate and an AND gate. The Ajtai– Komlós– Szemerédi (AKS) construction is an example.
* Combine the outputs of smaller majority circuits.
* Derandomize the Valiant proof of a monotone formula.
Notes
References
*See also
{{Commonscat-inline, Majority functions *Boolean algebra (structure)
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a gen ...
* Boolean algebras canonically defined
:''Boolean algebras are models of the equational theory of two values; this definition is equivalent to the lattice and ring definitions.''
Boolean algebra is a mathematically rich branch of abstract algebra. ''Stanford Encyclopaedia of Philosoph ...
* Boyer–Moore majority vote algorithm
The Boyer–Moore majority vote algorithm is an algorithm for finding the majority of a sequence of elements using linear time and constant space. It is named after Robert S. Boyer and J Strother Moore, who published it in 1981,. Originally publis ...
* Majority problem (cellular automaton) The majority problem, or density classification task, is the problem of finding one-dimensional cellular automaton rules that accurately perform majority voting.
Using local transition rules, cells cannot know the total count of all the ones in sys ...
Logic gates
Circuit complexity
Boolean algebra