Maximum power transfer theorem on:
[Wikipedia]
[Google]
[Amazon]
In
 The theorem was originally misunderstood (notably by
The theorem was originally misunderstood (notably by  The efficiency is the ratio of the power dissipated by the load resistance to the total power dissipated by the circuit (which includes the voltage source's resistance of as well as ):
Consider three particular cases (note that voltage sources must have some resistance):
* If , then Efficiency approaches 0% if the load resistance approaches zero (a short circuit), since all power is consumed in the source and no power is consumed in the short.
* If , then Efficiency is only 50% if the load resistance equals the source resistance (which is the condition of maximum power transfer).
* If , then Efficiency approaches 100% if the load resistance approaches infinity (though the total power level tends towards zero) or if the source resistance approaches zero. Using a large ratio is called impedance bridging.
The efficiency is the ratio of the power dissipated by the load resistance to the total power dissipated by the circuit (which includes the voltage source's resistance of as well as ):
Consider three particular cases (note that voltage sources must have some resistance):
* If , then Efficiency approaches 0% if the load resistance approaches zero (a short circuit), since all power is consumed in the source and no power is consumed in the short.
* If , then Efficiency is only 50% if the load resistance equals the source resistance (which is the condition of maximum power transfer).
* If , then Efficiency approaches 100% if the load resistance approaches infinity (though the total power level tends towards zero) or if the source resistance approaches zero. Using a large ratio is called impedance bridging.
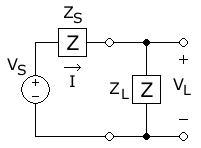 In this diagram, AC power is being transferred from the source, with phasor magnitude of voltage (positive peak voltage) and fixed source impedance (S for source), to a load with impedance (L for load), resulting in a (positive) magnitude of the current phasor . This magnitude results from dividing the magnitude of the source voltage by the magnitude of the total circuit impedance:
The average power dissipated in the load is the square of the current multiplied by the resistive portion (the real part) of the load impedance :
where and denote the resistances, that is the real parts, and and denote the reactances, that is the imaginary parts, of respectively the source and load impedances and .
To determine, for a given source, the voltage and the impedance the value of the load impedance for which this expression for the power yields a maximum, one first finds, for each fixed positive value of , the value of the reactive term for which the denominator:
is a minimum. Since reactances can be negative, this is achieved by adapting the load reactance to:
This reduces the above equation to:
and it remains to find the value of which maximizes this expression. This problem has the same form as in the purely resistive case, and the maximizing condition therefore is
The two maximizing conditions:
*
*
describe the complex conjugate of the source impedance, denoted by and thus can be concisely combined to:
In this diagram, AC power is being transferred from the source, with phasor magnitude of voltage (positive peak voltage) and fixed source impedance (S for source), to a load with impedance (L for load), resulting in a (positive) magnitude of the current phasor . This magnitude results from dividing the magnitude of the source voltage by the magnitude of the total circuit impedance:
The average power dissipated in the load is the square of the current multiplied by the resistive portion (the real part) of the load impedance :
where and denote the resistances, that is the real parts, and and denote the reactances, that is the imaginary parts, of respectively the source and load impedances and .
To determine, for a given source, the voltage and the impedance the value of the load impedance for which this expression for the power yields a maximum, one first finds, for each fixed positive value of , the value of the reactive term for which the denominator:
is a minimum. Since reactances can be negative, this is achieved by adapting the load reactance to:
This reduces the above equation to:
and it remains to find the value of which maximizes this expression. This problem has the same form as in the purely resistive case, and the maximizing condition therefore is
The two maximizing conditions:
*
*
describe the complex conjugate of the source impedance, denoted by and thus can be concisely combined to:
''Conjugate matching versus reflectionless matching''
( PDF) taken fro
''Electromagnetic Waves and Antennas''
Circuit theorems Electrical engineering
electrical engineering
Electrical engineering is an engineering discipline concerned with the study, design, and application of equipment, devices, and systems that use electricity, electronics, and electromagnetism. It emerged as an identifiable occupation in the l ...
, the maximum power transfer theorem states that, to obtain ''maximum'' external power from a power source with internal resistance, the resistance of the load must equal the resistance of the source as viewed from its output terminals. Moritz von Jacobi published the maximum power (transfer) theorem around 1840; it is also referred to as "Jacobi's law".
The theorem
In mathematics and formal logic, a theorem is a statement (logic), statement that has been Mathematical proof, proven, or can be proven. The ''proof'' of a theorem is a logical argument that uses the inference rules of a deductive system to esta ...
results in maximum ''power'' transfer from the power source to the load, but not maximum ''efficiency
Efficiency is the often measurable ability to avoid making mistakes or wasting materials, energy, efforts, money, and time while performing a task. In a more general sense, it is the ability to do things well, successfully, and without waste.
...
'' of useful power out of total power consumed. If the load resistance is made larger than the source resistance, then efficiency increases (since a higher percentage of the source power is transferred to the load), but the ''magnitude'' of the load power decreases (since the total circuit resistance increases). If the load resistance is made smaller than the source resistance, then efficiency decreases (since most of the power ends up being dissipated in the source). Although the total power dissipated increases (due to a lower total resistance), the amount dissipated in the load decreases.
The theorem states how to choose (so as to maximize power transfer) the load resistance, once the source resistance is given. It is a common misconception to apply the theorem in the opposite scenario. It does ''not'' say how to choose the source resistance for a given load resistance. In fact, the source resistance that maximizes power transfer from a voltage source is always zero (the hypothetical ideal voltage source), regardless of the value of the load resistance.
The theorem can be extended to alternating current
Alternating current (AC) is an electric current that periodically reverses direction and changes its magnitude continuously with time, in contrast to direct current (DC), which flows only in one direction. Alternating current is the form in w ...
circuits that include reactance, and states that maximum power transfer occurs when the load impedance is equal to the complex conjugate of the source impedance.
The mathematics of the theorem also applies to other physical interactions, such as:
* mechanical collisions between two objects,
* the sharing of charge between two capacitors,
* liquid flow between two cylinders,
* the transmission and reflection of light at the boundary between two media.
Maximizing power transfer versus power efficiency
Joule
The joule ( , or ; symbol: J) is the unit of energy in the International System of Units (SI). In terms of SI base units, one joule corresponds to one kilogram- metre squared per second squared One joule is equal to the amount of work d ...
) to imply that a system consisting of an electric motor driven by a battery could not be more than 50% efficient, since the power dissipated as heat in the battery would always be equal to the power delivered to the motor when the impedances were matched.
In 1880 this assumption was shown to be false by either Edison or his colleague Francis Robbins Upton, who realized that maximum efficiency was not the same as maximum power transfer.
To achieve maximum efficiency, the resistance of the source (whether a battery or a dynamo) could be (or should be) made as close to zero as possible. Using this new understanding, they obtained an efficiency of about 90%, and proved that the electric motor
An electric motor is a machine that converts electrical energy into mechanical energy. Most electric motors operate through the interaction between the motor's magnetic field and electric current in a electromagnetic coil, wire winding to gene ...
was a practical alternative to the heat engine.Impedance matching
A related concept is reflectionless impedance matching. Inradio
Radio is the technology of communicating using radio waves. Radio waves are electromagnetic waves of frequency between 3 hertz (Hz) and 300 gigahertz (GHz). They are generated by an electronic device called a transmitter connec ...
frequency transmission line
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmis ...
s, and other electronics
Electronics is a scientific and engineering discipline that studies and applies the principles of physics to design, create, and operate devices that manipulate electrons and other Electric charge, electrically charged particles. It is a subfield ...
, there is often a requirement to match the source impedance (at the transmitter) to the load impedance (such as an antenna) to avoid reflections in the transmission line
In electrical engineering, a transmission line is a specialized cable or other structure designed to conduct electromagnetic waves in a contained manner. The term applies when the conductors are long enough that the wave nature of the transmis ...
.
Calculus-based proof for purely resistive circuits
In the simplified model of powering a load with resistance by a source with voltage and source resistance , then byOhm's law
Ohm's law states that the electric current through a Electrical conductor, conductor between two Node (circuits), points is directly Proportionality (mathematics), proportional to the voltage across the two points. Introducing the constant of ...
the resulting current is simply the source voltage divided by the total circuit resistance:
The power dissipated in the load is the square of the current multiplied by the resistance:
The value of for which this expression is a maximum could be calculated by differentiating it, but it is easier to calculate the value of for which the denominator:
is a minimum. The result will be the same in either case. Differentiating the denominator with respect to :
For a maximum or minimum, the first derivative is zero, so
or
In practical resistive circuits, and are both positive, so the positive sign in the above is the correct solution.
To find out whether this solution is a minimum or a maximum, the denominator expression is differentiated again:
This is always positive for positive values of and , showing that the denominator is a minimum, and the power is therefore a maximum, when:
The above proof assumes fixed source resistance . When the source resistance can be varied, power transferred to the load can be increased by reducing . For example, a 100 Volt source with an of will deliver 250 watts of power to a load; reducing to increases the power delivered to 1000 watts.
Note that this shows that maximum power transfer can also be interpreted as the load voltage being equal to one-half of the Thevenin voltage equivalent of the source.
In reactive circuits
The power transfer theorem also applies when the source and/or load are not purely resistive. A refinement of the maximum power theorem says that any reactive components of source and load should be of equal magnitude but opposite sign. (''See below for a derivation.'') * This means that the source and load impedances should be '' complex conjugates'' of each other. * In the case of purely resistive circuits, the two concepts are identical. Physically realizable sources and loads are not usually purely resistive, having some inductive or capacitive components, and so practical applications of this theorem, under the name of complex conjugate impedance matching, do, in fact, exist. If the source is totally inductive (capacitive), then a totally capacitive (inductive) load, in the absence of resistive losses, would receive 100% of the energy from the source but send it back after a quarter cycle. The resultant circuit is nothing other than a resonant LC circuit in which the energy continues to oscillate to and fro. This oscillation is called reactive power. Power factor correction (where an inductive reactance is used to "balance out" a capacitive one), is essentially the same idea as complex conjugate impedance matching although it is done for entirely different reasons. For a fixed reactive ''source'', the maximum power theorem maximizes the real power (P) delivered to the load by complex conjugate matching the load to the source. For a fixed reactive ''load'', power factor correction minimizes the apparent power (S) (and unnecessary current) conducted by the transmission lines, while maintaining the same amount of real power transfer. This is done by adding a reactance to the load to balance out the load's own reactance, changing the reactive load impedance into a resistive load impedance.Proof
 In this diagram, AC power is being transferred from the source, with phasor magnitude of voltage (positive peak voltage) and fixed source impedance (S for source), to a load with impedance (L for load), resulting in a (positive) magnitude of the current phasor . This magnitude results from dividing the magnitude of the source voltage by the magnitude of the total circuit impedance:
The average power dissipated in the load is the square of the current multiplied by the resistive portion (the real part) of the load impedance :
where and denote the resistances, that is the real parts, and and denote the reactances, that is the imaginary parts, of respectively the source and load impedances and .
To determine, for a given source, the voltage and the impedance the value of the load impedance for which this expression for the power yields a maximum, one first finds, for each fixed positive value of , the value of the reactive term for which the denominator:
is a minimum. Since reactances can be negative, this is achieved by adapting the load reactance to:
This reduces the above equation to:
and it remains to find the value of which maximizes this expression. This problem has the same form as in the purely resistive case, and the maximizing condition therefore is
The two maximizing conditions:
*
*
describe the complex conjugate of the source impedance, denoted by and thus can be concisely combined to:
In this diagram, AC power is being transferred from the source, with phasor magnitude of voltage (positive peak voltage) and fixed source impedance (S for source), to a load with impedance (L for load), resulting in a (positive) magnitude of the current phasor . This magnitude results from dividing the magnitude of the source voltage by the magnitude of the total circuit impedance:
The average power dissipated in the load is the square of the current multiplied by the resistive portion (the real part) of the load impedance :
where and denote the resistances, that is the real parts, and and denote the reactances, that is the imaginary parts, of respectively the source and load impedances and .
To determine, for a given source, the voltage and the impedance the value of the load impedance for which this expression for the power yields a maximum, one first finds, for each fixed positive value of , the value of the reactive term for which the denominator:
is a minimum. Since reactances can be negative, this is achieved by adapting the load reactance to:
This reduces the above equation to:
and it remains to find the value of which maximizes this expression. This problem has the same form as in the purely resistive case, and the maximizing condition therefore is
The two maximizing conditions:
*
*
describe the complex conjugate of the source impedance, denoted by and thus can be concisely combined to:
See also
* Maximum power point trackingNotes
References
*H.W. Jackson (1959) Introduction to Electronic Circuits, Prentice-Hall.External links
''Conjugate matching versus reflectionless matching''
( PDF) taken fro
''Electromagnetic Waves and Antennas''
Circuit theorems Electrical engineering