MANOVA

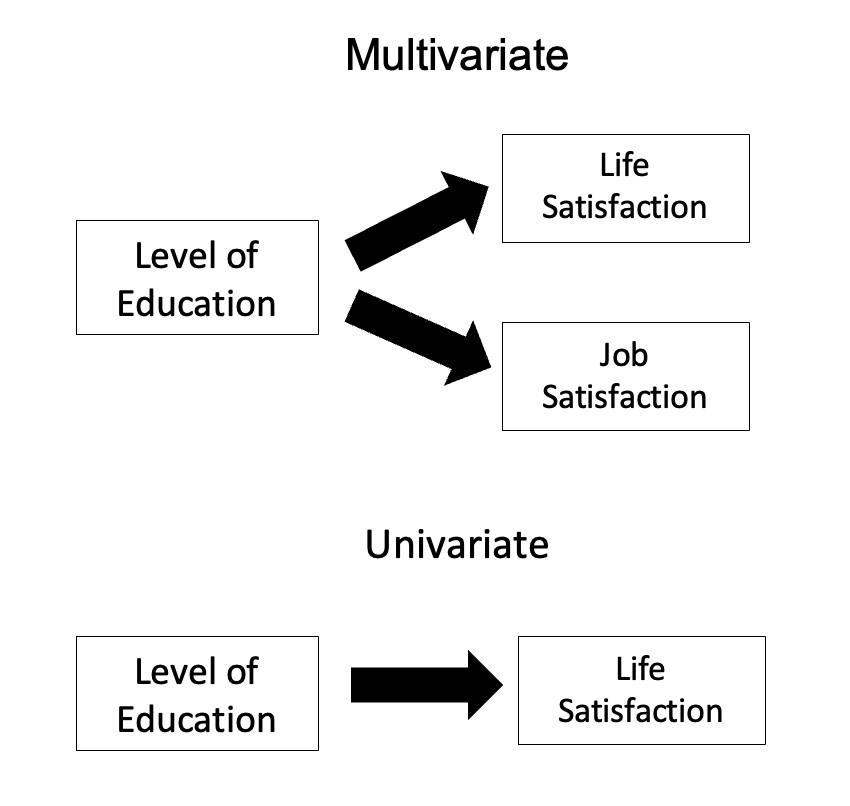In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately.

Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers.

Relationship with ANOVA

MANOVA is a generalized form of univariate analysis of variance (ANOVA), although, unlike univariate ANOVA, it uses the covariance between outcome variables in testing the statistical significance of the mean differences.

Where sums of squares appear in univariate analysis of variance, in multivariate analysis of variance certain positive-definite matrices appear. The diagonal entries are the same kinds of sums of squares that appear in univariate ANOVA. The off-diagonal entries are corresponding sums of products. Under normality assumptions about error distributions, the counterpart of the sum of squares due to error has a Wishart distribution.

MANOVA is based on the product of model variance matrix, $\Sigma_\text$ and inverse of the error variance matrix, $\Sigma_\text^$, or $A=\Sigma_\text \times \Sigma_\text^$. The hypothesis that $\Sigma_\text = \Sigma_\text$ implies that the product $A \sim I$. Invariance considerations imply the MANOVA statistic should be a measure of magnitude of the singular value decomposition of this matrix product, but there is no unique choice owing to the multi-dimensional nature of the alternative hypothesis.

The most common statistics are summaries based on the roots (or eigenvalues) $\lambda_p$ of the $A$ matrix:
* Samuel Stanley Wilks' $\Lambda_\text = \prod_(1/(1 + \lambda_)) = \det(I + A)^ = \det(\Sigma_\text)/\det(\Sigma_\text + \Sigma_\text)$ distributed as lambda (Λ)
* the K. C. Sreedharan Pillai–M. S. Bartlett trace, $\Lambda_\text = \sum_(\lambda_p/(1 + \lambda_p)) = \operatorname(A(I + A)^)$
* the Lawley– Hotelling trace, $\Lambda_\text = \sum_(\lambda_) = \operatorname(A)$
* Roy's greatest root (also called ''Roy's largest root''), $\Lambda_\text = \max_p(\lambda_p)$

Discussion continues over the merits of each, although the greatest root leads only to a bound on significance which is not generally of practical interest. A further complication is that, except for the Roy's greatest root, the distribution of these statistics under the null hypothesis is not straightforward and can only be approximated except in a few low-dimensional cases.
An algorithm for the distribution of the Roy's largest root under the null hypothesis was derived in while the distribution under the alternative is studied in.

The best-known approximation for Wilks' lambda was derived by C. R. Rao.

In the case of two groups, all the statistics are equivalent and the test reduces to Hotelling's T-square.

Correlation of dependent variables

MANOVA's power is affected by the correlations of the dependent variables and by the effect sizes associated with those variables. For example, when there are two groups and two dependent variables, MANOVA's power is lowest when the correlation equals the ratio of the smaller to the larger standardized effect size.

See also

*Discriminant function analysis
* Canonical correlation analysis
* Multivariate analysis of variance (Wikiversity)
* Repeated measures design

References

External links

Multivariate Analysis of Variance (MANOVA) by Aaron French, Marcelo Macedo, John Poulsen, Tyler Waterson and Angela Yu, San Francisco State University

What is a MANOVA test used for?

{{Experimental design

Analysis of variance
Design of experiments