|
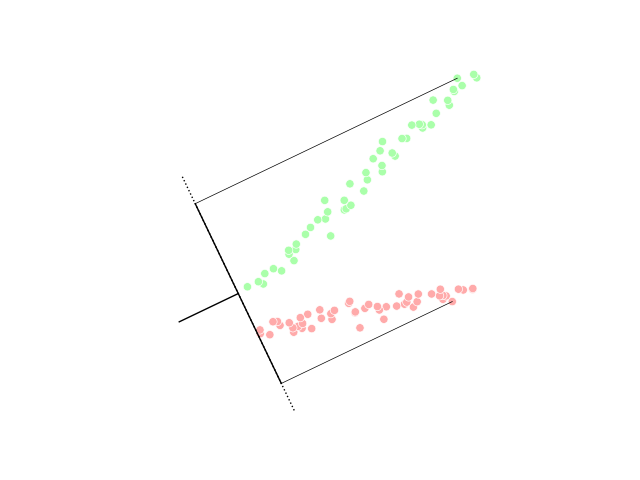
Discriminant Function Analysis
Linear discriminant analysis (LDA), normal discriminant analysis (NDA), or discriminant function analysis is a generalization of Fisher's linear discriminant, a method used in statistics and other fields, to find a linear combination of features that characterizes or separates two or more classes of objects or events. The resulting combination may be used as a linear classifier, or, more commonly, for dimensionality reduction before later statistical classification, classification. LDA is closely related to analysis of variance (ANOVA) and regression analysis, which also attempt to express one dependent variable as a linear combination of other features or measurements. However, ANOVA uses categorical variable, categorical independent variables and a continuous variable, continuous dependent variable, whereas discriminant analysis has continuous independent variables and a categorical dependent variable (''i.e.'' the class label). Logistic regression and probit regression are more ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistics
Statistics (from German: '' Statistik'', "description of a state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a scientific, industrial, or social problem, it is conventional to begin with a statistical population or a statistical model to be studied. Populations can be diverse groups of people or objects such as "all people living in a country" or "every atom composing a crystal". Statistics deals with every aspect of data, including the planning of data collection in terms of the design of surveys and experiments.Dodge, Y. (2006) ''The Oxford Dictionary of Statistical Terms'', Oxford University Press. When census data cannot be collected, statisticians collect data by developing specific experiment designs and survey samples. Representative sampling assures that inferences and conclusions can reasonably extend from the sample to the population as a whole. An ex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cluster Analysis
Cluster analysis or clustering is the task of grouping a set of objects in such a way that objects in the same group (called a cluster) are more similar (in some sense) to each other than to those in other groups (clusters). It is a main task of exploratory data analysis, and a common technique for statistical data analysis, used in many fields, including pattern recognition, image analysis, information retrieval, bioinformatics, data compression, computer graphics and machine learning. Cluster analysis itself is not one specific algorithm, but the general task to be solved. It can be achieved by various algorithms that differ significantly in their understanding of what constitutes a cluster and how to efficiently find them. Popular notions of clusters include groups with small distances between cluster members, dense areas of the data space, intervals or particular statistical distributions. Clustering can therefore be formulated as a multi-objective optimization probl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dot Product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors), and returns a single number. In Euclidean geometry, the dot product of the Cartesian coordinates of two vectors is widely used. It is often called the inner product (or rarely projection product) of Euclidean space, even though it is not the only inner product that can be defined on Euclidean space (see Inner product space for more). Algebraically, the dot product is the sum of the products of the corresponding entries of the two sequences of numbers. Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. These definitions are equivalent when using Cartesian coordinates. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hermitian Matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th row and -th column, for all indices and : or in matrix form: A \text \quad \iff \quad A = \overline . Hermitian matrices can be understood as the complex extension of real symmetric matrices. If the conjugate transpose of a matrix A is denoted by A^\mathsf, then the Hermitian property can be written concisely as Hermitian matrices are named after Charles Hermite, who demonstrated in 1855 that matrices of this form share a property with real symmetric matrices of always having real eigenvalues. Other, equivalent notations in common use are A^\mathsf = A^\dagger = A^\ast, although note that in quantum mechanics, A^\ast typically means the complex conjugate only, and not the conjugate transpose. Alternative characterizations Her ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
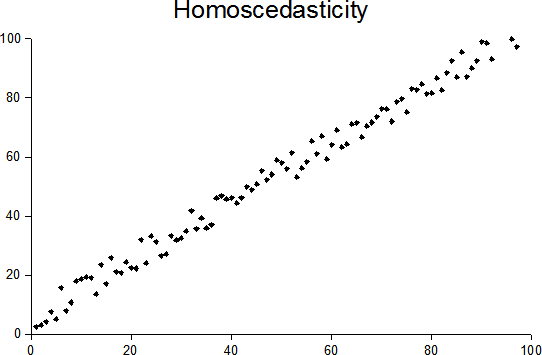
Homoscedastic
In statistics, a sequence (or a vector) of random variables is homoscedastic () if all its random variables have the same finite variance. This is also known as homogeneity of variance. The complementary notion is called heteroscedasticity. The spellings ''homoskedasticity'' and ''heteroskedasticity'' are also frequently used. Assuming a variable is homoscedastic when in reality it is heteroscedastic () results in unbiased but inefficient point estimates and in biased estimates of standard errors, and may result in overestimating the goodness of fit as measured by the Pearson coefficient. The existence of heteroscedasticity is a major concern in regression analysis and the analysis of variance, as it invalidates statistical tests of significance that assume that the modelling errors all have the same variance. While the ordinary least squares estimator is still unbiased in the presence of heteroscedasticity, it is inefficient and generalized least squares should be used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadratic Classifier
In statistics, a quadratic classifier is a statistical classifier that uses a quadratic decision surface to separate measurements of two or more classes of objects or events. It is a more general version of the linear classifier. The classification problem Statistical classification considers a set of vectors of observations x of an object or event, each of which has a known type ''y''. This set is referred to as the training set. The problem is then to determine, for a given new observation vector, what the best class should be. For a quadratic classifier, the correct solution is assumed to be quadratic in the measurements, so ''y'' will be decided based on : \mathbf + \mathbf + c In the special case where each observation consists of two measurements, this means that the surfaces separating the classes will be conic sections (''i.e.'' either a line, a circle or ellipse, a parabola or a hyperbola). In this sense, we can state that a quadratic model is a generalization of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables. If the greater values of one variable mainly correspond with the greater values of the other variable, and the same holds for the lesser values (that is, the variables tend to show similar behavior), the covariance is positive. In the opposite case, when the greater values of one variable mainly correspond to the lesser values of the other, (that is, the variables tend to show opposite behavior), the covariance is negative. The sign of the covariance therefore shows the tendency in the linear relationship between the variables. The magnitude of the covariance is not easy to interpret because it is not normalized and hence depends on the magnitudes of the variables. The normalized version of the covariance, the correlation coefficient, however, shows by its magnitude the strength of the linear relation. A distinction must be made between (1) the covariance of two ran ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariate Normal Distribution
In probability theory and statistics, the multivariate normal distribution, multivariate Gaussian distribution, or joint normal distribution is a generalization of the one-dimensional ( univariate) normal distribution to higher dimensions. One definition is that a random vector is said to be ''k''-variate normally distributed if every linear combination of its ''k'' components has a univariate normal distribution. Its importance derives mainly from the multivariate central limit theorem. The multivariate normal distribution is often used to describe, at least approximately, any set of (possibly) correlated real-valued random variables each of which clusters around a mean value. Definitions Notation and parameterization The multivariate normal distribution of a ''k''-dimensional random vector \mathbf = (X_1,\ldots,X_k)^ can be written in the following notation: : \mathbf\ \sim\ \mathcal(\boldsymbol\mu,\, \boldsymbol\Sigma), or to make it explicitly known that ''X ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability Density Function
In probability theory, a probability density function (PDF), or density of a continuous random variable, is a function whose value at any given sample (or point) in the sample space (the set of possible values taken by the random variable) can be interpreted as providing a ''relative likelihood'' that the value of the random variable would be close to that sample. Probability density is the probability per unit length, in other words, while the ''absolute likelihood'' for a continuous random variable to take on any particular value is 0 (since there is an infinite set of possible values to begin with), the value of the PDF at two different samples can be used to infer, in any particular draw of the random variable, how much more likely it is that the random variable would be close to one sample compared to the other sample. In a more precise sense, the PDF is used to specify the probability of the random variable falling ''within a particular range of values'', as opposed ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Training Set
In machine learning, a common task is the study and construction of algorithms that can learn from and make predictions on data. Such algorithms function by making data-driven predictions or decisions, through building a mathematical model from input data. These input data used to build the model are usually divided in multiple data sets. In particular, three data sets are commonly used in different stages of the creation of the model: training, validation and test sets. The model is initially fit on a training data set, which is a set of examples used to fit the parameters (e.g. weights of connections between neurons in artificial neural networks) of the model. The model (e.g. a naive Bayes classifier) is trained on the training data set using a supervised learning method, for example using optimization methods such as gradient descent or stochastic gradient descent. In practice, the training data set often consists of pairs of an input vector (or scalar) and the correspo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
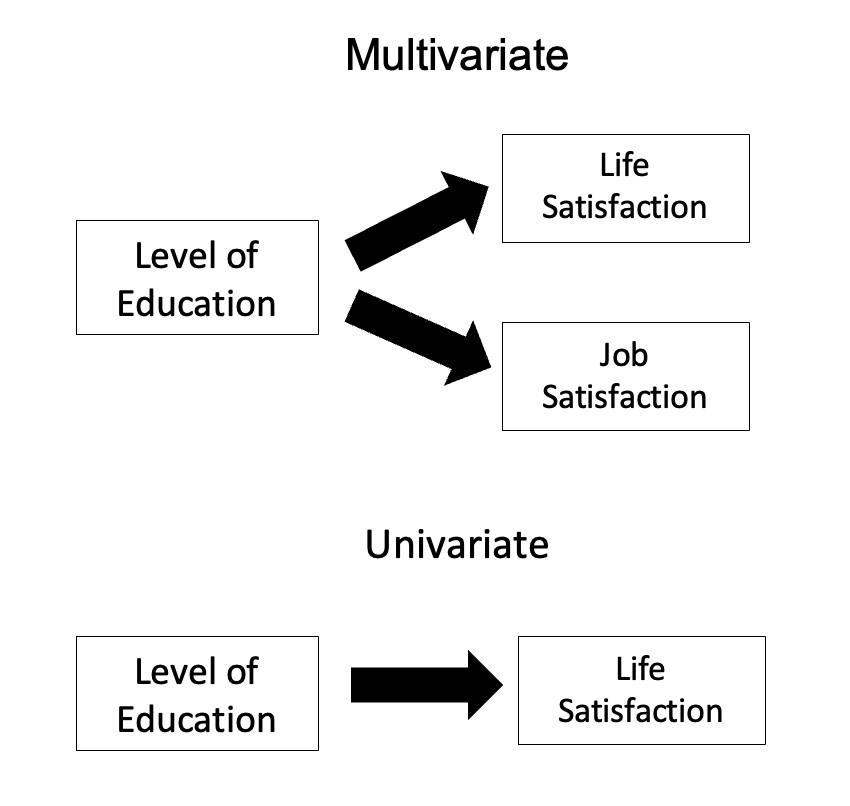
MANOVA
In statistics, multivariate analysis of variance (MANOVA) is a procedure for comparing multivariate sample means. As a multivariate procedure, it is used when there are two or more dependent variables, and is often followed by significance tests involving individual dependent variables separately. Without relation to the image, the dependent variables may be k life satisfactions scores measured at sequential time points and p job satisfaction scores measured at sequential time points. In this case there are k+p dependent variables whose linear combination follows a multivariate normal distribution, multivariate variance-covariance matrix homogeneity, and linear relationship, no multicollinearity, and each without outliers. Relationship with ANOVA MANOVA is a generalized form of univariate analysis of variance (ANOVA), although, unlike univariate ANOVA, it uses the covariance between outcome variables in testing the statistical significance of the mean differences. Where su ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |