M-ary Tree on:
[Wikipedia]
[Google]
[Amazon]
 In
In
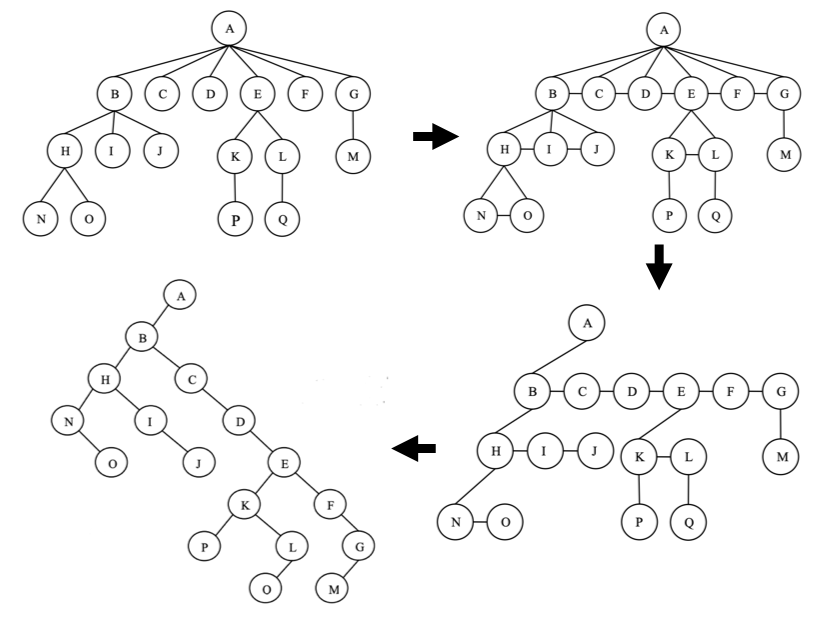 Using an array for representing a ''m-''ary tree is inefficient, because most of the nodes in practical applications contain less than ''m'' children. As a result, this fact leads to a sparse array with large unused space in the memory. Converting an arbitrary ''m-''ary tree to a binary tree would only increase the height of the tree by a constant factor and would not affect the overall worst-case time complexity. In other words, since .
First, we link all the immediate children nodes of a given parent node together in order to form a link list. Then, we keep the link from the parent to the first (i.e., the leftmost) child and remove all the other links to the rest of the children. We repeat this process for all the children (if they have any children) until we have processed all the internal nodes and rotate the tree by 45 degrees clockwise. The tree obtained is the desired binary tree obtained from the given ''m''-ary tree.
Using an array for representing a ''m-''ary tree is inefficient, because most of the nodes in practical applications contain less than ''m'' children. As a result, this fact leads to a sparse array with large unused space in the memory. Converting an arbitrary ''m-''ary tree to a binary tree would only increase the height of the tree by a constant factor and would not affect the overall worst-case time complexity. In other words, since .
First, we link all the immediate children nodes of a given parent node together in order to form a link list. Then, we keep the link from the parent to the first (i.e., the leftmost) child and remove all the other links to the rest of the children. We repeat this process for all the children (if they have any children) until we have processed all the internal nodes and rotate the tree by 45 degrees clockwise. The tree obtained is the desired binary tree obtained from the given ''m''-ary tree.
 ''m''-ary trees can also be stored in breadth-first order as an
''m''-ary trees can also be stored in breadth-first order as an
 Compared to array-based implementation, this implementation method has superior space complexity of .
Compared to array-based implementation, this implementation method has superior space complexity of .
 The problem with this representation is that listing all bit strings in lexicographic order would mean two successive strings might represent two trees that are lexicographically very different. Therefore, enumeration over binary strings would not necessarily result in an ordered generation of all ''m-''ary trees. A better representation is based on an integer string that indicates the number of zeroes between successive ones, known as ''Simple Zero Sequence''. is a Simple Zero Sequence corresponding to the bit sequence where ''j'' is the number of zeroes needed at the tail end of the sequence to make the string have the appropriate length. For example, is the simple zero sequence representation of the above figure. A more compact representation of ''00433'' is , which is called ''zero sequence'', which duplicate bases cannot be adjacent. This new representation allows to construct a next valid sequence in .
A simple zero sequence is valid if
That is to say that number of zeros in the bit sequence of a ''m''-ary tree cannot exceed the total number of null pointers (i.e., pointers without any child node attached to them). This summation is putting restriction on nodes so that there is room for adding the without creating an invalid structure (i.e. having an available null pointer to attached the last node to it).
The table below shows the list of all valid simple zero sequences of all ''3''-ary trees with 4 nodes:
Starting from the bottom right of the table (i.e., "000"), there is a ''backbone template'' that governs the generation of the possible ordered trees starting from "000" to "006". The backbone template for this group ("00X") is depicted below, where an additional node is added in the positions labeled "x".
The problem with this representation is that listing all bit strings in lexicographic order would mean two successive strings might represent two trees that are lexicographically very different. Therefore, enumeration over binary strings would not necessarily result in an ordered generation of all ''m-''ary trees. A better representation is based on an integer string that indicates the number of zeroes between successive ones, known as ''Simple Zero Sequence''. is a Simple Zero Sequence corresponding to the bit sequence where ''j'' is the number of zeroes needed at the tail end of the sequence to make the string have the appropriate length. For example, is the simple zero sequence representation of the above figure. A more compact representation of ''00433'' is , which is called ''zero sequence'', which duplicate bases cannot be adjacent. This new representation allows to construct a next valid sequence in .
A simple zero sequence is valid if
That is to say that number of zeros in the bit sequence of a ''m''-ary tree cannot exceed the total number of null pointers (i.e., pointers without any child node attached to them). This summation is putting restriction on nodes so that there is room for adding the without creating an invalid structure (i.e. having an available null pointer to attached the last node to it).
The table below shows the list of all valid simple zero sequences of all ''3''-ary trees with 4 nodes:
Starting from the bottom right of the table (i.e., "000"), there is a ''backbone template'' that governs the generation of the possible ordered trees starting from "000" to "006". The backbone template for this group ("00X") is depicted below, where an additional node is added in the positions labeled "x".
 Once one has exhausted all possible positions in the backbone template, a new template will be constructed by shifting the 3rd node one position to the right as depicted below, and the same enumeration would occur until all possible positions labeled "X" is exhausted.
Once one has exhausted all possible positions in the backbone template, a new template will be constructed by shifting the 3rd node one position to the right as depicted below, and the same enumeration would occur until all possible positions labeled "X" is exhausted.
 Going back to the table of enumeration of all ''m''-ary trees, where and , we can easily observe the apparent jump from "006" to "010" can be explained trivially in an algorithmic fashion as depicted below:
Going back to the table of enumeration of all ''m''-ary trees, where and , we can easily observe the apparent jump from "006" to "010" can be explained trivially in an algorithmic fashion as depicted below:
 The pseudocode for this enumeration is given below:
Procedure NEXT(''s''1, ''s''2, …, ''s''''n''−1)
if ''si'' = 0 for all ''i'' then
finished
else
''i'' ← max
''si'' ← ''si'' − 1
if ''i'' < ''n'' − 1 then
''si'' ← (''i'' + 1) ⋅ (''m'' − 1) − sum(''sj'')
end if
for ''j'' ← ''i'' + 2, ''i'' + 3, …, ''n'' − 1
''sj'' ← ''k'' − 1
end if
end
The pseudocode for this enumeration is given below:
Procedure NEXT(''s''1, ''s''2, …, ''s''''n''−1)
if ''si'' = 0 for all ''i'' then
finished
else
''i'' ← max
''si'' ← ''si'' − 1
if ''i'' < ''n'' − 1 then
''si'' ← (''i'' + 1) ⋅ (''m'' − 1) − sum(''sj'')
end if
for ''j'' ← ''i'' + 2, ''i'' + 3, …, ''n'' − 1
''sj'' ← ''k'' − 1
end if
end
 Convert an m-ary tree to left-tree
for ''i'' = 1...''n'':
for ''t'' = 2...''m'':
while ''t'' child of node at depth ''i'' ≠ 1:
L-t rotation at nodes at depth ''i''
end while
end for
end for
A ''right-t rotation'' at ''d'' is the inverse of this operation. The ''left chain'' of ''T'' is a sequence of nodes such that is the root and all nodes except have one child connected to their left most (i.e.,
Convert an m-ary tree to left-tree
for ''i'' = 1...''n'':
for ''t'' = 2...''m'':
while ''t'' child of node at depth ''i'' ≠ 1:
L-t rotation at nodes at depth ''i''
end while
end for
end for
A ''right-t rotation'' at ''d'' is the inverse of this operation. The ''left chain'' of ''T'' is a sequence of nodes such that is the root and all nodes except have one child connected to their left most (i.e.,
 In
In graph theory
In mathematics, graph theory is the study of '' graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of '' vertices'' (also called ''nodes'' or ''points'') which are conn ...
, an ''m''-ary tree (also known as ''n''-ary, ''k''-ary or ''k''-way tree) is a rooted tree
In botany, a tree is a perennial plant with an elongated stem, or trunk, usually supporting branches and leaves. In some usages, the definition of a tree may be narrower, including only woody plants with secondary growth, plants that are ...
in which each node has no more than ''m'' children. A binary tree
In computer science, a binary tree is a k-ary k = 2 tree data structure in which each node has at most two children, which are referred to as the ' and the '. A recursive definition using just set theory notions is that a (non-empty) binar ...
is the special case where ''m'' = 2, and a ternary tree is another case with ''m'' = 3 that limits its children to three.
Types of ''m''-ary trees
* A full ''m''-ary tree is an ''m''-ary tree where within each level every node has either 0 or ''m'' children. * A complete ''m''-ary tree is an ''m''-ary tree which is maximally space efficient. It must be completely filled on every level except for the last level. However, if the last level is not complete, then all nodes of the tree must be "as far left as possible". * A perfect ''m''-ary tree is a full ''m''-ary tree in which allleaf node
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be con ...
s are at the same depth.
Properties of ''m''-ary trees
* For an ''m''-ary tree with height ''h'', the upper bound for the maximum number of leaves is . * The height ''h ''of an ''m''-ary tree does not include the root node, with a tree containing only a root node having a height of 0. * The height of a tree is equal to the maximum depth ''D'' of any node in the tree. * The total number of nodes in a perfect ''m''-ary tree is , while the height ''h'' is By the definition of Big-Ω, the maximum depth * The height of a complete ''m''-ary tree with ''n'' nodes is . * The total number of possible ''m''-ary tree with ''n'' nodes is (which is aCatalan number
In combinatorial mathematics, the Catalan numbers are a sequence of natural numbers that occur in various counting problems, often involving recursively defined objects. They are named after the French-Belgian mathematician Eugène Charles C ...
).
Traversal methods for ''m-''ary trees
Traversing a ''m''-ary tree is very similar to binary tree traversal. The pre-order traversal goes to parent, left subtree and the right subtree, and for traversing post-order it goes by left subtree, right subtree, and parent node. For traversing in-order, since there are more than two children per node for ''m > 2'', one must define the notion of ''left'' and ''right'' subtrees. One common method to establish left/right subtrees is to divide the list of children nodes into two groups. By defining an order on the ''m'' children of a node, the first nodes would constitute the left subtree and nodes would constitute the right subtree.Convert a ''m''-ary tree to binary tree
 Using an array for representing a ''m-''ary tree is inefficient, because most of the nodes in practical applications contain less than ''m'' children. As a result, this fact leads to a sparse array with large unused space in the memory. Converting an arbitrary ''m-''ary tree to a binary tree would only increase the height of the tree by a constant factor and would not affect the overall worst-case time complexity. In other words, since .
First, we link all the immediate children nodes of a given parent node together in order to form a link list. Then, we keep the link from the parent to the first (i.e., the leftmost) child and remove all the other links to the rest of the children. We repeat this process for all the children (if they have any children) until we have processed all the internal nodes and rotate the tree by 45 degrees clockwise. The tree obtained is the desired binary tree obtained from the given ''m''-ary tree.
Using an array for representing a ''m-''ary tree is inefficient, because most of the nodes in practical applications contain less than ''m'' children. As a result, this fact leads to a sparse array with large unused space in the memory. Converting an arbitrary ''m-''ary tree to a binary tree would only increase the height of the tree by a constant factor and would not affect the overall worst-case time complexity. In other words, since .
First, we link all the immediate children nodes of a given parent node together in order to form a link list. Then, we keep the link from the parent to the first (i.e., the leftmost) child and remove all the other links to the rest of the children. We repeat this process for all the children (if they have any children) until we have processed all the internal nodes and rotate the tree by 45 degrees clockwise. The tree obtained is the desired binary tree obtained from the given ''m''-ary tree.
Methods for storing ''m''-ary trees
Arrays
 ''m''-ary trees can also be stored in breadth-first order as an
''m''-ary trees can also be stored in breadth-first order as an implicit data structure In computer science, an implicit data structure or space-efficient data structure is a data structure that stores very little information other than the main or required data: a data structure that requires low overhead. They are called "implicit" ...
in array
An array is a systematic arrangement of similar objects, usually in rows and columns.
Things called an array include:
{{TOC right
Music
* In twelve-tone and serial composition, the presentation of simultaneous twelve-tone sets such that the ...
s, and if the tree is a complete ''m''-ary tree, this method wastes no space. In this compact arrangement, if a node has an index ''i'', its ''c''-th child in range is found at index , while its parent (if any) is found at index '''' (assuming the root has index zero, meaning a 0-based array). This method benefits from more compact storage and better locality of reference
In computer science, locality of reference, also known as the principle of locality, is the tendency of a processor to access the same set of memory locations repetitively over a short period of time. There are two basic types of reference localit ...
, particularly during a preorder traversal. The space complexity of this method is .
Pointer-based
Each node would have an internal array for storing pointers to each of its children: Compared to array-based implementation, this implementation method has superior space complexity of .
Compared to array-based implementation, this implementation method has superior space complexity of .
Enumeration of ''m-''ary trees
Listing all possible ''m''-ary trees are useful in many disciplines as a way of checking hypothesis or theories. Proper representation of ''m-''ary tree objects can greatly simplify the generation process. One can construct a ''bit sequence representation'' using the depth-first search of a ''m''-ary tree with ''n'' nodes indicating the presence of a node at a given index using binary values. For example, the bit sequence ''x=1110000100010001000'' is representing a 3-ary tree with ''n=6'' nodes as shown below. The problem with this representation is that listing all bit strings in lexicographic order would mean two successive strings might represent two trees that are lexicographically very different. Therefore, enumeration over binary strings would not necessarily result in an ordered generation of all ''m-''ary trees. A better representation is based on an integer string that indicates the number of zeroes between successive ones, known as ''Simple Zero Sequence''. is a Simple Zero Sequence corresponding to the bit sequence where ''j'' is the number of zeroes needed at the tail end of the sequence to make the string have the appropriate length. For example, is the simple zero sequence representation of the above figure. A more compact representation of ''00433'' is , which is called ''zero sequence'', which duplicate bases cannot be adjacent. This new representation allows to construct a next valid sequence in .
A simple zero sequence is valid if
That is to say that number of zeros in the bit sequence of a ''m''-ary tree cannot exceed the total number of null pointers (i.e., pointers without any child node attached to them). This summation is putting restriction on nodes so that there is room for adding the without creating an invalid structure (i.e. having an available null pointer to attached the last node to it).
The table below shows the list of all valid simple zero sequences of all ''3''-ary trees with 4 nodes:
Starting from the bottom right of the table (i.e., "000"), there is a ''backbone template'' that governs the generation of the possible ordered trees starting from "000" to "006". The backbone template for this group ("00X") is depicted below, where an additional node is added in the positions labeled "x".
The problem with this representation is that listing all bit strings in lexicographic order would mean two successive strings might represent two trees that are lexicographically very different. Therefore, enumeration over binary strings would not necessarily result in an ordered generation of all ''m-''ary trees. A better representation is based on an integer string that indicates the number of zeroes between successive ones, known as ''Simple Zero Sequence''. is a Simple Zero Sequence corresponding to the bit sequence where ''j'' is the number of zeroes needed at the tail end of the sequence to make the string have the appropriate length. For example, is the simple zero sequence representation of the above figure. A more compact representation of ''00433'' is , which is called ''zero sequence'', which duplicate bases cannot be adjacent. This new representation allows to construct a next valid sequence in .
A simple zero sequence is valid if
That is to say that number of zeros in the bit sequence of a ''m''-ary tree cannot exceed the total number of null pointers (i.e., pointers without any child node attached to them). This summation is putting restriction on nodes so that there is room for adding the without creating an invalid structure (i.e. having an available null pointer to attached the last node to it).
The table below shows the list of all valid simple zero sequences of all ''3''-ary trees with 4 nodes:
Starting from the bottom right of the table (i.e., "000"), there is a ''backbone template'' that governs the generation of the possible ordered trees starting from "000" to "006". The backbone template for this group ("00X") is depicted below, where an additional node is added in the positions labeled "x".
 Once one has exhausted all possible positions in the backbone template, a new template will be constructed by shifting the 3rd node one position to the right as depicted below, and the same enumeration would occur until all possible positions labeled "X" is exhausted.
Once one has exhausted all possible positions in the backbone template, a new template will be constructed by shifting the 3rd node one position to the right as depicted below, and the same enumeration would occur until all possible positions labeled "X" is exhausted.
 Going back to the table of enumeration of all ''m''-ary trees, where and , we can easily observe the apparent jump from "006" to "010" can be explained trivially in an algorithmic fashion as depicted below:
Going back to the table of enumeration of all ''m''-ary trees, where and , we can easily observe the apparent jump from "006" to "010" can be explained trivially in an algorithmic fashion as depicted below:
 The pseudocode for this enumeration is given below:
Procedure NEXT(''s''1, ''s''2, …, ''s''''n''−1)
if ''si'' = 0 for all ''i'' then
finished
else
''i'' ← max
''si'' ← ''si'' − 1
if ''i'' < ''n'' − 1 then
''si'' ← (''i'' + 1) ⋅ (''m'' − 1) − sum(''sj'')
end if
for ''j'' ← ''i'' + 2, ''i'' + 3, …, ''n'' − 1
''sj'' ← ''k'' − 1
end if
end
The pseudocode for this enumeration is given below:
Procedure NEXT(''s''1, ''s''2, …, ''s''''n''−1)
if ''si'' = 0 for all ''i'' then
finished
else
''i'' ← max
''si'' ← ''si'' − 1
if ''i'' < ''n'' − 1 then
''si'' ← (''i'' + 1) ⋅ (''m'' − 1) − sum(''sj'')
end if
for ''j'' ← ''i'' + 2, ''i'' + 3, …, ''n'' − 1
''sj'' ← ''k'' − 1
end if
end
Loopless enumeration
A generation algorithm that takes worst-case time are called loopless since the time complexity cannot involve a loop or recursion. Loopless enumeration of ''m-''ary trees is said to be loopless if after initialization, it generates successive tree objects in . For a given a ''m-''ary tree ''T'' with being one of its nodes and its -th child, a ''left-t rotation'' at is done by making the root node, and making and all of its subtrees a child of , additionally we assign the left most children of to and the right most child of stays attached to it while is promoted to root, as shown below: Convert an m-ary tree to left-tree
for ''i'' = 1...''n'':
for ''t'' = 2...''m'':
while ''t'' child of node at depth ''i'' ≠ 1:
L-t rotation at nodes at depth ''i''
end while
end for
end for
A ''right-t rotation'' at ''d'' is the inverse of this operation. The ''left chain'' of ''T'' is a sequence of nodes such that is the root and all nodes except have one child connected to their left most (i.e.,
Convert an m-ary tree to left-tree
for ''i'' = 1...''n'':
for ''t'' = 2...''m'':
while ''t'' child of node at depth ''i'' ≠ 1:
L-t rotation at nodes at depth ''i''
end while
end for
end for
A ''right-t rotation'' at ''d'' is the inverse of this operation. The ''left chain'' of ''T'' is a sequence of nodes such that is the root and all nodes except have one child connected to their left most (i.e.,