Lissajous Curve on:
[Wikipedia]
[Google]
[Amazon]
 A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of
A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of 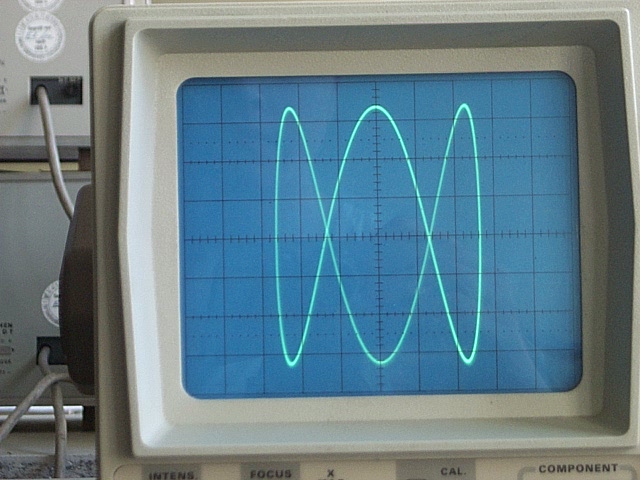 Lissajous figures where , ( is a
Lissajous figures where , ( is a
 The animation shows the curve adaptation with continuously increasing fraction from 0 to 1 in steps of 0.01 ().
Below are examples of Lissajous figures with an odd
The animation shows the curve adaptation with continuously increasing fraction from 0 to 1 in steps of 0.01 ().
Below are examples of Lissajous figures with an odd
File:Lissajous curve 1by2.svg, , , (1:2)
File:Lissajous curve 3by2.svg, , , (3:2)
File:Lissajous curve 3by4.svg, , , (3:4)
File:Lissajous curve 5by4.svg, , , (5:4)
File:Lissajous relaciones.png, alt=Lissajous figures: various frequency relations and phase differences , Lissajous figures: various frequency relations and phase differences
 When the input to an
When the input to an 
Lissajous Curve at Mathworld
from the NHMFL *
Physics applet
by Chiu-king Ng
Detailed Lissajous figures simulation
Drawing Lissajous figures with interactive sliders in Javascript
* ttp://jsxgraph.uni-bayreuth.de/wiki/index.php/Lissajous_curves Interactive Lissajous curve generator– Javascript applet using JSXGraph
Animated Lissajous figures
 A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of
A Lissajous curve , also known as Lissajous figure or Bowditch curve , is the graph of a system of parametric equation
In mathematics, a parametric equation defines a group of quantities as functions of one or more independent variables called parameters. Parametric equations are commonly used to express the coordinates of the points that make up a geometric ...
s
:
which describe the superposition of two perpendicular oscillations in x and y directions of different angular frequency (''a'' and ''b).'' The resulting family of curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
s was investigated by Nathaniel Bowditch
Nathaniel Bowditch (March 26, 1773 – March 16, 1838) was an early American mathematician remembered for his work on ocean navigation. He is often credited as the founder of modern maritime navigation; his book '' The New American Practical Navi ...
in 1815, and later in more detail in 1857 by Jules Antoine Lissajous (for whom it has been named). Such motions may be considered as a particular of kind of complex harmonic motion.
The appearance of the figure is sensitive to the ratio . For a ratio of 1, when the frequencies match a=b, the figure is an ellipse, with special cases including circles
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is cons ...
(, radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s) and lines
Line most often refers to:
* Line (geometry), object with zero thickness and curvature that stretches to infinity
* Telephone line, a single-user circuit on a telephone communication system
Line, lines, The Line, or LINE may also refer to:
Arts ...
(). A small change to one of the frequencies will mean the x oscillation after one cycle will be slightly out of synchronization with the y motion and so the ellipse will fail to close and trace a curve slightly adjacent during the next orbit showing as a precession of the ellipse. The pattern closes if the frequencies are whole number ratios i.e. is rational
Rationality is the quality of being guided by or based on reasons. In this regard, a person acts rationally if they have a good reason for what they do or a belief is rational if it is based on strong evidence. This quality can apply to an abil ...
.
Another simple Lissajous figure is the parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descri ...
(, ). Again a small shift of one frequency from the ratio 2 will result in the trace not closing but performing multiple loops successively shifted only closing if the ratio is rational as before. A complex dense pattern may form see below.
The visual form of such curves is often suggestive of a three-dimensional knot
A knot is an intentional complication in Rope, cordage which may be practical or decorative, or both. Practical knots are classified by function, including List of hitch knots, hitches, List of bend knots, bends, List of loop knots, loop knots, ...
, and indeed many kinds of knots, including those known as Lissajous knots, project to the plane as Lissajous figures.
Visually, the ratio determines the number of "lobes" of the figure. For example, a ratio of or produces a figure with three major lobes (see image). Similarly, a ratio of produces a figure with five horizontal lobes and four vertical lobes. Rational ratios produce closed (connected) or "still" figures, while irrational ratios produce figures that appear to rotate. The ratio determines the relative width-to-height ratio of the curve. For example, a ratio of produces a figure that is twice as wide as it is high. Finally, the value of determines the apparent "rotation" angle of the figure, viewed as if it were actually a three-dimensional curve. For example, produces and components that are exactly in phase, so the resulting figure appears as an apparent three-dimensional figure viewed from straight on (0°). In contrast, any non-zero produces a figure that appears to be rotated, either as a left–right or an up–down rotation (depending on the ratio ).
 Lissajous figures where , ( is a
Lissajous figures where , ( is a natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
) and
:
are Chebyshev polynomials
The Chebyshev polynomials are two sequences of polynomials related to the cosine and sine functions, notated as T_n(x) and U_n(x). They can be defined in several equivalent ways, one of which starts with trigonometric functions:
The Chebys ...
of the first kind of degree . This property is exploited to produce a set of points, called Padua points In polynomial interpolation of two variables, the Padua points are the first known example (and up to now the only one) of a unisolvent point set (that is, the interpolating polynomial is unique) with ''minimal growth'' of their Lebesgue constant, ...
, at which a function may be sampled in order to compute either a bivariate interpolation or quadrature of the function over the domain .
The relation of some Lissajous curves to Chebyshev polynomials is clearer to understand if the Lissajous curve which generates each of them is expressed using cosine functions rather than sine functions.
:
Examples
 The animation shows the curve adaptation with continuously increasing fraction from 0 to 1 in steps of 0.01 ().
Below are examples of Lissajous figures with an odd
The animation shows the curve adaptation with continuously increasing fraction from 0 to 1 in steps of 0.01 ().
Below are examples of Lissajous figures with an odd natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
, an even natural number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called '' cardinal ...
, and .
Generation
Prior to modern electronic equipment, Lissajous curves could be generated mechanically by means of a harmonograph.Practical application
Lissajous curves can also be generated using an oscilloscope (as illustrated). An octopus circuit can be used to demonstrate thewaveform
In electronics, acoustics, and related fields, the waveform of a signal is the shape of its graph as a function of time, independent of its time and magnitude scales and of any displacement in time.David Crecraft, David Gorham, ''Electron ...
images on an oscilloscope. Two phase-shifted sinusoid inputs are applied to the oscilloscope in X-Y mode and the phase relationship between the signals is presented as a Lissajous figure.
In the professional audio world, this method is used for realtime analysis of the phase relationship between the left and right channels of a stereo audio signal. On larger, more sophisticated audio mixing consoles an oscilloscope may be built-in for this purpose.
On an oscilloscope, we suppose is CH1 and is CH2, is the amplitude of CH1 and is the amplitude of CH2, is the frequency of CH1 and is the frequency of CH2, so is the ratio of frequencies of the two channels, and is the phase shift of CH1.
A purely mechanical application of a Lissajous curve with , is in the driving mechanism of the Mars Light type of oscillating beam lamps popular with railroads in the mid-1900s. The beam in some versions traces out a lopsided figure-8 pattern on its side.
Application for the case of
 When the input to an
When the input to an LTI system
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defin ...
is sinusoidal, the output is sinusoidal with the same frequency, but it may have a different amplitude and some phase shift
In physics and mathematics, the phase of a periodic function F of some real variable t (such as time) is an angle-like quantity representing the fraction of the cycle covered up to t. It is denoted \phi(t) and expressed in such a scale that it ...
. Using an oscilloscope that can plot one signal against another (as opposed to one signal against time) to plot the output of an LTI system against the input to the LTI system produces an ellipse that is a Lissajous figure for the special case of . The aspect ratio of the resulting ellipse is a function of the phase shift between the input and output, with an aspect ratio of 1 (perfect circle) corresponding to a phase shift of ±90° and an aspect ratio of ∞ (a line) corresponding to a phase shift of 0° or 180°.
The figure below summarizes how the Lissajous figure changes over different phase shifts. The phase shifts are all negative so that delay semantics
Semantics (from grc, σημαντικός ''sēmantikós'', "significant") is the study of reference, meaning, or truth. The term can be used to refer to subfields of several distinct disciplines, including philosophy, linguistics and compu ...
can be used with a causal
Causality (also referred to as causation, or cause and effect) is influence by which one event, process, state, or object (''a'' ''cause'') contributes to the production of another event, process, state, or object (an ''effect'') where the ca ...
LTI system (note that −270° is equivalent to +90°). The arrows show the direction of rotation of the Lissajous figure.
In engineering
A Lissajous curve is used in experimental tests to determine if a device may be properly categorized as amemristor
A memristor (; a portmanteau of ''memory resistor'') is a non-linear two-terminal electrical component relating electric charge and magnetic flux linkage. It was described and named in 1971 by Leon Chua, completing a theoretical quartet of ...
. It is also used to compare two different electrical signals: a known reference signal and a signal to be tested.
In popular culture
In motion pictures
*Lissajous figures were sometimes displayed on oscilloscopes meant to simulate high-tech equipment in science-fiction TV shows and movies in the 1960s and 1970s. *Thetitle sequence
A title sequence (also called an opening sequence or intro) is the method by which films or television programmes present their title and key production and cast members, utilizing conceptual visuals and sound (often a opening theme song with ...
by John Whitney for Alfred Hitchcock
Sir Alfred Joseph Hitchcock (13 August 1899 – 29 April 1980) was an English filmmaker. He is widely regarded as one of the most influential figures in the history of cinema. In a career spanning six decades, he directed over 50 featur ...
's 1958 feature film ''Vertigo
Vertigo is a condition where a person has the sensation of movement or of surrounding objects moving when they are not. Often it feels like a spinning or swaying movement. This may be associated with nausea, vomiting, sweating, or difficulties ...
'' is based on Lissajous figures.
Company logos
Lissajous figures are sometimes used in graphic design aslogo
A logo (abbreviation of logotype; ) is a graphic mark, emblem, or symbol used to aid and promote public identification and recognition. It may be of an abstract or figurative design or include the text of the name it represents as in a wordm ...
s. Examples include:
* The Australian Broadcasting Corporation
The Australian Broadcasting Corporation (ABC) is the national broadcaster of Australia. It is principally funded by direct grants from the Australian Government and is administered by a government-appointed board. The ABC is a publicly-own ...
(, , )
* The Lincoln Laboratory
The MIT Lincoln Laboratory, located in Lexington, Massachusetts, is a United States Department of Defense federally funded research and development center chartered to apply advanced technology to problems of national security. Research and de ...
at MIT
The Massachusetts Institute of Technology (MIT) is a private land-grant research university in Cambridge, Massachusetts. Established in 1861, MIT has played a key role in the development of modern technology and science, and is one of the ...
(, , )
* The University of Electro-Communications
The is a national university in the city of Chōfu, Tokyo, Japan.
It specialises in the disciplines of computer science, the physical sciences, engineering and technology. It was founded in 1918 as the Technical Institute for Wireless-Commu ...
, Japan (, , ).
* Disney's Movies Anywhere streaming video application uses a stylized version of the curve
* Facebook
Facebook is an online social media and social networking service owned by American company Meta Platforms. Founded in 2004 by Mark Zuckerberg with fellow Harvard College students and roommates Eduardo Saverin, Andrew McCollum, Dustin ...
's rebrand into Meta Platforms
Meta Platforms, Inc., (file no. 3835815) doing business as Meta and formerly named Facebook, Inc., and TheFacebook, Inc., is an American multinational technology conglomerate based in Menlo Park, California. The company owns Facebook, Instag ...
is also a Lissajous Curve, echoing the shape of a capital letter M (, , ).
In modern art
* TheDadaist
Dada () or Dadaism was an art movement of the European avant-garde in the early 20th century, with early centres in Zürich, Switzerland, at the Cabaret Voltaire (in 1916). New York Dada began c. 1915, and after 1920 Dada flourished in Par ...
artist Max Ernst
Max Ernst (2 April 1891 – 1 April 1976) was a German (naturalised American in 1948 and French in 1958) painter, sculptor, printmaker, graphic artist, and poet. A prolific artist, Ernst was a primary pioneer of the Dada movement and Surrealism ...
painted Lissajous figures directly by swinging a punctured bucket of paint over a canvas.
See also
*Lissajous orbit
In orbital mechanics, a Lissajous orbit (), named after Jules Antoine Lissajous, is a quasi-periodic orbital trajectory that an object can follow around a Lagrangian point of a three-body system without requiring any propulsion. Lyapunov orbi ...
* Blackburn pendulum
* Lemniscate of Gerono
* Spirograph
Spirograph is a geometric drawing device that produces mathematical roulette curves of the variety technically known as hypotrochoids and epitrochoids. The well-known toy version was developed by British engineer Denys Fisher and first sold ...
Notes
External links
Lissajous Curve at Mathworld
Interactive demos
* 3D Java applets depicting the construction of Lissajous curves in an oscilloscope: *from the NHMFL *
Physics applet
by Chiu-king Ng
Detailed Lissajous figures simulation
Drawing Lissajous figures with interactive sliders in Javascript
* ttp://jsxgraph.uni-bayreuth.de/wiki/index.php/Lissajous_curves Interactive Lissajous curve generator– Javascript applet using JSXGraph
Animated Lissajous figures
Wolfram Mathematica
Wolfram Mathematica is a software system with built-in libraries for several areas of technical computing that allow machine learning, statistics, symbolic computation, data manipulation, network analysis, time series analysis, NLP, optimiz ...
- Lissajous figures with interactive sliders in Wolfram mathematica
{{Authority control
Plane curves
Trigonometry
Articles containing video clips