Lifshitz Theory Of Van Der Waals Force

In condensed matter physics and physical chemistry, the Lifshitz theory of van der Waals forces, sometimes called the macroscopic theory of van der Waals forces, is a method proposed by Evgeny Mikhailovich Lifshitz in 1954 for treating van der Waals forces between bodies which does not assume pairwise additivity of the individual intermolecular forces; that is to say, the theory takes into account the influence of neighboring molecules on the interaction between every pair of molecules located in the two bodies, rather than treating each pair independently.

Need for a non-pairwise additive theory

The van der Waals force between two molecules, in this context, is the sum of the attractive or repulsive forces between them; these forces are primarily electrostatic in nature, and in their simplest form might consist of a force between two charges, two dipoles, or between a charge and a dipole. Thus, the strength of the force may often depend on the net charge, electric dipole moment, or the electric polarizability ($\alpha$) (see for example London force) of the molecules, with highly polarizable molecules contributing to stronger forces, and so on.

The total force between two bodies, each consisting of many molecules in the van der Waals theory is simply the sum of the intermolecular van der Waals forces, where pairwise additivity is assumed. That is to say, the forces are summed as though each pair of molecules interacts completely independently of their surroundings (See Van der Waals forces between Macroscopic Objects for an example of such a treatment). This assumption is usually correct for gasses, but presents a problem for many condensed materials, as it is known that the molecular interactions may depend strongly on their environment and neighbors. For example, in a conductor, a point-like charge might be screened by the electrons in the conductance band, and the polarizability of a condensed material may be vastly different from that of an individual molecule. In order to correctly predict the van der Waals forces of condensed materials, a theory that takes into account their total electrostatic response is needed.

General principle

The problem of pairwise additivity is completely avoided in the Lifshitz theory, where the molecular structure is ignored and the bodies are treated as continuous media. The forces between the bodies are now derived in terms of their bulk properties, such as dielectric constant and refractive index, which already contain all the necessary information from the original molecular structure.

The original Lifshitz 1955 paper proposed this method relying on quantum field theory principles, and is, in essence, a generalization of the Casimir effect, from two parallel, flat, ideally conducting surfaces, to two surfaces of any material. Later papers by Langbein, Ninham, Parsegian and Van Kampen showed that the essential equations could be derived using much simpler theoretical techniques, an example of which is presented here.

Hamaker constant

The Lifshitz theory can be expressed as an effective Hamaker constant in the van der Waals theory.

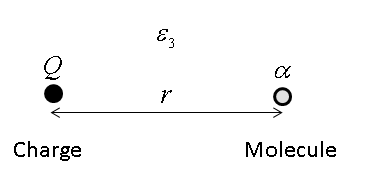
Consider, for example, the interaction between an ion of charge $Q$, and a nonpolar molecule with polarizability $\alpha_2$ at distance $r$. In a medium with dielectric constant $\epsilon_3$, the interaction energy between a charge and an electric dipole $p$ is given by
:$U(r)=\frac$

with the dipole moment of the polarizable molecule given by $p=\alpha_2 E$, where $E$ is the strength of the electric field at distance $r$ from the ion. According to Coulomb's law:
:$E = \frac \frac$

so we may write the interaction energy as

:$U(r)=\frac$


Consider now, how the interaction energy will change if the right hand molecule is replaced with a medium of density $\rho_2$ of such molecules. According to the "classical" van der Waals theory, the total force will simply be the summation over individual molecules. Integrating over the volume of the medium (see the third figure), we might expect the total interaction energy with the charge to be

:$\begin U(D)&= \frac \int \limits_^dz\int\limits_^dx \frac \\ & = -\frac \frac \end$

But this result cannot be correct, since It is well known that a charge $Q$ in a medium of dielectric constant $\epsilon_3$ at a distance $D$ from the plane surface of a second medium of dielectric constant $\epsilon_2$ experiences a force as if there were an 'image' charge of strength $Q'=-Q(\epsilon_2-\epsilon_3)/(\epsilon_2+\epsilon_3)$ at distance D on the other side of the boundary. The force between the real and image charges must then be

:$F(D)= \frac \frac$

and the energy, therefore

:$U(D) = \frac \frac$

Equating the two expressions for the energy, we define a new effective polarizability that must obey

:$\rho_2 \alpha_2 = \epsilon_0 \epsilon_3 \frac$

Similarly, replacing the real charge $Q$ with a medium of density $\rho_1$ and polarizability $\alpha_1$ gives an expression for $\alpha_1 \rho_1$. Using these two relations, we may restate our theory in terms of an effective Hamaker constant. Specifically, using McLachlan's generalized theory of VDW forces the Hamaker constant for an interaction potential of the form $U(r)=-C/r^n$ between two bodies at temperature $T$ is

:$A = \pi^2 C \rho_1 \rho_2 = \frac \sum_^\infty \frac$

with $\nu_n = 2\pi n k_B T / h$, where $k_B$ and $h$ are Boltzmann's and Planck's constants correspondingly. Inserting our relations for $\rho \alpha$ and approximating the sum as an integral $k_B T \sum_^\infty \rightarrow \frac\int\limits_^d\nu$, the effective Hamaker constant in the Lifshitz theory may be approximated as
:$A \approx \frac k_B T \left( \frac \right) \left( \frac \right) + \frac \int\limits_^ d\nu \left( \frac \right) \left( \frac \right)$

We note that $\epsilon(i\nu)$ are real functions, and are related to measurable properties of the medium; thus, the Hamaker constant in the Lifshitz theory can be expressed in terms of observable properties of the physical system.

Experimental validation

The macroscopic theory of van der Waals theory has many experimental validations. Among which, some of the most notable ones are Derjaguin (1960); Derjaguin, Abrikosova and Lifshitz (1956) and Israelachvili and Tabor (1973), who measured the balance of forces between macroscopic bodies of glass, or glass and mica; Haydon and Taylor (1968), who measured the forces across bilayers by measuring their contact angle; and lastly Shih and Parsegian (1975), who investigated Van der Waals potentials between heavy alkali-metal atoms and gold surfaces using atomic-beam-deflection.

References

{{Reflist

Physical chemistry
Condensed matter physics