Least-squares spectral analysis on:
[Wikipedia]
[Google]
[Amazon]
 Least-squares spectral analysis (LSSA) is a method of estimating a
Least-squares spectral analysis (LSSA) is a method of estimating a
 In the Vaníček method, a discrete data set is approximated by a weighted sum of sinusoids of progressively determined frequencies using a standard
In the Vaníček method, a discrete data set is approximated by a weighted sum of sinusoids of progressively determined frequencies using a standard
The frequencies are chosen using a method similar to Barning's, but going further in optimizing the choice of each successive new frequency by picking the frequency that minimizes the residual after least-squares fitting (equivalent to the fitting technique now known as matching pursuit with pre-backfitting). The number of sinusoids must be less than or equal to the number of data samples (counting sines and cosines of the same frequency as separate sinusoids). A data vector ''Φ'' is represented as a weighted sum of sinusoidal basis functions, tabulated in a matrix A by evaluating each function at the sample times, with weight vector ''x'': where the weights vector ''x'' is chosen to minimize the sum of squared errors in approximating ''Φ''. The solution for ''x'' is closed-form, using standard
 Trying to lower the computational burden of the Vaníček method in 1976 (no longer an issue), Lomb proposed using the above simplification in general, except for pair-wise correlations between sine and cosine bases of the same frequency, since the correlations between pairs of sinusoids are often small, at least when they are not tightly spaced. This formulation is essentially that of the traditional periodogram but adapted for use with unevenly spaced samples. The vector ''x'' is a reasonably good estimate of an underlying spectrum, but since we ignore any correlations, A''x'' is no longer a good approximation to the signal, and the method is no longer a least-squares method — yet in the literature continues to be referred to as such.
Rather than just taking dot products of the data with sine and cosine waveforms directly, Scargle modified the standard periodogram formula so to find a time delay first, such that this pair of sinusoids would be mutually orthogonal at sample times and also adjusted for the potentially unequal powers of these two basis functions, to obtain a better estimate of the power at a frequency. This procedure made his modified periodogram method exactly equivalent to Lomb's method. Time delay by definition equals to
Then the periodogram at frequency is estimated as:
which, as Scargle reports, has the same statistical distribution as the periodogram in the evenly sampled case.
At any individual frequency , this method gives the same power as does a least-squares fit to sinusoids of that frequency and of the form:
In practice, it is always difficult to judge if a given Lomb peak is significant or not, especially when the nature of the noise is unknown, so for example a false-alarm spectral peak in the Lomb periodogram analysis of noisy periodic signal may result from noise in turbulence data. Fourier methods can also report false spectral peaks when analyzing patched-up or data edited otherwise.
Trying to lower the computational burden of the Vaníček method in 1976 (no longer an issue), Lomb proposed using the above simplification in general, except for pair-wise correlations between sine and cosine bases of the same frequency, since the correlations between pairs of sinusoids are often small, at least when they are not tightly spaced. This formulation is essentially that of the traditional periodogram but adapted for use with unevenly spaced samples. The vector ''x'' is a reasonably good estimate of an underlying spectrum, but since we ignore any correlations, A''x'' is no longer a good approximation to the signal, and the method is no longer a least-squares method — yet in the literature continues to be referred to as such.
Rather than just taking dot products of the data with sine and cosine waveforms directly, Scargle modified the standard periodogram formula so to find a time delay first, such that this pair of sinusoids would be mutually orthogonal at sample times and also adjusted for the potentially unequal powers of these two basis functions, to obtain a better estimate of the power at a frequency. This procedure made his modified periodogram method exactly equivalent to Lomb's method. Time delay by definition equals to
Then the periodogram at frequency is estimated as:
which, as Scargle reports, has the same statistical distribution as the periodogram in the evenly sampled case.
At any individual frequency , this method gives the same power as does a least-squares fit to sinusoids of that frequency and of the form:
In practice, it is always difficult to judge if a given Lomb peak is significant or not, especially when the nature of the noise is unknown, so for example a false-alarm spectral peak in the Lomb periodogram analysis of noisy periodic signal may result from noise in turbulence data. Fourier methods can also report false spectral peaks when analyzing patched-up or data edited otherwise.
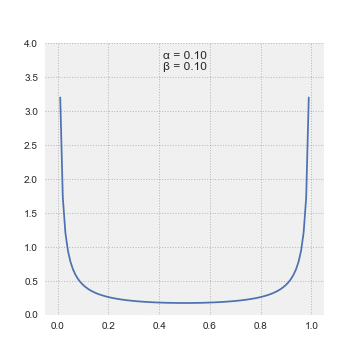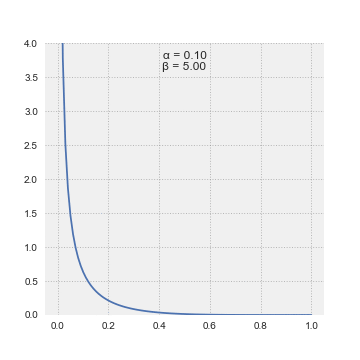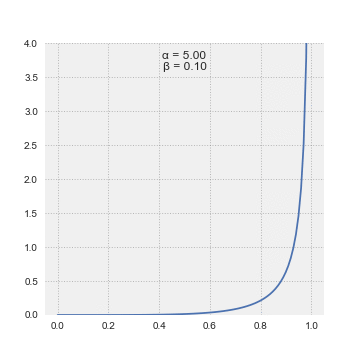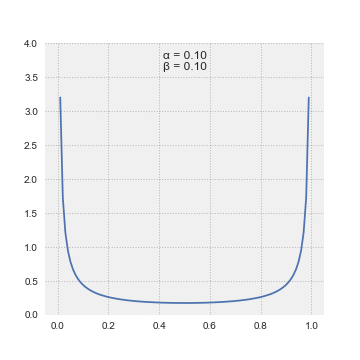 The most useful feature of LSSA is enabling incomplete records to be spectrally analyzed — without the need to manipulate data or to invent otherwise non-existent data.
Magnitudes in the LSSA
The most useful feature of LSSA is enabling incomplete records to be spectrally analyzed — without the need to manipulate data or to invent otherwise non-existent data.
Magnitudes in the LSSA
''The Least Squares Spectrum, Its Inverse Transform and Autocorrelation Function: Theory and Some Applications in Geodesy''
Ph.D. Dissertation, University of Toronto, Canada (1998). No such inverse procedure is known for the periodogram method.
LSSA package freeware download
FORTRAN, Vaníček's least-squares spectral analysis method, from the
LSWAVE package freeware download
MATLAB, includes the Vaníček's least-squares spectral analysis method, from the U.S. National Geodetic Survey. {{Authority control Algorithms Analysis of variance Applied mathematics Applied statistics Carl Friedrich Gauss Computational mathematics Computational science Data processing Digital signal processing Engineering statistics Frequency Frequency-domain analysis Harmonic analysis Iterative methods Least squares Linear algebra Mathematical analysis Mathematical optimization Mathematical physics Mathematics of computing Multivariate statistics Numerical analysis Numerical linear algebra Optimization algorithms and methods Signal processing Statistical forecasting Statistical methods Statistical signal processing Stochastic processes Theoretical computer science Time series
frequency spectrum
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed int ...
based on a least-squares fit of sinusoids to data samples, similar to Fourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fo ...
. Fourier analysis, the most used spectral method in science, generally boosts long-periodic noise in the long and gapped records; LSSA mitigates such problems. Unlike in Fourier analysis, data need not be equally spaced to use LSSA.
Developed in 1969 and 1971, LSSA is also known as the Vaníček method and the Gauss-Vaniček method after Petr Vaníček, and as the Lomb method or the Lomb–Scargle periodogram, based on the simplifications first by Nicholas R. Lomb and then by Jeffrey D. Scargle.
Historical background
The close connections betweenFourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fo ...
, the periodogram, and the least-squares fitting of sinusoids have been known for a long time.
However, most developments are restricted to complete data sets of equally spaced samples. In 1963, Freek J. M. Barning of Mathematisch Centrum, Amsterdam, handled unequally spaced data by similar techniques, including both a periodogram analysis equivalent to what nowadays is called the Lomb method and least-squares fitting of selected frequencies of sinusoids determined from such periodograms — and connected by a procedure known today as the matching pursuit with post-back fitting or the orthogonal matching pursuit.
Petr Vaníček, a Canadian geophysicist
Geophysics () is a subject of natural science concerned with the physical processes and properties of Earth and its surrounding space environment, and the use of quantitative methods for their analysis. Geophysicists conduct investigations acros ...
and geodesist of the University of New Brunswick
The University of New Brunswick (UNB) is a public university with two primary campuses in Fredericton and Saint John, New Brunswick. It is the oldest English language, English-language university in Canada, and among the oldest public universiti ...
, proposed in 1969 also the matching-pursuit approach for equally and unequally spaced data, which he called "successive spectral analysis" and the result a "least-squares periodogram". He generalized this method to account for any systematic components beyond a simple mean, such as a "predicted linear (quadratic, exponential, ...) secular trend of unknown magnitude", and applied it to a variety of samples, in 1971.
Vaníček's strictly least-squares method was then simplified in 1976 by Nicholas R. Lomb of the University of Sydney
The University of Sydney (USYD) is a public university, public research university in Sydney, Australia. Founded in 1850, it is the oldest university in both Australia and Oceania. One of Australia's six sandstone universities, it was one of the ...
, who pointed out its close connection to periodogram analysis. Subsequently, the definition of a periodogram of unequally spaced data was modified and analyzed by Jeffrey D. Scargle of NASA Ames Research Center, who showed that, with minor changes, it becomes identical to Lomb's least-squares formula for fitting individual sinusoid frequencies.
Scargle states that his paper "does not introduce a new detection technique, but instead studies the reliability and efficiency of detection with the most commonly used technique, the periodogram, in the case where the observation times are unevenly spaced," and further points out regarding least-squares fitting of sinusoids compared to periodogram analysis, that his paper "establishes, apparently for the first time, that (with the proposed modifications) these two methods are exactly equivalent."
Press summarizes the development this way:
In 1989, Michael J. Korenberg of Queen's University in Kingston, Ontario, developed the "fast orthogonal search" method of more quickly finding a near-optimal decomposition of spectra or other problems, similar to the technique that later became known as the orthogonal matching pursuit.
Development of LSSA and variants
The Vaníček method
linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
or least-squares fit.Wells, D.E., P. Vaníček, S. Pagiatakis, 1985. Least-squares spectral analysis revisited. Department of Surveying Engineering Technical Report 84, University of New Brunswick, Fredericton, 68 pages, Available aThe frequencies are chosen using a method similar to Barning's, but going further in optimizing the choice of each successive new frequency by picking the frequency that minimizes the residual after least-squares fitting (equivalent to the fitting technique now known as matching pursuit with pre-backfitting). The number of sinusoids must be less than or equal to the number of data samples (counting sines and cosines of the same frequency as separate sinusoids). A data vector ''Φ'' is represented as a weighted sum of sinusoidal basis functions, tabulated in a matrix A by evaluating each function at the sample times, with weight vector ''x'': where the weights vector ''x'' is chosen to minimize the sum of squared errors in approximating ''Φ''. The solution for ''x'' is closed-form, using standard
linear regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A mode ...
:
Here the matrix A can be based on any set of functions mutually independent (not necessarily orthogonal) when evaluated at the sample times; functions used for spectral analysis are typically sines and cosines evenly distributed over the frequency range of interest. If we choose too many frequencies in a too-narrow frequency range, the functions will be insufficiently independent, the matrix ill-conditioned, and the resulting spectrum meaningless.
When the basis functions in A are orthogonal (that is, not correlated, meaning the columns have zero pair-wise dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
s), the matrix ATA is diagonal; when the columns all have the same power (sum of squares of elements), then that matrix is an identity matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the obje ...
times a constant, so the inversion is trivial. The latter is the case when the sample times are equally spaced and sinusoids chosen as sines and cosines equally spaced in pairs on the frequency interval 0 to a half cycle per sample (spaced by 1/N cycles per sample, omitting the sine phases at 0 and maximum frequency where they are identically zero). This case is known as the discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
, slightly rewritten in terms of measurements and coefficients.
: — DFT case for ''N'' equally spaced samples and frequencies, within a scalar factor.
The Lomb method
The generalized Lomb–Scargle periodogram
The standard Lomb–Scargle periodogram is only valid for a model with a zero mean. Commonly, this is approximated — by subtracting the mean of the data before calculating the periodogram. However, this is an inaccurate assumption when the mean of the model (the fitted sinusoids) is non-zero. The ''generalized'' Lomb–Scargle periodogram removes this assumption and explicitly solves for the mean. In this case, the function fitted is The generalized Lomb–Scargle periodogram has also been referred to in the literature as a ''floating mean periodogram''.Korenberg's "fast orthogonal search" method
Michael Korenberg of Queen's University inKingston, Ontario
Kingston is a city in Ontario, Canada, on the northeastern end of Lake Ontario. It is at the beginning of the St. Lawrence River and at the mouth of the Cataraqui River, the south end of the Rideau Canal. Kingston is near the Thousand Islands, ...
, developed a method for choosing a sparse set of components from an over-complete set — such as sinusoidal components for spectral analysis — called the fast orthogonal search (FOS). Mathematically, FOS uses a slightly modified Cholesky decomposition in a mean-square error reduction (MSER) process, implemented as a sparse matrix
In numerical analysis and scientific computing, a sparse matrix or sparse array is a matrix in which most of the elements are zero. There is no strict definition regarding the proportion of zero-value elements for a matrix to qualify as sparse ...
inversion. As with the other LSSA methods, FOS avoids the major shortcoming of discrete Fourier analysis, so it can accurately identify embedded periodicities and excel with unequally spaced data. The fast orthogonal search method was also applied to other problems, such as nonlinear system identification System identification is a method of identifying or measuring the mathematical model of a system from measurements of the system inputs and outputs. The applications of system identification include any system where the inputs and outputs can be mea ...
.
Palmer's Chi-squared method
Palmer has developed a method for finding the best-fit function to any chosen number of harmonics, allowing more freedom to find non-sinusoidal harmonic functions. His is a fast ( FFT-based) technique for weighted least-squares analysis on arbitrarily spaced data with non-uniform standard errors. Source code that implements this technique is available. Because data are often not sampled at uniformly spaced discrete times, this method "grids" the data by sparsely filling a time series array at the sample times. All intervening grid points receive zero statistical weight, equivalent to having infinite error bars at times between samples.Applications
 The most useful feature of LSSA is enabling incomplete records to be spectrally analyzed — without the need to manipulate data or to invent otherwise non-existent data.
Magnitudes in the LSSA
The most useful feature of LSSA is enabling incomplete records to be spectrally analyzed — without the need to manipulate data or to invent otherwise non-existent data.
Magnitudes in the LSSA spectrum
A spectrum (: spectra or spectrums) is a set of related ideas, objects, or properties whose features overlap such that they blend to form a continuum. The word ''spectrum'' was first used scientifically in optics to describe the rainbow of co ...
depict the contribution of a frequency or period to the variance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
of the time series
In mathematics, a time series is a series of data points indexed (or listed or graphed) in time order. Most commonly, a time series is a sequence taken at successive equally spaced points in time. Thus it is a sequence of discrete-time data. ...
. Generally, spectral magnitudes thus defined enable the output's straightforward significance level regime.Beard, A.G., Williams, P.J.S., Mitchell, N.J. & Muller, H.G. A special climatology of planetary waves and tidal variability, J Atm. Solar-Ter. Phys. 63 (09), p.801–811 (2001). Alternatively, spectral magnitudes in the Vaníček spectrum can also be expressed in dB.Pagiatakis, S. Stochastic significance of peaks in the least-squares spectrum, J of Geodesy 73, p.67-78 (1999). Note that spectral magnitudes in the Vaníček spectrum follow β-distribution.
Inverse transformation of Vaníček's LSSA is possible, as is most easily seen by writing the forward transform as a matrix; the matrix inverse (when the matrix is not singular) or pseudo-inverse will then be an inverse transformation; the inverse will exactly match the original data if the chosen sinusoids are mutually independent at the sample points and their number is equal to the number of data points.Craymer, M.R.''The Least Squares Spectrum, Its Inverse Transform and Autocorrelation Function: Theory and Some Applications in Geodesy''
Ph.D. Dissertation, University of Toronto, Canada (1998). No such inverse procedure is known for the periodogram method.
Implementation
The LSSA can be implemented in less than a page ofMATLAB
MATLAB (an abbreviation of "MATrix LABoratory") is a proprietary multi-paradigm programming language and numeric computing environment developed by MathWorks. MATLAB allows matrix manipulations, plotting of functions and data, implementat ...
code. In essence:
"to compute the least-squares spectrum we must compute ''m'' spectral values ... which involves performing the least-squares approximation ''m'' times, each time to get he spectral powerfor a different frequency"I.e., for each frequency in a desired set of frequencies,
sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite th ...
and cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
functions are evaluated at the times corresponding to the data samples, and dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
s of the data vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
with the sinusoid vectors are taken and appropriately normalized; following the method known as Lomb/Scargle periodogram, a time shift is calculated for each frequency to orthogonalize the sine and cosine components before the dot product; finally, a power is computed from those two amplitude
The amplitude of a periodic variable is a measure of its change in a single period (such as time or spatial period). The amplitude of a non-periodic signal is its magnitude compared with a reference value. There are various definitions of am ...
components. This same process implements a discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
when the data are uniformly spaced in time and the frequencies chosen correspond to integer numbers of cycles over the finite data record.
This method treats each sinusoidal component independently, or out of context, even though they may not be orthogonal to data points; it is Vaníček's original method. In addition, it is possible to perform a full simultaneous or in-context least-squares fit by solving a matrix equation and partitioning the total data variance between the specified sinusoid frequencies. Such a matrix least-squares solution is natively available in MATLAB as the backslash
The backslash is a mark used mainly in computing and mathematics. It is the mirror image of the common slash (punctuation), slash . It is a relatively recent mark, first documented in the 1930s. It is sometimes called a hack, whack, Escape c ...
operator.
Furthermore, the simultaneous or in-context method, as opposed to the independent or out-of-context version (as well as the periodogram version due to Lomb), cannot fit more components (sines and cosines) than there are data samples, so that:
Lomb's periodogram method, on the other hand, can use an arbitrarily high number of, or density of, frequency components, as in a standard periodogram; that is, the frequency domain can be over-sampled by an arbitrary factor. However, as mentioned above, one should keep in mind that Lomb's simplification and diverging from the least squares criterion opened up his technique to grave sources of errors, resulting even in false spectral peaks.
In Fourier analysis, such as the Fourier transform
In mathematics, the Fourier transform (FT) is an integral transform that takes a function as input then outputs another function that describes the extent to which various frequencies are present in the original function. The output of the tr ...
and discrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
, the sinusoids fitted to data are all mutually orthogonal, so there is no distinction between the simple out-of-context dot-product-based projection onto basis functions versus an in-context simultaneous least-squares fit; that is, no matrix inversion is required to least-squares partition the variance between orthogonal sinusoids of different frequencies. In the past, Fourier's was for many a method of choice thanks to its processing-efficient fast Fourier transform
A fast Fourier transform (FFT) is an algorithm that computes the discrete Fourier transform (DFT) of a sequence, or its inverse (IDFT). A Fourier transform converts a signal from its original domain (often time or space) to a representation in ...
implementation when complete data records with equally spaced samples are available, and they used the Fourier family of techniques to analyze gapped records as well, which, however, required manipulating and even inventing non-existent data just so to be able to run a Fourier-based algorithm.
See also
* Non-uniform discrete Fourier transform *Orthogonal functions
In mathematics, orthogonal functions belong to a function space that is a vector space equipped with a bilinear form. When the function space has an interval (mathematics), interval as the domain of a function, domain, the bilinear form may be the ...
* SigSpec
* Sinusoidal model
* Spectral density
In signal processing, the power spectrum S_(f) of a continuous time signal x(t) describes the distribution of power into frequency components f composing that signal. According to Fourier analysis, any physical signal can be decomposed into ...
* Spectral density estimation, for competing alternatives
References
External links
LSSA package freeware download
FORTRAN, Vaníček's least-squares spectral analysis method, from the
University of New Brunswick
The University of New Brunswick (UNB) is a public university with two primary campuses in Fredericton and Saint John, New Brunswick. It is the oldest English language, English-language university in Canada, and among the oldest public universiti ...
.
LSWAVE package freeware download
MATLAB, includes the Vaníček's least-squares spectral analysis method, from the U.S. National Geodetic Survey. {{Authority control Algorithms Analysis of variance Applied mathematics Applied statistics Carl Friedrich Gauss Computational mathematics Computational science Data processing Digital signal processing Engineering statistics Frequency Frequency-domain analysis Harmonic analysis Iterative methods Least squares Linear algebra Mathematical analysis Mathematical optimization Mathematical physics Mathematics of computing Multivariate statistics Numerical analysis Numerical linear algebra Optimization algorithms and methods Signal processing Statistical forecasting Statistical methods Statistical signal processing Stochastic processes Theoretical computer science Time series