kissing number problem on:
[Wikipedia]
[Google]
[Amazon]
In

 Proof: Consider a circle with center ''C'' that is touched by circles with centers ''C''1, ''C''2, .... Consider the rays ''C'' ''C''''i''. These rays all emanate from the same center ''C'', so the sum of angles between adjacent rays is 360°.
Assume by contradiction that there are more than six touching circles. Then at least two adjacent rays, say ''C'' ''C''1 and ''C'' ''C''2, are separated by an angle of less than 60°. The segments ''C Ci'' have the same length – 2''r'' – for all ''i''. Therefore, the triangle ''C'' ''C''1 ''C''2 is
Proof: Consider a circle with center ''C'' that is touched by circles with centers ''C''1, ''C''2, .... Consider the rays ''C'' ''C''''i''. These rays all emanate from the same center ''C'', so the sum of angles between adjacent rays is 360°.
Assume by contradiction that there are more than six touching circles. Then at least two adjacent rays, say ''C'' ''C''1 and ''C'' ''C''2, are separated by an angle of less than 60°. The segments ''C Ci'' have the same length – 2''r'' – for all ''i''. Therefore, the triangle ''C'' ''C''1 ''C''2 is 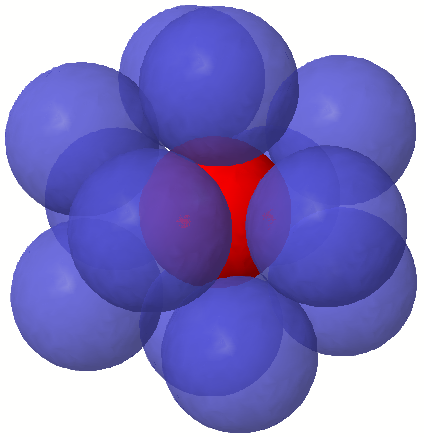

Table of the Highest Kissing Numbers Presently Known
maintained by Gabriele Nebe and
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, the kissing number of a mathematical space
In mathematics, a space is a set (sometimes known as a ''universe'') endowed with a structure defining the relationships among the elements of the set.
A subspace is a subset of the parent space which retains the same structure.
While modern ma ...
is defined as the greatest number of non-overlapping unit sphere
A sphere (from Ancient Greek, Greek , ) is a surface (mathematics), surface analogous to the circle, a curve. In solid geometry, a sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
s that can be arranged in that space such that they each touch a common unit sphere. For a given sphere packing
In geometry, a sphere packing is an arrangement of non-overlapping spheres within a containing space. The spheres considered are usually all of identical size, and the space is usually three-dimensional Euclidean space. However, sphere packing p ...
(arrangement of spheres) in a given space, a kissing number can also be defined for each individual sphere as the number of spheres it touches. For a lattice packing the kissing number is the same for every sphere, but for an arbitrary sphere packing the kissing number may vary from one sphere to another.
Other names for kissing number that have been used are Newton number (after the originator of the problem), and contact number.
In general, the kissing number problem seeks the maximum possible kissing number for ''n''-dimensional spheres in (''n'' + 1)-dimensional Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
. Ordinary spheres correspond to two-dimensional closed surfaces in three-dimensional space.
Finding the kissing number when centers of spheres are confined to a line (the one-dimensional case) or a plane (two-dimensional case) is trivial. Proving a solution to the three-dimensional case, despite being easy to conceptualise and model in the physical world, eluded mathematicians until the mid-20th century. Solutions in higher dimensions are considerably more challenging, and only a handful of cases have been solved exactly. For others, investigations have determined upper and lower bounds, but not exact solutions.
Known greatest kissing numbers
One dimension
In one dimension, the kissing number is 2:Two dimensions
In two dimensions, the kissing number is 6:isosceles
In geometry, an isosceles triangle () is a triangle that has two sides of equal length and two angles of equal measure. Sometimes it is specified as having ''exactly'' two sides of equal length, and sometimes as having ''at least'' two sides ...
, and its third side – ''C''1 ''C''2 – has a side length of less than 2''r''. Therefore, the circles 1 and 2 intersect – a contradiction.

Three dimensions
In three dimensions, the kissing number is 12, but the correct value was much more difficult to establish than in dimensions one and two. It is easy to arrange 12 spheres so that each touches a central sphere, with a lot of space left over, and it is not obvious that there is no way to pack in a 13th sphere. (In fact, there is so much extra space that any two of the 12 outer spheres can exchange places through a continuous movement without any of the outer spheres losing contact with the center one.) This was the subject of a famous disagreement between mathematiciansIsaac Newton
Sir Isaac Newton () was an English polymath active as a mathematician, physicist, astronomer, alchemist, theologian, and author. Newton was a key figure in the Scientific Revolution and the Age of Enlightenment, Enlightenment that followed ...
and David Gregory. Newton correctly thought that the limit was 12; Gregory thought that a 13th could fit. Some incomplete proofs that Newton was correct were offered in the nineteenth century, most notably one by Reinhold Hoppe, but the first correct proof (according to Brass, Moser, and Pach) did not appear until 1953.
The twelve neighbors of the central sphere correspond to the maximum bulk coordination number
In chemistry, crystallography, and materials science, the coordination number, also called ligancy, of a central atom in a molecule or crystal is the number of atoms, molecules or ions bonded to it. The ion/molecule/atom surrounding the central ion ...
of an atom in a crystal lattice
In crystallography, crystal structure is a description of ordered arrangement of atoms, ions, or molecules in a crystal, crystalline material. Ordered structures occur from intrinsic nature of constituent particles to form symmetric patterns that ...
in which all atoms have the same size (as in a chemical element). A coordination number of 12 is found in a cubic close-packed
In geometry, close-packing of equal spheres is a dense arrangement of congruent spheres in an infinite, regular arrangement (or lattice). Carl Friedrich Gauss proved that the highest average density – that is, the greatest fraction of space occ ...
or a hexagonal close-packed structure.
Larger dimensions
In four dimensions, the kissing number is 24. This was proven in 2003 by Oleg Musin. Previously, the answer was thought to be either 24 or 25: it is straightforward to produce a packing of 24 spheres around a central sphere (one can place the spheres at the vertices of a suitably scaled24-cell
In four-dimensional space, four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octa ...
centered at the origin), but, as in the three-dimensional case, there is a lot of space left over — even more, in fact, than for ''n'' = 3 — so the situation was even less clear.
The existence of the highly symmetrical ''E''8 lattice and Leech lattice
In mathematics, the Leech lattice is an even unimodular lattice Λ24 in 24-dimensional Euclidean space which is one of the best models for the kissing number problem. It was discovered by . It may also have been discovered (but not published) by Er ...
has allowed known results for ''n'' = 8 (where the kissing number is 240), and ''n'' = 24 (where it is 196,560).
The kissing number in ''n'' dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
s is unknown for other dimensions.
If arrangements are restricted to ''lattice'' arrangements, in which the centres of the spheres all lie on points in a lattice, then this restricted kissing number is known for ''n'' = 1 to 9 and ''n'' = 24 dimensions. For 5, 6, and 7 dimensions the arrangement with the highest known kissing number found so far is the optimal lattice arrangement, but the existence of a non-lattice arrangement with a higher kissing number has not been excluded.
Some known bounds
The following table lists some known bounds on the kissing number in various dimensions. The dimensions in which the kissing number is known are listed in boldface.Generalization
The kissing number problem can be generalized to the problem of finding the maximum number of non-overlappingcongruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In modu ...
copies of any convex body
In mathematics, a convex body in n-dimensional Euclidean space \R^n is a compact convex set with non- empty interior. Some authors do not require a non-empty interior, merely that the set is non-empty.
A convex body K is called symmetric if it ...
that touch a given copy of the body. There are different versions of the problem depending on whether the copies are only required to be congruent to the original body, translates
Translation is the communication of the semantics, meaning of a #Source and target languages, source-language text by means of an Dynamic and formal equivalence, equivalent #Source and target languages, target-language text. The English la ...
of the original body, or translated by a lattice. For the regular tetrahedron
In geometry, a tetrahedron (: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular Face (geometry), faces, six straight Edge (geometry), edges, and four vertex (geometry), vertices. The tet ...
, for example, it is known that both the lattice kissing number and the translative kissing number are equal to 18, whereas the congruent kissing number is at least 56.
Algorithms
There are severalapproximation algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned sol ...
s on intersection graphs where the approximation ratio depends on the kissing number. For example, there is
a polynomial-time 10-approximation algorithm to find a maximum non-intersecting subset of a set of rotated unit squares.
Mathematical statement
The kissing number problem can be stated as the existence of a solution to a set of inequalities. Let be a set of ''N'' ''D''-dimensional position vectors of the centres of the spheres. The condition that this set of spheres can lie round the centre sphere without overlapping is: Thus the problem for each dimension can be expressed in the existential theory of the reals. However, general methods of solving problems in this form take at leastexponential time
In theoretical computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations p ...
which is why this problem has only been solved up to four dimensions. By adding additional variables, this can be converted to a single quartic equation
In mathematics, a quartic equation is one which can be expressed as a ''quartic function'' equaling zero. The general form of a quartic equation is
:ax^4+bx^3+cx^2+dx+e=0 \,
where ''a'' ≠ 0.
The quartic is the highest order polynom ...
in ''N''(''N'' − 1)/2 + ''DN'' variables:Concerning the matrix only the entries having ''m'' < ''n'' are needed. Or, equivalent, the matrix can be assumed to be antisymmetric. Anyway the matrix has just''N''(''N'' − 1)/2 free scalar variables. In addition, there are ''N'' ''D''-dimensional vectors ''x''''n'', which correspondent to a matrix of ''N'' column vectors.
Therefore, to solve the case in ''D'' = 5 dimensions and ''N'' = 40 + 1 vectors would be equivalent to determining the existence of real solutions to a quartic polynomial in 1025 variables. For the ''D'' = 24 dimensions and ''N'' = 196560 + 1, the quartic would have 19,322,732,544 variables. An alternative statement in terms of distance geometry is given by the distances squared between the ''m''th and ''n''th sphere:
This must be supplemented with the condition that the Cayley–Menger determinant
In linear algebra, geometry, and trigonometry, the Cayley–Menger determinant is a formula for the content, i.e. the higher-dimensional volume, of a n-dimensional simplex in terms of the squares of all of the distances between pairs of its ...
is zero for any set of points which forms a (''D'' + 1) simplex in ''D'' dimensions, since that volume must be zero. Setting gives a set of simultaneous polynomial equations in just ''y'' which must be solved for real values only. The two methods, being entirely equivalent, have various different uses. For example, in the second case one can randomly alter the values of the ''y'' by small amounts to try to minimise the polynomial in terms of the ''y''.
See also
* Equilateral dimension * Spherical code * Soddy's hexlet * Cylinder sphere packingNotes
References
* * T. Aste and D. Weaire '' The Pursuit of Perfect Packing'' (Institute Of Physics Publishing London 2000)Table of the Highest Kissing Numbers Presently Known
maintained by Gabriele Nebe and
Neil Sloane
__NOTOC__
Neil James Alexander Sloane FLSW (born October 10, 1939) is a British-American mathematician. His major contributions are in the fields of combinatorics, error-correcting codes, and sphere packing. Sloane is best known for being the cre ...
(lower bounds)
*
External links
* {{Packing problem Discrete geometry Packing problems