Kicked Rotor

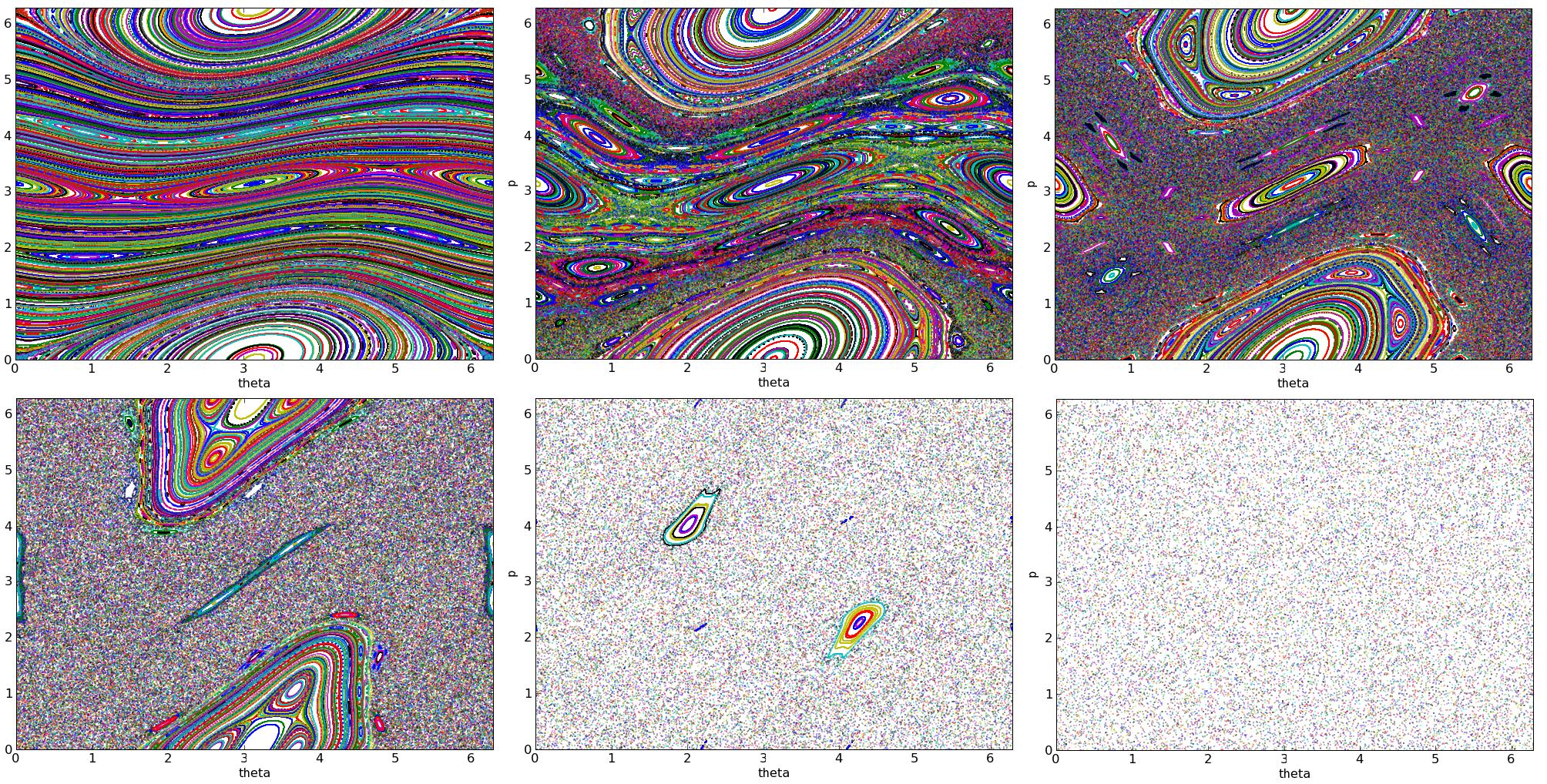
The kicked rotator, also spelled as kicked rotor, is a paradigmatic model for both Hamiltonian chaos (the study of chaos in Hamiltonian systems) and quantum chaos. It describes a free rotating stick (with moment of inertia $I$) in an inhomogeneous "gravitation like" field that is periodically switched on in short pulses. The model is described by the Hamiltonian

: $\mathcal(\theta,p,t)= \frac + K \cos \theta \sum_^\infty \delta \left(\frac-n\right)$,

where \theta \in conjugated_momentum_of_$\theta$,_$_\textstyle_K_$_is_the_kicking_strength,_$T$_is_the_kicking_period_and_$_\textstyle_\delta_$_is_the_Dirac_delta.html" ;"title="/math> is the angular position of the stick ($\theta=\pi$ corresponds to the position of the rotator at rest), $p$ is the Hamiltonian mechanics">conjugated momentum of $\theta$, $\textstyle K$ is the kicking strength, $T$ is the kicking period and $\textstyle \delta$ is the Dirac delta">Dirac delta function.

Classical properties

Stroboscopic dynamics

The equations of motion of the kicked rotator write$\frac = \frac = \frac \quad \text \quad \frac = -\frac = K \sin \theta \sum_^\infty \delta \left(\frac-n\right)$Theses equations show that between two consecutive kicks, the rotator simply moves freely: the momentum $p$ is conserved and the angular position growths linearly in time. On the other hand, during each kick the momentum abruptly jumps by a quantity $K T \sin \theta$, where $\theta$ is the angular position near the kick. The kicked rotator dynamics can thus be described by the discrete map$p_=p_n+ KT \sin \theta_n \quad \text \quad \theta_ = \theta_n + \frac p_$where $\theta_n$ and $p_n$ are the canonical coordinates at time $t=nT^-$, just before the $n$-th kick. It is usually more convenient to introduce dimensionless momentum $p \rightarrow p/\frac$, time $t \rightarrow t/T$ and kicking strength $K \rightarrow K/\frac$ to reduce the dynamics to the single parameter map$p_=p_n+ K \sin \theta_n \quad \text \quad \theta_ = \theta_n + p_$known as Chirikov standard map, with the caveat that $p_n$is not periodic as in the standard map. However, one can directly see that two rotators with same initial angular position $\theta_0$ but shifted dimensionless momentum $p_0$ and $p_0+ 2\pi l$ (with $l$ an arbitrary integer) will have the same exact stroboscopic dynamics, but with dimensionless momentum shifted at any time by $2\pi l$ (this is why stroboscopic phase portraits of the kicked rotator are usually displayed in a single momentum cell p \in \pi ,\pi/math>).

Transition from integrability to chaos

The kicked rotator is a prototype model to illustrate the transition from integrability to chaos in Hamiltonian systems and in particular the Kolmogorov–Arnold–Moser theorem. In the limit $K=0$, the system describes the free motion of the rotator, the momentum is conserved (the system is integrable) and the corresponding trajectories are straight lines in the $(\theta,p)$ plane (phase space), that is tori. For small, but non-vanishing perturbation $K$, instabilities and chaos starts to develop. Only quasi-periodic orbits (represented by invariant tori in phase space) remain stables, while other orbits become unstables. For larger $K$, invariant tori are eventually destroyed by the perturbation. For the value $K=K_c\approx0.971635\dots$, the last invariant tori connecting $\theta=-\pi$ and $\theta= \pi$ in phase space is destroyed.

Diffusion in momentum direction

For $K>K_c$, chaotic unstable orbits are no longer constraints by invariant tori in the momentum direction and can explore the full phase space. For $K \gg K_c$, the particle after each kicks typically moved over a large distance, which strongly modifies the amplitude and sign of the following kick. At long time enough, the particle as thus been submitted to a series of kicks with quasi-random amplitudes. This quasi-random walk is responsible for a diffusion process in the momentum direction $\langle (\Delta p_n)^2 \rangle = 2 D_\text n$ (where the average runs over different initial conditions).

More precisely, after $n$ kicks, the momentum $p_n$ of a particle with initial momentum $p_0$ writes $p_n = p_0 + K\sum_^\sin \theta_i$ (obtained by iterating $n$ times the standard map). Assuming that kicks are randoms and uncorrelated in time, the spreading of the momentum distribution writes$\left \langle ^ \right \rangle = \left \langle ^ \right \rangle = K^2\sum_^\left \langle ^ \theta_i \right \rangle + K^2 \sum_^\left \langle \sin \theta_i \sin \theta_j \right \rangle \approx K^2\sum_^\left \langle ^ \theta_i \right \rangle = \frac K n$The classical diffusion coefficient in momentum direction is then given in first approximation by $D_\text = \frac$. Corrections coming from neglected correlation terms can actually be taken into account, leading to the improved expression D_\text = \frac -2J_2(K)+2J_2^2(K)where $J_2$ is the Bessel function of first kind.

The quantum kicked rotator

Stroboscopic dynamics

The dynamics of the quantum kicked rotator (with wave function $, \psi(t) \rangle$) is governed by the time dependent Schrödinger's equation

: i\hbar\frac, \psi(t) \rangle=\left frac + K \cos \hat \sum_^\infty \delta \left(\frac-n \right)\right \psi(t) \rangle

with \hat,\hati\hbar (or equivalently $\langle \theta , \hat , \psi \rangle= i\hbar \frac$).

As for classical dynamics, a stroboscopic point of view can be adopted by introducing the time propagator over a kicking period $\hat$ (that is the Floquet operator) so that $, \psi(t+T) \rangle = \hat , \psi(t) \rangle$. After a careful integration of the time-dependent Schrödinger's equation, one finds that $\hat$ can be written as the product of two operators\hat=\exp\left i\frac\right\exp\left i\frac \cos\hat\right/math>We recover the classical interpretation: the dynamics of the quantum kicked rotor between two kicks is the succession of a free propagation during a time $T$ followed by a short kick. This simple expression of the Floquet operator $\hat$ (a product of two operators, one diagonal in momentum basis, the other one diagonal in angular position basis) allows to easily numerically solve the evolution of a given wave function using split-step method.

Because of the periodic boundary conditions at $\theta=\pm \pi$, any wave function $, \psi \rangle$ can be expanded in a discrete momentum basis $, l \rangle$ (with $p=l \hbar$, $l$ integer) see Bloch theorem), so that

: $\langle \theta , \psi \rangle =\sum_^ \langle l , \psi \rangle \mathrm^ \Leftrightarrow \langle l , \psi \rangle = \int_^ \frac \langle \theta , \psi \rangle \mathrm^$

Using this relation with the above expression of $\hat$, we find the recursion relation$\langle l, \psi(t+T) \rangle = \exp\left(-i\frac\right) \sum_^\infty (-i)^ J_ \left(\frac \right) \langle m, \psi(t) \rangle$where $\textstyle _n$ is a Bessel function of first kind.

Dynamical localization

It has been discoveredG. Casati, B.V. Chirikov, F.M. Izrailev and J. Ford,
in ''Stochastic Behaviour in classical and Quantum Hamiltonian Systems'', Vol. 93 of Lecture Notes in Physics, edited by G. Casati and J. Ford (Springer, N.Y. 1979), p. 334 that the classical diffusion is suppressed in the quantum kicked rotator. It was later understood that this is a manifestation of a quantum dynamical localization effect that parallels Anderson localization. There is a general argument that leads to the following estimate for the breaktime of the diffusive behavior

: $t^* \ \approx \ D_/\hbar^2$

Where $D_$ is the classical diffusion coefficient. The associated localization scale in momentum is therefore $\textstyle \sqrt$.

Link with Anderson tight-binding model

The quantum kicked rotor can actually formally be related to the Anderson tight-binding model a celebrated Hamiltonian that describes electrons in a disordered lattice with lattice site state $, n \rangle$, where Anderson localization takes place (in one dimension)$\hat = \sum_ \varepsilon_n , n \rangle \langle n, + \sum_ t_ , n \rangle \langle m ,$where the $\varepsilon_n$ are random on-site energies, and the $t_$ are the hoping amplitudes between sites $n$ and $m$.

In the quantum kicked rotator it can be shown, that the plane wave $, p \rangle$ with quantized momentum $p = n \hbar$ play the role of the lattice sites states. The full mapping to the Anderson tight-binding model goes as follow (for a given eigenstates of the Floquet operator, with quasi-energy $\omega$) t_n = - \int_^ \frac \tan \cos(x)/2\mathrm^ \quad \text \quad \varepsilon_n = \tan(\omega/2 - n^2/4)Dynamical localization in the quantum kicked rotator then actually takes place in the momentum basis.

The effect of noise and dissipation

If noise is added to the system, the dynamical localization is destroyed, and diffusion is induced. This is somewhat similar to hopping conductance.
The proper analysis requires to figure out how the dynamical correlations that are responsible for the localization effect are diminished.

Recall that the diffusion coefficient is $D_\approx K^2/2$, because the change $(p(t)-p(0))$ in the momentum is the sum of quasi-random kicks $K\sin(x(n))$. An exact expression for $D_$ is obtained by calculating the "area" of the correlation function $C(n) = \langle \sin(x(n))\sin(x(0)) \rangle$, namely the sum $D = K^2\sum C(n)$. Note that $C(0)=1/2$. The same calculation recipe holds also in the quantum mechanical case, and also if noise is added.

In the quantum case, without the noise, the ''area'' under $C(n)$ is zero (due to long negative tails), while with the noise a practical approximation is $C(n)\mapsto C(n) e^$ where the coherence time $t_c$ is inversely proportional to the intensity of the noise. Consequently, the noise induced diffusion coefficient is

: D \approx D_t^* / t_c \quad
textt_c \gg t^*

Also the problem of quantum kicked rotator with dissipation (due to coupling to a thermal bath) has been considered. There is an issue here how to introduce an interaction that respects the angle periodicity of the position $x$ coordinate, and is still spatially homogeneous. In the first works
a quantum-optic type interaction has been assumed that involves a momentum dependent coupling. Later a way to formulate a purely position dependent coupling, as in the Calderia-Leggett model, has been figured out, which can be regarded as the earlier version of the DLD model.

Experimental realization with cold atoms

The first experimental realizations of the quantum kicked rotator have been achieved by Mark G. Raizen group in 1995, later followed by the Auckland group, and have encouraged a renewed interest in the theoretical analysis. In this kind of experiment, a sample of cold atoms provided by a magneto-optical trap interacts with a pulsed standing wave of light. The light being detuned with respect to the atomic transitions, atoms undergo a space-periodic conservative force. Hence, the angular dependence is replaced by a dependence on position in the experimental approach. Sub-milliKelvin cooling is necessary to obtain quantum effects: because of the Heisenberg uncertainty principle, the de Broglie wavelength, i.e. the atomic wavelength, can become comparable to the light wavelength. For further information, see.M. Raizen in ''New directions in quantum chaos'', Proceedings of the International School of Physics ''Enrico Fermi'', Course CXLIII, Edited by G. Casati, I. Guarneri and U. Smilansky (IOS Press, Amsterdam 2000).
Thanks to this technique, several phenomena have been investigated, including the noticeable:
* quantum Ratchets;
* the Anderson transition in 3D.

See also

* Circle map

References

External links

Scholarpedia entry

{{Chaos theory

Quantum mechanics
Articles containing video clips
Chaotic maps