|
Floquet Theory
Floquet theory is a branch of the theory of ordinary differential equations relating to the class of solutions to periodic linear differential equations of the form :\dot = A(t) x, with \displaystyle A(t) a piecewise continuous periodic function with period T and defines the state of the stability of solutions. The main theorem of Floquet theory, Floquet's theorem, due to , gives a canonical form for each fundamental matrix solution of this common linear system. It gives a coordinate change \displaystyle y=Q^(t)x with \displaystyle Q(t+2T)=Q(t) that transforms the periodic system to a traditional linear system with constant, real coefficients. When applied to physical systems with periodic potentials, such as crystals in condensed matter physics, the result is known as Bloch's theorem. Note that the solutions of the linear differential equation form a vector space. A matrix \phi\,(t) is called a '' fundamental matrix solution'' if all columns are linearly independent solution ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Ordinary Differential Equations
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast with the term partial differential equation which may be with respect to ''more than'' one independent variable. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where , ..., and are arbitrary differentiable functions that do not need to be linear, and are the successive derivatives of the unknown function of the variable . Among ordinary differential equations, linear differential equations play a prominent role for several reasons. Most elementary and special functions that are encountered in physics and applied mathemati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
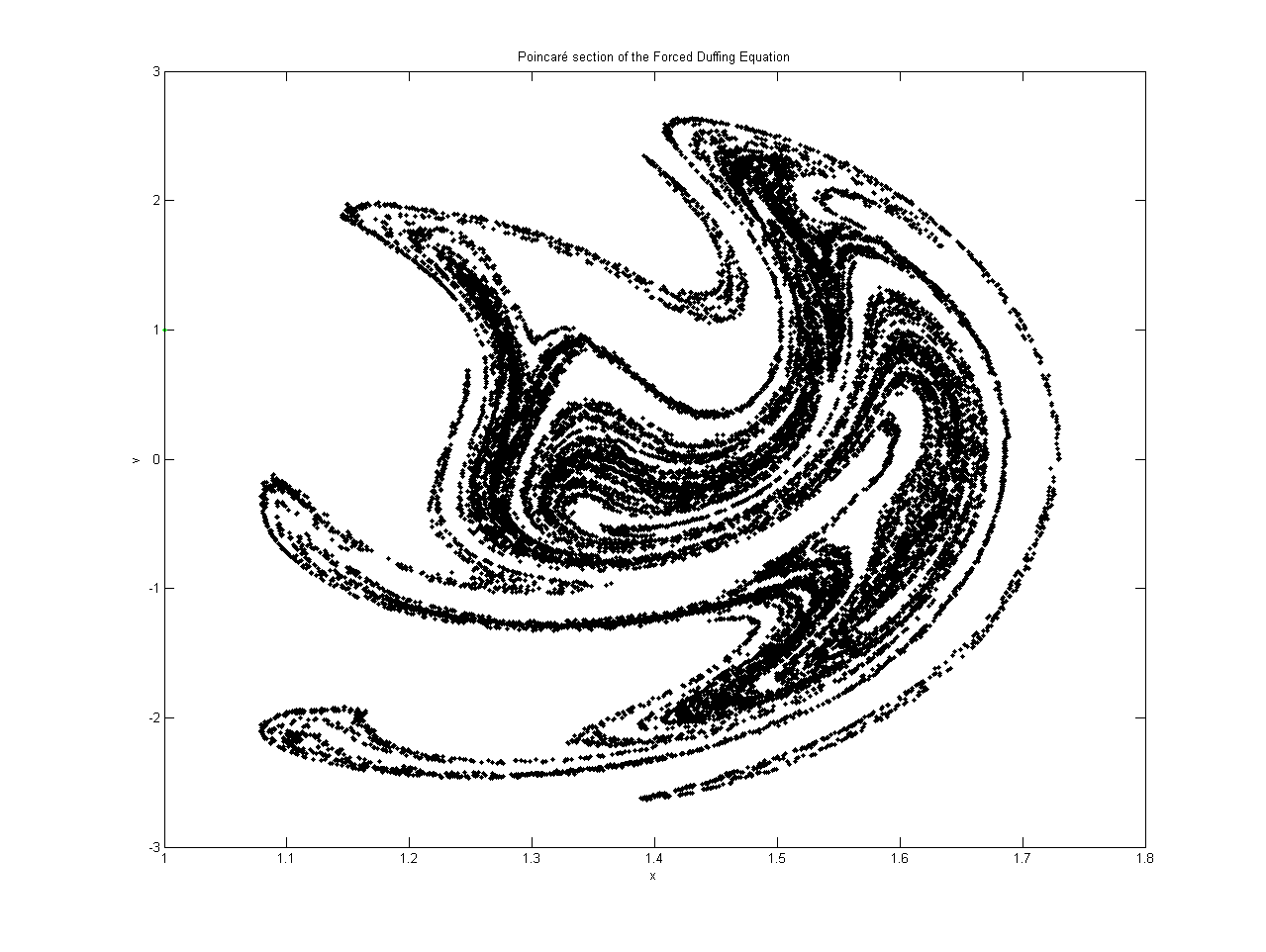 |
Poincaré Map
In mathematics, particularly in dynamical systems, a first recurrence map or Poincaré map, named after Henri Poincaré, is the intersection of a periodic orbit in the state space of a continuous dynamical system with a certain lower-dimensional subspace, called the Poincaré section, transversal to the flow of the system. More precisely, one considers a periodic orbit with initial conditions within a section of the space, which leaves that section afterwards, and observes the point at which this orbit first returns to the section. One then creates a map to send the first point to the second, hence the name ''first recurrence map''. The transversality of the Poincaré section means that periodic orbits starting on the subspace flow through it and not parallel to it. A Poincaré map can be interpreted as a discrete dynamical system with a state space that is one dimension smaller than the original continuous dynamical system. Because it preserves many properties of periodic and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Providence, Rhode Island
Providence is the capital and most populous city of the U.S. state of Rhode Island. One of the oldest cities in New England, it was founded in 1636 by Roger Williams, a Reformed Baptist theologian and religious exile from the Massachusetts Bay Colony. He named the area in honor of "God's merciful Providence" which he believed was responsible for revealing such a haven for him and his followers. The city developed as a busy port as it is situated at the mouth of the Providence River in Providence County, at the head of Narragansett Bay. Providence was one of the first cities in the country to industrialize and became noted for its textile manufacturing and subsequent machine tool, jewelry, and silverware industries. Today, the city of Providence is home to eight hospitals and List of colleges and universities in Rhode Island#Institutions, eight institutions of higher learning which have shifted the city's economy into service industries, though it still retains some manufacturin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings, advocacy and other programs. The society is one of the four parts of the Joint Policy Board for Mathematics and a member of the Conference Board of the Mathematical Sciences. History The AMS was founded in 1888 as the New York Mathematical Society, the brainchild of Thomas Fiske, who was impressed by the London Mathematical Society on a visit to England. John Howard Van Amringe was the first president and Fiske became secretary. The society soon decided to publish a journal, but ran into some resistance, due to concerns about competing with the American Journal of Mathematics. The result was the '' Bulletin of the American Mathematical Society'', with Fiske as editor-in-chief. The de facto journal, as intended, was influential ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Bond Hardening
Bond hardening is a process of creating a new chemical bond by strong laser fields—an effect opposite to bond softening. However, it is not opposite in the sense that the bond becomes stronger, but in the sense that the molecule enters a state that is diametrically opposite to the bond-softened state. Such states require laser pulses of high intensity, in the range of 1013–1015 W/cm2, and they disappear once the pulse is gone. Theory Bond hardening and bond softening share the same theoretical basis, which is described under the latter entry. Briefly, the ground and the first excited energy curves of the H2+ ion are dressed in photons. The laser field perturbs the curves and turns their crossings into anticrossings. Bond softening occurs on the lower branches of the anticrossings and bond hardening happens if the molecule is excited to the upper branches – see Fig. 1. To trap the molecule in the bond-hardened state, the anticrossing gap cannot be too small or too large. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Bond Softening
Bond softening is an effect of reducing the strength of a chemical bond A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing o ... by strong laser fields. To make this effect significant, the strength of the electric field in the laser light has to be comparable with the electric field the bonding electron "feels" from the nuclei of the molecule. Such fields are typically in the range of 1–10 V/Å, which corresponds to laser intensities 1013–1015 W/cm2. Nowadays, these intensities are routinely achievable from table-top Ti:Sapphire lasers. Theory Theoretical description of bond softening can be traced back to early work on dissociation of diatomic molecules in intense laser fields. While the quantitative description of this process requires quantum mechanics, it can be understood qualit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Gravitational Field
In physics, a gravitational field is a model used to explain the influences that a massive body extends into the space around itself, producing a force on another massive body. Thus, a gravitational field is used to explain gravitational phenomena, and is measured in newtons per kilogram (N/kg). Equivalently, it is measured in meters per second squared (m/s2). In its original concept, gravity was a force between point masses. Following Isaac Newton, Pierre-Simon Laplace attempted to model gravity as some kind of radiation field or fluid, and since the 19th century, explanations for gravity have usually been taught in terms of a field model, rather than a point attraction. In a field model, rather than two particles attracting each other, the particles distort spacetime via their mass, and this distortion is what is perceived and measured as a "force". In such a model one states that matter moves in certain ways in response to the curvature of spacetime, and that th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Harmonic Oscillator
In classical mechanics, a harmonic oscillator is a system that, when displaced from its Mechanical equilibrium, equilibrium position, experiences a restoring force ''F'' Proportionality (mathematics), proportional to the displacement ''x'': \vec F = -k \vec x, where ''k'' is a positive coefficient, constant. If ''F'' is the only force acting on the system, the system is called a simple harmonic oscillator, and it undergoes simple harmonic motion: sinusoidal oscillations about the equilibrium point, with a constant amplitude and a constant frequency (which does not depend on the amplitude). If a frictional force (Damping ratio, damping) proportional to the velocity is also present, the harmonic oscillator is described as a damped oscillator. Depending on the friction coefficient, the system can: * Oscillate with a frequency lower than in the Damping ratio, undamped case, and an amplitude decreasing with time (Damping ratio, underdamped oscillator). * Decay to the equilibrium p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width of Australia). The Moon is a planetary-mass object with a differentiated rocky body, making it a satellite planet under the geophysical definitions of the term and larger than all known dwarf planets of the Solar System. It lacks any significant atmosphere, hydrosphere, or magnetic field. Its surface gravity is about one-sixth of Earth's at , with Jupiter's moon Io being the only satellite in the Solar System known to have a higher surface gravity and density. The Moon orbits Earth at an average distance of , or about 30 times Earth's diameter. Its gravitational influence is the main driver of Earth's tides and very slowly lengthens Earth's day. The Moon's orbit around Earth has a sidereal period of 27.3 days. During each s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
George William Hill
George William Hill (March 3, 1838 – April 16, 1914) was an American astronomer and mathematician. Working independently and largely in isolation from the wider scientific community, he made major contributions to celestial mechanics and to the theory of ordinary differential equations. The importance of his work was explicitly acknowledged by Henri Poincaré in 1905. In 1909 Hill was awarded the Royal Society's Copley Medal, "on the ground of his researches in mathematical astronomy". Today, he is chiefly remembered for the Hill differential equation. Early life and education Hill was born in New York City to painter and engraver John William Hill and his wife, Catherine Smith. He moved to West Nyack with his family when he was eight years old. After high school, Hill attended Rutgers College, where he became interested in mathematics. At Rutgers, Hill came under the influence of professor Theodore Strong, who was a friend of pioneering US mathematician and astro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Hill Differential Equation
In mathematics, the Hill equation or Hill differential equation is the second-order linear ordinary differential equation : \frac + f(t) y = 0, where f(t) is a periodic function by minimal period \pi . By these we mean that for all t :f(t+\pi)=f(t), and :\int_0^\pi f(t) \,dt=0, and if p is a number with 0 < p < \pi , the equation must fail for some . It is named after , who introduced it in 1886. Because has period , the Hill equation can be rewritten using the of : : [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
|
Dynamical Systems
In mathematics, a dynamical system is a system in which a function describes the time dependence of a point in an ambient space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, the random motion of particles in the air, and the number of fish each springtime in a lake. The most general definition unifies several concepts in mathematics such as ordinary differential equations and ergodic theory by allowing different choices of the space and how time is measured. Time can be measured by integers, by real or complex numbers or can be a more general algebraic object, losing the memory of its physical origin, and the space may be a manifold or simply a set, without the need of a smooth space-time structure defined on it. At any given time, a dynamical system has a state representing a point in an appropriate state space. This state is often given by a tuple of real numbers or by a vector in a geometr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |