Jaccard Index

The Jaccard index, also known as the Jaccard similarity coefficient, is a statistic used for gauging the similarity and diversity of sample sets. It was developed by Grove Karl Gilbert in 1884 as his ratio of verification (v) and now is frequently referred to as the Critical Success Index in meteorology. It was later developed independently by Paul Jaccard, originally giving the French name ''coefficient de communauté'', and independently formulated again by T. Tanimoto. Thus, the Tanimoto index or Tanimoto coefficient are also used in some fields. However, they are identical in generally taking the ratio of Intersection over Union. The Jaccard coefficient measures similarity between finite sample sets, and is defined as the size of the intersection divided by the size of the union of the sample sets:

:$J(A,B) = = .$

Note that by design, $0\le J(A,B)\le 1.$ If ''A'' intersection ''B'' is empty, then ''J''(''A'',''B'') = 0. The Jaccard coefficient is widely used in computer science, ecology, genomics, and other sciences, where binary or binarized data are used. Both the exact solution and approximation methods are available for hypothesis testing with the Jaccard coefficient.

Jaccard similarity also applies to bags, i.e., Multisets. This has a similar formula, but the symbols mean
bag intersection and bag sum (not union). The maximum value is 1/2.
:$J(A,B) = = .$

The Jaccard distance, which measures ''dis''similarity between sample sets, is complementary to the Jaccard coefficient and is obtained by subtracting the Jaccard coefficient from 1, or, equivalently, by dividing the difference of the sizes of the union and the intersection of two sets by the size of the union:

:$d_J(A,B) = 1 - J(A,B) = .$

An alternative interpretation of the Jaccard distance is as the ratio of the size of the symmetric difference $A \triangle B = (A \cup B) - (A \cap B)$ to the union.
Jaccard distance is commonly used to calculate an ''n'' × ''n'' matrix for clustering and multidimensional scaling of ''n'' sample sets.

This distance is a metric on the collection of all finite sets.

There is also a version of the Jaccard distance for measures, including probability measures. If $\mu$ is a measure on a measurable space $X$, then we define the Jaccard coefficient by

:$J_\mu(A,B) = ,$

and the Jaccard distance by

:$d_\mu(A,B) = 1 - J_\mu(A,B) = .$

Care must be taken if $\mu(A \cup B) = 0$ or $\infty$, since these formulas are not well defined in these cases.

The MinHash min-wise independent permutations locality sensitive hashing scheme may be used to efficiently compute an accurate estimate of the Jaccard similarity coefficient of pairs of sets, where each set is represented by a constant-sized signature derived from the minimum values of a hash function.

Similarity of asymmetric binary attributes

Given two objects, ''A'' and ''B'', each with ''n'' binary attributes, the Jaccard coefficient is a useful measure of the overlap that ''A'' and ''B'' share with their attributes. Each attribute of ''A'' and ''B'' can either be 0 or 1. The total number of each combination of attributes for both ''A'' and ''B'' are specified as follows:

:$M_$ represents the total number of attributes where ''A'' and ''B'' both have a value of 1.
:$M_$ represents the total number of attributes where the attribute of ''A'' is 0 and the attribute of ''B'' is 1.
:$M_$ represents the total number of attributes where the attribute of ''A'' is 1 and the attribute of ''B'' is 0.
:$M_$ represents the total number of attributes where ''A'' and ''B'' both have a value of 0.

Each attribute must fall into one of these four categories, meaning that
:$M_ + M_ + M_ + M_ = n.$

The Jaccard similarity coefficient, ''J'', is given as
:$J = .$

The Jaccard distance, ''d''_''J'', is given as
:$d_J = = 1 - J.$

Statistical inference can be made based on the Jaccard similarity coefficients, and consequently related metrics. Given two sample sets ''A'' and ''B'' with ''n'' attributes, a statistical test can be conducted to see if an overlap is statistically significant. The exact solution is available, although computation can be costly as ''n'' increases. Estimation methods are available either by approximating a multinomial distribution or by bootstrapping.

Difference with the simple matching coefficient (SMC)

When used for binary attributes, the Jaccard index is very similar to the simple matching coefficient. The main difference is that the SMC has the term $M_$ in its numerator and denominator, whereas the Jaccard index does not. Thus, the SMC counts both mutual presences (when an attribute is present in both sets) and mutual absence (when an attribute is absent in both sets) as matches and compares it to the total number of attributes in the universe, whereas the Jaccard index only counts mutual presence as matches and compares it to the number of attributes that have been chosen by at least one of the two sets.

In market basket analysis, for example, the basket of two consumers who we wish to compare might only contain a small fraction of all the available products in the store, so the SMC will usually return very high values of similarities even when the baskets bear very little resemblance, thus making the Jaccard index a more appropriate measure of similarity in that context. For example, consider a supermarket with 1000 products and two customers. The basket of the first customer contains salt and pepper and the basket of the second contains salt and sugar. In this scenario, the similarity between the two baskets as measured by the Jaccard index would be 1/3, but the similarity becomes 0.998 using the SMC.

In other contexts, where 0 and 1 carry equivalent information (symmetry), the SMC is a better measure of similarity. For example, vectors of demographic variables stored in dummy variables, such as gender, would be better compared with the SMC than with the Jaccard index since the impact of gender on similarity should be equal, independently of whether male is defined as a 0 and female as a 1 or the other way around. However, when we have symmetric dummy variables, one could replicate the behaviour of the SMC by splitting the dummies into two binary attributes (in this case, male and female), thus transforming them into asymmetric attributes, allowing the use of the Jaccard index without introducing any bias. The SMC remains, however, more computationally efficient in the case of symmetric dummy variables since it does not require adding extra dimensions.

Weighted Jaccard similarity and distance

If $\mathbf = (x_1, x_2, \ldots, x_n)$ and $\mathbf = (y_1, y_2, \ldots, y_n)$ are two vectors with all real $x_i, y_i \geq 0$, then their Jaccard similarity coefficient (also known then as Ruzicka similarity) is defined as

:$J_\mathcal(\mathbf, \mathbf) = \frac,$

and Jaccard distance (also known then as Soergel distance)

:$d_(\mathbf, \mathbf) = 1 - J_\mathcal(\mathbf, \mathbf).$

With even more generality, if $f$ and $g$ are two non-negative measurable functions on a measurable space $X$ with measure $\mu$, then we can define

:$J_\mathcal(f, g) = \frac,$

where $\max$ and $\min$ are pointwise operators. Then Jaccard distance is

:$d_(f, g) = 1 - J_\mathcal(f, g).$

Then, for example, for two measurable sets $A, B \subseteq X$, we have $J_\mu(A,B) = J(\chi_A, \chi_B),$ where $\chi_A$ and $\chi_B$ are the characteristic functions of the corresponding set.

Probability Jaccard similarity and distance

The weighted Jaccard similarity described above generalizes the Jaccard Index to positive vectors, where a set corresponds to a binary vector given by the indicator function, i.e. $x_i \in \$. However, it does not generalize the Jaccard Index to probability distributions, where a set corresponds to a uniform probability distribution, i.e.

:$x_i = \begin \frac & i \in X \\ 0 & \text \end$

It is always less if the sets differ in size. If $, X, > , Y,$, and $x_i = \mathbf_X(i)/, X, , y_i = \mathbf_Y(i)/, Y,$ then

:$J_\mathcal(x,y) = \frac < J(X,Y).$

Instead, a generalization that is continuous between probability distributions and their corresponding support sets is

:$J_\mathcal(x,y) = \sum_ \frac$

which is called the "Probability" Jaccard. It has the following bounds against the Weighted Jaccard on probability vectors.

:$J_\mathcal(x,y) \leq J_\mathcal(x,y) \leq \frac$

Here the upper bound is the (weighted) Sørensen–Dice coefficient.
The corresponding distance, $1 - J_\mathcal(x,y)$, is a metric over probability distributions, and a pseudo-metric over non-negative vectors.

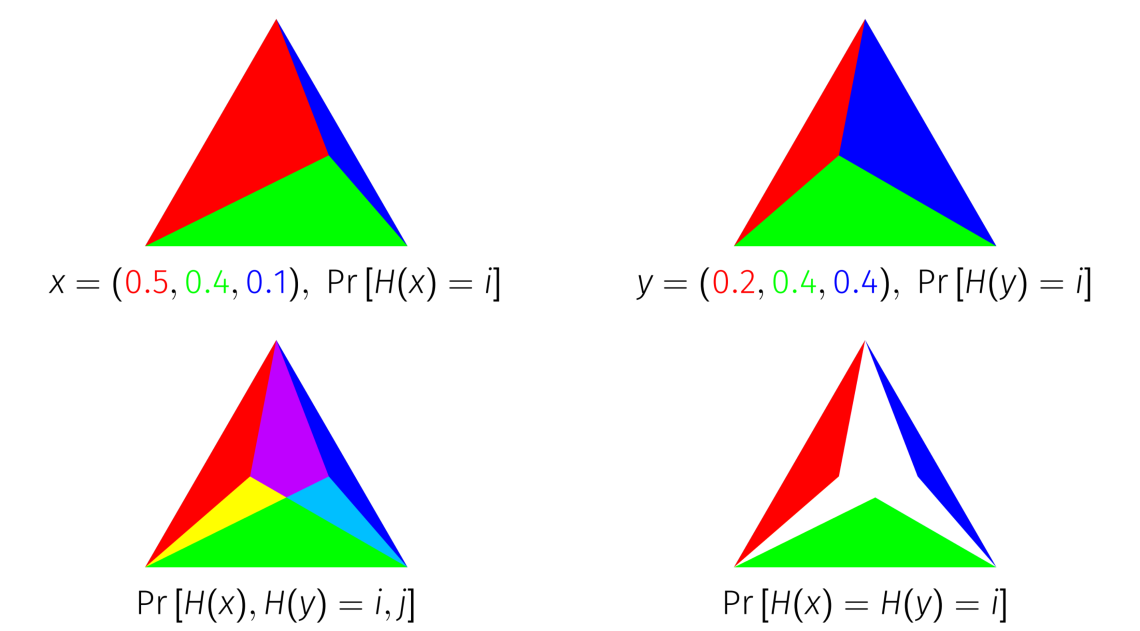
The Probability Jaccard Index has a geometric interpretation as the area of an intersection of simplices. Every point on a unit $k$-simplex corresponds to a probability distribution on $k+1$ elements, because the unit $k$-simplex is the set of points in $k+1$ dimensions that sum to 1. To derive the Probability Jaccard Index geometrically, represent a probability distribution as the unit simplex divided into sub simplices according to the mass of each item. If you overlay two distributions represented in this way on top of each other, and intersect the simplices corresponding to each item, the area that remains is equal to the Probability Jaccard Index of the distributions.

Optimality of the Probability Jaccard Index

Consider the problem of constructing random variables such that they collide with each other as much as possible. That is, if $X\sim x$ and $Y\sim y$, we would like to construct $X$ and $Y$ to maximize \Pr =Y/math>. If we look at just two distributions $x,y$ in isolation, the highest \Pr =Y/math> we can achieve is given by $1 - \text(x,y)$ where $\text$ is the Total Variation distance. However, suppose we weren't just concerned with maximizing that particular pair, suppose we would like to maximize the collision probability of any arbitrary pair. One could construct an infinite number of random variables one for each distribution $x$, and seek to maximize \Pr =Y/math> for all pairs $x,y$. In a fairly strong sense described below, the Probability Jaccard Index is an optimal way to align these random variables.

For any sampling method $G$ and discrete distributions $x,y$, if \Pr (x) = G(y)> J_\mathcal(x,y) then for some $z$ where $J_\mathcal(x,z)>J_\mathcal(x,y)$ and $J_\mathcal(y,z)>J_\mathcal(x,y)$, either \Pr (x) = G(z)< J_\mathcal(x,z) or \Pr (y) = G(z)< J_\mathcal(y,z).

That is, no sampling method can achieve more collisions than $J_\mathcal$ on one pair without achieving fewer collisions than $J_\mathcal$ on another pair, where the reduced pair is more similar under $J_\mathcal$ than the increased pair. This theorem is true for the Jaccard Index of sets (if interpreted as uniform distributions) and the probability Jaccard, but not of the weighted Jaccard. (The theorem uses the word "sampling method" to describe a joint distribution over all distributions on a space, because it derives from the use of weighted minhashing algorithms that achieve this as their collision probability.)

This theorem has a visual proof on three element distributions using the simplex representation.

Tanimoto similarity and distance

Various forms of functions described as Tanimoto similarity and Tanimoto distance occur in the literature and on the Internet. Most of these are synonyms for Jaccard similarity and Jaccard distance, but some are mathematically different. Many sources cite an IBM Technical Report as the seminal reference. The report is available fro
several libraries

In "A Computer Program for Classifying Plants", published in October 1960, a method of classification based on a similarity ratio, and a derived distance function, is given. It seems that this is the most authoritative source for the meaning of the terms "Tanimoto similarity" and "Tanimoto Distance". The similarity ratio is equivalent to Jaccard similarity, but the distance function is ''not'' the same as Jaccard distance.

Tanimoto's definitions of similarity and distance

In that paper, a "similarity ratio" is given over bitmaps, where each bit of a fixed-size array represents the presence or absence of a characteristic in the plant being modelled. The definition of the ratio is the number of common bits, divided by the number of bits set (''i.e.'' nonzero) in either sample.

Presented in mathematical terms, if samples ''X'' and ''Y'' are bitmaps, $X_i$ is the ''i''th bit of ''X'', and $\land , \lor$ are bitwise ''and'', '' or'' operators respectively, then the similarity ratio $T_s$ is

: $T_s(X,Y) = \frac$

If each sample is modelled instead as a set of attributes, this value is equal to the Jaccard coefficient of the two sets. Jaccard is not cited in the paper, and it seems likely that the authors were not aware of it.

Tanimoto goes on to define a "distance coefficient" based on this ratio, defined for bitmaps with non-zero similarity:

: $T_d(X,Y) = -\log_2 ( T_s(X,Y) )$

This coefficient is, deliberately, not a distance metric. It is chosen to allow the possibility of two specimens, which are quite different from each other, to both be similar to a third. It is easy to construct an example which disproves the property of triangle inequality.

Other definitions of Tanimoto distance

Tanimoto distance is often referred to, erroneously, as a synonym for Jaccard distance $1-T_s$. This function is a proper distance metric. "Tanimoto Distance" is often stated as being a proper distance metric, probably because of its confusion with Jaccard distance.

If Jaccard or Tanimoto similarity is expressed over a bit vector, then it can be written as

: $f(A,B) =\frac$

where the same calculation is expressed in terms of vector scalar product and magnitude. This representation relies on the fact that, for a bit vector (where the value of each dimension is either 0 or 1) then

:$A \cdot B = \sum_i A_iB_i = \sum_i ( A_i \land B_i)$

and

:$\, A\, ^2 = \sum_i A_i^2 = \sum_i A_i.$

This is a potentially confusing representation, because the function as expressed over vectors is more general, unless its domain is explicitly restricted. Properties of $T_s$ do not necessarily extend to $f$. In particular, the difference function $1-f$ does not preserve triangle inequality, and is not therefore a proper distance metric, whereas $1 - T_s$ is.

There is a real danger that the combination of "Tanimoto Distance" being defined using this formula, along with the statement "Tanimoto Distance is a proper distance metric" will lead to the false conclusion that the function $1-f$ is in fact a distance metric over vectors or multisets in general, whereas its use in similarity search or clustering algorithms may fail to produce correct results.

Lipkus uses a definition of Tanimoto similarity which is equivalent to $f$, and refers to Tanimoto distance as the function $1-f$. It is, however, made clear within the paper that the context is restricted by the use of a (positive) weighting vector $W$ such that, for any vector ''A'' being considered, $A_i \in \.$ Under these circumstances, the function is a proper distance metric, and so a set of vectors governed by such a weighting vector forms a metric space under this function.

Jaccard index in binary classification confusion matrices

In confusion matrices employed for binary classification, the Jaccard index can be framed in the following formula:

:$\text = \frac$

where TP are the true positives, FP the false positives and FN the false negatives.

See also

* Overlap coefficient
* Simple matching coefficient
* Hamming distance
* Sørensen–Dice coefficient, which is equivalent: $J=S/(2-S)$ and $S=2J/(1+J)$ ($J$: Jaccard index, $S$: Sørensen–Dice coefficient)
* Tversky index
* Correlation
* Mutual information, a normalized metricated variant of which is an entropic Jaccard distance.

References

Further reading

*
*
*

External links

Introduction to Data Mining lecture notes from Tan, Steinbach, Kumar

SimMetrics a sourceforge implementation of Jaccard index and many other similarity metrics

A web-based calculator for finding the Jaccard Coefficient



Intersection over Union (IoU) for object detection

Kaggle Dstl Satellite Imagery Feature Detection - Evaluation

Similarity and dissimilarity measures used in data science

{{DEFAULTSORT:Jaccard Index
Index numbers
Measure theory
Clustering criteria
String metrics
Similarity measures